定数截尾场合下三参数陈氏分布的位置参数估计★

林冰钰，顾蓓青，徐晓岭

（上海对外经贸大学统计与信息学院，上海 201620）

0 引言

基于某些产品具有浴盆状的失效率函数，Chen Zhenmin[1]提出了一个新的两参数寿命分布，记为陈氏分布，其分布函数如下：

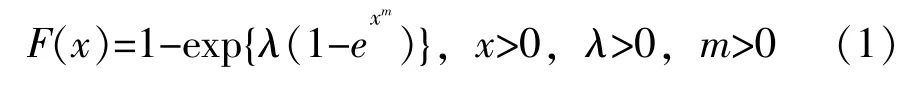
当m<1时，失效率函数呈现浴盆状；当m≥1时，失效率函数为单调递增函数。基于上述的陈氏分布，后来的学者做了很多的研究。Wu J W等[2]基于II型截尾样本，提出了陈氏分布参数的不同类型的精确置信区间和精确联合置信区间。王炳兴[3]基于II型截尾样本，讨论了陈氏分布的逆矩估计和置信区间。Shuo-Jye[4]研究了陈氏分布的渐进II型截尾样本的最大似然估计。Sarhan A M等[5]讨论了陈氏分布的两个未知参数的极大似然估计和贝叶斯估计。Selim M A[6]讨论了陈氏分布未知参数的贝叶斯和非贝叶斯估计问题。Javadkhani N等[7]提出了不同的贝叶斯估计方法，估计陈氏分布的参数和可靠性函数。Sarhan A M等[8]基于陈氏分布，使用最大似然方法和贝叶斯方法对二类删失数据和渐进二类删失数据进行推断。Khan M S等[9]基于指数-陈氏分布的一个推广，得到了参数的最大似然估计。Tarvirdizade B等[10]介绍了一种由威布尔分布和陈氏分布复合而成的寿命分布，它具有递增、递减和浴盆形的失效率函数。Yousaf F等[11]研究了基于贝叶斯方法，两参数陈氏分布在不同情况下的参数估计。Kayal T等[12]基于渐进首次失效删失的两参数陈氏分布的估计和预测，得到了参数的经典估计。

为了让具有“浴盆状”失效率函数的陈氏分布具有更强的灵活性，可以更好地拟合实际的寿命数据，Xie M等[13]针对陈氏分布进行了进一步的研究，在该分布的基础上增加一个刻度参数，提出了改进的陈氏分布，其分布函数为：

将参数作适当变换，可得到如下形式的分布函数：

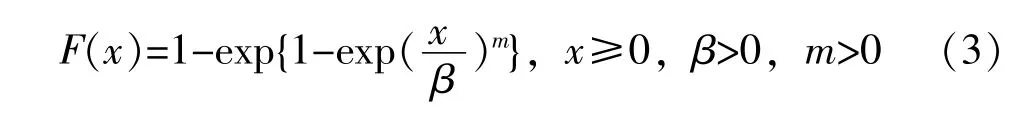
若在上述分布函数的基础上引入位置参数μ，则可得到如下分布函数：

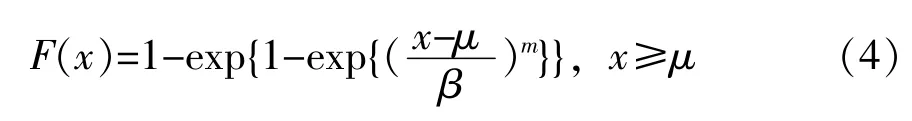
记为三参数陈氏分布，其中位置参数为μ>0，尺度参数为m>0，形状参数为β>0。

1 位置参数μ的点估计

假设总体X服从三参数陈氏分布，现假定有n个寿命服从三参数陈氏分布的产品进行定数截尾试验，到有r个产品失效时停止试验，得到试验的第1到第r个次序统计量为：X（1）≤X（2）≤…X（r），1≤r≤n其对应第1到第r个次序观测值为：x（1）≤x（2）≤…x（r）。

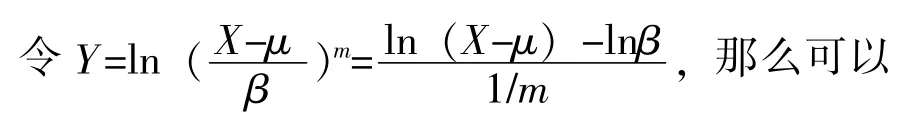
易知，G（μ）是一个枢轴量。考虑不同样本容量和不同截尾数，进行10 000次的Monte-Carlo模拟得到枢轴量G（μ）的上侧分位数表、期望和方差汇总至表1，因篇幅有限，只列了部分情况，其中r=n即为全样本场合。

表1 枢轴量G(μ)的上侧分位数表

为了得到位置参数μ的点估计，构建如下矩方程：

表2 G（μ）的期望满足E[G（μ）]≤lim μ→0+G（μ）的次数k1 m β μ=0.5 μ=1 μ=1.5 μ=3 r1 r2 r3 r1 r2 r3 r1 r2 r3 r1 r2 r3 0.5 0.5 1 000 1 000 1 000 1 000 1 000 1 000 1 000 1 000 1 000 1 000 1 000 1 000 1 999 999 1 000 1 000 998 1 000 1 000 1 000 1 000 1 000 1 000 1 000 1.5 986 987 972 993 991 987 995 997 986 999 999 997 3 755 724 724 790 797 775 827 790 808 863 839 840 1 0.5 1 000 1 000 1 000 1 000 1 000 1 000 1 000 1 000 1 000 1 000 1 000 1 000 1 998 1 000 999 1 000 1 000 1 000 1 000 1 000 1 000 1 000 1 000 1 000 1.5 947 943 933 980 977 978 990 986 982 998 997 992 3 644 629 635 714 695 704 770 743 748 823 810 791 1.5 0.5 1 000 1 000 1 000 1 000 1 000 1 000 1 000 1 000 1 000 1 000 1 000 1 000 1 993 997 996 1 000 1 000 996 1 000 999 1 000 1 000 1 000 1 000 1.5 889 895 901 967 966 959 983 979 972 990 997 993 3 585 595 592 684 664 657 725 729 681 794 788 783 3 0.5 1 000 1 000 1 000 1 000 1 000 1 000 1 000 1 000 1 000 1 000 1 000 1 000 1 972 975 965 997 993 994 1 000 998 994 1 000 999 1 000 1.5 781 794 787 905 904 889 938 932 938 984 972 979 3 550 539 508 595 606 599 632 637 627 720 716 730

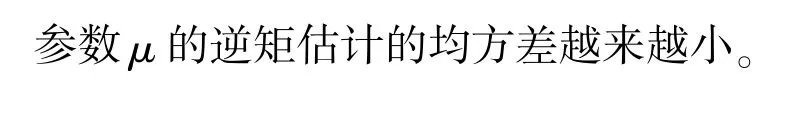
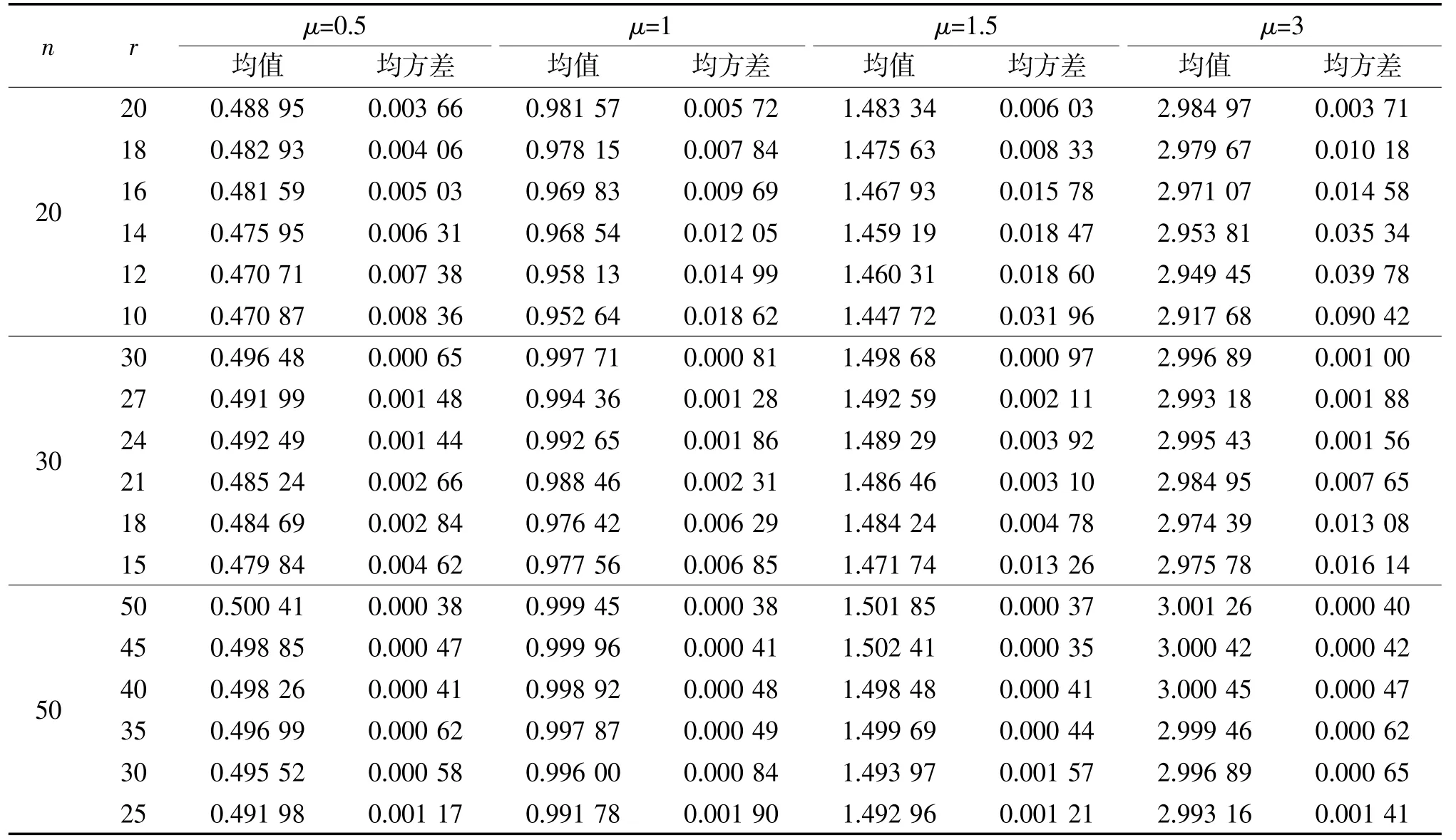
表3 位置参数的逆矩估计模拟结果

2 位置参数μ的置信下限

为了考察位置参数μ置信下限的精度，取不同的样本容量和定数截尾数，参数真值为μ=0.5，1，1.5，3，β=1， m=0.5，进 行1 000次Monte-Carlo模拟产生来自三参数陈氏分布的简单随机样本，在置信水平为1-α=95%下，得到参数μ的置信下限μL的均值，并记录真值大于置信下限的次数，结果如表5所示。从中可以得到：1）全样本场合下，随着样本容量n的增加，位置参数μ的平均置信下限呈增加趋势；2）置信下限小于真值的次数在950次附近，也就是说基本上达到了95%的置信水平。

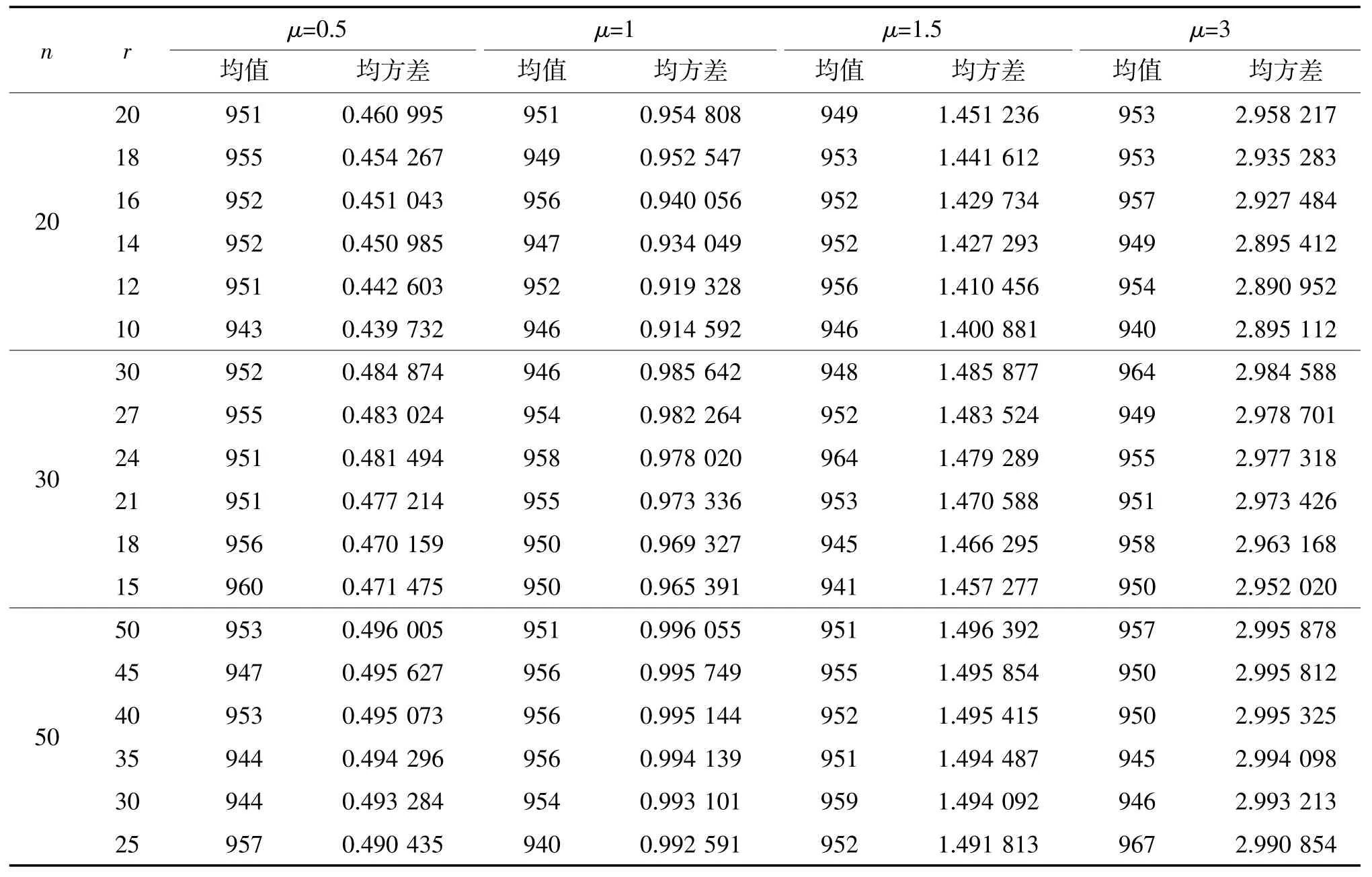
表5 位置参数μ的置信下限模拟结果(置信水平1-α=0.95)

3 模拟算例分析

a）例1

取样本容量n=3，参数真值μ=3，β=3，m=0.8。通过Monte-Carlo数据模拟产生来自三参数陈氏分布的一个次序样本数据，如下：

表4 分位数gα满足gα≤lim μ→0+G（μ）的次数k2

由本文的方法，可以计算得到在不同的截尾情况下，位置参数的逆矩估计和置信水平95%下的置信下限，如表6所示。

表6 例1的计算结果

b）例2

取样本容量n=50，参数真值μ=3，β=3，m=1。通过Monte-Carlo数据模拟产生来自三参数陈氏分布的一个次序样本数据，如下：

3.051 39，3.081 73，3.126 38，3.173 24，3.226 49，3.232 90，3.262 68，3.531 94，3.544 40，3.601 35，3.655 54，3.662 05，3.842 02，3.842 93，3.859 39，3.890 68，3.967 87，4.059 71，4.083 28，4.267 77，4.299 73，4.352 58，4.428 30，4.745 93，4.974 10，5.023 16，5.049 66，5.175 57，5.191 01，5.273 74，5.386 03，5.411 33，5.426 53，5.442 65，5.605 22，5.632 36，5.725 40，5.860 05，5.870 92，5.917 37，5.996 87，6.086 26，6.155 46，6.174 43，6.181 56，6.233 87，6.429 36，6.674 60，6.782 45，9.189 59

由本文的方法，可以计算得到在不同的截尾情况下，位置参数的逆矩估计和置信水平95%下的置信下限，如表7所示。

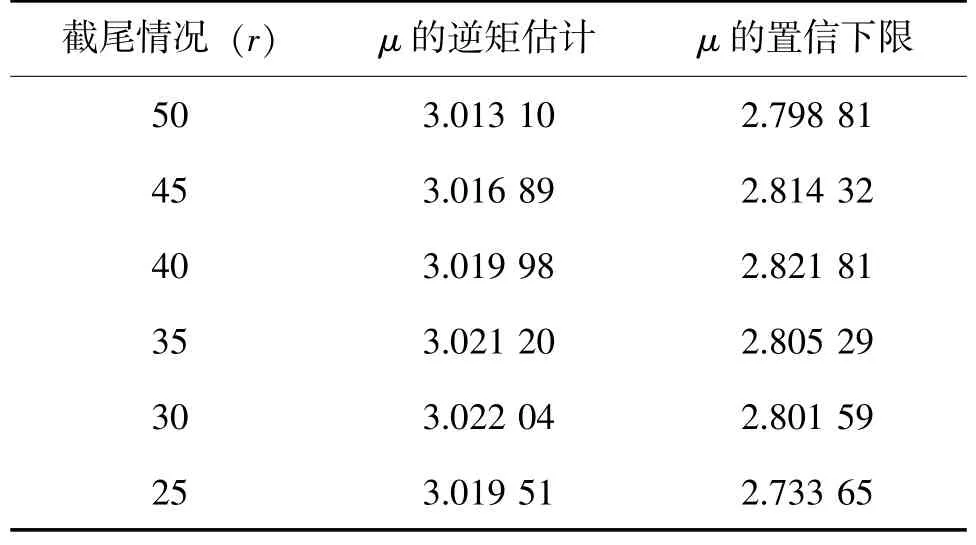
表7 例2的计算结果

4 结束语

本文基于两参数陈氏分布引入了一个位置参数，得到三参数陈氏分布。考虑在定数截尾数据场合下位置参数的点估计和置信下限，通过构造一个枢轴量，得到其在不同样本容量和截尾数下的分位数和期望，由此得到位置参数的逆矩估计和置信下限，并通过Monte-Carlo模拟考察了位置参数的估计精度。