Effect of void size and Mg contents on plastic deformation behaviors of Al–Mg alloy with pre-existing void: Molecular dynamics study

Ning Wei(魏宁) Ai-Qiang Shi(史爱强) Zhi-Hui Li(李志辉)Bing-Xian Ou(区炳显) Si-Han Zhao(赵思涵) and Jun-Hua Zhao(赵军华)

1Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment and Technology,Jiangnan University,Wuxi 214122,China

2China Aerodynamics Research and Development Center,Mianyang 621000,China

3National Laboratory for Computational Fluid Dynamics,Beijing 100191,China

4National Graphene Products Quality Supervision and Inspection Center,

Keywords: Al–Mg alloys,molecular dynamics,nanovoid,plastic deformation

1. Introduction

Al–Mg alloys exhibit excellent specific strength, corrosion resistance and fatigue resistance, which is widely used in aviation,[1,2]lightweight automotive,[3,4]marine[5,6]and defense fields. However, micro defects such as voids and cracks are generated inevitably during the process of materials formation.[7–9]Irradiation damage also causes voids easily in metals and alloys.[10]Numerous experimental studies[11–13]have found that the growth and coalescence of the voids inside Al alloys are the main reasons for fracture. As crucial engineering materials,the mechanical properties of Al–Mg alloys have been affected by voids extensively.With decreasing sizes of materials, the effect of voids becomes more significant.For example, the failure of the Al-or Cu-based films used as radiation tolerant media brings about a significant reliability concern in microelectronic devices.[14]Hence, it is of great significance to study the evolution of voids in metal materials for better understanding the plastic deformation of metals and to improve the reliability of microelectronic devices.[15]Although the process of void growth and coalescence can be observed byin situtransmission electron microscopy(TEM),it is inconvenient to explore the dynamic mechanism of void evolution completely, such as dislocation nucleation, phase transition and dislocation slippage. Meanwhile,as the size of voids is close to nanoscale, the finite element method to capture the dislocation emission and phase transition during the void growth becomes challenging severely.[16]Alternatively,molecular dynamics(MD)based on a reliable empirical interaction potential enables detailed understanding of microscopic defects at the atomic scale,building a foundation to study the deformation mechanism of nano void.

In recent years, extensive research using MD simulations has been conducted to probe mechanical behaviors of nanoporous materials and the effect of voids.[17–19]Shanget al.investigated the size-dependent effect of pre-void in the Ni/Ni3Al interface on tensile strength,and found that the small void disperses the local energy caused by lattice misfit at the interface, generating higher yield stress than the defect-free structure.[20]Guanet al.simulated the dynamic response of Al containing spherical void under different loading patterns.The results show that the response of the sample is slightly dependent on the loading patterns under weak loadings.[21]Xinet al.reported spinodal strengthened ultralightweight Mg–Al alloys with specific yield strengths surpassing almost every other engineering alloy, and revealed that the lattice mismatch at the diffuse transition region between the spinodal zones and matrix is the dominating factor for ultrahigh specific strength using the computational simulations.[22]Jinget al.reported evolution mechanism of a spherical void in polycrystalline copper under uniaxial tensile loading, proposing a criterion that there exists a critical void diameter dependent on grain size.[23]Moreover,the interaction between grain boundary and void in twin-crystal copper depending on temperature is reported.[24]The dynamic damage behaviors of single crystal HCP-Zr are examined,and the results reveal that the preference of void nucleation and phase transition is dominated by temperature and strain rate.[25]The effect of hard phase Ti and soft phase Mg nanoclusters in Al matrix on the tensile strength of materials is investigated.[26]Effect of layer thickness and strain rate on mechanical properties of Ti/Ni multilayered nanowires is reported.[27]Bahramyanet al.simulated the interaction between edge dislocation and void in pure Al and Al–Mg alloys.[28]Moreover,void growth in high entropy alloys has also been studied.[29,30]

Mg is the primary alloying element of Al alloys. Although the mechanical behaviors of Al–Mg alloys have been extensively reported,a systematical study on the plastic deformation mechanism of pre-void Al–Mg alloys is still lacking.In this paper, MD simulations are utilized to analyze the influences of Mg content,void size and temperature on the void evolution and tensile strength of Al–Mg alloys. These results may have significant implications for understanding the plastic deformation mechanism of voids in Al–Mg or other alloys.

2. Model and simulation method

The desired Al–Mg alloys are constructed by replacing a selected percentage of Al atoms with the same ratio of Mg atoms at the same locations,[31,32]as shown in Fig.2(a). The initial size of the simulation box is approximately 2.4×16.2×20.2 nm3and the orientations of [100], [010], and [001] are taken inx,y, andzdirections, respectively. After the defectfree samples are established,a circular void is introduced into the center of the samples by deleting atoms. The embedded atom method (EAM) interatomic potential developed by Liuet al.[33]is used to described Al–Al, Al–Mg and Mg–Mg interactions in our simulations, which has been proven to predict the mechanical properties of Al–Mg alloys[26,34]in recent years with high accuracy. In this work, MD simulations are carried out using the large-scale atomic/molecular massively parallel simulator(LAMMPS).[35]

Periodic boundary conditions are applied in all threedimensional directions. Before the relaxation and tensile simulation, all samples are accomplished by adjusting the atom coordinates for energy minimization, where force and energy tolerances are 10-12. Then, the models are conducted to relaxation(60 ps)using NPT ensemble(Nose/Hoover isobaricisothermal ensemble) at 300 K and 0 bar with time steps of 0.001 ps. The structures are optimized when the system potential energy converges. Subsequently, the uniaxial tensile loading is carried out (z-axis) with a constant strain rate of 0.001 ps-1, which is a typical value in MD simulations. Thexandydimensions remain unchanged to deform freely and maintain the stress near 1 atm in these two directions. Meanwhile,the temperature is maintained at 300 K by rescaling the velocities of the atoms explicitly during the tensile process.After the tensile simulations, the methods of dislocation extraction algorithm (DXA)[36]and construct surface mesh[37]of the open visualization tool (OVITO)[38]are utilized to reveal and analyze the variation of dislocation and void volume.

To verify the reliability of the calculation results,the simulations on the defect-free pure Al models are carried out firstly, and the results are shown in Table 1. Young’s modulus is obtained by linear fitting of the stress–strain curve in the elastic stage.[39]The results are well consistent with the literature.[40]Due to the difference of the potentials used,the results using potential developed by Liuet al.[33]are slightly lower than those in the literature,[40]and Young’s modulus is consistent with the experiment.[41]

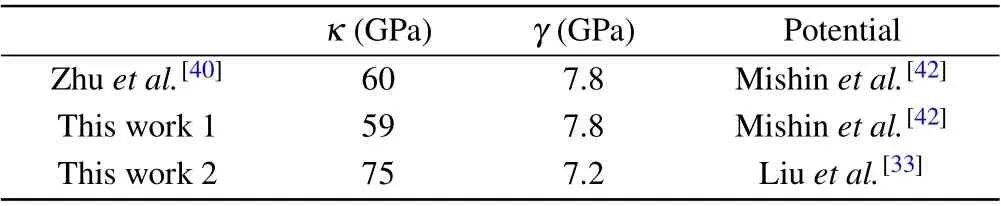
κ (GPa) γ (GPa) Potential Zhu et al.[40] 60 7.8 Mishin et al.[42]This work 1 59 7.8 Mishin et al.[42]This work 2 75 7.2 Liu et al.[33]

3. Results and discussion

3.1. Effect of Mg contents on mechanical properties

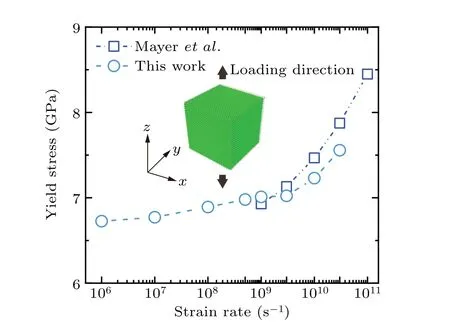
We first examine the strain rate effects on mechanical properties of pure Al. The yield stress is obtained with different loading strain rates ranging from 106s-1to 5×1010s-1,as shown in Fig.1. It shows that the yield stress increases with strain rate, which is consistent with that reported by Mayeret al.[43]and its trend becomes steep when strain rate is over 5×109s-1. The yield stress is added by 4.1%from strain rate of 106s-1to 109s-1. Considering the simulation consume,the strain rate of 109s-1is employed in the present study.

Mg content of Al–Mg alloys ranges from 2% to 5%,[44]and Fig.2(b)shows the typical stress–strain curves of the samples with void diameter 12 °A.To some extent,the stress–strain curve can reflect the overall mechanical properties of materials. As seen in Fig.2(b),the curves of all the samples show a linear increase in the initial stage of deformation and then enter the plastic stage.Here,the peak point of the stress–strain curve is defined as the yield stress. Figure 2(c)shows the yield stress and Young’s modulus of the samples with different Mg contents. As seen in the figure,the yield stress decreases slightly with Mg increased. These results agree well with those of Samiriet al.[45]and Kumaret al.[46]on the mechanical properties of Al–Mg alloys. The reason for the phenomenon opposite to macroscopic solid solution strengthening may be the transition from plastic deformation dominated by dislocation slippage at macroscopic quasi-static low strain rates to dislocation nucleation dominated failure mechanism at microscopic extreme high rates,[31]which was reported by Nitolet al.[31]In dislocation-starved nanoporous alloys,the distortion of the host lattice by solute atoms can retard dislocation glide, but aid dislocation nucleation. Compared with pure Al, the yield stress and Young’s modulus of Al-5%Mg alloy drop by 10.5%and 7%, respectively. It can be seen that the yield stress is more sensitive to Mg content than Young’s modulus.

To further verify the reliability of the simulation results.We choose the pure Al with void diameter 12 °A as the representative sample, as shown in the inset of Fig. 3(b), and calculate the stress componentσzof the atoms in various regions under uniaxial tension at 300 K. The stress–strain curves are obtained in Fig.3(a). Seen from Fig.3(b),y0is equal to 81 °A,ais void radius,andyiwithibeing the number of the atomic regions denotes the distance between the atoms in different regions and the center of the void,where yield stress is obtained when the strain of the curve is 8% in Fig. 3(a). According to the elastic theory, the stress componentσzofyi/y0can be derived using the existing Kirsch’s solution. In Fig. 3(b), the MD results are in good agreement with those of Eq.(1),where the yield stress decreases monotonically as risingyi/y0and approaches to a stable value of the far-field tensile stressq(q=5.98 GPa here). The reliability of the simulation results is verified.

In plastic deformation of the samples with defects, void fraction is of great importance, which can exhibit the severity of the deformation of the system. Shown in Fig. 4(a) is the void fraction of samples with different Mg as a function of strain. The process of void deformation can be divided into three stages. Similar results are observed in single crystal copper films containing elliptic voids studied by Suet al.[16]. In the first stage,the void fraction has no significant change and maintains the initial value in the elastic stage, where changes in the shapes of the voids are depicted in Fig.5(a). Compared to the voids withε=0%, shapes of the voids are basically unchanged atε=2%. As the loading progresses, the voids elongate slightly along the loading direction,taking on an elliptical shape. In the second stage,the void fraction increases sharply,which indicates that the samples have yielded and the systems begin to enter the plastic deformation stage.The sharp increase of void fraction is caused by the dislocations nucleated from the void surface. The curves of the samples with different Mg contents show similar trends of void growth,indicating that the growth rate of voids is basically consistent in this stage.In the third stage,after the internal stress is released,the void fraction is at a stable value. In general,the void fraction of pure Al is the lowest,and the addition of Mg increases the void fraction of the system. Interestingly,the void fraction decreases with increasing Mg.

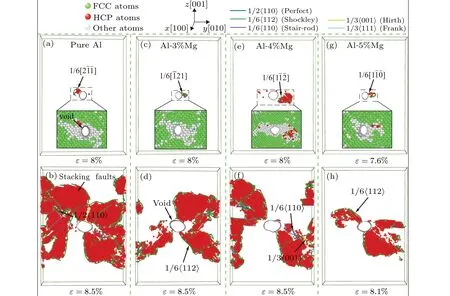
To explore more details on the deformation mechanism of Al–Mg alloys with defects, we analyze the atomic structure snapshots of samples with varied Mg at different strains(Al-2%Mg alloy is discussed in the study of void size). As shown in the insets of Fig. 6, in the initial stage of emission dislocation, the atoms along they-axis direction around void surfaces of all samples behave disordered(white atoms in the illustrations). It shows that the void has a growth trend, and the reason is that the atomic stress here is much higher than the average stress. Local stress concentration leads to higher energy of the atoms around the void,which should effectively lower the energy barrier of dislocation nucleation. Similar results have also been reported in the dislocation nucleation of polycrystal Cu by Duet al.[47]and creep in nanocrystalline metals by Wanget al.[48]When the average stress reaches the yield point, the void surface starts to emit dislocations to release the stress. According to the type of initial dislocation,Shockley dislocations 1/6〈112〉are observed in all samples,as seen in Figs. 6(a), 6(c), 6(e), and 6(g), indicating that Mg content has no effect on the type of initial dislocation. Dislocations emitted from void surface mean that the system has entered the plastic deformation stage, corresponding to the second stage in Fig. 4(a). In this stage, the dislocations emitted from the void surface propagate rapidly along the slip plane,and with the generation of new dislocations, the stress drops sharply, which leads to the rapid growth of the void. When the stress release is about to end, the disordered atomic regions undergoing plastic deformation first in the sample will rearrange into FCC structure,which will probably impede the increase of the void temporarily. Namely, the void fraction will decrease slightly.

With further loading,the dislocation density of the system enters a relatively stable value. Meanwhile, the void fraction no longer changes significantly, depicted in Fig. 4(a). Seen from Fig. 6(b), extensive stacking faults are distributed near the void of pure Al in the plastic deformation process,which is consistent with the phenomenon described by Guanet al.[21]in the deformation study of single crystal Al with a spherical void. However, with increasing Mg, the stacking faults distributed near the void decrease obviously and are primarily distributed in the diagonal direction of the simulation box,as shown in Figs. 6(d), 6(f), and 6(h). Compared with the alloy system, a more uniform distribution of stacking faults is generated around the void of pure Al, and the direction of the stacking faults is approximately perpendicular to the amorphous region of void surface in Fig.5(b). The uniform stacking faults impede the growth of void to a certain extent,which is similar to the results of the dual-phase polycrystalline Mg studied by Songet al.[49]Therefore,the void fraction in pure Al is lower than Al–Mg alloys. In Mg 2%–5% considered,the solid solution of Mg leads to the distortion of the ideal lattice, and increasing Mg makes it difficult for the dislocations to slip and propagate in the process of the tensile deformation, which impedes the growth of the void. Yet, the void fraction of Al-5%Mg alloy is still higher than that of pure Al. It is found that the Mg concentrations impede the dislocation movement,leading to a decrease of the proportion of the stacking faults around the voids,which results in a decrease of the stacking faults impeding the expansion of voids. Namely,stacking faults around the void and Mg concentrations impact the growth of the voids together. Voids are more sensitive to the stacking faults, which gives rise to the results of the third stage in Fig. 4(a). In addition, we calculate void fraction of the samples with Mg (1%, 6% and 7%). The result indicates that Mg almost has no effect on the void fraction when Mg is beyond 5%,as shown in Fig.4(b).

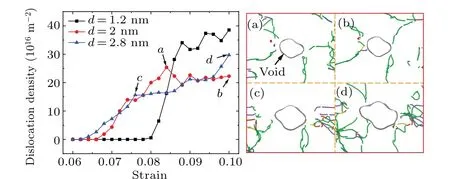
Dislocation density is another vital factor to describe the plastic deformation of the system, where the dislocation density is defined as the total length of the dislocation in a unit volume. Figure 7 shows the dislocation density of all the samples as a function of strain. The dislocation density of Al–Mg alloy is significantly lower than pure Al, and the decrease of the dislocation density is much noticeable when the Mg content is 2%. This indicates that the distortion of the ideal lattice caused by Mg effectively impedes the movement of the dislocation. Yet, the sensitivity of dislocation density to Mg concentrations decreases obviously with increasing Mg. From the insets of Figs.7(a),7(b)for pure Al and 7(c),7(d)for Al-2%Mg, the dislocation lines around the void of pure Al are long and distributed evenly, while the dislocation lines in Al-2%Mg are short and entangled.

3.2. Effect of void sizes on mechanical properties

The void size has a close relationship with the mechanical properties and plastic deformation of metals. We study the mechanical properties of the Al-2%Mg alloys with different void sizes(d=1.2 nm,2 nm,2.8 nm,3.6 nm,and 4.8 nm).

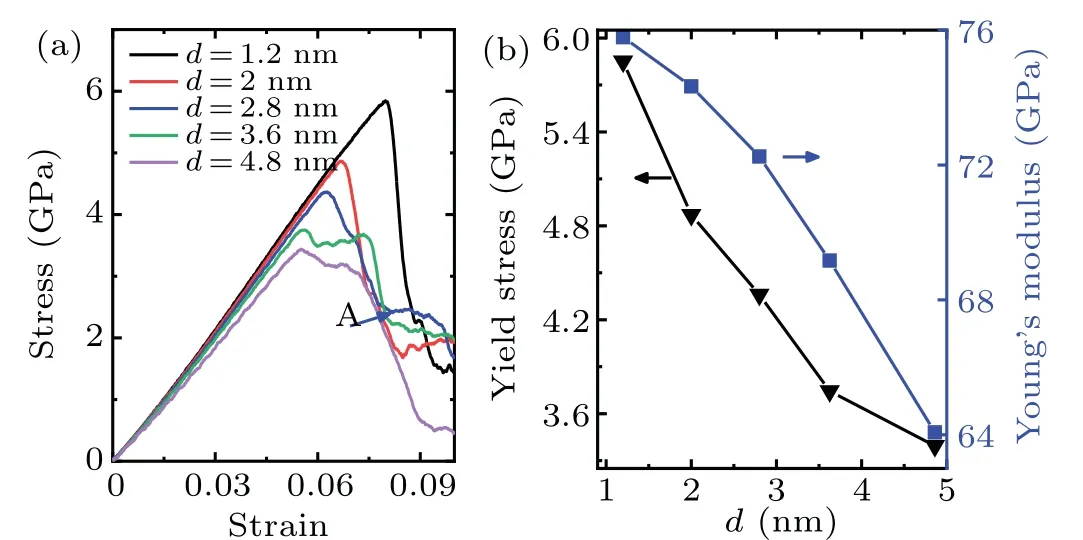
As seen in Fig. 8(a), the peak point decreases significantly with the void diameter increased. Whendis larger than 2.8 nm, the stress release process of the sample behaves gently,where a temporary‘step’phenomenon is observed,as shown in point A of the stress–strain curve. The yield stress and Young’s modulus are derived as shown in Fig. 8(b). By comparison withd=1.2 nm, the yield stress of the sample with voidd=4.8 nm decreases by 41.9%,indicating that yield stress is highly dependent on void size. In addition,void size also affects Young’s modulus,which decreases by 15.4%.

Figure 9 shows the curve of the yield stress and theR/b,

wherebis the Burgers vector. The yield stress decreases distinctly withR/bincreased,and MD results agree well with the analytical results of the Lubarda model. This model proposed by Lubardaet al.[50]is to describe the void growth caused by dislocation emission under tensile loading,where the analytical results are obtained by

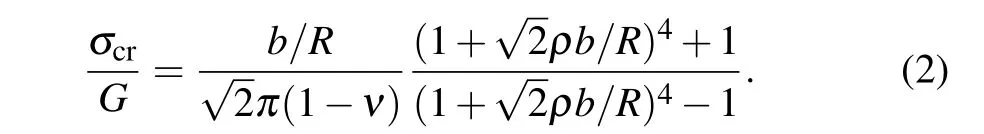
Here,we assume that the Mg atoms in the alloy are dilute sufficiently so that alloy-induced changes in elastic properties and Burgers vector magnitude are negligible. Hence,σcrrepresents the critical stress of dislocation emission, shear modulusG=26 GPa, Burgers vectorb=2.86 °A, Poisson’s ratioν=0.33,material parameterρ=1.

In order to capture the deformation mechanism depending on void size,we emphasize the plastic deformation of the Al-2%Mg alloys with different void sizes(d=1.2 nm, 2 nm and 2.8 nm). Figure 10 shows the atomic structure snapshots of the samples with varied void diameters at different strains.From the insets of Fig.10,the atoms along they-axis direction around the void surface behave disordered at the beginning of deformation. As the diameter of the void rises, the stress required to emit the dislocations from the void surface decreases,and the sample with a larger void emits the dislocations preferentially. However, it is interesting that at the same strain interval after the beginning point of deformation, the plastic deformation of the sample with a larger void is remarkably less sharp than that with a small void in Figs.10(b),10(d),and 10(f). In addition, the dislocation density also confirms what we observed. As illustrated in Fig. 11, the model with a relatively small void has a higher dislocation density, indicating that the deformation degree of the model is more severe.From the perspective of the dislocation trend,the larger the void size is, the slower the growth trend of the dislocation density is,which means that the stress release process is longer. Consequently, it shows a slow decline in the stress–strain curves.Moreover,when the dislocation density of the system remains stable,the dislocation line around the void also maintains relatively stable,as shown in Figs.11(a)and 11(b). For the transient‘step’phenomenon at point A in the stress–strain curve.The reason probably is that numerous stair-rod dislocations 1/6〈110〉are generated around the void withd=2.8 nm, as seen in Figs. 10(f) and 11(c). Because the stair-rod dislocations are relatively stable, dislocation density of the sample with voidd=2.8 nm maintains stable when the strain is 7.6%–8.6%in Fig.11,which results in the slow deformation of the system during the loading process.

3.3. Effect of temperatures on mechanical properties

It is well known that temperature holds an essential effect on the mechanical properties of nanometals. The mechanical response of Al-2%Mg alloy with voidd=2 nm is investigated at different temperatures(10 K,100 K,300 K and 500 K).As shown in Fig. 12(a), all the curves increase linearly. Beyond the peak stress in the stress–strain curves, the materials enter the plastic deformation stage. In Fig. 12(b), the effect of temperature on the yield stress and Young’s modulus is significant.At temperature of 10–500 K,the yield stress and Young’s modulus decrease sharply from 6.43 GPa and 78.98 GPa to 4.09 GPa and 66.55 GPa,respectively. As the temperature increases,the yield stress and Young’s modulus decrease due to more phonons absorbed by lattice, the increased atomic mobility and the rapid diffusion of free volume.

Hence, the atoms can be displaced more easily at higher temperature when the external loading is applied.Figure 12(c)shows the void fraction of Al-2%Mg alloy with voidd=2 nm at different temperatures.As the temperature increases,the beginning point of void growth becomes earlier. Similar results are described in the void study of single crystal zirconium.[25]After the stress release is completed,the void fraction remains relatively stable value below 300 K, while the void fraction continues to increase at 500 K.It is reasonable that when the temperature rises, the atoms in equilibrium position vibrate more violently, resulting in the instability of the lattice structure. The stress required for the atoms to leave the equilibrium position decreases,which leads to the further increase of void fraction.

4. Conclusions

In summary,the effects of Mg content,void size,and temperature on the deformation properties of cylindrical pre-void Al–Mg alloys under uniaxial tensile loading are systematically analyzed by MD simulations using stress–strain curves, void fraction, atomic configuration, and dislocation density. The results are as follows:

(1)Mg impedes the void growth effectively by deforming the lattice. The lattice distortion caused by Mg has obviously influences on the growth of the void.

(2) The void fraction of Al–Mg alloy decreases with increasing Mg content until it reaches a plateau at 5%of Mg.

(3) The critical stress required for dislocation emitted from void surface decreases with void size increased,leading to the lower yield stress of the sample with a larger void,which is in good agreement with the Lubarda model. The stress release process of the system with a larger void behaves longer,which is generated by the slow growth rate of dislocation in plastic deformation.

(4) The growth of void is sensitive to the background temperature,and the void growth occurs preferentially at high temperature. The yield stress and Young’s modulus decrease with temperature.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant No. 11502217), the Fundamental Research Funds for the Central Universities(Grant Nos. 2452015054, 2452017122, and JUSRP121042),the China Postdoctoral Science Foundation (Grant Nos. 2015M570854 and 2016T90949), the Projects of the Manned Space Engineering Technology (Grant No. 2020-ZKZX-5011), Development of Large-Scale Spacecraft Flight and Reentry Surveillance and Prediction System, the Open Fund of Key Laboratory for Intelligent Nano Materials and Devices of the Ministry of Education (NUAA) (Grant No. INMD-2019M08), and Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment and Technology(Grant Nos.FMZ202001 and FMZ202009).