A novel similarity measure for mining missing links in long-path networks

Yijun Ran(冉义军) Tianyu Liu(刘天宇) Tao Jia(贾韬) and Xiao-Ke Xu(许小可)

1College of Computer and Information Science,Southwest University,Chongqing 400715,China

2College of Information and Communication Engineering,Dalian Minzu University,Dalian 116600,China

Keywords: structural equivalence,shortest path length,long-path networks,missing links

1. Introduction

Complex networks are widely used to represent different kinds of complex systems, in which nodes are the units of a system and links are the associations between the units.[1–3]In various real systems, nodes are known but links are either missing or not present in the current frame, providing us only a partial configuration of the whole network.[4,5]For instance,genes are easy to detect in a gene regulatory network,but the interaction between genes is experimentally difficult to explore, leaving a huge gap between biological phenomena observed and mechanisms underlying.[6]Another, individuals in a social network can be easily recorded, but their relationships, such as trust or distrust, like or dislike, collaborative or betrayal, are either hidden or temporal evolving.[7]Link prediction is hence proposed to estimate the likelihood of the existence of links that are either missing links that should be connected, or nonexistent links that will exist in the future by utilizing the currently known topology.[8–11]While there are a myriad of factors that determine if two nodes are connected,network topology that represents the existing connectedness of a network is commonly used as the basis of link prediction.[12–14]Due to potential applications, link prediction has drawn a great deal of attention during the past few years, with multiple prediction methods proposed and applied to different practical networks such as co-authorship networks,[15]protein–protein interaction networks,[16]and social networks.[17]

Nowadays, the widely existing methods of link prediction can be generally fallen into two categories: similaritybased approaches in the network science domain and learningbased approaches introduced from the field of machine learning. The similarity-based approach is grounded in empirical evidence that the more similar two individuals(or equivalently two nodes of a network) are, the more likely that they know each other.[18,19]Up to now, local predictors such as common neighbor (CN), local path (LP) in similarity-based approaches are usually applied or innovated in many real networks due to their low computational complexity. For instance, L¨uet al.utilized similarity-based approaches into weighted networks (e.g.,the US air transportation network),and showed that weak ties can remarkably enhance the prediction performance.[20]Soundarajanet al.proposed a generalized common neighbor index implemented by utilizing community structure information which is added into the common neighbor, and indicated that the new index can improve the prediction accuracy in real-life networks.[21]

The learning-based approaches often consider link prediction as a binary classification problem to be solved by different machine learning algorithms.[22–24]In such approaches, features fed into classifier are used to consist of two parts: one is the similarity features from network science, another is derived from a network representation learning. The network embedding technique attempts to automate feature engineering by projecting nodes into a relatively lowdimensional latent space, which can locally preserve node’s neighborhoods.[19,25,26]After obtaining features by embedding algorithms such as DeepWalk,[27]Node2vec,[28]different kinds of machine learning algorithms can be used to build a classifier for identifying missing links.

The real networks in existing studies are almost all shortpath networks. Generally, such networks have a great number of triadic closures,hence similarity-based approaches have highly effective performance. But the performance of existing approaches is poor in long-path networks that are always very sparse. The such networks have attracted much attention in recent years. For example, Shanget al.showed that similarity-based approaches have low prediction accuracy in tree-like networks, and then proposed the heterogeneity index (HEI)which can perform better than many local similarity predictors in tree-like networks.[18]Caoet al.systematically compared similarity-based predictors with embeddingbased predictors for link prediction,and studied the shortcomings of embedding-based predictors in short-path and longpath networks.[19]

Here,we propose a new similarity-based predictor to estimate the probability that determines if two nodes are connected in long-path networks. The proposed index is associated with structural equivalence[28,29]and shortest path length[30,31]hypotheses (SESPL). The results tested on 548 real-life networks show that SESPL is highly effective in longpath networks. Our results also suggest that the failure of CN or LP is not algorithmic,but fundamental: the hypothesis that CN or LP is to only capture information within the path length 2 and path length 3,respectively. Finally,we show that a machine learning approach can exploit the discrepancy between SESPL and embedding-based methods by a random forest classifier. Taken together, our results indicate that SESPL is nearly always the best approach on 548 real networks,especially in long-path networks.

The remainder of the paper is organized as follows. We give a brief description of the link prediction task and empirical network data in Section 2. In Section 3, we introduce classical link prediction methods and propose the SESPL index.We report the main results in Section 4.Finally,Section 5 is the conclusion and discussion.

2. Problem definition and data description

2.1. Problem definition

In this paper, we focus on mining missing links. This problem is slightly different compared with analyzing the evolution of network topology in which the new nodes or links will appear and the old nodes or links may vanish.[32,33]In our study, we consider the topology of the network is static, but some links are not accurately recorded. Here, an undirected simple networkGis composed of a set of nodesVand a set of linksL, in which a node can not connect to itself(no selfloops) nor share more than one link with another node (no repeated links). In the problem of link prediction,a predictor takes some features of the network and assigns a scoreSabto each pair of nodesaandb,which is proportional to the chance that nodesaandbshould be connected. BecauseGis undirected, the score is symmetric,i.e., Sab=Sba. The scores for node pairs that are not currently connected are sorted in descending order and the top candidates are likely missing links.

TheLlinks of a real-life network are randomly divided into two exclusive sets: the training setLTand the probe setLP. The links inLPare considered as currently missing and need to be inferred from network topology given by the links inLT. In this work, we apply the typical division[8]that assigns 90%of theLlinks toLTand the remaining 10%toLP.In order to test the performance of link prediction,another probe setLNis used as the control group ofLP, which is composed of randomly chosen nonexistent links usually with the same size ofLP. The prediction quality is measured by comparing the score of predicted links inLPandLN. If out ofntimes of independent comparisons, there aren′times that the missing link inLPhas a higher score than the nonexistent link inLN,andn′′times that the missing link and the nonexistent link have the same score,[8]the result of AUC can be calculated as

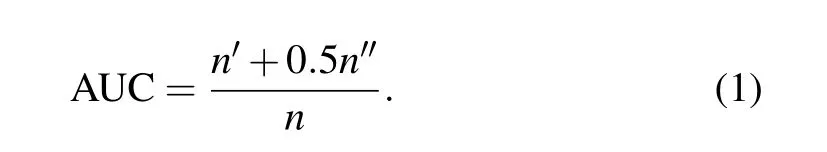
2.2. Data description

In this study, we compare the performance of link prediction on a large corpus of 548 real networks from the CommunityFitNet corpus,[24]where there is a comprehensive description of these real networks. This structurally diverse corpus includes biological (179, 32.66%), social (124, 22.63%),economic (122, 22.26%), technological (70, 12.77%), transportation(35,6.39%),and information(18,3.28%)networks.Overall, the average number of nodes in all 548 networks is 563.56 where the max number of nodes is 3353. And the average number of links in all networks is 1215.84 where the max number of links is 7562. In addition, the average clustering coefficient of all networks is 0.271 in which the max one is 0.936. Here,we define〈d〉as the average shortest path length and count the distribution of〈d〉on 548 real-world networks in Fig.1.

Fig. 1. The distribution of average shortest path length (〈d〉) on 548 real networks. The red dash line is a turning point in which 〈d〉 is about 9.Short-path networks are located at the left of the red dash line,meanwhile,long-path networks are located at the right.

Nowadays, the definition of short-path or long-path networks is not absolutely clear. In Ref.[19],the authors defined that the networks with〈d〉＞15 are the long-path networks. In this study,according to the distribution of〈d〉in which〈d〉=9 is a turning point (Fig. 1), we define that the networks with〈d〉＜9 are short-path networks,otherwise the networks with〈d〉≥9 are called long-path networks. In 548 real networks,there are 164 long-path networks that primarily contain biological,technological,transportation,and economic networks.Here,we visualize one of long-path networks and one of shortpath networks in Fig.2.The long-path network almost forms a chain-like or tree-like network which has many open triangular structures in Fig.2(a). In contrast, the short-path network has a myriad of close triangular structures(high clustering coefficient)in Fig.2(b).

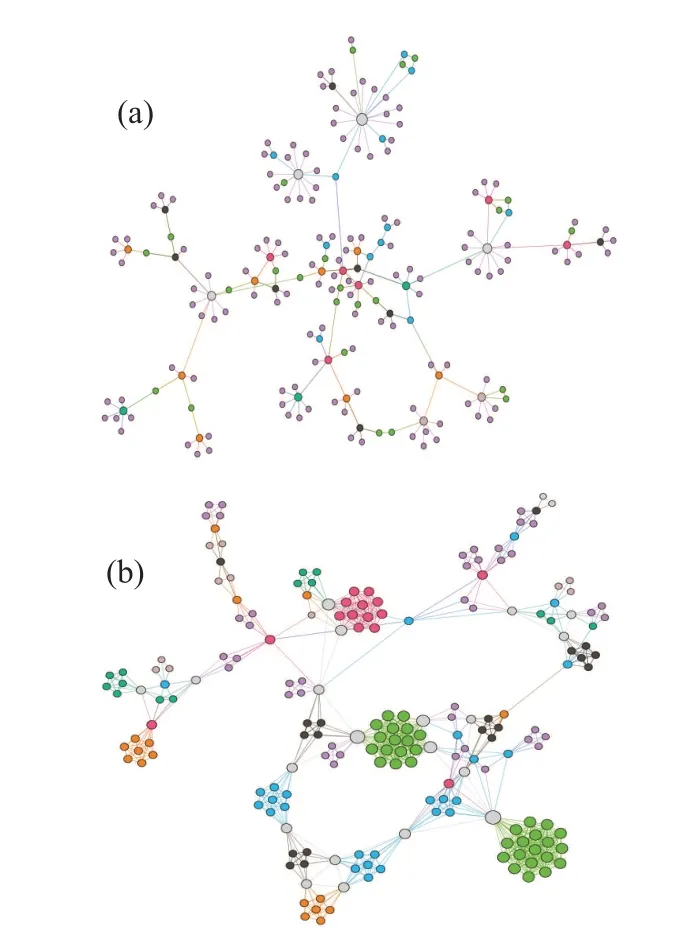
Fig. 2. Examples of long-path networks and short-path networks. (a) The long-path economic network has 200 nodes and 207 links, and its 〈d〉 is 7.52. It sampled from the original economic network with〈d〉=10.87 using breadth-first search(BFS)algorithm. (b)The short-path social network has 200 nodes and 910 links,and its〈d〉is 4.73.It sampled from the original social network with 〈d〉=6.31 utilizing the BFS algorithm. The size and color of nodes are determined according to the degree of each node.

3. Methods of link prediction

Here,we describe in detail two categories of link predictors:similarity-based predictors and embedding-based predictors. In addition, we elaborate in more detail the method of SESPL.

3.1. Similarity-based predictors

In the predictors based on structural similarity, the simplest predictor is the method of common neighbor(CN).The CN predictor is first proposed by Lorrainet al.,[29]then Newman used this index to study collaboration networks.[34]The basic idea is that two nodes that share the same neighborhood are likely to share other common features hence are likely to have a link.In the problem of link prediction,the pair of nodesaandbis assigned a scoreSabthat depends on the set of neighborhoods the two nodes share. The method of CN directly counts the number of common neighbors as

wheren(a)denotes the set of neighborhood nodes that nodeahas.Some predictors based on CN have been proposed one after another,such as Salton index(Salton),Adamic-Adar index(AA), resource allocation index (RA). Our work has shown that these indices can be categorized into CN-based predictors. Therefore,we here select CN as the representative of all CN-based predictors.

The predictors based on CN have been widely used in different fields because of the simplicity and interpretability.[35–37]However, it is difficult for CN-based predictors to predict missing links when the network does not have rich close triangle structures. One more accurate method is the local path (LP) index that catches up with more path information.[38,39]The LP index not only considers the paths between nodeaandbwith length 2 but also further considers that with length 3. Yielding whereA2abis the number of the paths with length 2 between nodesaandb, andβis a free parameter controlling the path weights. Many path-based predictors have been proposed and applied to real networks. Here,we employ LP and Katz as the representative path-based predictors for comparison.

Another well-known method is preferential attachment index(PA)which is based on the observation that the probability of a new link between nodes increases as their degrees.[41]This theoretical model leads to the concept of “the rich get richer”,which generates the power-law degree distribution observed in many real networks. Hence, the probability that a new link will connectaandbis proportional to

3.2. Embedding-based predictors

Recently, network embedding techniques that are instances of representation learning on networks have been widely applied in link prediction.[42–45]Embedding-based predictors are derived from network embedding techniques,which attempt to automate feature engineering by projecting nodes in a network into a relatively low-dimensional latent space, to locally preserve node’s neighborhoods. In this study, after representing nodes in a network as vectors, we apply t-distributed stochastic neighbor embedding (t-SNE)algorithm[46]to reduce the vector dimensions. The methods of dimension reduction are commonly divided into linear and nonlinear approaches. For instance, both principal component analysis (PCA) and linear discriminant analysis(LDA)can perform a linear mapping of high-dimensional data to a lower-dimensional space. While the t-SNE algorithm is a nonlinear dimensionality reduction technique for complex high-dimensional datasets. Here, we use t-SNE to reduce the embedding vector of each node into ten dimensions space.And then we apply a Hadamard product function[47]to obtain the vectors of corresponding links, which will be used as features to input into a random forest classifier. In this study, we consider three popular network embedding algorithms, DeepWalk,[27]Node2vec,[28]and GraphWave[48]for comparison.

DeepWalk is the pioneered work about learning latent representation of nodes in a network.[27]The authors applied natural language processing technology into network science.The DeepWalk uses local information obtained from truncated random walks to learn latent representations by treating walks as the equivalent of sentences. The representation vector learned by the DeepWalk reflects the local structure of a node. The more common neighbors(and higher-order neighbors) between two nodes share, the shorter distance between the corresponding two vectors of nodes.

Node2vec mainly adopts homogeneity and structural equivalence to explore diverse network structural information.[28]For homogeneity, the Node2vec can learn a latent representation of nodes by embedding nodes from the same network community closer together. For structural equivalence,the Node2vec can learn latent representations via nodes that share similar roles should have similar embedding vectors. The embedding vectors by Node2vec can preserve diverse types of network information and be constructed for link prediction, which makes prediction performance more accurate.

GraphWave is a scalable unsupervised method for learning node embeddings based on structural similarity in networks.[48]The GraphWave uses a novel way that treats the wavelets as probability distributions on the network. Intuitively, a node propagates an energy unit on the network and characterizes its neighbor topology based on network response to this probe. The GraphWave shows that the nodes with similar structures can be closely embedded together in vector spaces. The GraphWave is the same as the Node2vec,it takes advantage of similar structure information to embed nodes into a low dimension space.

3.3. The SESPL predictor

In this section, we will present in more detail the proposed SESPL predictor. Obviously, the higher score computed by a similarity-based predictor means that this index is a better predictor. In CN-based predictors, the idea behind is that the more common friends two individuals have,the more likely that they know each other. The CN-based predictors and path-based predictors show high performance in real social networks which are usually high clustering coefficients,but fail to predict the existence of a link between two nodes in long-path networks. The main reason is that these predictors are not designed to capture long-path information existing in many real-life networks. While the Katz predictor is based on global structure information, it is extremely computationally expensive.Meanwhile,long-path networks such as technological,transportation,and economic networks are ubiquitous in real-world systems. Therefore,it is necessary to design an efficient and semi-local algorithm for link prediction,especially for big-size and long-path networks.

Here we make two hypotheses that are in line with our intuition. The first hypothesis is that the more similar role of two nodes, the more likely it is for them to communicate or promote cooperation. The role may be defined as a term conceptualized by certain nodal attributes, meaning that the role is a function or identity of a node that explains the status of the node in society.[40]For example, it is easier for presidents of two countries to meet, compared to other ordinary people. Another, companies with similar properties are more likely to reach agreements and cooperate together. However,individuals in real life usually suffer from unavailable and unreliable attribute information. Hence, it is difficult for us to quantify the similar role between nodes from attribute information. Fortunately,recent studies indicated that the structure building by the nodes with the same identity or properties can be mapped into a similar structure role,in which this process is used to express as structural equivalence.[28,48]This further shows that our first hypothesis can imply that the nodes having similar structural roles should link closely together.Therefore,we can take advantage of structural equivalence to quantify the similarity between nodes.

The second hypothesis is that the shorter physical distance between two nodes, the easier they are to form a link.This may indicate the deep significance of the Chinese proverb— “better is a neighbor that is near than a brother far off”.For instance,in a realistic transportation system,architects often consider a variety of factors to make the highway as close as possible between the existing two transportation junctions when the government is planning to build a new highway.Similarly, technicians can add a cable between the two nearest switches so that it can reach the asynchronous and efficient transmission of information.

Overall, we mainly consider both structural equivalence and shortest path length to quantify the similarity between two nodes, namely, the SESPL index. Intuitively, we note that structural equivalence is often sufficient to characterize local neighborhoods accurately. Here we quantify the structural equivalence of two nodes by only taking into account the first-order and second-order neighbors. Quantifying similarities and determining isomorphisms among graphs is the fundamental problem in graph theory,with a very long history.[50,51]Recently,Schieberet al.proposed an efficient and precise algorithm for quantifying dissimilarities among graphs, which is based on quantifying differences among distance probability distributions extracted from networks.[52]However, this method has a high time complexity for big-size networks.Therefore, our idea to measure the structural equivalence,SE(a,b), of two local structures is to associate to the degree centrality of each node which can represent nodes’connectivity. The degree centrality shows that a node is central if it has many links with other nodes in a network.[53]Degree centrality of a nodeican be defined as

whereJ(Pa,Pb) is the Jensen–Shannon divergence between the local structure centered on nodeaandb,respectively.

The shortest path length hypothesis mentioned above implies that the shorter distance between two nodes is,the higher probability they have to form a link.Here,we definedabas the shortest path length of a node pair(a,b)in a real-life network.The important feature ofdabis that it has a promoting effect on node pairs with short distances and an inhibitory effect on node pairs with long distances. The link prediction task is that mining the chance that determines if the disconnected node pair is connected,hencedabshould be longer than or equal to 2. Hence,given a disconnected node pair(a,b),the likelihood score of link(a,b)is defined as

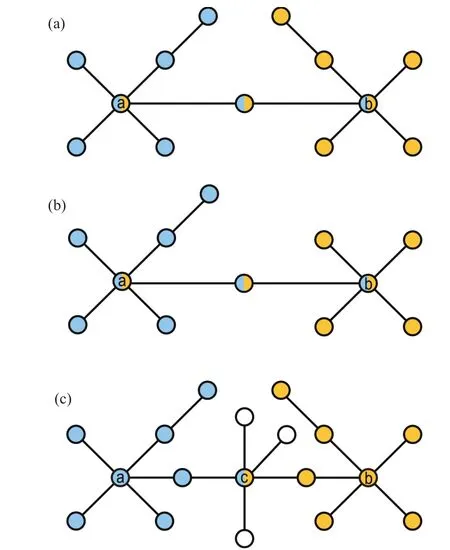
Fig. 3. The local structure of node a or b in each toy network. Different colors indicate the ownership of a node. The blue nodes constitute the local structure of node a in each toy network,the yellow nodes constitute the local structure of node b in each toy network.

When we compute SESPL, there are two parts. Firstly,the time complexity isO(Nk)for calculating structural equivalence if the time complexity to traverse the neighborhood of a node is simplyk. Then,we use the Dijkstra algorithm[55]to search the path,its time complexity isO(N2). Taken together,the complexity of SESPL index is roughlyO(N2).

4. Experimental results

4.1. Performance evaluation of SESPL

To perform overall the predictive ability of SESPL, we quantify its performance on 548 real-world networks. Here,all results are based on the average over 1000 independent runs of simulation.Considering different properties of real-life networks,we divide them into short-path and long-path networks according to Fig.1. As shown in Fig.4,we first compare the performance of each predictor across 384 short-path networks.Although the predictive performance of SESPL is higher than that of CN,PA,and HEI,it is lower than that of LP or Katz on 384 short-path networks. This exhibits that SESPL has no advantage on short-path networks. It also verifies that LP is the best algorithm in short-path networks when utilizing limited resources.[9,38]

In contrast,the performance of SESPL on 164 long-path networks is shown in Fig.4,which is higher than all the other predictors, including LP or Katz algorithms. The LP predictor has relatively poor performance in long-path networks,because LP only takes the advantage of 3-order path information.Although Katz can also achieve high performance in long-path networks,it has high computational complexity and lower performance than SESPL.To show the effect of local structure in SESPL predictor, here we extend the definition of node’s local structure. As shown in Fig. 4, the most obvious finding to emerge from this further experiment is that SESPL with a high-order structure(SESPL1 or SESPL2)has little contribution on short-path networks,but has a gain on prediction performance in long-path networks. Taken together, the original version of SESPL may be suitable for all networks.

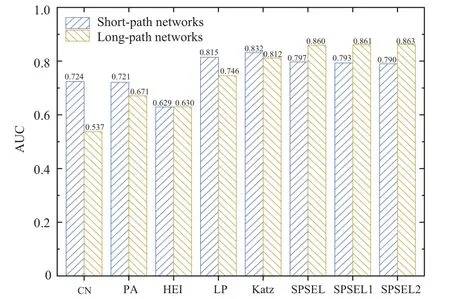
Fig. 4. The AUC results of 6 similarity-based predictors in short-path and long-path networks. Here, we expand two versions of SESPL, namely,SESPL1 and SESPL2. In SESPL1 version, the local structure in Eq. (9)consists of the first-order to the third-order neighbors of a node. In the same way,the local structure in SESPL2 version consists of the first-order to the fourth-order neighbors of a node.

In general, it is more difficult to predict missing links in long-path networks than short-path networks, because the long-path networks are more sparse. The performance of CN,PA,LP,and Katz algorithms support this conclusion in Fig.4.In contrast,SESPL and HEI have a gain on prediction performance from short-path to long-path networks,which indicates that they are suitable algorithms for long-path networks. One of the more significant findings to emerge from this study is that SESPL not only has a 7.90% performance improvement in long-path networks compared with short-path networks,but also is higher than all the other algorithms in long-path networks.And we also find that the predictive performance of the SESPL predictor is more advantageous compared with other similarity algorithms when the average shortest path length of the network is longer.

Finally, to compare the difference between SESPL and each embedding-based predictor,we characterize their predictive performance by training a random forest classifier. Here,we randomly divide 80%of theLlinks toLTand the remaining 20%toLP,and another probe setLNis composed of randomly chosen nonexistent links with the same size ofLP. Hence,we compute each feature such as SESPL, CN, PAet al.by using theLT. We then take 10% ofLPand 10% ofLNto train the random forest classifier and the remaining 10%of those to predict.After obtaining the predictive probability of each link,we quantify the performance of each feature using the Eq.(1).

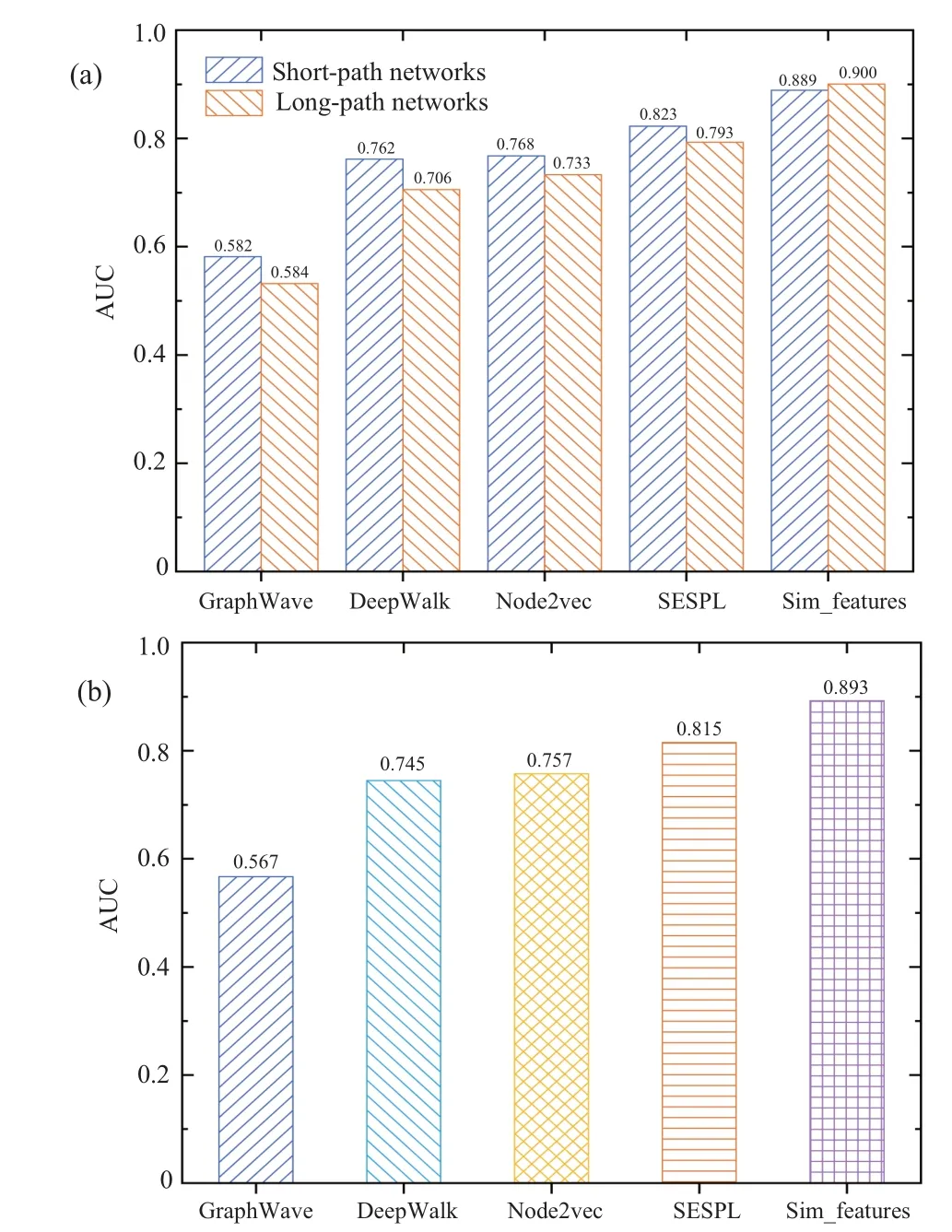
Fig. 5. The results of machine learning on 548 real networks. Here, the parameter of each embedding algorithm is default sets. Each embedding vector is reduced into 10-dimensions space as 10-dimensions feature. The score of SESPL as a feature is inputted into a random forest classifier. (a)The results of machine learning on short-path or long-path networks. (b)The results of machine learning on 548 real networks.

As depicted in Fig. 5(a), the single most striking observation to emerge from the experimental comparison is that the predictive performance of SESPL is higher than that of each embedding algorithm regardless of whether short-path networks or long-path networks. The further analysis shows that SESPL predictor significantly outperforms each embeddingbased predictor on 548 real-world networks as shown in Fig.5(b). This may be because SESPL can capture two kinds of network properties, that are, structural equivalence and physical distance. By contrast,GraphWave has the worst predictive performance (Fig. 5), which might be due to the fact that GraphWave only keeps structural equivalence when embedding nodes in a network into a relatively low-dimensional latent space.[48]In addition, Node2vec has relatively higher performance than DeepWalk (Fig. 5), this is mainly because Node2vec has a flexible neighborhood sampling strategy that can balance structural equivalence and homogeneity.[28]Taken together, our results also show that embedding-based predictors perform poorly on these networks.[24]More importantly,in spite of short-path networks or long-path networks,combining 6 similarity-based predictors can achieve the best predictions as shown in Fig.5.Here the Sim features is that combining the 6 similarity-based predictors(CN,PA,HEI,LP,Katz,and SESPL). We take the score of 6 predictors to combine them into 6-dimensional features, and then input them into a random forest classifier. The result in Fig. 5 supports the recent work that combining similarity-based methods can produce higher accurate predictions than that of each embedding algorithm.[24]

In addition,we also evaluate the effect of embedding dimensionality on method performance. What is striking about the figures as depicted in Fig.6 is that while each embedding algorithm has a little gain on prediction performance, it can be ignored. This indicates that the dimensionality reduction technique can cut down the computational complexity when keeping the loss of prediction accuracy small. As a whole,SESPL we proposed is a state-of-the-art predictor, especially in long-path networks.

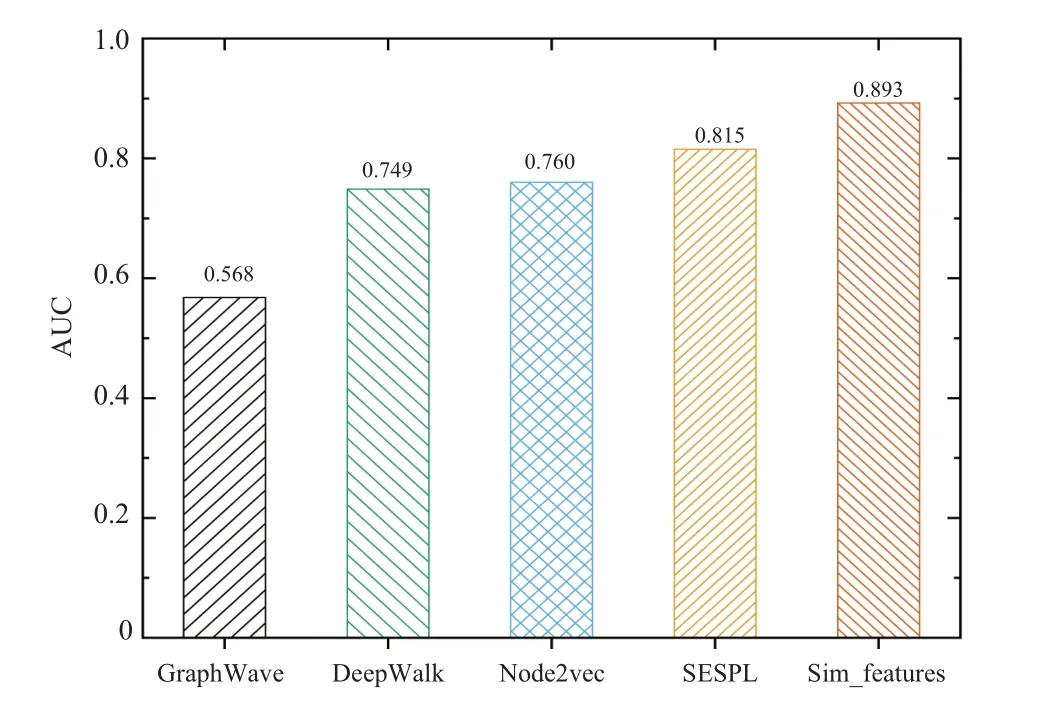
Fig. 6. The results of machine learning applied to 548 real networks.Each embedding vector keeps the original 128-dimensions space as a 128-dimensions feature. The other parameters keep in the same way as given in Fig.5.

4.2. Similarity-based predictors correlation detection

To deeply explain that SESPL is the useful feature for link prediction, we utilize maximal information coefficient(MIC)[56]to quantify the correlation among six similaritybased features. The correlation between two predictorsSiandSjis defined as MIC(Si,Sj). The larger the MIC(Si,Sj)is,the stronger the substitutability between two featuresSiandSj.MIC(Si,Sj)=0 shows thatSiandSjare independent of each other.

As depicted in Fig.7,there is a strong correlation between predictors in each red dot-line box, while the correlation between predictors in different red dot-line boxes is weak. Overall,the correlation among SESPL,CN,LP,and Katz is different in short-path and long-path networks,while the correlation between PA and HEI is the same. As shown in Fig. 7(a), the six predictors can classify as two kinds of features. One is that SESPL, CN, LP, and Katz can all capture common neighbor information, so the correlations among them are strong. The other is that the correlation between PA and HEI is strong because of utilizing degree information.

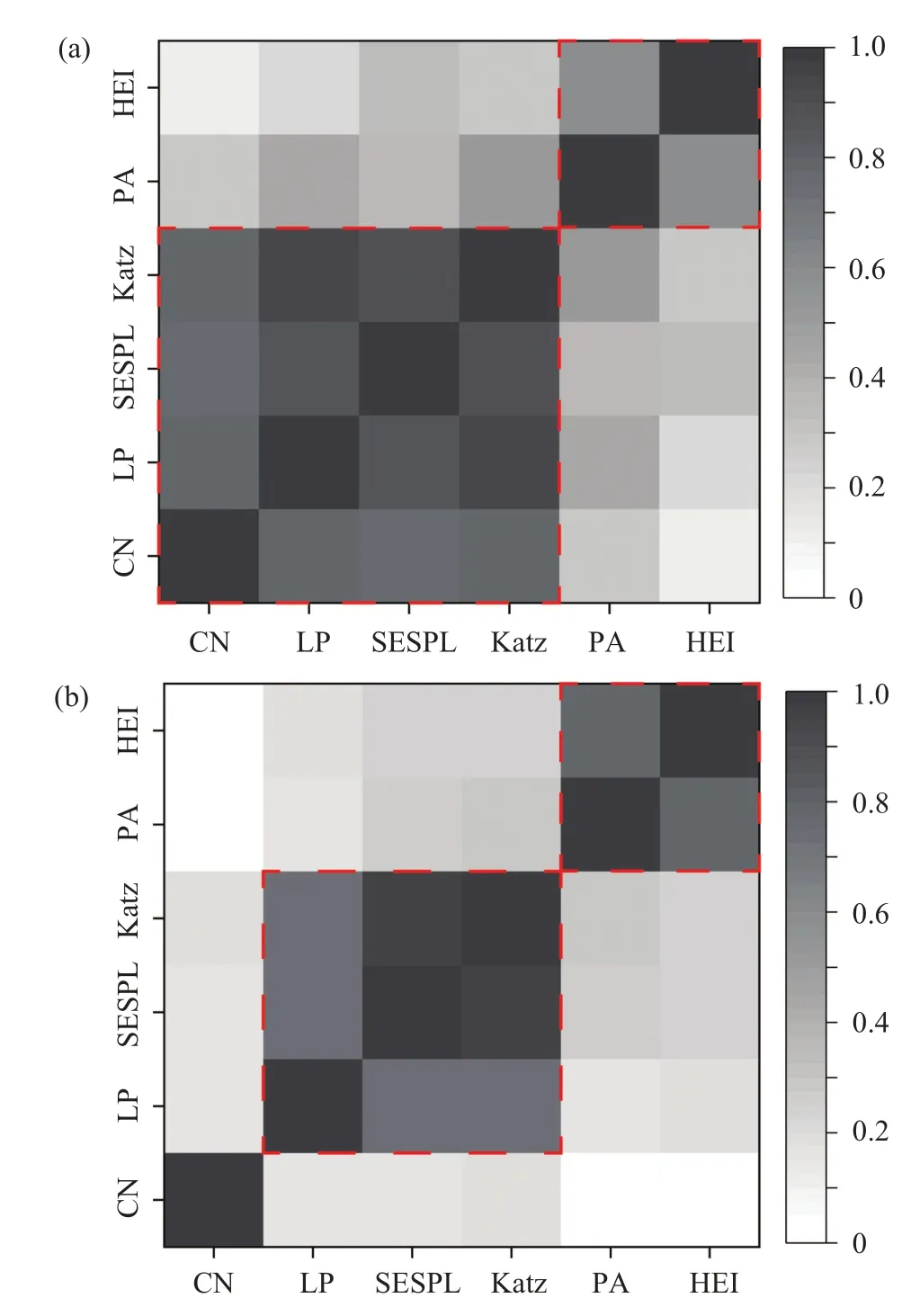
Fig.7. The heat map of MIC correlation matrix by the scores of links(i.e.,LP and LN)among six topology similarity-based features. The color intensity indicates the strength of the correlation. (a) The heat map of average MIC on 384 short-path networks. (b)The heat map of average MIC on 164 long-path networks.

For long-path networks,however,CN is almost independent of other predictors because it can not capture the highorder path information in Fig.7(b). Therefore,roughly speaking, there are three kinds of features in long-path networks.The LP, SESPL, and Katz predictor can be classified as the same feature. But strictly speaking, the correlation between SESPL and Katz is the strongest because of capturing highorder path information. This means that SESPL and Katz are the most similar feature. Hence the SESPL can totally replace the Katz when caring about limited resources. Taken together,SESPL can be regarded as a supplement to structure similarity features of long-path networks.

5. Discussion and conclusion

To summarize, we proposed a new predictor to estimate the probability of a link between two nodes that determines if the two nodes are connected in long-path networks,called the SESPL,which can capture the principles of structural equivalence and the shortest path length. The SESPL is highly effective and efficient compared with other similarity-based predictors in long-path networks. We also exploit the performance of the SESPL predictor and embedding-based approaches via machine learning techniques,and the experimental results indicate that the best prediction performance comes from the SESPL feature. Finally, according to the matrix of maximal information coefficient among all the predictors, the index of SESPL can be regarded as a supplement to structure similarity features of long-path networks.

In this work, the principles of the structural equivalence and the shortest path length are integrated into similarity-based predictors, which can provide new insights into link prediction. The structural equivalence is efficiently quantified by the Jensen–Shannon divergence. In the future,on the basis of the current work, the promising research extensions about what kind of network should utilize high-order structural information can be performed. In addition,for simplicity reasons,our index does not take link weights into consideration. The link weights,measuring how frequently two nodes are associated,is an important variable. We will also try to apply SESPL predictor into the link prediction of weighted networks.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant Nos. 61773091 and 62173065), the Industry-University-Research Innovation Fund for Chinese Universities (Grant No. 2021ALA03016), the Fund for University Innovation Research Group of Chongqing (Grant No.CXQT21005),the National Social Science Foundation of China(Grant No.20CTQ029),and the Fundamental Research Funds for the Central Universities(Grant No.SWU119062).