Role of the zonal flow in multi-scale multi-mode turbulence with small-scale shear flow in tokamak plasmas
2022-06-29HuiLi李慧JiquanLi李继全ZhengxiongWang王正汹LaiWei魏来andZhaoqingHu胡朝清
Hui Li(李慧) Jiquan Li(李继全) Zhengxiong Wang(王正汹) Lai Wei(魏来) and Zhaoqing Hu(胡朝清)
1Key Laboratory of Materials Modification by Beams of the Ministry of Education,School of Physics,Dalian University of Technology,Dalian 116024,China
2Southwestern Institute of Physics,Chengdu 610041,China
Keywords: drift waves,turbulence,nonlinear phenomena,plasma simulation
1. Introduction
Nonlinear interaction of multi-scale multi-mode instability plays significant roles in critical issues of magnetic fusion plasma. Simulations with both gyro-kinetic[1]and fluid model,[2,3]were utilized to illustrate the nonlinear interaction between islands and turbulence. Experimentally, several works reported the interaction mechanisms between large-scale magnetohydrodynamic instabilities and microturbulence.[4–10]Furthermore, it was displayed the poloidal shear flow generated by islands played the essential role in the interaction between the islands and transport process.[11–13]It is well known that the shear flows have great effects on stabilizing various fluctuations in wide scale in tokamak plasmas. The effect of theE×Bshear flow on the ion-scale turbulence and associated transport has been extensively studied theoretically and numerically as well as experimentally.[14]TheE×Bflows play a central role in regulating the saturation level of the turbulence and turbulent transport.[15]TheE×Bvelocity shear caused the reduction in turbulence and transport.[16]On the other hand, the flow shear may also make a destabilizing contribution as well.[17]One typical example is the radial gradient of velocity for Kelvin–Helmholtz (KH) instability driven by the flow shear.As is well known,when the strength of the shear flow exceeds the critical value, the KH instability becomes unstable.[18]Resent study illustrated that the shear flow may cause the KH mode exhibiting either regular or irregular oscillations.[19]Relatively,dual roles of the shear flow in impacting with both macro-and micro-scale fluctuations have been unveiled in an electromagnetic(EM)turbulence. It has been shown that besides stabilizing the micro-scale instability as expected, the shear flow dramatically enhances the macroscale, long wavelength fluctuations.[20]
It is well recognized that zonal flows self-generated by turbulence play an important role in regulating turbulence,reducing transport level, and thus improve plasma confinement in fusion plasmas.[21,22]Moreover, zonal flows can not only stabilize the fluctuations through flow shear but also play a major role in turbulence saturation. Such dynamics usually occur in the turbulence with single drive force in a limited spectral range. However,for cross-scale turbulence,e.g.,mixed ion temperature gradient (ITG) and electron temperature gradient (ETG) driven turbulent fluctuation, small-scale zonal flow generated by the ETG turbulence may impact on the ITG turbulence through some peculiar mechanisms rather than only the flow shear. It has been clarified that the small-scale zonal flows result in a radially nonlocal mode coupling of ITG fluctuations, leading to the transport intermittency. In tokamak plasmas, another important short wave-length instability,the so-called collisionless trapped-electron mode(CTEM)commonly exists, which is driven by both electron temperature and/or density gradients.[23,24]The radial short wavelength spectrum of the zonal flow is mainly distributed in a wide range ofqrρi~[0.4,1.5].[25]It was analyzed theoretically which also exhibit a relatively short radial scale of the zonal flows withqrρθi~1(ρθiis the ion poloidal gyroradius)in CTEM turbulence.[26]Furthermore,as the zonal flow is generated and enhanced,it may drive the KH instability when the flow shear is beyond a threshold. Such secondary KH mode can not only interact with the ambient turbulence, but also generate zonal flows,[27,28]which leads to a complex nonlinear multi-scale multi-mode interaction system. These dynamics have been demonstrated in the Rogers’s work,[29]that the strong KH-like modes were excited which acted to break up the primary mode accompanied with the production of zonal flows. Furthermore,the effect of a narrow sub-Alfv´enic shear flow layer near the minimumqminof the tokamak safety factor profile in a configuration with reversed central shear was analyzed.[30,31]
Motivated by the issues above, consistent simulations of the time evolution of an EM ITG turbulence are carried out accompanied with an externally imposed radial small-scale shear flow. In the simulation, the shear flow is fixed and presumed to be robust CTEM-generated zonal flow with radial wave numberqrρi≤1.0.[32–34]Particularly,strong shear flow is considered so that the long wavelength KH instability is excited. Therefore, the physical model here is set as a highly complicated multi-scale multi-mode EM turbulence system involving the ITG and KH modes with wide radial spectrum of zonal flows as well as a constant small-scale shear flow externally imposed. Results obviously reveal the key role of the zonal flows which cause the periodic intermittency of the multi-mode fluctuation in cross-scale turbulence. This behavior is different compared with our previous work imposed with moderate small-scale shear flow. In preceding paper,complex linear and nonlinear interaction before the regular intermittency occurs has been focused. Therefore, in this work, we mainly analyze the underlying mechanisms in the oscillation phase.[35]Simulations show that the odd symmetric components of zonal flow(same symmetry as the external flow)make the radial parity of the KH mode alteration through adjusting the drift velocities at two sides of the resonant surface so that the KH mode becomes bursty firstly. Afterwards,the ITG intermittency follows due to nonlinear mode coupling among the KH, EM ITG modes and the shear flows including the zonal flows and the external small-scale shear flow.
The remainder of this paper is organized as follows. The physical model and simulation setting are detailed in Section 2. Section 3 is devoted to nonlinear simulations and modeling analyses. The zonal flow dynamics in multi-scale multimode turbulence are elaborated. In Section 4,turbulent transport is discussed. Finally,a summary of key results is given in Section 5.
2. Physical model and simulation setting
To simulate the time evolution of multi-scale multi-mode turbulence with small-scale shear flows and understand the underlying mechanism of the nonlinear interaction of crossscale EM turbulence including the zonal flow dynamics, a 5-field Landau-fluid model is employed in slab geometry.[36,37]This can also consistently capture the excitation of secondary KH mode when the flow shear is larger than the stability threshold.[35]The highly complex nonlinear interaction dynamics of cross-scale turbulence with ITG as well as KH modes are governed by normalized evolution equations of perturbed densityn, the vorticity ∇2⊥φ, parallel ion velocityυ‖,magnetic fluxψ(corresponding to the parallel vector potential throughA‖=-ψ),as well as ion temperatureTias follows:

with the operatorsdt=∂t+υ0∂y+ ˆez×∇⊥φ ·∇⊥, ∇2⊥=∂2x+∂2y,ηi=Ln/LTi,β= (8πn0Ti0)/B2,j‖= ∇2⊥ψ, and∇‖=∂z+ˆsλarcsinh(x/λ)∂y-βˆez×∇⊥Ψ·∇⊥with magnetic shear ˆs=Ln/Lsandλrepresenting the gradient length of axial equilibrium current. Here,x,y,andzcorrespond to the radial,poloidal, and toroidal directions in a toroidal plasma, respectively. And a finite difference method is applied inxdirection with a fixed boundary condition atx=±Lx/2 and Fourier decomposition is used in theydirection. The normalizations are expressed as usual.[35]The code has been well checked for the convergency with enough high resolutions in radial real space and mode number spectral space. Other main parameters used in simulations areλ=1.5, ˆs=0.1 and the classical cross-field dissipations are set asDU=Dn=η⊥=χ⊥=0.01 which are included to damp smaller-scale fluctuations. It has obvious influence on the evolution of potential energy, as shown in Appendix A. In addition, the resistivityη=0 is taken here to make consistency with the CTEM in collisionless plasma.This implies that the resistive tearing mode should be stable in cross-scale EM turbulence involving MHD and ITG modes.
Nonlinear evolution equations(1)–(5)can be numerically solved by an initial value code with the same numerical setting as in Ref.[35]. The small-scale shear flow externally embedded in cross-scale EM system as a coherent structure is set as
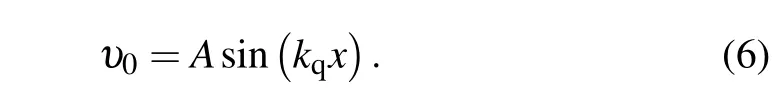
As illustrated in the introduction,the wave numberkqis set in the range ofkq=[0.5,1.2]which considers the typical characteristic wave number of the CTEM-generated zonal flows.
3. Numerical simulation and modeling analysis
Simulations are performed to investigate the evolution dynamics of multi-scale multi-mode turbulence with strong small-scale shear flow(present from onset time). In this work,two dominant modes driven by independent drive force are involved with distinctly separated scales. One is the long wavelength KH mode destabilized by small-scale flow shear with the threshold shear velocityA=0.64 presented in our previous work.[35]Meanwhile, the other one is the ion-scale ITG mode at relatively shorter wavelengths. Both are electromagnetic type fluctuations here although the resistive MHD modes are stable due to the zero resistivity for simplicity.
For strong shear flow withA=0.9, a periodic intermittency (or oscillation-like for shorter periods) of the fluctuating energy emerges remarkably for all modes except for the dominant ITG component(ky=0.8)in the quasi-steady state,as shown in Fig.1. Complex linear and nonlinear interaction among the KH,EM ITG modes and the shear flows including the zonal flows and the external small-scale shear flow before the regular intermittency occurs has been discussed in preceding paper.[35]We focus on the understanding of the underlying mechanisms behind the intermittency phenomenon (in the oscillation phase)in this work. Generally,it is recognized that the zonal flow is created nonlinearly through the Reynolds stress in the micro-turbulence,and characterized by a low frequency, symmetric and large radial scale structure. Specifically, the zonal flow is also identified as a beat wave of two pump components accompanied with opposed frequency and poloidal wavenumber through three-mode coupling.[38]The detailed analysis of the mode–mode coupling was discussed in the Refs.[35,39].
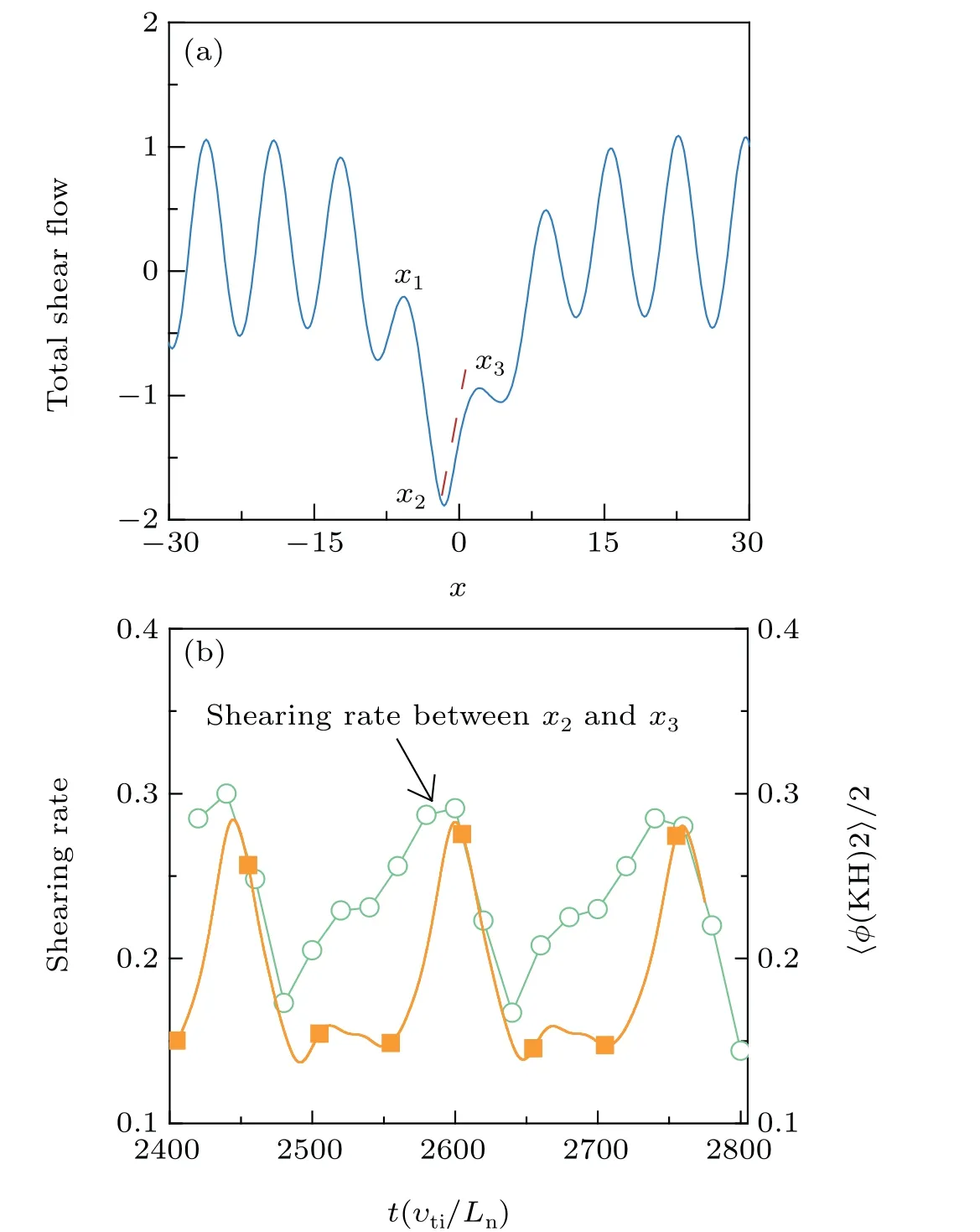
However, as the presence of the sinusoidal-type smallscale shear flow, the newly generated zonal flow may be influenced depending on the symmetry and amplitude of the external shear flow. In the linear stage,no matter how large the flow shear velocity given externally,the eigen structure of the KH mode potential is symmetric with the even parity around the rational surface. When going into the nonlinear phase,the symmetry of the large-scale structure is changed slightly because the newly generated zonal flow may modify the symmetry of the equilibrium shear flow slightly. As stronger KH mode is generated with strong external shear velocity imposed,the equilibrium shear flow, either the symmetry or the amplitude, is changed greatly in the nonlinear stage. The mechanism of this process can be elucidated clearly through the evolution of shearing rate around the rational surface as shown in Fig. 2. The total flow shear (including the givenυ0and selfgenerated zonal flow)is obviously changed at three positions marked asx1,x2,x3.To visualize such a process,about two periods,e.g.,t=2420–2800 in the oscillation phase,are chosen to examine the modification of shearing rate around the rational surfacex=0. Remarkably, as shown in Fig.2(b), the localized shearing rate(slope of the red dashed line in Fig.2(a))also exhibits a periodic oscillation,which is in the approximative phase with the evolution of KH mode. In the sense, it is believable that the oscillation of the energy evolution is associated with the modified shear flow dynamics (including the givenυ0and self-generated zonal flow).
As the energy evolution of the KH mode is characterized by periodic oscillation, its structure is analyzed. Firstly, the profile of the KH structure has a shift away from the rational surface, which may correspond to correction of theυzfodd part to the imposed flowυ0. Secondly, the symmetry breaking of the KH mode is observed. As shown in Figs.3(b)and 3(d),two kinds of typical eigen states of the KH mode appear alternately, which are characterized by the potential fluctuation with even or odd parity in the oscillation phase. Interestingly, as the zonal flow increasing, the modification of the equilibrium shear flows profile varies sensitively, leading to obvious distortion of the mode structure until coming to the state with odd parity. Afterwards,the oscillation of the potential energy is triggered and a periodic transition of the parity occurs as shown in Figs.3(a)–3(f). The detailed dynamics can be descripted as follows: in the nonlinear stage as shown in Fig. 3(a), the structure of the KH mode is twisted obviously due to the shear flows. From the timet=2420 tot=2450 as shown in Figs.3(a)and 3(b),the mode structure alters from the odd parity to the even parity. Correspondingly, the shear rate decreases sharply which is displayed in Fig.2(b). As the shear rate decreases to the minimum,the structure inverses oppositely to the even parity as shown in Fig.3(c). Afterwards,the symmetry is turned into the odd parity again as shown in Figs. 3(d)–3(f), which corresponds to the phase within the shear rate in Fig 2(b) increasing from the timet=2490 tot=2570. Comparing the observation above with the case imposing moderate shear flow,the symmetry breaking of the KH structure is mainly associated with the zonal flow dynamics.In other word,the oscillatory behavior results from the modification effect of the newly generated zonal flow on the equilibrium flow shear.
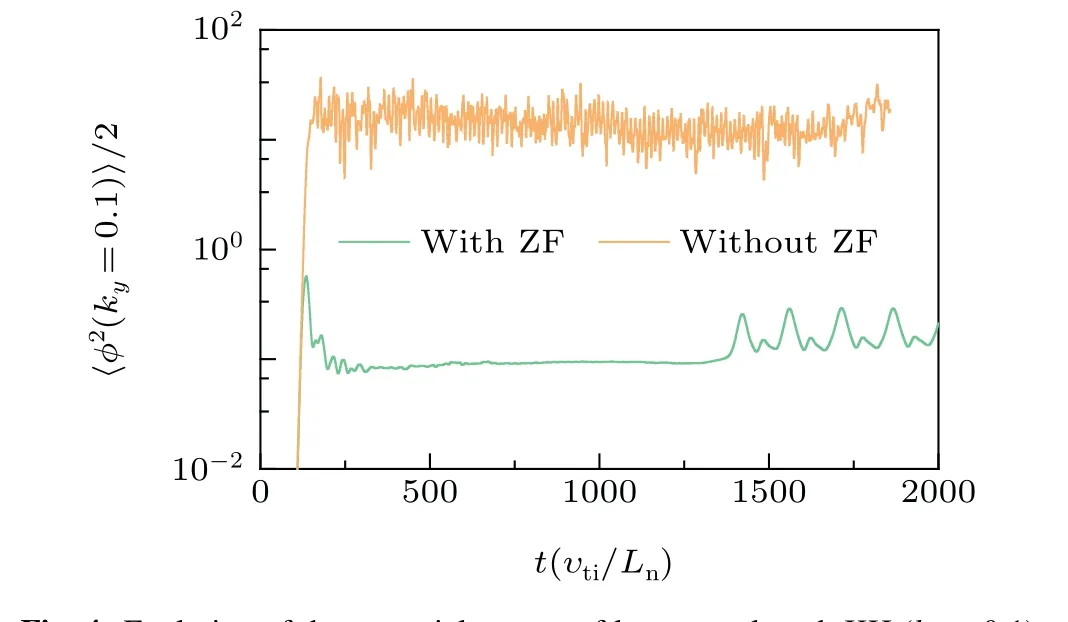
To further examine the role of the newly generated zonal flow, nonlinear simulations with/without zonal flow component are designed. As exhibited in Fig. 4, the oscillation behavior of potential energy of the KH mode disappears in the case without the zonal flow. Furthermore, the influence of the structure of zonal flow on the oscillation behavior is inspected. The kinetic energy of the newly generated zonal flow is separated according to the radial parity,as plotted in Fig.5,clearly showing that the odd-parity part displays the oscillatory feature same as the behavior of the potential energy (all modes(ky=0.1–0.9)except for the dominant ITG component(ky=0.8))as shown in Fig.1.


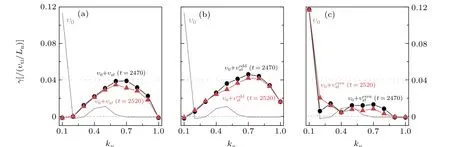
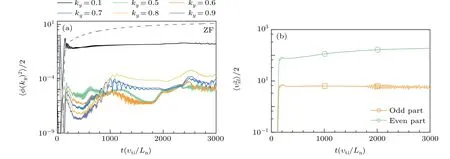
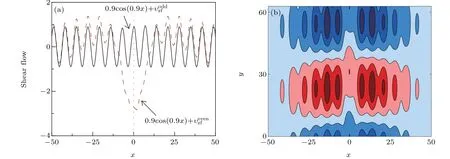
The analyses above may conclude that the oscillation behavior of the ITG fluctuations as well as the KH mode excited by imposed sinusoidal-type small-scale shear flow results from the role of the zonal flow with odd parity. However, a question may arise what happens if a cosine-type small-scale shear flow is imposed. To clarify it, a simulation similar to that in Fig.1 is performed by imposing a cosine-type shear flow,i.e.,υ0=Acos(kqx).Figure 7(a)exhibits that remarkable periodic oscillations do not appear. The kinetic energy of the newly generated zonal flow in the nonlinear phase is relatively static no matter the shear flow parity as shown in Fig.7(b). Further shown in Fig.8(a),the odd part of the zonal flow is too weak compared with the even part which plays less important role in modifying the equilibrium shear flow. More importantly,the modified flow profile is symmetry around the rational surfacex=0 in Fig. 8(a) with the even symmetry same as the mode structure of long wavelength component withky=0.1 as shown in Fig.8(b).Here,it may correspond to the unbroken symmetry of the KH mode which contributes to the generation of the zonal flow as well.
4. Turbulence transport
The role of small-scale shear flow in turbulent transport is also evaluated. Theoretically, the turbulent heat transport is mainly attributed to the electrostatic fluctuation which ignores the contribution from magnetic fluctuations. The transport coefficient is expressed as[40]χi(ky)[=-(ρi/Ln)(cTi/eB)〈˜Ti(ky)∂˜φ(ky)/∂y〉/(1+ηi)]. The evolution of turbulent heat transport corresponding to differentkymodes is illustrated in Fig.9.χiis featured with periodic intermittency which is oscillating with KH mode in the approximative phase.The transport properties observed here are interesting. It is worthwhile to further discuss whether it is driven by the KH mode or the ITG turbulence mostly.
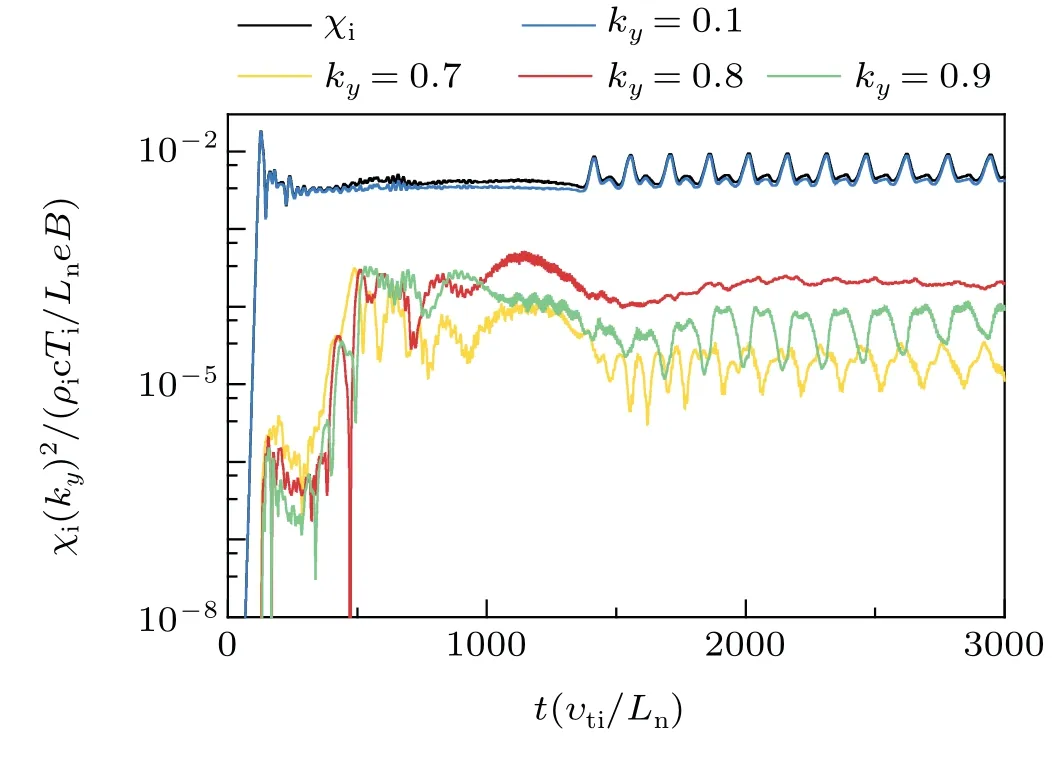
First of all, the turbulent transport with different amplitude of small-scale shear flow is compared. For the givenηi,the intermittency occurs earlier as the amplitude of the shear flow increases distinctly. In comparison d with the case without the KH mode(A=0),the dependence of the transport level corresponding to the component ofky=0.1 on the flow amplitudeAand the total turbulent transport coefficient for both relatively weaker (A=0.85) and stronger (A=0.9) KH instabilities are plotted in Fig. 10. It can be seen that the heat transport caused by the KH mode is greatly higher than that in the case withA=0 in Fig.10(a),showing that the KH mode mainly contributes to the resultant transport level. The transport level in the case withA=0.85 approaches to the level in the case without external shear flow, as shown in Fig. 10(b).However,it is enhanced visibly in the caseA=0.9. This may be ascribed to the role of the zonal flow generated nonlinearly by the KH mode,in which the effects of the KH destabilization and the zonal flow stabilization balance with each other. As a result, the complex nonlinear interaction among the EM ITG and KH modes, and the self-generated zonal flow with externally imposed small-scale shear flow make the heat transport limited.
Furthermore, another parameter,ηi, also influences the characters of the transport as shown in Fig.11. In Fig.11(b),the total heat transport is enhanced significantly whenηi>1 as the stronger ITG dominates the transport. Compared with Fig. 11(a), stronger ITG is excited which causes dominant contribution to the transport and here the KH mode may play less role in the total transport.This is different from the behavior withηi≤1 in which the KH mode contributes to almost total heat transport. It is also illustrated that whenηiincreases to a higher value, the oscillation behavior disappears in the evolution of both the instability and the heat transport.

5. Summary
In this work,it has shown that the equilibrium shear flow can excite the KH instability to interact with different scale fluctuations through direct nonlinear mode coupling and/or indirect modification of the shear flow by the zonal flow. Here,the equilibrium shear flow is characterized by small scale zonal flow, which can be created by the CTEM in tokamak plasmas. Our work above illustrates a mechanism of waveflow energy transfer process, which can be considered as another energy channel among cross-scale turbulence with shear flows. The focus is on revealing the underlying mechanism of multi-scale multi-mode nonlinear interaction. Compared with the case with moderate amplitude small-scale shear flow,not only the KH mode but also the ITG modes can become two dominant components to nonlinearly couple with each other. Interestingly, a prominent periodic oscillation of fluctuation intensity except for dominant ITG component is revealed in turbulence evolution, which onset time depends on the ion temperature gradient and the shear flow amplitudes corresponding to different KH instabilities. It is identified that the underlying mechanism results from the zonal flow dynamics, which is mainly generated by the KH mode and backreacts on it. It is demonstrated that the odd symmetric components of zonal flow(same symmetry as the external flow)make the radial parity of the KH mode alteration through adjusting the drift velocities at two sides of the resonant surface so that the KH mode becomes bursty first. Afterwards, the ITG oscillation follows due to nonlinear mode coupling among the KH mode and ITG components. Moreover,the turbulent heat transport is enhanced by the strong shear flow while it tends to oscillate with the potential energy of the KH mode. In more detail, as the shear velocity increasing, the heat transport coefficient increases which is dominant by the KH mode withηi<1. However, the ITG mode may mainly contribute to the heat transport withηi>1 and the oscillation behavior disappears in the evolution of both the instability and the heat transport.
Acknowledgments
Project supported by the National Key Research and Development Program of China (Grant Nos. 2017YFE0301200 and 2017YFE0301201), partially by the National Natural Science Foundation of China (Grant Nos. 11775069 and 11925501), and the Liaoning Revitalization Talents Program(Grant No.XLYC1802009).
Appendix A:The influence of the artificial dissipations on the oscillatory behaviors
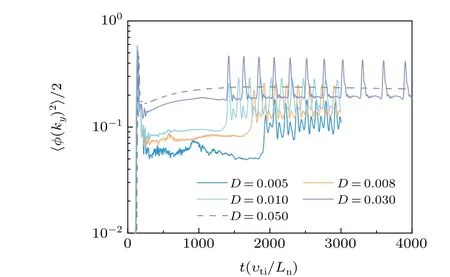
In this part, the scans of the classical cross-field dissipations on the oscillatory behaviors are exhibited. For example,as shown in the Fig. A1, the values of the dissipation determine the evolution of the KH mode. With the dissipation increasing,the intermittency occurs earlier and the amplitude of the potential energy is slightly enhanced as well. However,accompanied with the higher value of dissipations,the oscillatory behavior vanishes. Furthermore, the detailed analysis of the dissipation effect on the spectral structure will be considered in the future work.
猜你喜欢
杂志排行
Chinese Physics B的其它文章
- Switchable terahertz polarization converter based on VO2 metamaterial
- Data-driven parity-time-symmetric vector rogue wave solutions of multi-component nonlinear Schr¨odinger equation
- Neutron activation cross section data library
- Multi-phase field simulation of competitive grain growth for directional solidification
- A novel similarity measure for mining missing links in long-path networks
- Effects of electrical stress on the characteristics and defect behaviors in GaN-based near-ultraviolet light emitting diodes
