基于Newmark滑块位移法的岸坡地震稳定性简易分析方法*

高树飞，冯云芬

(聊城大学建筑工程学院，山东 聊城 252000)

地震作用下岸坡的稳定性是水运工程抗震设计的重要内容，国内外规范主要采用拟静力法和时程分析法进行抗震验算[1-2]。拟静力法将地震作用简化为土体所受的惯性力，再采用常用的土坡和地基稳定性验算方法(如圆弧滑动面法和条分法)进行稳定验算。此法概念明确、计算简便，故得到广泛应用，JTS 146—2012《水运工程抗震设计规范》[3]采用的就是该方法。但是，拟静力法无法评估地震引起的大变形对岸坡和结构的影响，国外码头抗震设计规范和标准[4-7]除了要求采用拟静力法验算岸坡稳定性以外，还要求验算岸坡的地震永久变形(自由场)是否满足限值要求，由此判定岸坡稳定性是否满足要求，以及是否需要进行详细复杂的土-结构相互作用分析，而我国规范并无相关方法。时程分析法需要建立复杂的桩-土相互作用模型，通过对模型底部输入地震动记录得到岸坡的地震反应，结果较为准确，但计算较为复杂、计算量较大，故Newmark于1965年提出将滑动坡体视为刚塑性滑块近似计算岸坡和土石坝的永久变形，即Newmark滑块位移法，被许多规范和标准所采用。

Newmark滑块位移法不再对实际的岸坡进行时程分析，而是利用地震动记录对滑块进行分析，并将滑块的位移作为岸坡的地震永久变形。由于地震动的随机性，需要使用大量地震动记录进行分析。为方便工程设计人员使用该方法，许多学者将滑块的位移结果进行统计分析后得出了相关的图表或公式，供抗震设计使用。但是，前述国外规范和标准采用的滑块位移计算图表或公式均是基于拟合于当地规范设计反应谱的人工地震动或世界各地(不包括中国)的天然地震动记录，这些地震动记录无法反映我国的地震动特性，其他学者[8-9]提出的类似公式亦是如此。虽然高树飞等基于拟合于我国水运工程抗震设计规范反应谱的人工地震波，给出了相应的滑块位移均值的计算公式，但是公式较为粗糙，未能充分反映反应谱参数的影响，更重要的是未能给出滑块位移的概率统计特性。由于均值的保证率只有50%，而随着性能化抗震设计方法的发展，结构的破坏标准可以根据业主的需求确定，因此得到更高保证率下的滑块位移计算方法以提高抗震设计的安全水平是十分必要的。

本规范设计反应谱考虑了我国地震动特性的影响，且国内天然地震动记录较少，故合成大量拟合于我国水运工程抗震设计规范反应谱的人工地震波，开展Newmark滑块位移计算，对所得位移进行统计分析，确定其均值、变异系数和统计分布，并利用回归分析提出滑块位移均值和变异系数的计算式，由此确立基于Newmark滑块位移法的岸坡地震稳定性简易分析方法，为岸坡抗震设计提供参考。

1 人工地震波的合成

合成人工地震波时需考虑地震动的不确定性，方法有很多，较常用的是三角级数法[10]，该法也被很多商业软件使用，如SeismoArtif。本文利用该软件，以JTS 146—2012《水运工程抗震设计规范》中设计反应谱为目标反应谱，见图1，图中公式为反应谱下降段的表达式。其中β为动力放大系数(自振周期为T的结构的谱加速度Sa与地面峰值加速amax的比值)，Tg为场地特征周期，与场地类别和设计地震分组有关；图中设计反应谱的阻尼比为5%。参考规范中有关设计基本加速度和特征周期的取值，反应谱参数Tg的取值为0.25、0.30、0.35、0.40、0.45、0.55、0.65、0.75、0.90 s，amax的取值为0.10g、0.15g、0.20g、0.30g、0.40g，g为重力加速。对地震波的持时td，考虑取值为10、12、14、16、18、20、24、30、36、44 s。由此，共有45个目标反应谱，对于每种持时合成8条地震波，一共合成3 600条地震波。在合成过程中，人工地震波反应谱与目标反应谱的相对误差平均值保持在10%以内。Tg=0.55 s、amax=0.30g和td=30 s时的一条人工地震波及其加速度反应谱见图2，由图2可见：人工地震波的反应谱和设计反应谱符合较好，而且该地震波也较好地体现了天然地震波强度具备的上升后保持平稳再下降的变化特点。

图1 规范中的设计反应谱

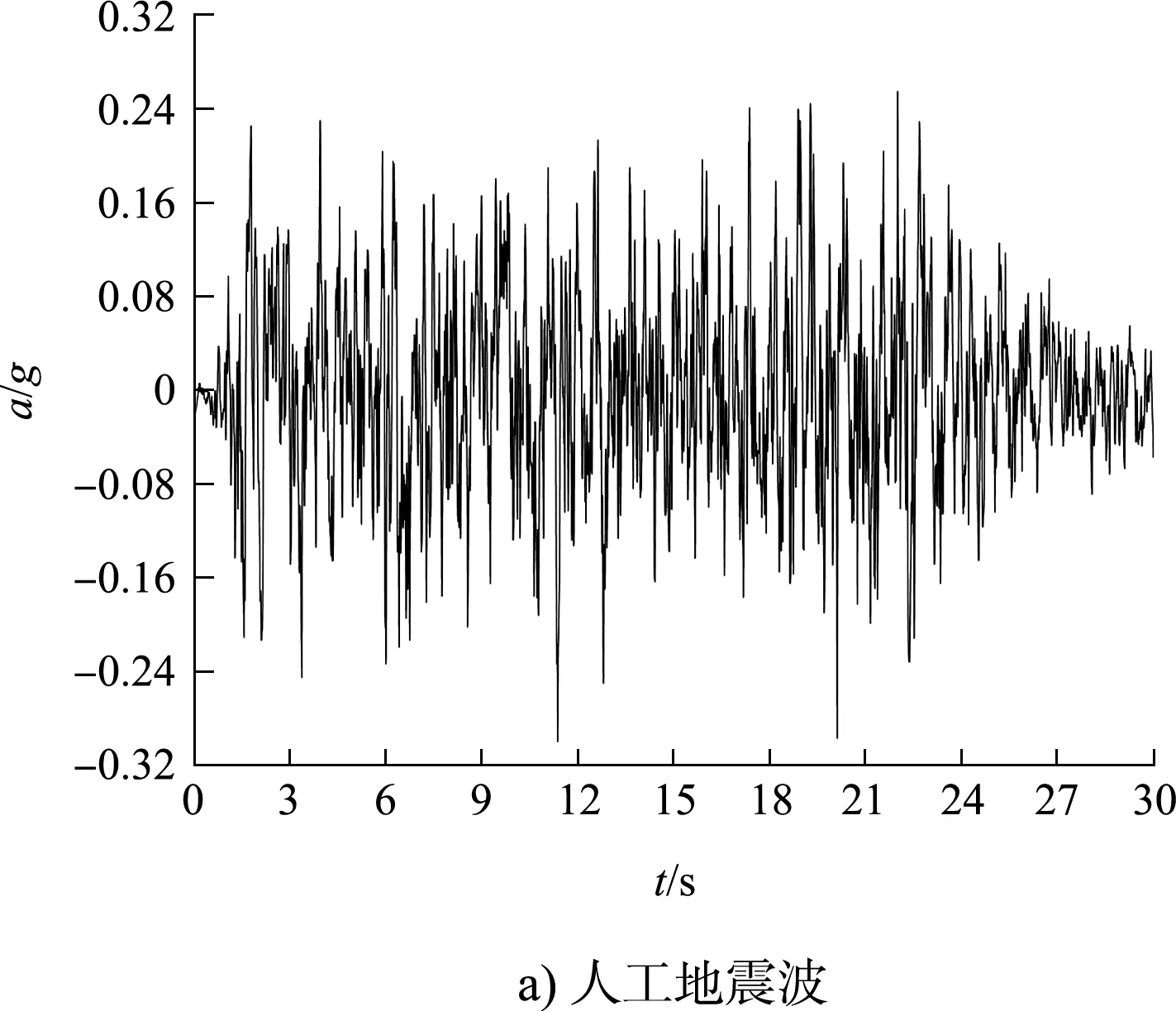
图2 人工地震波及其加速度反应谱

2 Newmark滑块位移计算与讨论

2.1 Newmark滑块位移法基本原理

Newmark滑块位移法将岸坡滑动体视为刚塑性滑块，滑块在地震波作用下，在某一时刻当加速度达到并超过一临界加速度ay时，滑块开始滑动，滑块的位移可以通过对地震动加速度时程记录进行两次积分后得到，所得滑块位移即岸坡的永久变形见图3[11]。滑块开始滑动时的临界加速度ay可称为屈服加速度，一般通过岸坡拟静力稳定分析得到，当岸坡稳定系数等于1时所施加的加速度即为ay，需通过反复迭代确定，对一些均质岸坡也有相关的简化计算公式，具体计算方法见文献[12-13]。Newmark滑块位移法相较于复杂的数值方法(如有限单元法和有限差分法)不必建立复杂动力分析模型，也不需要准确的土体参数和本构关系，而且研究表明此法对土体强度损失不大的情况准确性较高，完全可以满足工程计算的需要，特别适合需要快速估算岸坡永久变形的情况。不难看出，应用Newmark滑块位移法时，第1步需采用拟静力法确定岸坡稳定安全系数为1时的加速度，即ay；第2步需选取1组地震动记录，计算在此ay下的滑块位移。对于第2步计算滑块位移，很多规范都通过选取不同的地震记录，给出了相应的计算公式或图表，或者直接采用一些学者提出的公式。但是，这些地震动记录无法反映我国的地震动特性，故本文利用前述方法合成的人工地震波进行滑块位移计算，由此给出相应的计算公式及统计特性。

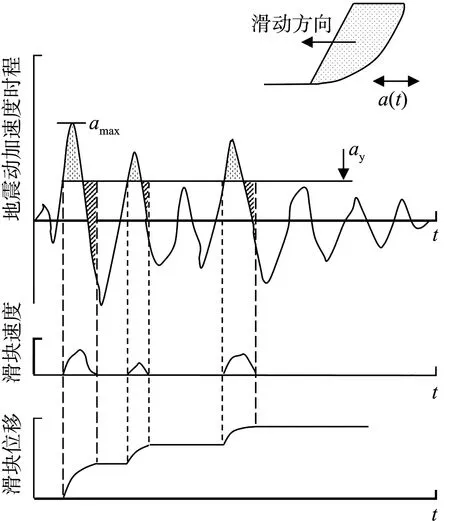
图3 Newmark 滑块位移法计算岸坡永久变形

2.2 滑块位移计算

按照2.1节所述的Newmark滑块位移法基本原理对合成的3 600条人工地震波进行滑块位移计算，计算中考虑加速度的正向和反向(即正值和负值)，则对于拟合于同一目标反应谱的80条地震动记录，在某个屈服加速度ay值下，会计算得到160个滑块位移。滑块位移分析中考虑的ay取值见表1。

表1 屈服加速度ay的取值

2.3 结果分析与讨论

2.3.1屈服加速度的影响

当amax=0.30g时，不同屈服加速度ay下滑块位移DN的变化情况见图4。图中每一条曲线(共160条)代表每条地震波在不同ay下的滑块位移的连线，图中的上限、平均和下限分别代指拟合于同一反应谱的80条人工波的DN的最大值、平均值和最小值。

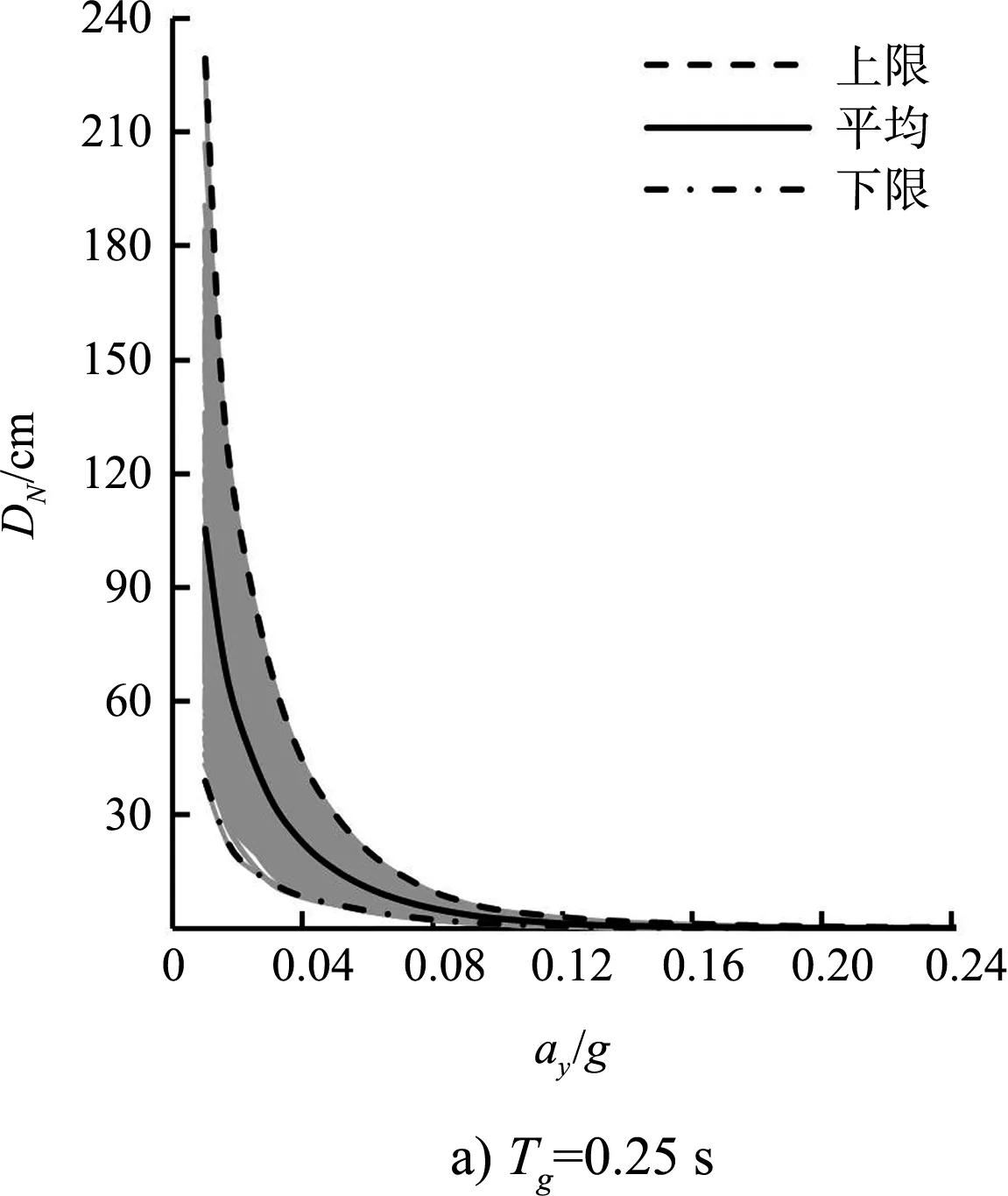
图4 滑块位移DN和屈服加速度ay的关系

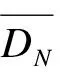
2.3.2规范反应谱特征周期的影响

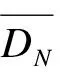
图5 滑块位移和反应谱特征周期Tg的关系

2.3.3峰值地面加速度的影响

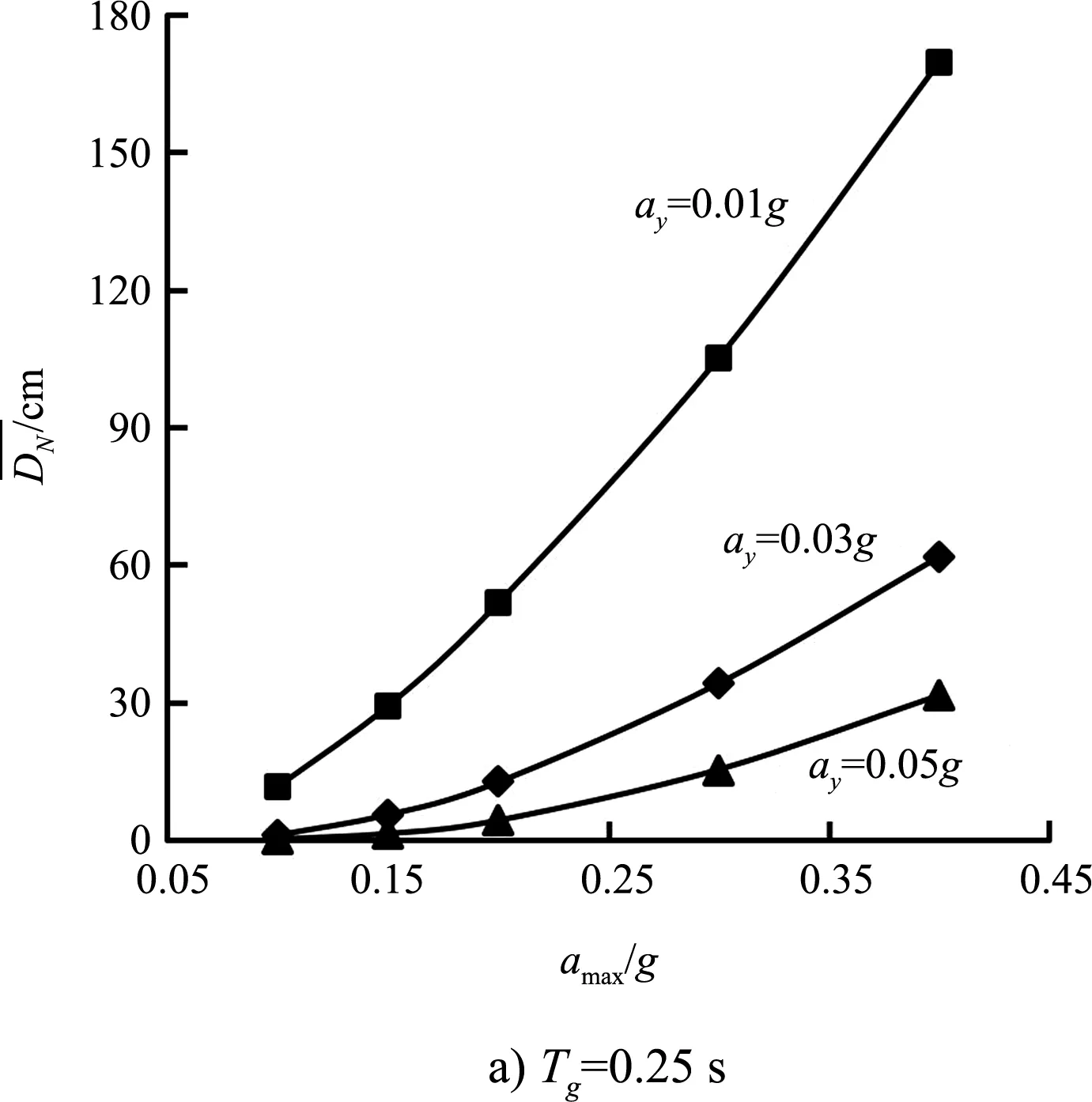
图6 滑块位移和峰值地面加速度amax的关系

3 滑块位移统计分析及稳定性验算

3.1 滑块位移的平均值

(1)

式中：λ1、λ2、λ3和λ4为参数。

lg(-λ1)=4.152+1.017Tg-8.941amax-

(2)

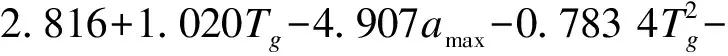
(3)

lg(-λ3)=2.072-0.046 74Tg-3.255amax-

(4)

(5)

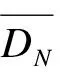
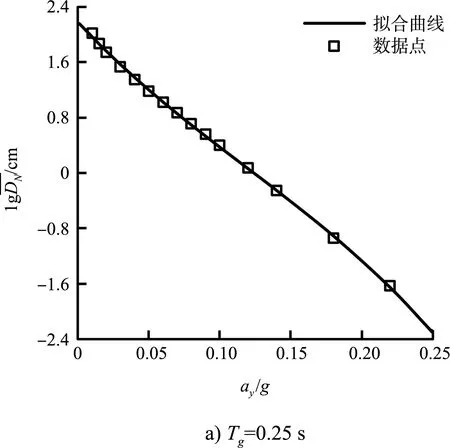
图的计算值和拟合曲线的关系

3.2 滑块位移的变异系数

对于滑块位移的变异系数δDN，在分析中同样将每组样本取为每一目标反应谱下80条人工波在同一ay下的160个滑块位移，经计算可得不同Tg和不同ay/amax下的δDN，见图8。经拟合后可得δDN的表达式：

图8 滑块位移的变异系数

(6)

式中：β1、β2、β3和β4为参数，取值见表2。鉴于场地类别和设计地震分组按照规范的划分方法确定类别以后，相应的特征周期Tg将会是一个固定值，同时考虑表中数据并无明显的规律性，因此不对表中数据进行拟合给出参数的计算表达式。

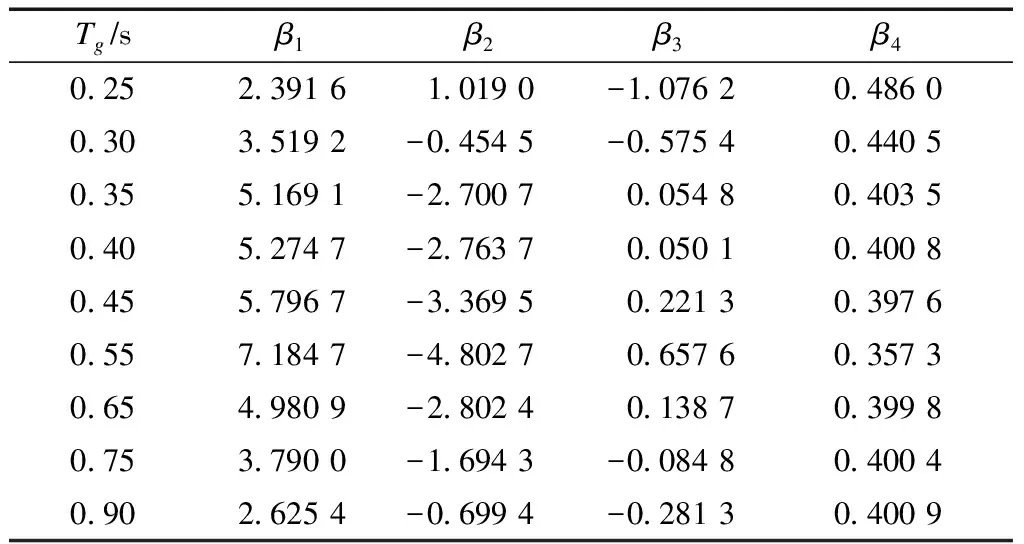
表2 参数β1、β2、β3和β4的取值

3.3 滑块位移的概率分布

为合理确定滑块位移的概率分布，amax=0.30g和ay=0.07g时不同Tg下滑块位移的频率分布见图9，图中还绘制出了根据前文所得的均值和变异系数确定的对数正态分布的概率密度曲线。由图9可见，概率密度曲线和直方图符合较好。

图9 滑块位移的频率分布直方图

为确定滑块位移是否服从对数正态分布，采用K-S检验对不同Tg、amax、ay下的滑块位移计算结果进行假设检验。考虑5种amax、9种Tg以及表1中所列的ay，共计585组样本，在显著性水平α取0.01的情况下，其中474组样本服从对数正态分布，占总数的比达81.03%，因此可认为滑块位移DN服从对数正态分布。amax=0.30g和ay=0.07g时不同Tg下滑块位移数据点的累计频率和对数正态分布函数曲线见图10，分布函数的参数则按照前文所得的平均值和变异系数确定，同时图中还绘制出了恰好拒绝原假设时的分布函数曲线，由图10可见，由本文统计参数确定的分布函数曲线处于两条拒绝原假设的函数曲线之间。

图10 滑块位移的累积频率

3.4 稳定性分析

国外码头抗震设计规范和标准将不同地震动记录的滑块位移均值作为设计依据，并确立了相应的公式或图表用于岸坡地震永久变形。在利用公式或图表计算得到岸坡永久变形值后，规范和标准均是通过将计算值同规定的限值进行对比来验算岸坡稳定性。本文建议我国岸坡地震稳定性分析也可采用上述规范和标准中的方法，鉴于不同地区的地震动特性差别较大，故建议采用本文基于拟合于我国水运工程抗震设计规范反应谱的人工地震波确定的公式(1)计算岸坡永久变形值。

对于岸坡永久变形的限值，目前国内还缺乏相关研究，建议采纳国外相关研究成果确定。文献[4-6]建议，设防地震水准在50 a内超越概率分别为50%、10%和2%时，岸坡地震永久变形限值可分别取3 in(7.62 cm)、12 in(30.48 cm)和36 in(91.44 cm)；文献[14-15]则建议，对于50 a内超越概率分别为50%、10%的地震水准，限值范围可分别取7～15 cm和15～30 cm，该建议被国际航运协会标准所采用。鉴于我国水运工程抗震设计规范采用的设防地震水准在50 a内超越概率为10%，参考上述文献，本文建议限值取为30 cm。另外，随着基于性能的码头抗震设计方法的发展[16]，业主也可基于自身的需要自行确立地震永久变形限值。

考虑到上述规范和标准中的验算方法采用均值作为设计依据，而均值的保证率只有50%，对于其他保证率α，考虑到本文确定的滑块位移概率分布，该保证率下的永久变形值DN，α可按下式计算：

(7)

其中

(8)

(9)

式中：Φ(·)为标准正态分布函数。

对于在工程设计中常用的95%的保证率，DN，95%可按下式确定：

lnDN，95%=μlnDN+1.645σlnDN

(10)

4 案例分析

某高桩码头横断面见图11，当地抗震设防烈度为9度，设计基本地震加速度amax=0.40g，场地特征周期Tg=0.45 s。按照我国水运工程抗震设计规范的规定，对岸坡进行静力稳定性分析，得到的抗力分项系数(稳定安全系数)为1.06，大于1，满足我国规范要求。按照文献[6]的要求，当岸坡拟静力稳定安全系数取值小于1.1时，需评估岸坡的地震永久变形是否满足限值要求，若不满足则须进行详细的桩-土相互作用分析。但需要注意我国规范和文献[6]在岸坡拟静力稳定分析时采用的地震系数不同，文献[6]规定地震系数取峰值地面加速度值的50%，但我国规范是在计算岸坡土条地震惯性力标准值时考虑0.25的系数，即相当于我国规范取的地震系数是峰值地面加速度值的1/4，如若按照文献[6]的地震系数取值进行稳定性分析，则稳定安全系数会更小。有关中美岸坡拟静力稳定分析的区别也可参看文献[1]。

图11 码头断面(尺寸：mm；高程：m)

5 结论

1)利用地震永久变形评价岸坡稳定性相比于拟静力稳定安全系数能更直观地反映地震的影响，永久变形值可由Newmark滑块位移法快速、简便地确定，一旦变形满足限值要求即可避免进行复杂的土-结构相互作用分析，降低了码头抗震分析的难度，可参考国外规范将岸坡拟静力稳定分析的稳定安全系数(抗力分项系数)小于1.1作为进行岸坡地震永久变形验算的条件。

2)我国规范反应谱确定的岸坡地震永久变形可表示为岸坡屈服加速度的函数，其变异系数是屈服加速度和峰值地面加速度的比值的函数，且服从对数正态分布，计算公式很好地反映了我国地震动特性。

3)对于我国的设防地震动水平，岸坡永久变形限值建议可取为30 cm，也可根据业主的需要确定相应的限值；由于均值作为设计依据时的保证率仅有50%，因此本文给出了更高保证率下的计算公式，以便在岸坡抗震分析时作为参考，以提高设计结果的安全度。