单挡板桩基透空堤的透浪系数物理模型试验*

张万威，陈国平，严士常，马洪蛟 ，谭慧明，郭寅晖

(1.海岸灾害及防护教育部重点实验室(河海大学)，江苏 南京 210098；2.河海大学 港口海岸与近海工程学院，江苏 南京 210098；3.上海滩涂海岸工程技术研究中心，上海 200061)

透空式防波堤作为一种新型的防波堤结构，与传统实体式防波堤结构相比，具有施工速度快、节省工程材料用量、有利于港域内外水体自由交换等优点。较为常见的透空式防波堤结构有：小间距直桩式透空堤、栅栏式透空堤、挡板式桩基透空堤、多层挡板式透空堤和梳式透空堤等[1]。近年来随着施工技术的成熟、对海洋环境的保护力度加大，透空式防波堤在实际工程中得到了广泛的应用。

透浪系数是透空式防波堤研究的重要内容之一，国内外学者从理论推导、物理模型试验和数值模拟3种手段进行分析研究。对于挡浪板的透浪系数研究，Ursell[2]首次研究了无限水深时挡浪板的透浪系数，给出直立薄板的精确解，但在工程实际时计算结果偏差较大，仅在较深水时有较好的符合性；Wiegel[3]利用能量传递理论，假定透射波能量等于直板下的入射波能量，在忽略波浪绕射和反射的情况下，推导求得有限水深单层挡浪板的透浪系数计算公式，其公式形式简洁、假设合理，被各国学者广泛使用；邱大洪等[4]在Wiegel公式的基础上，考虑入射波能量遇到防波堤时有绕射现象，给出挡浪板透浪系数的解析解，并使得该解在深水时与精确解相符合；Kriebel等[5]在Wiegel理论公式的基础上考虑挡浪板的反射，将反射能量计入参与透射的总能量中，按波能流守恒推导得到挡浪板的透浪系数。基于能量传递的方法较为简洁但存在一定的误差。

Liu等[6]应用边界元法计算得到有限水深倾斜薄板的反射系数和透射系数；Losada等[7]应用特征函数展开方法研究波浪斜撞击垂直薄壁的线性理论，求出透射系数和反射系数的理论解。特征函数展开法适用于数值模型的计算且与能量法所得的结果相差不大，但计算过程相对较为复杂，无法简便地运用于工程计算。

对于挡板式桩基透空堤，我国现行的《防波堤与护岸设计规范》[8]采用前苏联科学家拉帕教授所推导的公式，并明确了适用的条件；殷福安[9]采用理论推导和物理模型试验的方法对挡板式透空堤透浪特性进行研究，并给出透浪系数计算的理论公式；王伟[10]采用系列物理模型试验研究不规则波作用下单挡浪板在无越浪、越浪以及有水平板等3种情况下的透浪特性，并分别给出3种情况下的透浪系数计算公式；邵杰等[11]通过物理模型试验分析不规则波作用下入射波高、波周期、挡板相对入水深度、相对堤宽、相对挡板超高、相对面板超高等因素对垂直挡板式透空堤透浪系数的影响规律，并在Wiegel公式的基础上拟合了垂直挡板式透空堤透浪系数的计算公式。但是以上的研究针对的结构形式较简单，考虑的情况较有限，实际工程中结构形式的多样性和自然条件的复杂性使许多研究成果尚未得到应用。本文依托实际工程，对桩基挡板式透空堤的消浪特性开展物理模型试验研究，优化堤型结构，并将前人的研究成果进行应用，为工程设计提供参考。

1 物理模型设计

试验在波浪水槽(长80 m、宽1.0、深1.5 m)内进行，水槽首端安装不规则造波机，末端设置消波系统，水槽纵向分为两部分，宽度均为0.5 m，外侧用于铺设试验断面，内侧用于消除波浪的二次反射。造波机可按要求模拟规则波和各种谱型的不规则波。试验遵循《水运工程模拟试验技术规范》[12]，采用正态比尺，主要考虑因素为重力相似，综合考虑确定模型几何比尺为1:30。透空堤的物理模型按照比尺使用有机玻璃制作，模型见图1。桩基采用φ40 mm有机玻璃管，每榀排架2对斜桩，斜率均4:1，排架间距为0.17 m。上部结构由现浇横梁、纵向梁及现浇面板组成，在海侧的前两排纵梁间设置现浇面板，其上设置防浪墙，其他纵梁间不设面板，防波堤前侧设防浪板。根据试验要求，测试堤后波浪，分别在距离防波堤后沿0.33、1.00、1.67、2.33、3.33 m(相当于原型的10、30、50、70、100 m)的位置布置波高仪，模型平面布置及波高仪布置见图2。

图1 透空堤的物理模型

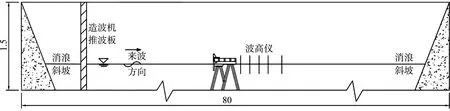
图2 模型平面布置及波高仪布置(单位：m)

该试验共有3个断面需要进行设计优化，断面1见图3，各断面优化调整情况和试验组次见表1、2。特别说明，各断面及其优化断面仅泥面高程、堤顶高程、挡浪板底高程有区别，其他断面结构形式均一致。为保证试验的可靠性，试验时每种工况重复3次，取3次测量数据的平均值为最终结果。本文所呈现的试验数据结果均是通过试验测量值乘以模型比尺因子换算得到的原型值。

图3 断面1(高程：m；尺寸：mm)

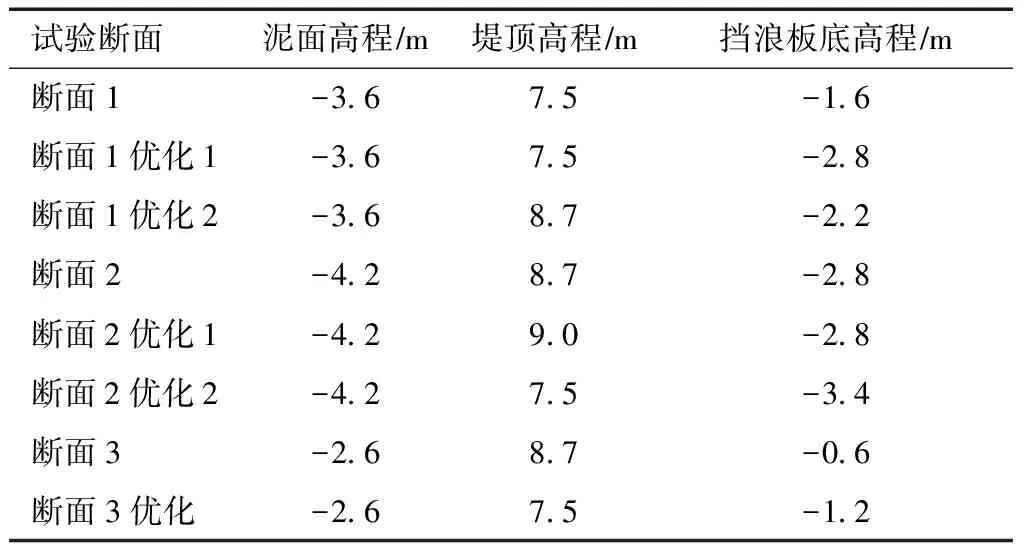
表1 各断面优化调整情况

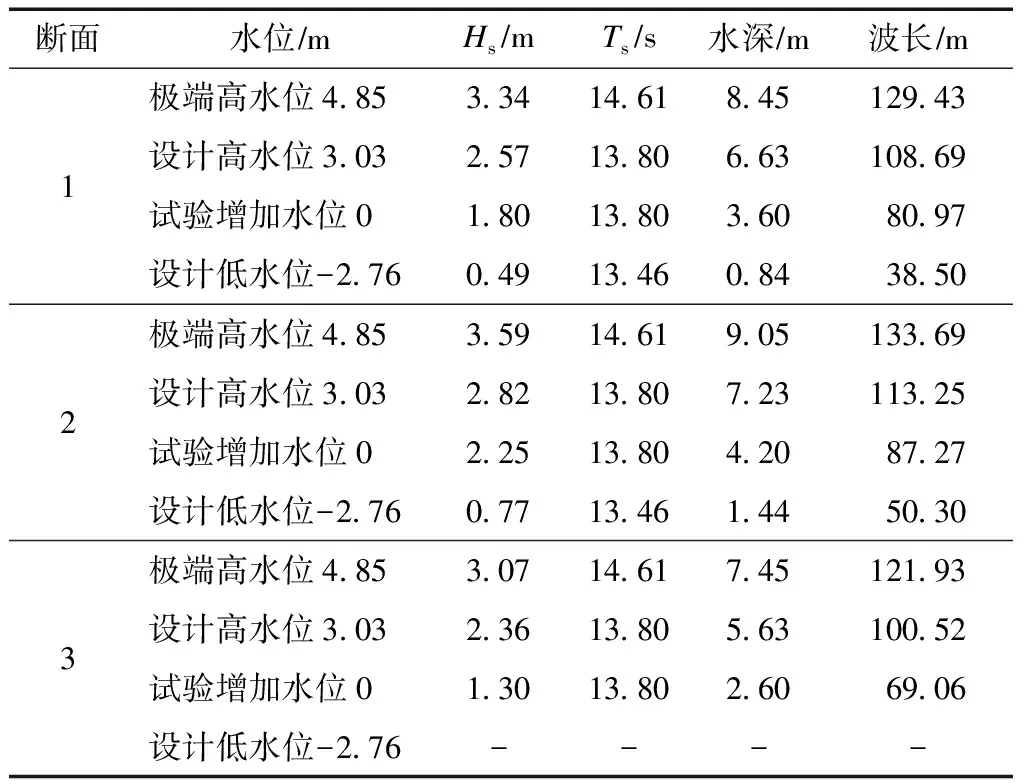
表2 试验组合

2 试验结果及分析

透浪系数Kt反映了防波堤的消浪能力，其物理含义为堤后透射波高与堤前入射波高之比。堤前入射波高在无堤时事先率定，堤后透射波高需要由堤后摆放的5根波高仪测量得到的数值确定。3个断面及其优化断面堤后波高变化见图4～6。可以看出，极端高水位时各断面的最大波高出现在堤后10 m处的波高测点，这是由于越浪水体下砸形成的局部水体跳动导致的，目前对透空堤透浪系数的研究极少考虑堤顶越浪的影响，各家公式也很少考虑堤顶越浪这个因素，然而对于受越浪影响较大的防波堤，堤后透射系数与堤顶越浪和堤底透浪有关[13]，所以有必要在计算时考虑堤顶越浪这个因素。由图4d)可以看出，各断面的堤后波高沿程降低，这是因为在设计低水位，水深较小，波高与水深之比γ=0.58，大于不规则波在浅水区波浪破碎时的指标γb=0.55，故波浪发生破碎引起波高沿程逐渐减小，这种情况在本文中不计算其透浪系数。其他情况下，堤后各测点波高沿程变化并不大，仅堤后10和30 m测点的波高由于水面壅高、波浪形态紊乱等原因有波动，将堤后较为稳定的50、70、100 m点的波高取平均值作为透射波高。

图4 断面1及其优化断面堤后波高变化

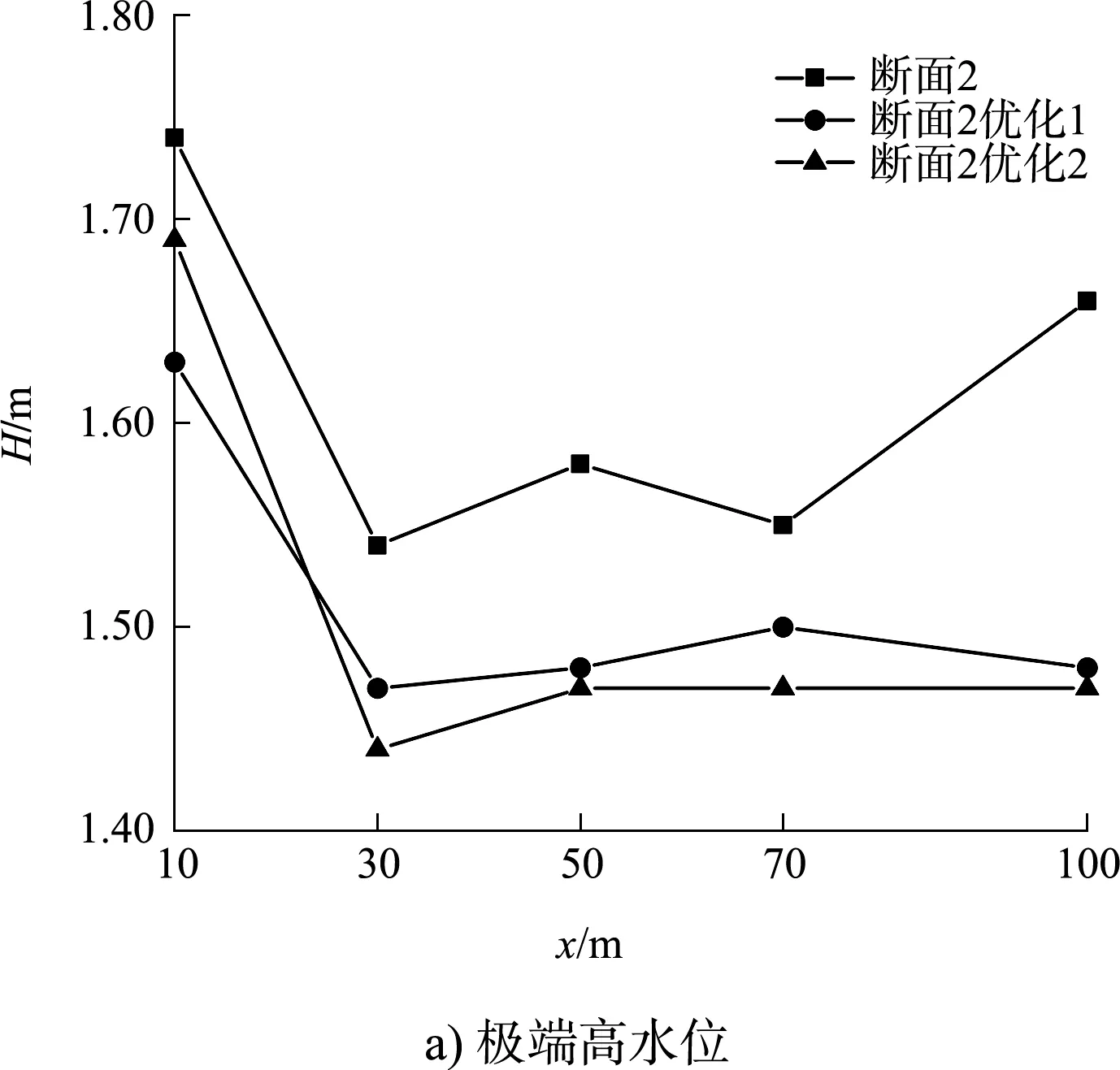
图5 断面2及其优化断面堤后波高变化

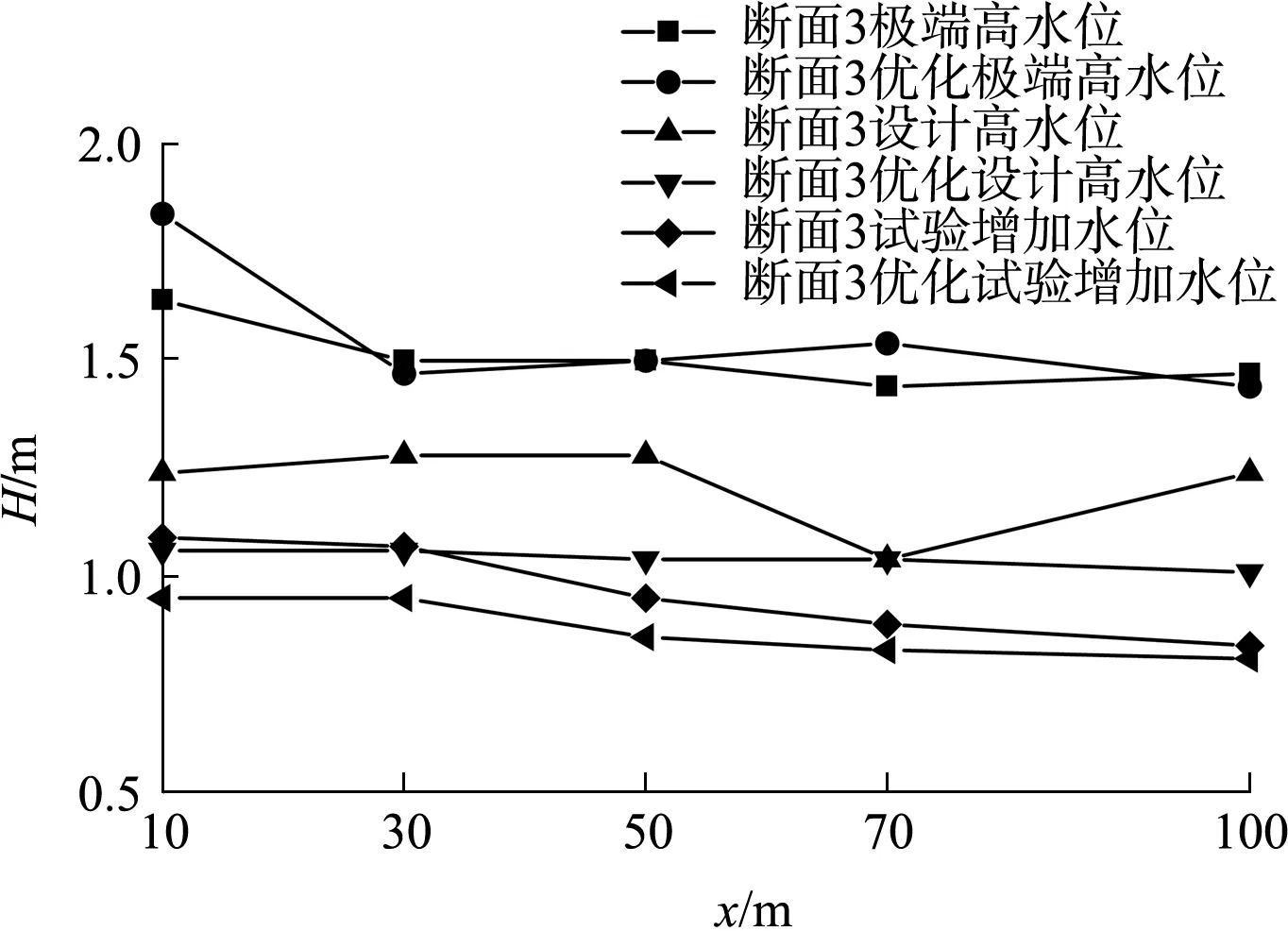
图6 断面3及其优化断面堤后波高变化

各断面的透浪系数见表3。结合图4～6可知，断面1优化1与断面1相比，在保持堤顶高程一致的情况下，将挡浪板高程从-1.6 m调整为-2.8 m，各水位下的断面透浪系数大幅下降，平均下降幅度为28.1%，断面1优化2与断面1相比，将堤顶高程从7.5 m调整为8.7 m的同时将挡浪板高程从-1.6 m调整为-2.2 m，各水位下的断面透浪系数有所下降，平均下降幅度为15.9%，断面1优化2虽然通过增加堤顶高程减少了越浪量，但是各水位下的挡浪板入水深度不如断面1优化1，部分没有越过堤顶的水体随水面壅高回落后，透过挡浪板底部与泥面的空隙到达堤后，这说明挡浪板入水深度对桩基透空式防波堤起着关键作用[14]。由图7可知，断面1及其优化断面的透浪系数随着挡板相对入水深度t/d(t为挡浪板入水深度；d为堤前水深)增加而减小。

图7 断面1及其优化断面透浪系数随相对入水深度变化

表3 各断面的透浪系数

断面2优化1与断面2相比，在保持挡浪板底高程不变时，将堤顶高程从8.7 m调整为9.0 m，透浪系数仅在有明显越浪的极端高水位下降7%，其他水位的透浪系数基本没变；断面2优化2与原断面和优化1相比，挡浪板底高程从-2.8 m下降到-3.4 m的同时，将堤顶高程下降到7.5 m，透浪系数平均下降幅度为-8.8%，尤其在设计高水位和增加水位时下降明显，这与前文一致。

断面3优化在断面3的基础上，将堤顶高程从8.7 m调整为7.5 m的同时将挡浪板底高程从-0.6 m调整为-1.2 m，这样的优化调整使该断面的消浪特性得到增强。对桩基挡板式透空堤进行设计优化时，可以通过增加挡浪板的入水深度或增加堤顶高程或两者同时调整等方式增强其消浪特性，这需要结合工程实际情况综合考虑。

3 试验值与经验公式计算值比较

该工程的断面结构新颖且复杂，采用在海侧前两排纵梁间设置现浇面板，其上设置防浪墙，其他纵梁间不设面板的结构形式，不同于以往各家提出的公式时所针对的结构形式，故选取多个有代表性的经验公式进行计算，探讨各家公式对本文结构形式的适用性。

Wiege提出的公式如下：

(1)

式中：k为波数；t为挡浪板入水深度；d为堤前水深。

Kriebel等提出的公式如下：

(2)

(3)

《防波堤与护岸设计规范》推荐的公式如下：

(4)

(5)

式中：H1%为不规则波1%累积率波高；L为不规则波有效波长。

殷福安提出的公式如下：

(6)

式中：D为挡浪板宽度与挡板间距之和；b为桩基的宽度；ΔD为挡浪板间距。

王伟提出的公式如下：

(7)

(8)

(9)

式中：Hs为不规则波有效波高；L为不规则波有效波长；B为面板在入射波方向上的宽度；Δh为结构顶部至静水面的距离；ht为面板底部至静水面的距离。

邵杰提出的公式如下：

(10)

采用本次试验与王伟的试验数据作为原始数据，Kt试验值与各家经验公式计算值比较见图8，平均误差和相关系数见表4。可以看出，对于本文的单挡板桩基透空堤结构，Wiegel公式吻合最好，平均误差为12.03%，相关系数为0.934，虽然其形式简单但是拟合效果好，适用性广，是基于一些限制性假设的第一近似解。在本试验中，仅在断面2、断面2优化1设计低水位时，计算值较试验值偏大，这是因为该情况挡浪板入水深度较小，其消浪作用也较小，推荐使用该公式进行单挡板桩基透空堤透浪系数的估算。殷福安公式在Wiegel公式的基础上考虑了桩基的作用，计算值整体比试验值偏小一些，平均误差为16.66%，在t/d较小时(例如断面2、断面2优化1在设计低水位的情况)，必须将桩基的消浪作用考虑进来，此时推荐使用该公式进行计算。

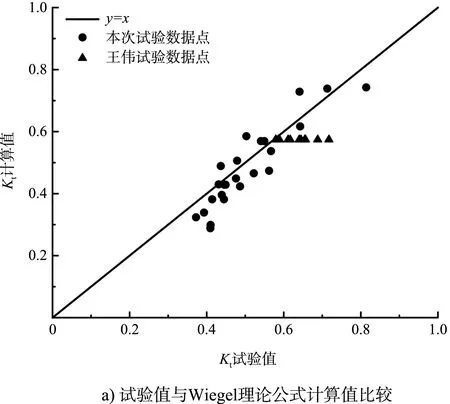
图8 试验值与各家经验公式计算值比较

表4 各家公式计算值与试验值的平均误差和相关系数

虽然只有王伟和邵杰这两个公式考虑了堤顶越浪的情况，但两个公式的计算值与试验值相比，平均误差为43%，误差非常大。这是因为两个公式建议d/L取值范围为0.11～0.50，而本文的d/L均小于0.07，不在两个公式的适用范围之内，且两者得出公式的断面结构没有挡浪墙和桩基。规范公式和Kriebel公式计算值整体都比试验值小，平均误差在25%左右，这是因为规范推荐的公式是基于双侧挡浪板透空堤的规则波试验研究得到的结果，与本文情况有较大的差别，且不满足规范的要求：当透空堤采用单侧挡浪结构时堤宽与波长之比不宜小于0.25，挡浪板入水深度与水深之比宜取0.3～0.5。Kriebel公式虽然考虑了波浪的反射，但是本文的波浪周期较长，长波的透射作用较强，导致计算值偏小。

图8还标注了王伟的部分试验数据。可以看出，尽管Wiegel公式吻合得较好，但是其公式中仅考虑了波数k、水深d、挡板入水深度t，堤顶越浪、结构超高、面板宽度等因素没有考虑入内，出现了图8a)～d)中不同的结构超高但计算得到的透浪系数一致的情况，关于复杂结构形式的挡板式桩基透空堤透浪系数有待做进一步的深入研究。

4 结论

1)试验表明，堤顶越浪对堤后波高沿程分布有影响。对于受越浪影响较大的防波堤，堤后透射系数与堤顶越浪和堤底透浪有关，有必要在计算时考虑堤顶越浪这个因素。

2)对桩基挡板式透空堤进行设计优化时，可以通过增加挡浪板的入水深度或增加堤顶高程或两者同时调整等方式增强其消浪特性，其中透浪系数随着挡板相对入水深度t/d增加而减小，增加挡浪板的入水深度能够大幅度降低透浪系数，在挡浪板入水深度相同时，增加堤顶的高程使得堤顶越浪减少，进而透浪系数下降，但下降幅度不大且仅存在于有明显堤顶越浪的水位。

3)针对本文类似的断面结构，用Wiegel、Kriebel、规范、殷福安、王伟和邵杰公式与试验结果进行对比，发现Wiegel公式吻合最好，推荐使用该公式进行单挡板桩基透空堤透浪系数的估算。

4)各家公式有各自的适用条件且针对的结构形式较简单，运用到实际工程中存在误差，需要分析不同工程所处的环境特点及结构设计特点，合理选择公式进行计算，关于复杂结构形式的挡板式桩基透空堤透浪系数有待进一步深入研究，在优化设计时须结合物理模型试验确定透空堤的透浪系数。