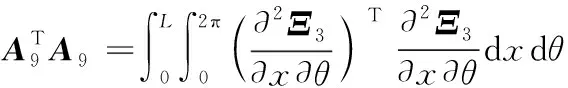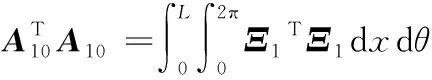一般边界条件下受轴向冲击圆柱壳的动力特性计算分析

桂夷斐， 辛绍杰， 马建敏

(1.上海电机学院 机械学院，上海 201306； 2.复旦大学 航空航天系，上海 200433)

在许多工程领域，圆柱壳结构被广泛使用，对用于结构防撞安全及各类变形吸能装置的圆柱壳，其受冲击作用下的动力屈曲一直是研究的热点问题之一。对于经典边界圆柱壳的冲击问题，许多学者在理论建模、计算方法和试验研究等方面做了大量工作。Yamaki等[1-3]基于Donnell壳理论并忽略前屈曲，对于受轴向压缩的圆柱壳得到了很多精确解。几种不同支承条件下圆柱壳的屈曲特点也被许多学者讨论[4-5]。Xu等[6-8]考虑到应力波的传播作用，对圆柱壳的动态屈曲进行了研究。Karagiozova等[9-10]基于初始缺陷的假设对圆柱壳使用离散模型进行数值模拟分析，得到了一些结论。Han等[11]基于能量关系，应用功率原理对弹性圆柱壳在刚体块轴向冲击下的动力屈曲问题进行了讨论，得到了一些关于临界速度的结论。桂夷斐等[12-14]采用应力波传播理论对不同边界条件以及不同结构类型圆柱壳的动力屈曲进行了研究。

前人对圆柱壳结构的研究集中考虑了经典边界条件的组合，事实上，边界条件作为影响结构动力特性的重要因素，研究中有必要探究弹性边界约束对受轴向冲击圆柱壳动力特性的影响。Mofakhami[15]等提出了一种在不同边界条件下，适用于多种有限长度的圆柱结构如棒材、空心圆柱和弧形板等的半解析方法，该方法中一些边界条件使用正交化方法近似满足。一些学者采用波传播方法[16-19]来预测具有不同边界条件的有限长度圆柱壳的特性。Li等[20-21]提出了一种修正的傅里叶级数法，用于任意弹性支承梁板的动力分析。Fok等[22]用能量法分析了嵌在弹性介质中的长圆柱壳的屈曲问题。Gui等[23]基于能量守恒原理，采用波动分析法讨论了轴向弹簧阻尼连接圆柱壳受冲击的动力屈曲问题。

本文根据Love薄壳理论得到圆柱壳应力应变关系，并采用一种改进的Fourier级数方法表示圆柱壳沿坐标轴方向的位移。采用基于Hamilton方程的一阶变分法对能量表达式进行推导和变换，得到受轴向冲击圆柱壳的自然频率以及屈曲临界载荷的判别式。算例中设置不同的边界刚度模拟一般边界条件，计算分析了一般边界条件对受轴向冲击的圆柱壳自然频率以及屈曲临界载荷的影响，以及不同边界条件圆柱壳屈曲模态的类型特点。

1 模型描述

如图1所示为一般边界条件下受轴向冲击的圆柱壳，定义了柱坐标系(x,θ,z)，x,θ,z分别为轴向、周向和径向坐标，u,v,w分别为圆柱壳中面的点沿x,θ,z轴方向的位移。圆柱壳长为L，壁厚为h，中面半径为R，密度为ρ，弹性模量为E，泊松比为μ。kx,kθ,kz和Kz分别为施加于圆柱壳左端(x=L处)x,θ,z方向的线性弹簧和z方向的旋转弹簧，且沿圆柱壳中面均匀分布。将弹簧刚度设置为不同的数值，则可模拟一般边界条件。

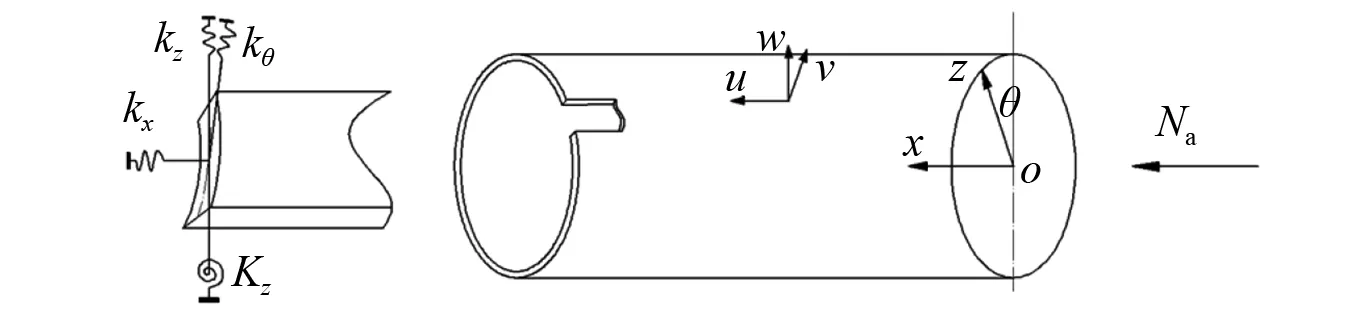
图1 圆柱壳模型及其边界条件Fig.1 Modeling of the shell and its boundary conditions

圆柱壳的应力应变关系根据Hooke定律可表示为

(1)

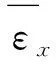
(2)

圆柱壳变形过程中面上点的应变分量可表示为

(3)

圆柱壳变形过程曲面曲率分量可表示为

(4)

式中，θx,θθ分别为沿θ,x轴的转角。

(5)

对一般边界条件下受轴向冲击圆柱壳进行能量分析时，考虑到圆柱壳变形过程中的应力和应变，需要构造可行的位移函数表示圆柱壳变形过程中的位移u,v,w。

2 位移函数表达式

考虑到3个方向的位移u,v,w在圆柱壳周向是以2π为周期的函数，因此可以用Fourier级数表示位移函数。一般边界条件下受轴向冲击圆柱壳的位移u,v,w采用如式(6)所示的改进Fourier级数的形式[24]，表示成圆柱壳轴向模态和周向模态相乘，且加上补充函数的形式。

(6)

式中：λm=mπ/L；m,n分别为圆柱壳模态的轴向和周向波数；n=0为圆柱壳轴对称模态的波数；位移函数取不同的轴向波数m和周向波数n，可展开成不同阶模态的圆柱壳位移；Amn,an,bn,Bmn,cn,dn,Cmn,en,fn,gn,hn分别为3个方向位移展开式的系数。

式(6)可写成如下形式

u=[cosλ0xcos 0θ, cosλ1xcos 0θ,

…,cosλMxcos 0θ,ξ1cos 0θ,ξ2cos 0θ,

…,cosλ0xcosNθ,…,cosλMxcosNθ,

ξ1cosNθ,ξ2cosNθ]U=Ξ1U
v=[cosλ0xsin 0θ, cosλ1xsin 0θ,

…,cosλMxsin 0θ,ξ1sin 0θ,ξ2sin 0θ,

…,cosλ0xsinNθ,…,cosλMxsinNθ,

ξ1sinNθ,ξ2sinNθ]V=Ξ2V
w=[cosλ0xcos 0θ, cosλ1xcos 0θ,

…,cosλMxcos 0θ,η1cos 0θ,

η2cos 0θ,η3cos 0θ,η4cos 0θ,

…,cosλ0xcosNθ,…,cosλMxcosNθ,

η1cosNθ,η2cosNθ,η3cosNθ,

η4cosNθ]W=Ξ3W

(7)

其中

(8)

ξ1,ξ2,η1,η2,η3,η4为构造的辅助函数；ξ1,ξ2为轴向和周向位移的补充函数；η1,η2,η3,η4为径向位移的补充函数，形式如下

(9)

(10)

构造如式(9)、式(10)所示的辅助函数并将其引入到Fourier级数的目的是，消除位移函数在圆柱壳边界上空间导数的不连续性，即确保一般边界条件下，边界力和力矩的连续性。接下来将圆柱壳应力应变以及位移代入能量表达式，并采用基于Hamilton方程的一阶变分法对能量表达式进行处理。

3 能量原理及推导变换过程

采用基于Hamilton方程的一阶变分法对圆柱壳进行分析。4个方向边界弹簧约束下受轴向冲击圆柱壳的总能量可写成如下形式

Π=T-(Um+Ub+Ua+Ω)

(11)

圆柱壳中面应变能表达式为

(12)

其中中面上点的应变分量εx,εθ,εxθ如式(3)所示。圆柱壳弯曲应变能表达式为

(13)

其中曲面曲率分量χx,χθ,χxθ如式(4)所示。圆柱壳轴向应变能表达式为

(14)

式中，Na为圆柱壳所受轴向冲击载荷。动能表达式为

(15)

储存于边界弹簧中的弹性势能表达式为

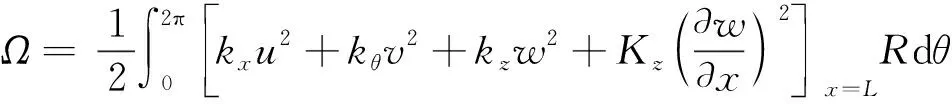
(16)

式中：C=Eh/(1-μ2);D=Eh3/12(1-μ2)。

将式(12)～式(16)代入式(11)可得

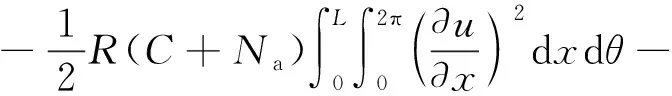
(17)

将式(7)代入式(17)进一步整理得到矩阵形式的表达式

(18)

且

X=[U,V,W]T

(19)

(20)

(21)

(22)

矩阵的详细表达式见附录A。

基于Hamilton变分原理的表达式如下

(23)

将式(18)代入式(23)，采用一阶变分法，可以给出关于式(23)的矩阵形式如下

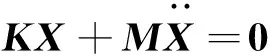
(24)

式(24)所对应的广义特征值问题可以表示为

|K-ω2M|=0

(25)

由方程式(25)可解得一般边界条件下受轴向冲击圆柱壳的自然频率以及发生屈曲的临界载荷，利用计算软件MATLAB对方程式(25)进行编程计算，对自然频率ω以及临界载荷Na进行讨论。其中隐含在方程式(25)中的轴向波数m、周向波数n、轴向边界刚度kx、周向边界刚度kθ、径向边界刚度kz、径向旋转边界刚度Kz、轴向冲击载荷Na、自然频率ω等变量的关系见附录B。

4 数值计算结果及分析

分析圆柱壳受轴向冲击时，设置不同的边界刚度模拟一般边界条件，进而分析一般边界条件对圆柱壳动力屈曲的影响，并且对一般边界条件下圆柱壳受轴向冲击的自然频率进行了讨论，本文的结果通过计算软件MATLAB编程获得。相对于壳体刚度数值1×108，无限大的边界刚度用一个极大的数值1×1012表示。取圆柱壳参数L=0.4 m,ρ=2 700 kg/m3,E=70 GPa,μ=0.33。

4.1 一般边界条件对受轴向冲击圆柱壳自然频率的影响

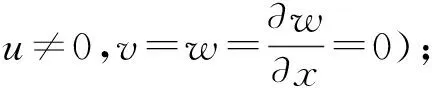
图2(a)所示为在非冲击端设置其他3个方向边界刚度无穷大，仅改变轴向边界刚度kx时，受轴向冲击圆柱壳的自然频率ω随轴向边界刚度kx的变化。图2(b)所示为在非冲击端设置其他3个方向边界刚度无穷大，仅改变周向边界刚度kθ时，受轴向冲击圆柱壳的自然频率ω随周向边界刚度kθ的变化。图2(c)所示为在非冲击端设置其他3个方向边界刚度无穷大，仅改变径向边界刚度kz时，受轴向冲击圆柱壳的自然频率ω随径向边界刚度kz的变化。图2(d)所示为在非冲击端设置其他3个方向边界刚度无穷大，仅改变径向旋转边界刚度Kz时，受轴向冲击圆柱壳的自然频率ω随径向旋转边界刚度Kz的变化。从图2(a)～图2(d)都可以看出，在边界刚度一定时，随着轴向波数m增加，自然频率ω增大。即4种不同边界条件下，轴向波数越高，圆柱壳自然频率越高。

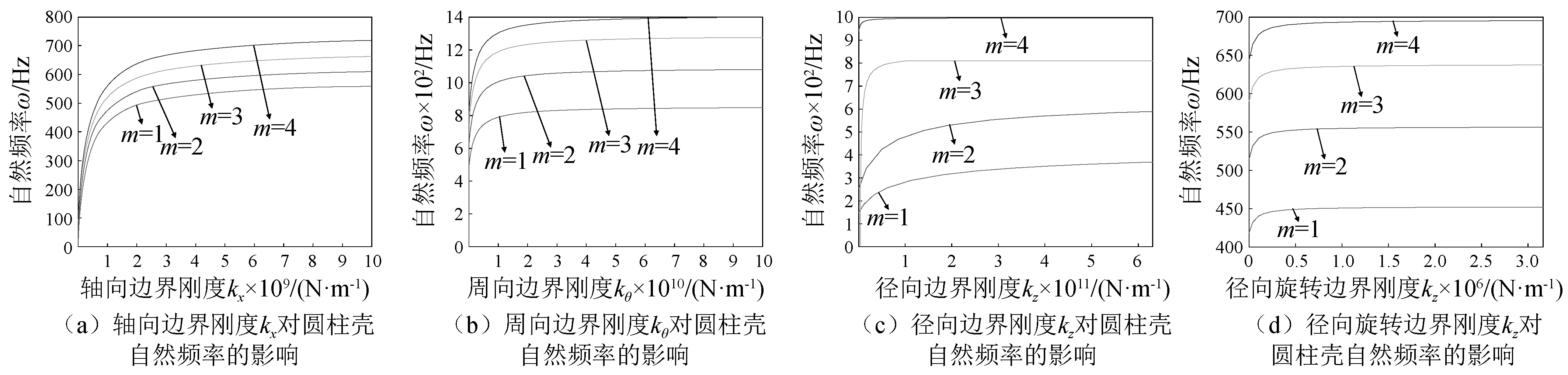
图2 圆柱壳自然频率随边界刚度的变化Fig.2 Variation of natural frequency versus boundary stiffness

图2(b)、图2(d)中随着轴向波数m增大，各阶自然频率曲线间隔越来越小，说明圆柱壳在周向边界刚度kθ或径向旋转边界刚度kz一定的情况下，随着轴向波数m的增大，相邻两轴向波数对应的自然频率变化量越来越小。

将图2(a)～图2(d)曲线都可分为敏感区域和非敏感区域，在敏感区域壳体自然频率随刚度系数增大快速增大，在非敏感区域自然频率随刚度系数增大缓慢增大，直至稳定不变。轴向、周向、径向和径向旋转各方向刚度系数较小时为敏感区域，较大时为非敏感区域。说明各方向的边界刚度系数越小，圆柱壳的自然频率越低。

图2(c)中各阶自然频率敏感区域范围随着轴向波数m增大而减小，说明在敏感区域，轴向波数越大，圆柱壳的自然频率随径向边界刚度kz变化越迅速。且圆柱壳的自然频率关于4个方向边界刚度的敏感区域不同。

图3根据式(25)，在4种不同的边界条件下，通过改变轴向冲击载荷Na、轴向波数m、周向波数n，分析圆柱壳的自然频率ω的变化规律。计算中分别只保留轴向(kx=1×104N/m，kθ=kz=kz=∞)、周向(kθ=1×104N/m，kx=kz=Kz=∞)、径向(k=1×104N/m，kx=kθ=Kz=∞)和径向旋转(Kz=1×104N/m，kx=kθ=kz=∞)的单一弹性约束，取h=0.002 m,r=0.04 m。

图3所示为受轴向冲击的情况下，在圆柱壳的非冲击端依次设置为仅保留轴向弹性约束、周向弹性约束、径向弹性约束、径向旋转弹性约束时，自然频率ω随轴向冲击载荷Na的变化关系。在4种不同边界条件下都可看出，轴向波数m和周向波数n一定时，自然频率ω随着轴向冲击载荷Na增大而降低，当自然频率ω接近零时，轴向冲击载荷Na接近临界载荷。且随着周向波数n增大屈曲临界载荷增大，自然频率ω及屈曲临界载荷都随着轴向波数m的增大而增大。

对比图3，4种不同边界条件下自然频率随轴向冲击载荷的变化量可知，图3(a)和图3(d)的自然频率变化量差别不大，图3(b)和图3(c)的自然频率变化量差别不大，且图3(b)、图3(c)的自然频率变化量比图3(a)、图3(d)的大。

4.2 一般边界条件对圆柱壳临界载荷的影响

图4根据式(25)，分析圆柱壳的屈曲临界载荷Na随边界刚度、轴向波数m、圆柱壳厚径比(h/R)的变化规律，此时圆柱壳自然频率ω=0，周向波数n=1。接下来的计算中依次将圆柱壳设置为仅保留轴向弹性约束、周向弹性约束、径向弹性约束、径向旋转弹性约束的情形，表示4种不同的边界情况。仅保留轴向弹性约束时设置边界条件为kθ=kz=Kz=∞(即x=L处，u≠0,v=w=∂w/∂x=0)；仅保留周向弹性约束时设置边界条件为kx=kz=K=∞(即x=L处，ω≠0,u=v=∂w/∂x=0)；仅保留径向弹性约束时设置边界条件为kx=kθ=kz=∞(即x=L处，w≠0,u=v=∂w/∂x=0)；仅保留径向旋转弹性约束时设置边界条件为kx=kθ=kz=∞(即x=L处，∂w/∂x=≠0,u=v=w=0)。

图4(a)所示为在非冲击端设置其他3个方向边界刚度无穷大，仅改变轴向边界刚度kx时，受轴向冲击圆柱壳的屈曲临界载荷Na随轴向边界刚度kx的变化曲线。图4(b)所示为在非冲击端设置其他3个方向边界刚度无穷大，仅改变周向边界刚度kθ时，受轴向冲击圆柱壳的屈曲临界载荷Na随周向边界刚度kθ的变化曲线。图4(c)所示为在非冲击端设置其他3个方向边界刚度无穷大，仅改变径向边界刚度kz时，受轴向冲击圆柱壳的屈曲临界载荷Na随径向边界刚度kz的变化曲线。图4(d)所示为在非冲击端设置其他3个方向边界刚度无穷大，仅改变径向旋转边界刚度Kz时，受轴向冲击圆柱壳的屈曲临界载荷Na随径向旋转边界刚度Kz的变化曲线。从图4可以看出，边界刚度与厚径比一定时，圆柱壳的屈曲临界载荷Na随着轴向波数m增大而增大，说明轴向波数越高，圆柱壳越难屈曲。

分析各种边界条件下，圆柱壳厚径比(h/R)的改变对屈曲临界载荷Na的影响，可以看出边界刚度一定时，随着厚径比增大，屈曲临界载荷值增大。说明一般边界条件下，厚径比越大，圆柱壳越难屈曲。

可以将图4的曲线分成敏感区域和非敏感区域，在敏感区域圆柱壳屈曲临界载荷随刚度系数增大而急剧降低，在非敏感区域临界载荷随刚度系数增大而缓慢降低，直至不变。可以看出轴向、周向、径向和径向旋转各个方向刚度较小时为敏感区域，较大时为非敏感区域。说明各个方向的边界刚度系数越小，圆柱壳越难屈曲。且圆柱壳的屈曲临界载荷关于4个方向的边界刚度的敏感区域不同。

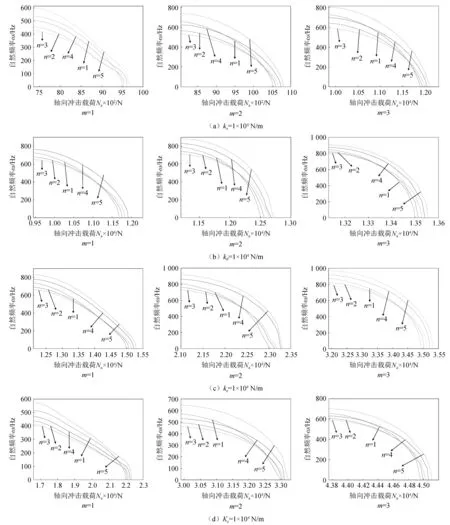
图3 圆柱壳自然频率随轴向冲击载荷的变化 Fig.3 The natural frequency versus the axial impact load

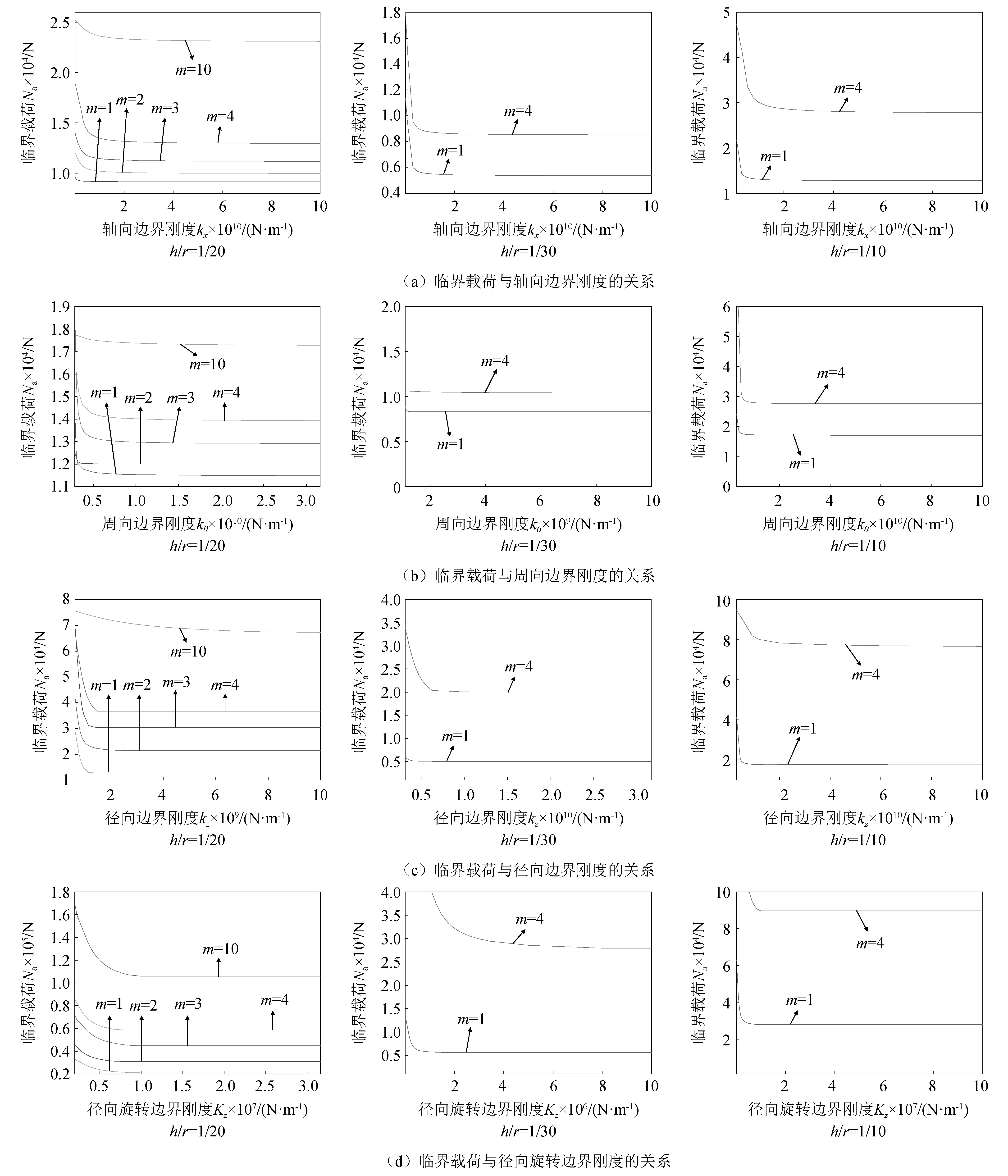
图4 屈曲临界载荷随边界刚度的变化Fig. 4 The critical load versus the boundary stiffness

4.3 不同边界条件下圆柱壳的周向屈曲模态

受轴向冲击的圆柱壳在两种不同边界条件下的周向屈曲模态可根据式(25)由式(6)得到，分别取n=1,2,3,4,5的5阶周向模态,其中m=1,h=0.002 m,R=0.04 m，ω=0。

图5所示为不同边界条件下受轴向冲击圆柱壳的周向屈曲模态。可以看出边界条件不同，圆柱壳周向屈曲模态也不同，即圆柱壳受轴向冲击时，边界条件的改变会影响周向屈曲模态形状。

图5 受轴向冲击的圆柱壳周向屈曲模态Fig.5 Circumferential buckling modes of the cylindrical shell

5 结 论

本文研究了4个方向弹簧约束下受轴向冲击圆柱壳的动力屈曲，并且对其自然频率进行了讨论。经计算分析得到如下结论：

(1)讨论了一般边界条件对受轴向冲击圆柱壳自然频率的影响，一般边界条件下，随着轴向波数的增加圆柱壳自然频率增大。且在敏感区域，自然频率随各个方向边界刚度增大快速增大，在非敏感区域，自然频率随边界刚度增大缓慢增大，直至稳定不变。圆柱壳的自然频率关于4个方向边界刚度的敏感区域不同。

(2)讨论了一般边界条件对圆柱壳屈曲临界载荷的影响，一般边界条件下，圆柱壳厚径比越大越难屈曲。且随着轴向波数的增加圆柱壳的屈曲临界载荷增大。在敏感区域，屈曲临界载荷随各个方向边界刚度增大而急剧降低，在非敏感区域，临界载荷随边界刚度增大而缓慢降低，直至不变。圆柱壳的临界载荷关于4个方向边界刚度的敏感区域不同。

(3)讨论了轴向冲击载荷对一般边界条件下圆柱壳自然频率的影响，一般边界条件下，圆柱壳的自然频率随着轴向冲击载荷增大而降低，且周向边界刚度和径向边界刚度的改变对自然频率影响比较明显。随着周向波数增大，圆柱壳的屈曲临界载荷也增大。

(4)讨论了一般边界条件下受轴向冲击圆柱壳的周向屈曲模态，圆柱壳受轴向冲击时，边界条件的改变会影响周向屈曲模态形状。

附录A

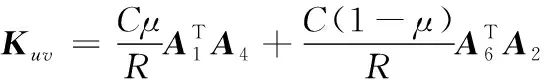
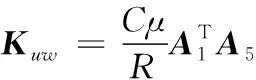
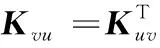
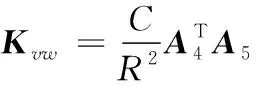
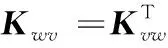
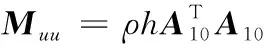
附录B