刚性耦合三圆柱流致振动特性和机制
2022-06-29刘旭菲陈威霖及春宁
刘旭菲, 陈威霖, 及春宁
(1. 浙江水利水电学院 水利与环境工程学院,杭州 310018;2. 天津大学 水利工程仿真与安全国家重点实验室,天津 300072)
多圆柱流致振动常见于海洋工程、桥梁以及核工程等,如海洋立管、桥梁缆索和热交换管等,对该问题的研究具有重要的科学和工程意义。作为经典的流固耦合问题,圆柱流致振动问题在过去的几十年中得到了广泛的关注。Sarpkaya等[1-2]对单圆柱涡激振动的研究成果进行了详细的综述。由于复杂的相互作用,多圆柱流致振动的振动特性和诱发机制十分复杂,明显不同于单圆柱的情况。Brika等[3-4]发现在串列布置中,在上游圆柱尾流的影响下,下游圆柱的振动受到显著的促进作用,出现了弛振的现象。陈威霖等[5-6]详细讨论了小间距比下串列双圆柱涡激振动中的振动响应、流体力及尾流模式等。Huera-Huarte等[7-8]发现当间距比不大时,并列双圆柱之间存在强烈的相互作用。Chen等[9]发现在并列布置下,对称布置的双圆柱会出现不对称振动现象。Behara等[10-11]发现在三角排列三圆柱中,下游两圆柱在上游圆柱尾流的作用下出现了较大振幅的振动,且出现了显著的多频现象。Chen等[12-13]发现在三角形布置下,随着间距比(P/D,P为圆柱中心之间的距离,D为圆柱的直径)的变化,振动响应可以划分为5个不同的区域,每个区域内圆柱的振动情况与P/D有密切关系。Ma等[14-15]通过拖曳水池试验研究了三角排列细长柔性圆柱的振动模态随折合流速变化的情况,对三圆柱之间的尾流/临近干涉和顺流向与横流向振动之间的相互作用进行了细致地分析。
除了上述单圆柱和独立支撑多圆柱流致振动问题,刚性耦合地多圆柱振动也常见于实际工程,如海洋工程中采用刚性管卡连接的立管束以及核工程中热交换管等。与独立支撑多圆体相比,在刚性耦合下多圆柱振动同步,其振动特性和振动机理与独立支撑多圆柱明显不同。由于各圆柱在耦合系统中的位置不同,它们对系统振动的贡献是重要的研究方向。本文侧重于揭示刚性耦合三圆柱的振动机制以及各圆柱对振动系统流体力的贡献,有助于促进对刚性耦合系统的理解。在刚性耦合多柱体的研究上,Munir等[16]对刚性耦合并列双圆柱的流致振动进行了数值模拟。雷诺数为Re=1 000,质量比为m*=2,间距比为P/D=1.5~4.0,折合流速为Ur=1~20。研究发现,当P/D=1.5~2.0时,系统振动分为两个分支,锁定分支内振动和升力同频,而非锁定分支内,振动频率为升力频率的一半。当P/D=4.0 时,尾流之间的相互作用变弱,振动锁定区域与单圆柱涡激振动相当。Han等[17]研究了不同来流攻角下等边三角形排列刚性耦合三圆柱的流致振动。其中,间距比固定为P/D=4.0,来流攻角α=0°~60°,折合流速Ur=1~30,雷诺数Re=1 000~3 000。研究发现,来流攻角和折合流速对涡激振动和脱涡模式都有显著的影响。当α=45°时,振动系统锁定范围最广,而当α=60°时,锁定范围最窄,在α=0°工况下出现弛振现象(Ur>12)。
尽管前人对刚性耦合多圆柱体的流致振动开展了一些研究,但由于此类问题的影响因素众多,已有研究仅能窥见一斑。基于此,本文针对实际工程中出现的等边三角形排列刚性耦合三圆柱系统的流致振动进行数值模拟研究,以期对其振动、受力特性和激励机制进行分析和探讨。
1 数值方法
1.1 控制方程
黏性不可压缩流动的控制方程[18]如下
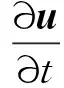
(1)
∇·u=0
(2)
式中:u为流速;t为时间;p为压强;ρ为流体密度;ν为运动黏滞系数; ∇为梯度算子;f为附加体积力矢量,代表流固耦合边界条件。
时间离散后的控制方程守恒形式如下
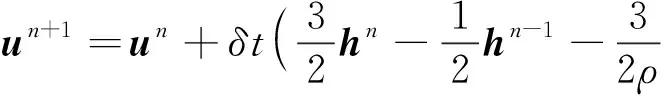
(3)
∇·un+1=0
(4)
式中:δt为时间步长; 组合项h=∇·[-uu+ν(∇u+∇uT)]由对流项与扩散项组成, 上标T为矩阵转置,附加体积力表示为
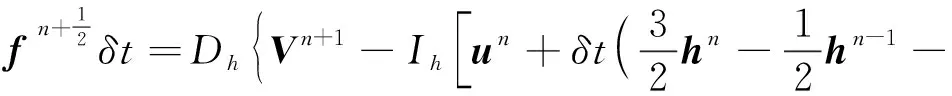
(5)
式中:Ih和Dh为引入的插值函数;Vn+1为物面边界点速度; 上标n+1,n+1/2,n,n-1为时间步。
仅做横流向运动的刚性耦合圆柱体,其运动可以用式(6)来描述
(6)
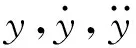
1.2 参数设置
刚性耦合三圆柱流致振动的模拟中,计算域流向X和横向Y的宽度分别为Lx和H。Lx=Lu+Ld,三圆柱圆心间距为P,圆心的中点距上游边界Lu=100D,距下游边界Ld=100D,H=200D,D为圆柱的直径,如图1所示。此外,为保证模拟结果的准确性,在圆柱周围设置一个大小为8D×8D的加密区域,区域内流向和横向网格大小均为1/64D。加密区域外的网格等比增大。计算域边界条件设置如下:入口为Dirichlet型边界条件;流向速度u=U∞;横向速度v=0;其中,U∞为无穷远处的流速。出口为Neumann边界条件,上下边界为自由可滑移边界。本文计算域和网格的设置与Chen等的研究相同,其参数敏感性已经在Chen等的研究中证明。
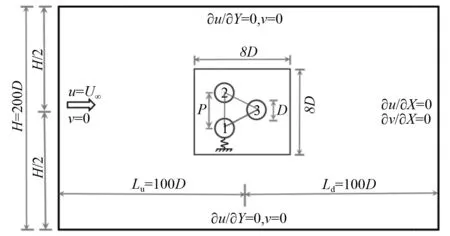
图1 正三角形排列刚性耦合三圆柱流致振动的计算域和边界条件示意图Fig.1 Sketch of computational domain and boundary conditions for flow-induced vibration of three rigidly coupled cylinders in equilateral-triangular arrangements
刚性耦合三圆柱按等边三角形布置,上游为两个并排圆柱,下游为一个圆柱,三圆柱的间距比为P/D=1.0~4.0,质量比为m*=2,雷诺数为Re=100和折合流速为Ur=3~30。为了保证圆柱能以更大振幅振动,阻尼比设为零。耦合三圆柱仅在横向自由振动。
需要说明的是,本文数值方法的模拟精度已经在独立支撑的三圆柱涡激振动研究中得到了充分验证,读者可自行查阅,此处不再赘述。
2 结果与讨论
2.1 振幅与响应频率
不同间距比下刚性耦合三圆柱的无量纲振幅A/D和频率比f*随折合流速变化情况,如图2所示。由图2(a)可知:不同间距比下,刚性耦合三圆柱的振动呈现出明显不同的变化趋势。当P/D=1.0时,振动响应表现为典型的弛振响应[19-20],振幅随折合流速的增加而单调增加,而振动频率比f*(f*=fv/fn,fv为振动频率,fn为系统固有频率)则一直小于1.0。当P/D=1.0时,位移历时曲线的情况,如图3(a)~图3(e)所示。图3中横轴为无量纲时间t*=tU∞/D,纵轴为无量纲位移y/D。总体上看,圆柱的位移呈现正弦变化,比较规律,这与相似雷诺数下三角柱的驰振响应类似。当Ur=25时,圆柱的振动出现微弱的拍振特征。所谓拍振是指振动响应中包含两个或以上振动分量,并且各个分量的频率非倍数关系,造成了振幅的大小随时间周期性变化。
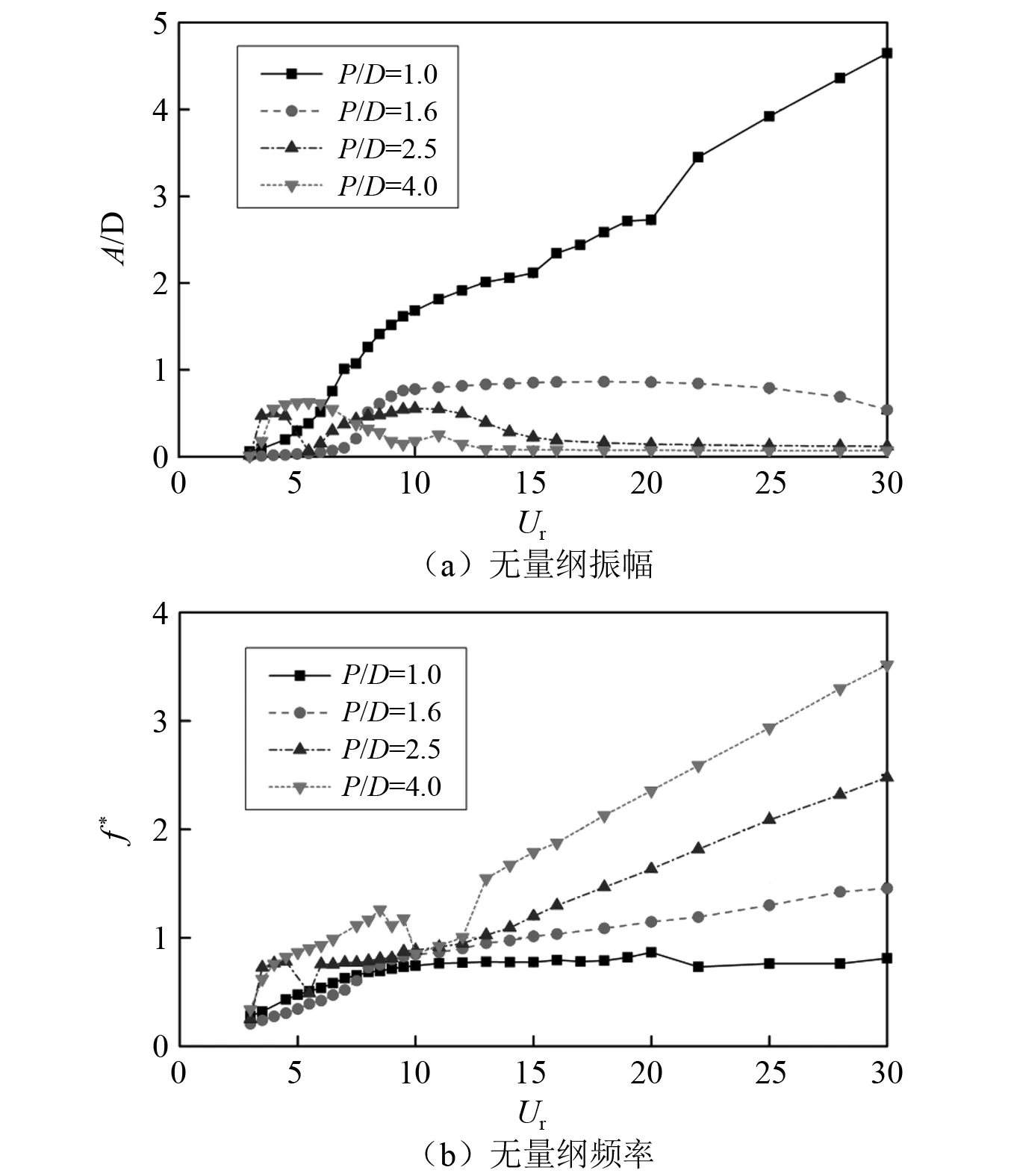
图2 不同间距比下正三角形排列刚性耦合三圆柱振幅和频率随折合流速的变化Fig.2 Variations of the vibration amplitude and frequency of three rigidly coupled cylinders in equilateral-triangular arrangements with the reduced velocity under different spacing ratios
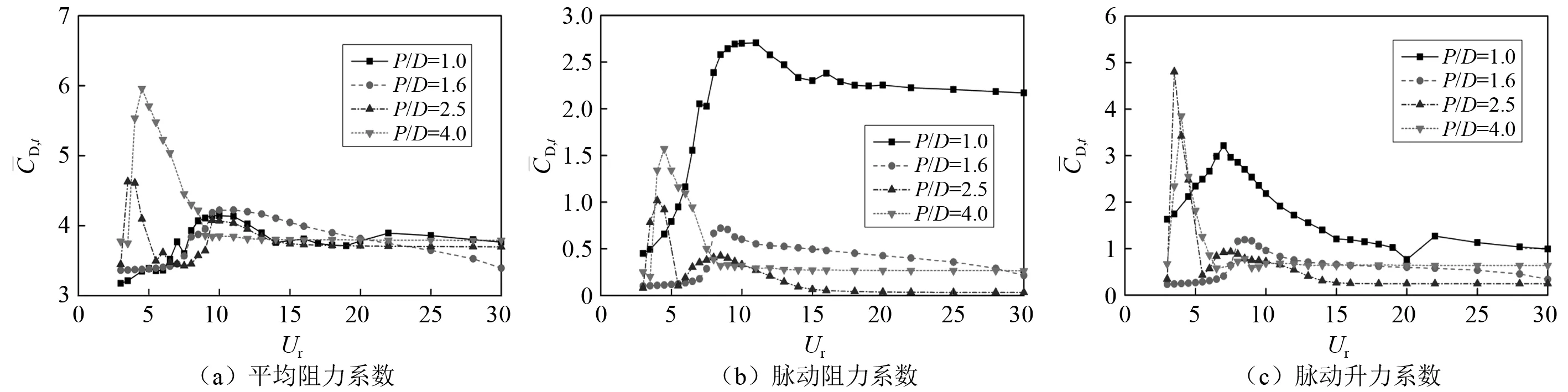
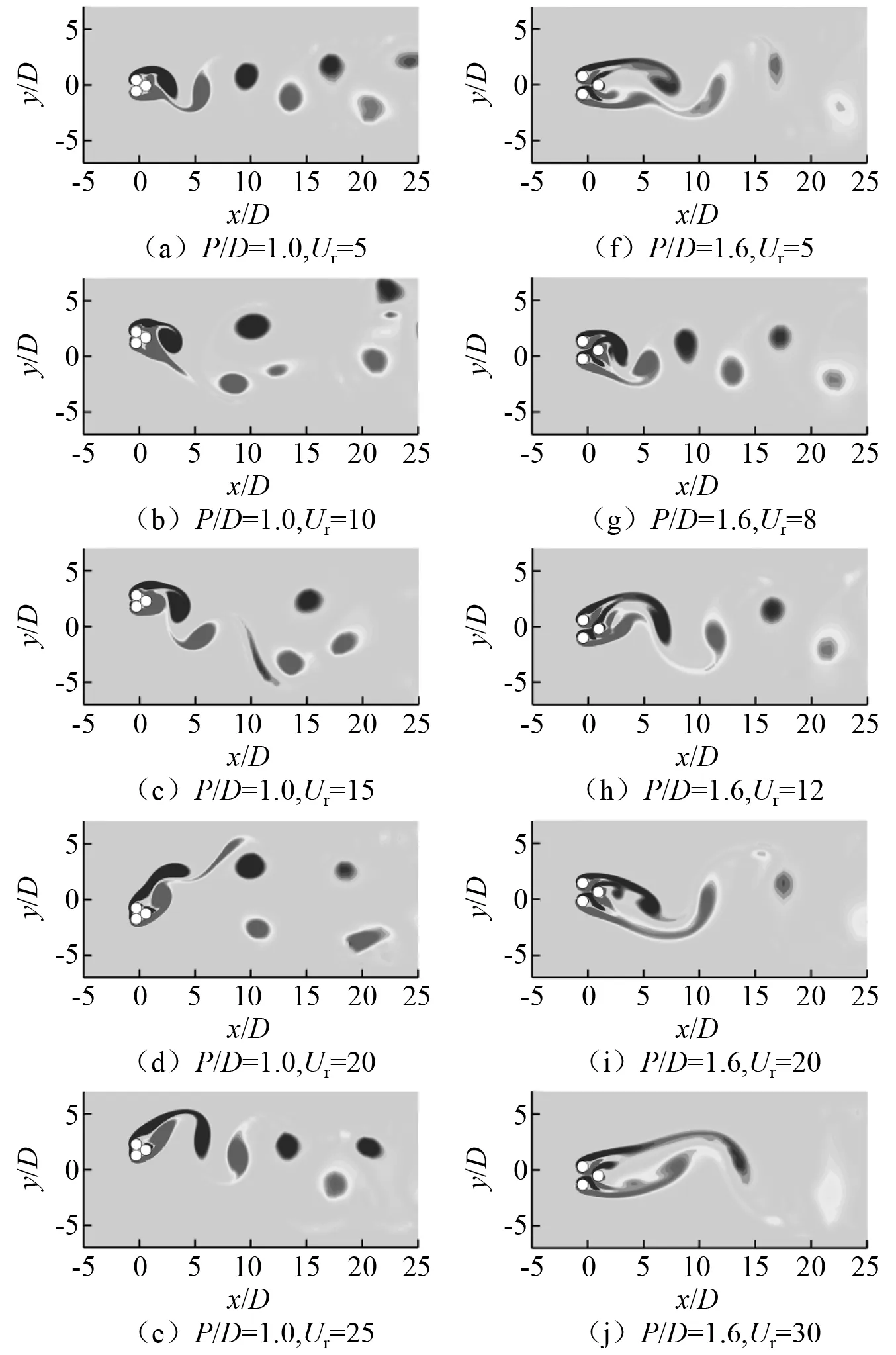
当P/D=1.6时,振幅明显小于P/D=1.0时的工况。由图2(a)可知:当Ur≤7.5时,振幅几乎为零。之后,随着折合流速的增加,振幅持续增加,并在很宽的折合流速区间内维持稳定的振幅,最大振幅为A/D=0.86。当Ur>22以后,振幅开始缓慢下降。由图2(b)可知:当Ur≤7.5时,振动频率随折合流速线性增加,对应静止工况下的泄涡频率斯特劳哈尔数St。当Ur>7.5时,振动频率偏离St,而沿着一个更小的斜率近似线性增加。在锁定区间7.5 当P/D=2.5时,以Ur=5.5为界,振动可以分为两个锁定区间。两个区间内圆柱的振动均呈现为先增后减的趋势,最大振幅相当,但是后一个区间的宽度明显大于前一个。由图2(a)可知:在第一个区间(Ur=3.5~4.5)内,圆柱振动响应随折合流速变化较为剧烈,上升段和下降段均较陡,最大振幅(A/D=0.50)出现在Ur=4处。由图2(b)可知:在第二个区间(Ur=6~15)内,振幅的上升段和下降段均较缓,最大振幅(A/D=0.55)在Ur=10处取得。与P/D=1.0,P/D=1.6工况相比,振幅明显更小一些。振动频率在两个区间内也呈现不同的变化趋势。在第一个区间内,振动频率维持在f*=0.8附近,振动处于锁定状态。在第二个区间内,振动频率维持在f*=0.8~1.2内,振幅也较大一些。在两个锁定区间之间(Ur=5.5)和之外(Ur=3和Ur>15),振幅较小,振动频率与静止工况下的St接近,随着折合流速线性增加,振动处于非锁定状态。当P/D=2.5时圆柱位移的历时曲线,如图3(k)~图3(o)所示。在两个锁定区间内部,圆柱的振动均较为规律,而在区间交界处,振动响应呈现拍振特征。总的来看,当P/D=2.5时,刚性耦合三圆柱的振动响应呈现出双锁定区间的特征,这与单圆柱的单锁定区间形成了鲜明的对比。此外,两锁定区间的尾涡与圆柱之间的相互作用有明显差异,产生了截然不同的激励作用。 当P/D=4.0时,振幅随折合流速的变化情况与P/D=2.5工况的类似,可划分为振幅较大的第一锁定区间(Ur=4.0~8.5)和振幅较小的第二锁定区间(Ur=10~12)。由图2(a)可知:在第一区间内,随着折合流速的增加,振幅迅速增加,并在Ur=5.5时达到最大值(A/D=0.63)。之后,随着折合流速的增加,振幅缓慢下降,直到第一个区间结束;在第二区间内,振幅的变化明显小于第一区间的情况,最大振幅仅为A/D=0.25。由图2(b)可知:虽然第一区间的振幅明显大于第二区间,两个区间的振动频率均在f*=0.8~1.2内。两个区间之间,振动频率出现了明显的跳跃和不连续现象。当P/D=4.0时,圆柱位移的历时曲线,如图3(p)~图3(t)所示。在第一个锁定区间内,振动响应均为规律的正弦曲线;而在第二个锁定区间内,振动响应表现为规律的非对称振动,呈现出明显的多频特征,这与圆柱尾流之间复杂的相互作用有关。 图3 不同折合流速下正三角形排列刚性耦合三圆柱的位移历时曲线Fig.3 Displacement histories of three rigidly coupled cylinders in equilateral-triangular arrangements at different reduced velocities 综合以上的结果可知,不同间距比下三角形排列刚性耦合三圆柱流致振动响应可大致分为两类:一类是间距比较小情况下的驰振响应(不稳定性激励),圆柱振动幅值随折合流速近似线性增大,振动频率小于体系的固有频率,这与直边迎流的三角柱的振动响应类似,换句话说,由于圆柱之间的间隙流较弱,3个刚性耦合的圆柱可近似视为一个扩展了的三角柱;另一类为间距比适中和较大情况下的涡激振动响应(共振激励),但不同间距比下会产生单锁定区间和双锁定区间的振动响应。由于圆柱之间距离较小,P/D=1.6工况下仅有一个锁定区间,而且对比锁定区间内的频率特征可以发现,P/D=1.6工况的单锁定区间是与P/D=2.5,P/D=4.0双锁定的第一锁定区间相对应。 图4 不同间距比下三角形排列刚性耦合三圆柱的流体力系数随折合流速的变化Fig.4 Variations of the hydrodynamic force coefficients of three rigidly coupled cylinders in equilateral-triangular arrangements with the reduced velocity under different spacing ratios 不同间距比下脉动阻力C′D,t随折合流速变化的情况,见图4(b)。P/D=1.0工况的脉动阻力明显大于其余间距比的情况。与阻力均值相似,脉动阻力在Ur>14以后几乎不再变化,维持在C′D,t=2.2附近。当P/D=1.6时,脉动阻力随折合流速的增加先增加后减小,呈现单峰特征。当P/D=2.5,P/D=4.0时,脉动阻力随折合流速的变化趋势与阻力均值相似,分别呈现双峰和单峰特征。 不同间距比下脉动升力C′L,t随折合流速变化的情况,见图4(c)。从总体上看,除个别折合流速,P/D=1.0工况的脉动升力要比其余工况的更大一些,随着折合流速的增加,脉动升力先增后减,最大值(C′L,t=3.21)出现在Ur=7处。而当P/D=1.6时,脉动升力在Ur=8.5时达到最大值(C′L,t=1.19),之后开始缓慢下降。当P/D=2.5,P/D=4.0时,脉动升力均表现出双峰特征,尽管P/D=4.0工况的第二个峰值(位于Ur=11处)很小且平缓。 为深入分析各间距比下圆柱振动与流场之间的耦合作用,本节结合尾流模式给出详细的机理解释。当P/D=1.0时,三圆柱紧密靠在一起,圆柱之间不存在间隙流,如图5所示。图5中,x/D和y/D分别为无量纲的流向和横向坐标。剪切层在刚性耦合三圆柱的上、下两侧形成旋涡,并交替泄放。由图5(a)可知: 当Ur=5时,旋涡从圆柱的两侧脱落,形成典型的2S泄涡模式。随着圆柱振幅的增加,单个振动周期内脱落的旋涡个数明显增多,形成了多涡模式,见图5(c)~图5(e)。需要说明的是,由于泄涡长度较长,图5(c)~图5(e)所示范围未能显示一个完整振动周期内的旋涡泄放。例如,图5(e)所示仅为半个振动周期内的旋涡泄放过程。驰振频率与泄涡频率相差很大,因此驰振不是由交替泄涡激发的,而是由三圆柱运动时上、下表面的时均压差引起和维持的。 当P/D=1.6时,圆柱间隙间形成剪切层。由于受到下游圆柱的束缚,上游圆柱的间隙剪切层仅发生小幅摆动,并不能脱落旋涡。上游圆柱的外侧剪切层可脱落旋涡,并与下游圆柱的剪切层融合,形成扩展的2S泄涡模式。对比P/D=1.0的工况可以发现,间隙流的出现使得P/D=1.6工况下旋涡更弱,且距离圆柱更远。此工况下,振动频率和升力频率相等,圆柱的振动由交替泄涡(扩展2S模式)驱动。 当P/D=2.5时,间隙流的作用更加显著,上游圆柱柱间剪切层大幅摆动,与下游圆柱发生复杂相互作用,一些情况下能脱落旋涡。不同间隙比条件下,柱间剪切层和下游圆柱的相互作用存在两种截然不同的模式。当Ur=4时(第一锁定区间),上游圆柱间隙剪切层交替脱落旋涡,并“抨击”在下游圆柱上,随后发生分裂,形成两个较小的旋涡,如图6(a)所示。此时,圆柱受到的脉动升力和阻力均较大(见图4(b)~图4(c)),振幅较大。上、下游圆柱的泄涡发生复杂的融合后,在下游形成较宽的平行涡街。但是,当折合流速更大时(Ur=6,Ur=10,Ur=12,Ur=20,第二锁定区间,如图6(b)~图6(e)所示),上游圆柱的剪切层不与下游圆柱发生直接作用,而是与下游圆柱的剪切层发生融合,形成扩展的交替涡街。可见,P/D=2.5工况下存在两种振动激励模式:一种是低折合流速条件下的剪切层重附着激励模式;另一种是中、高折合流速条件下的交替泄涡(扩展2S模式)激励模式。 图5 不同折合流速下正三角形排列刚性耦合三圆柱的尾涡模式(P/D=1.0,P/D=1.6)Fig.5 Wake patterns of three rigidly coupled cylinders in equilateral-triangular arrangements at different reduced velocities (P/D=1.0, P/D=1.6) 当P/D=4.0时,旋涡可以自由地从3个圆柱上脱落。当Ur=5时(第一锁定区间),从上游圆柱内侧脱落的旋涡交替地重附着于下游圆柱上,如图6(f)所示。此时,圆柱的脉动升力较大,振动由剪切层重附着驱动。旋涡经过复杂的融合后,在下游形成较宽的平行涡街。当Ur=8时,泄涡不规律,如图6(g)所示。当Ur=11时(第二锁定区间),上下游圆柱各自交替脱落旋涡,但上游圆柱的泄涡近似同相位,如图6(h)所示。从上游圆柱脱落的旋涡不直接与下游圆柱作用,而是与下游圆柱的旋涡共存,形成杂乱无章的尾涡模式。此时,振动由单个圆柱的交替泄涡驱动。进一步增大折合流速(Ur=15,Ur=25),两个上游圆柱的泄涡近似反相位(如图6(i)~图6(j)所示),上游圆柱的升力相互抵消,圆柱振幅很小。 图6 不同折合流速下正三角形排列刚性耦合三圆柱的尾涡模式(P/D=2.5,P/D=4.0)Fig.6 Wake patterns of three rigidly coupled cylinders in equilateral-triangular arrangements at different reduced velocities (P/D=2.5, P/D=4.0) 本文对等边三角形排列刚性耦合三圆柱的涡激振动问题进行了数值模拟研究,其中上游为两个并排的圆柱,而下游为一个圆柱。对不同间距比下振幅、频率和各圆柱的流体力贡献进行了详细讨论,最后结合尾涡模式,对圆柱与流场之间的相互作用进行了分析。 研究发现三角形排列刚性耦合三圆柱的振动模式分可以为两类,分别为P/D=1.0的驰振模式和P/D=1.6~4.0的涡振模式。当P/D=1.0时,无间隙流动,三圆柱形成一个扩展的整体,系统振动表现为直边迎流的三角柱相似的弛振特征。当系统振动较小时,从三圆柱表面交替脱落的旋涡形成2S模式,随着振幅的增加,单个振动周期内会脱落更多的旋涡。当P/D=1.6时,间隙流较弱,间隙内剪切层小幅摆动,但不会形成旋涡,三圆柱后方形成2S模式尾涡,并驱动三圆柱发生涡激振动。振动仅出现单个较宽的锁定区间。当P/D=2.5,P/D=4.0时,圆柱的振动呈现为两个锁定区间,分别对应不同的振动激励机制。第一个锁定区间内,上游圆柱的间隙剪切层脱落旋涡,并撞击到下游圆柱上,引起下游圆柱较大的脉动升力,从而激发圆柱振动,即剪切层重附着激励模式;第二个锁定区间内,上游圆柱的剪切层不与下游圆柱发生直接作用,而是与下游圆柱的剪切层发生融合,形成交替涡街,激发圆柱振动,即交替泄涡驱动模式。 需要说明的是由于本文仅研究了层流条件下刚性耦合三圆柱的振动特性和机理,然而在实际工程中流动为紊流,雷诺数多在105~107量级,因此,研究成果推广到实际工程具有一定的局限性。然而,尽管高雷诺数条件下刚性耦合三圆柱系统具有更大振幅,各圆柱尾流之间的相互作用更加强烈,但是一些现象以及机理是相通的。例如,本文的研究发现在间距比不大时,刚性耦合三圆柱表现为弛振现象,而在Han等的高雷诺数类似工况下同样也出现了弛振现象,其机理也与本文提到的剪切层的重附着有关。综上,本文研究成果对于深入理解实际工程的高雷诺数刚性耦合三圆柱涡激振动的现象和机制有一定帮助。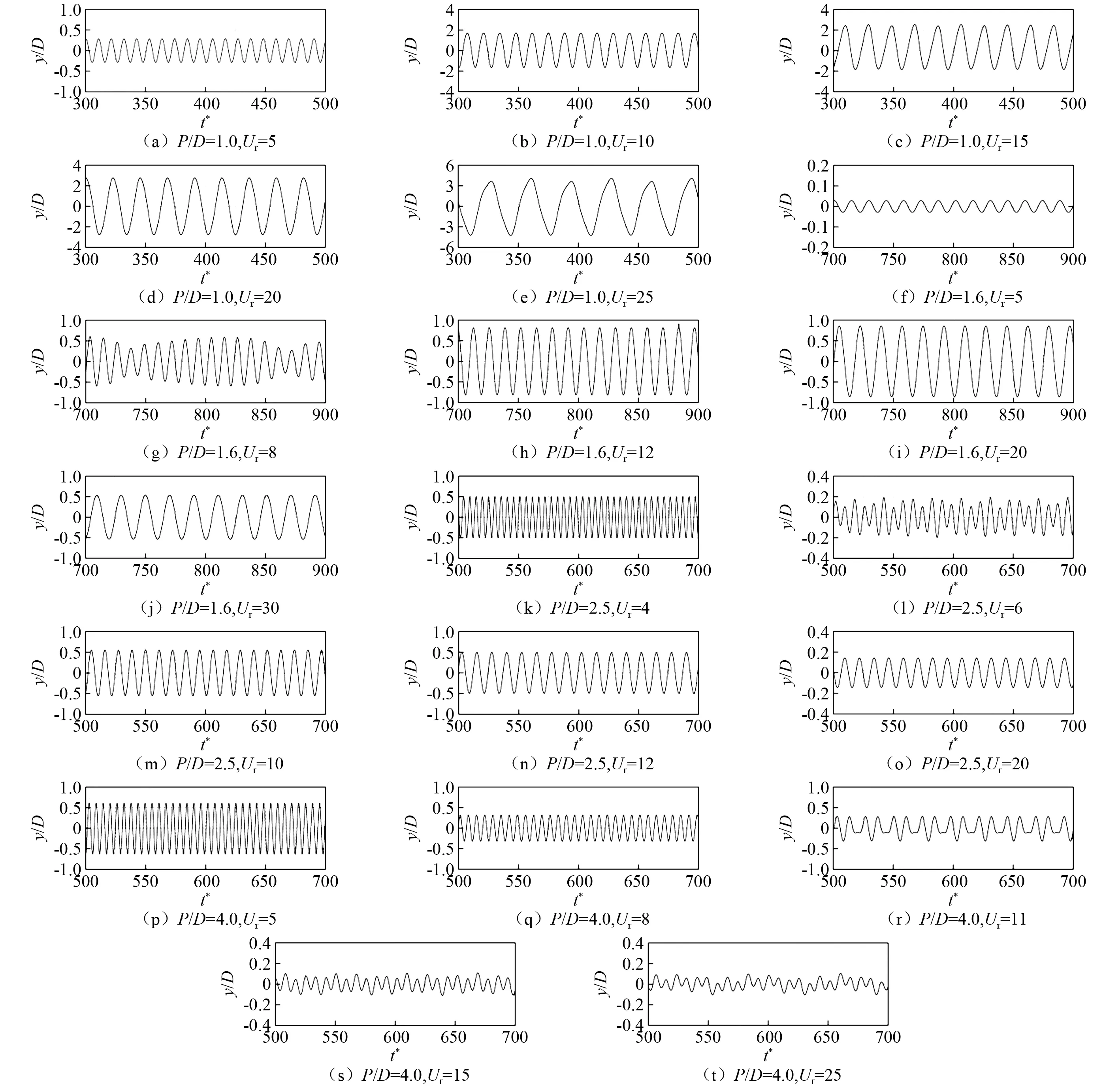
2.2 流体力系数
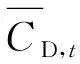
2.3 尾流模式和激励机制

3 结 论
