开关磁阻电机转矩脉动抑制研究*

徐 萌，王华宇，高 洁

(中国民航大学电子信息与自动化学院，天津 300300)

0 引言

开关磁阻电机(switched reluctance motor,SRM)具有结构简单、成本低、可靠性高、调速范围宽等优点，SRM在各个领域中都有很大的应用潜力[1-3]。在SRM控制系统设计时，高效、合理、贴近实际工况的控制系统仿真模型，便于改变系统各部分的结构和参数，可以充分利用计算机仿真的优越性，有效地节省设计时间和成本。

由于SRM固有的双凸极结构和非线性电磁特性，很大程度上限制了它在工业上的应用。如何能够更有效地抑制SRM换相过程中的转矩脉动，已经成为有关SRM的重要研究方向[4-6]。DAVARPANAH等[7]介绍了一种应用C型铁芯的12/14三相SRM，通过与常规的12/8三相SRM比较，说明该结构提高了SRM的平均转矩和转矩密度。CHOI 等[8]通过改变定转子的结构参数来影响气隙，再通过气隙影响电机的互感，从而减小转矩脉动。以上文献从SRM的本体结构方面做了优化，但优化过程繁琐单一，需要反复进行仿真实验。

ZHANG等[9]提出了将模糊逻辑引入转矩分配函数(torque share function,TSF)中，然后利用粒子群算法对模糊隶属函数进行优化，仿真结果表明该方法将转矩脉动减小了30%左右；RAMAIAH 等[10]提出了基于电机模型计算的TSF改进方法，利用有限元法分析电机的静态特性，进而重新确定TSF的理想形状，实验结果显示，该方法具有更好的电流和转矩跟踪性能，但是以上方法电机模型中的数据只是某一特定条件下得到的数据，如果要模拟SRM其他状态下的仿真情况，需要重新在Maxwell中进行分析。

针对以上问题，本文首先从电机本体入手，以更小的转矩脉动和更大的平均转矩为目标，利用遗传算法，对SRM定子和转子的极弧系数、外径等参数做优化，然后从SRM控制系统的控制策略入手，将SRM的总期望转矩分配到各相，将当前相期望转矩与实际转矩的差值和其导数的差值，补偿给下一相的期望转矩，形成可根据系统运行情况在线补偿的TSF，进一步减小SRM的转矩脉动，最后搭建基于 Maxwell-Simplorer-Simulink的联合仿真平台，该平台可以同时调整电机的结构参数和控制算法，改善SRM控制系统的运行情况，通过该平台验证本文所提内容对于SRM转矩脉动的优化效果。

1 SRM转矩脉动抑制

1.1 SRM本体结构参数优化

开关磁阻电机的转矩近似线性模型[13]可表示为：

(1)

式中，T(k)为第k相绕组的瞬时转矩；∂Wc(θ,i(k))为磁共能；L(k)为相电感。由式(1)可知，SRM的电磁转矩大小与相电流、绕组电感和位置角有关。电感与磁导率等物理量有关，所以定、转子的极弧系数、内径、外径和两者之间的气隙等结构参数都会影响电感的大小，从而影响SRM的转矩[3]。本文选取定、转子极弧系数和定、转子外径这两组对SRM转矩特性影响较大结构参数来分析。

首先，分析定、转子极弧系数对SRM转矩特性的影响。利用Maxwell计算不同定、转子极弧系数对SRM的平均转矩和转矩脉动的影响，以0.04为步长改变定子和转子极弧系数，如图1和图2所示，SRM平均转矩的幅值随着定、转子极弧系数减小呈增大的趋势，但是随着定子极弧系数减小又会引起转矩脉动增大，所以不能一味追求小极弧系数。

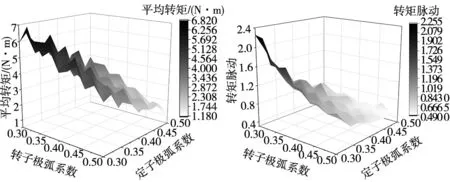
图1 不同定、转子极弧系数的平均转矩 图2 不同定、转子极弧系数的转矩脉动

然后，分析定、转子外径对SRM转矩特性的影响。令定子轭厚不变，改变第二气隙，以1 mm为步长改变定、转子外径，SRM的平均转矩和转矩脉动随定、转子外径变化的情况如图3和图4所示。可以看出定、转子外径对于平均转矩和转矩脉动的影响是强非线性的。

图3 不同定、转子外径的平均转矩 图4 不同定、转子外径的转矩脉动

以上分析可以得到，SRM的优化设计是一个多目标、多参数耦合的非线性优化问题[5]，本质是为了改善电机的综合性能，电机的各结构参数相互妥协的过程[13]，本文选取定、转子极弧系数和定、转子外径为优化变量。

遗传算法是一种典型的全局寻优智能算法，十分适合用于SRM的结构优化。本文以减小SRM转矩脉动和增大平均转矩为目标，将多目标优化问题，利用加权求和转化为单目标优化求解问题[14]，然后利用遗传算法求解。

MOXA非常积极的拥抱各种前沿技术，在引领技术趋势同时，希望让客户可以享受到技术带给大家的便利性。MOXA始终坚持为天下工业人打造一个稳定、可靠和安全的通信系统，真的做到了以现场场景出发，为用户着想，让客户用着放心。

SRM的转矩脉动表示为：

(2)

式中，Tmax为最大转矩；Tmin为最小转矩。

该多目标优化问题表示为：

(3)

式中，Tav为平均转矩；ω1、ω2为权重系数，ω2为负数且|ω1|+|ω2|=1；m为SRM相数；Nr为SRM转子齿数；βs为定子极弧；βr为转子极弧。

1.2 SRM在线补偿转矩分配函数设计

在SRM相绕组换相期间，按照常规控制方法开通、关断相电流会导致开通相形成的转矩增加量将不足以抵偿关断相引起的转矩减小量，合成转矩在这一过程明显跌落。针对该问题，TSF将电机的总转矩分配给各相，在相邻相换相期间建立重叠区间，在该区间内由开通相和关断相共同产生转矩，本文选取余弦型TSF。

(4)

式中，θon为导通角；θoff为关断角；θov为重叠角；τr为周期；Tref(k)为第k相参考转矩；Tref为总参考转矩。

由式(1)可知SRM的实际转矩与电流的平方和相电感的变化率成正比。在SRM换相的开始阶段，定转子一般处于不对齐位置，在SRM换相的结束阶段，定转子处于接近对齐的位置。由于SRM特有的凸极结构，当定子和转子在不同的相对位置时，相电感和相电感的变化率均不同，在换相过程中，会导致电机的实际转矩难以跟踪上给定转矩[15]。所以虽然TSF从理论上能很好的弥补换相过程的转矩降落，但是由于SRM电感变化的非线性，仍然会产生转矩脉动的问题。

本文将在线补偿机制引入TSF，使总的参考转矩通过改进后的TSF实现更合理的转矩分配，其算法示意图如图5所示。

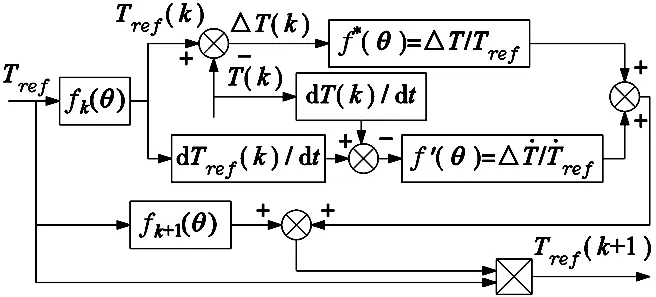
图5 SRM转矩分配补偿策略示意图

首先计算出当前相绕组产生的转矩和给定转矩的差值与转矩变化率的差值，表达式为：

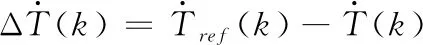
(5)

(6)

(7)

(8)

转矩误差经过补偿，通过式(7)转化为对后一相TSF的修正补偿值Δf*，此时后一相补偿之后的TSF以及新的后一相参考转矩可以分别通过式(7)和式(8)得到。

本文设计的在线补偿TSF控制方案的特点在于让当前关断相的转矩按照给定的TSF曲线减小，然后根据当前相转矩的实时反馈，将当前相的期望转矩与实时转矩的差值和二者导数的差值补偿给下一相，使其补足关断相的误差。

2 联合仿真平台

本文中，Maxwell主要用于优化电机本体结构参数，Simplorer用于搭建电机的驱动电路，Simulink用于设计SRM控制系统的控制算法。三者的关系和在SRM控制系统中的作用如图6所示。

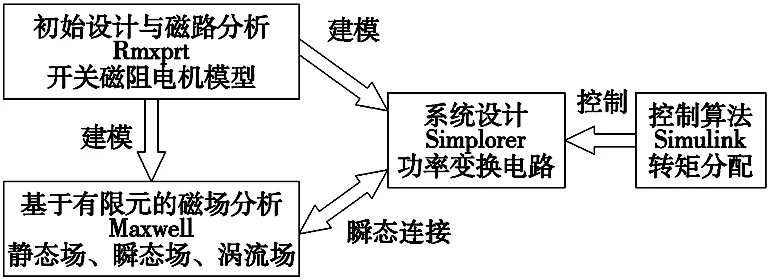
图6 Maxwell-Simplorer-Simulink仿真软件关系图

SRM控制系统由转速、转矩双闭环构成。系统框图如图7所示，外环是转速控制环，内环是转矩控制环。控制系统的转速信号经过速度控制器处理后，产生转速外环的输出信号，该输出信号再作为转矩内环的预期转矩，预期转矩经过转矩分配函数处理，通过功率变换器控制SRM运转。

图7 SRM控制系统框图

本文利用某公司的 RMxprt工具快速实现SRM的初始方案评估。在Maxwell中建立SRM有限元模型，其主要过程为：把SRM基本参数输入RMxprt中生成二维模型，然后导入Maxwell中，利用求解器对电机模型分析计算。在Maxwell中生成的有限元模型里定义SRM的各部分材料、绕组的激励源和边界条件等。最后确定运动界限、转子转速、网格剖分情况及有限元分析的时间步长等[16]。

图8为SRM驱动电路在Simplorer软件中的部分，主要包括8个晶闸管、8个续流二极管，SRM本体模型由Maxwell导入到Simplorrer环境中。对SRM的控制建立在对8个晶闸管控制的基础上，相应的触发逻辑由Simulink控制单元完成。Simulink控制单元输出8路脉冲信号到Simplorer控制单元，Simplorer与Maxwell软件进行数据交换获得SRM的电流、电压、转子角度、负载转矩、电磁转矩等参数后，将数据传入Simulink控制单元，Simulink控制单元根据这些数据信息和在线补偿TSF产生脉冲信号。

图8 Simplorer中的模型

3 仿真结果分析

本文中电机的初始结构参数如表1所示。

表1 电机初始结构参数

3.1 基于Maxwell的SRM结构性优化结果

图9为遗传算法代价函数的情况，图10为经过优化后的转矩情况。经过优化后的转矩脉动减小了14.20%。电机的结构参数与性能对比如表2所示。

图9 遗传算法代价函数图 图10 改进前后转矩对比图

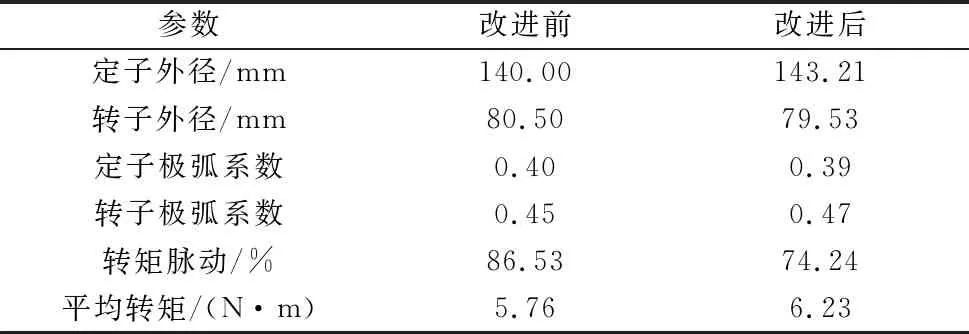
表2 电机参数优化对比表

3.2 基于联合仿真平台的实验结果

本文SRM采用直流310 V供电，给定转速为1000 r/min，负载转矩为8 N·m。

图11为常规TSF算法下的相电流、转矩波形，图12为在线补偿TSF算法下的相电流、转矩波形，两种控制器正常运行时的具体数据如表3所示。

(a) 常规TSF相电流 (b) 常规TSF转矩

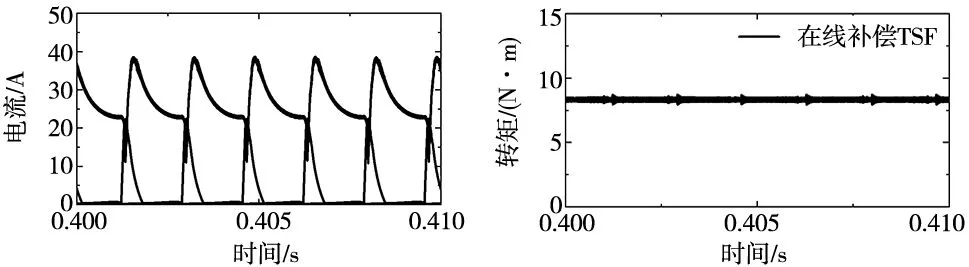
(a) 在线补偿TSF相电流 (b) 在线补偿TSF转矩

表3 正常运行3种控制器性能对比

由表3、对比图11与图12可以发现加入在线补偿机制后，转矩脉动从19.4%减小到4.5%，整体的转矩控制效果也更加优秀，同时减小了SRM控制系统的电流尖峰，这是由于关断时的相电感远远大于开通时的电感，关断时电流下降的速度会慢于正常情况下的电流上升速度，导致关断相的转矩下降慢于给定的TSF，引入补偿策略后，让导通相的TSF减去关断相形成的转矩差值，可以减小转矩脉动和电流尖峰。

4 结论

本文针对SRM控制系统在换相阶段转矩脉动的问题，首先从SRM本体入手，利用遗传算法，对SRM的结构参数进行优化；然后从SRM系统的控制策略入手，设计了在线补偿TSF控制策略；最后搭建了基于Maxwell-Simploer-Simulink的联合仿真平台，该平台能够实现同时从电机本体和控制策略两方面优化SRM控制系统的性能。

结果表明，本文改善了电机本体的转矩脉动，利用在线补偿TSF从整体上改善了系统的转矩脉动和电流尖峰问题，联合仿真平台也为以后改进电机的结构和验证其他控制算法提供了方便。