基于改进人工势场法的机械臂路径规划*
2022-06-29王宪伦王天宇丁文壮
王宪伦,王天宇,丁文壮
(青岛科技大学机电工程学院,青岛 266061)
0 引言
制造业智能化快速发展的背景下,以机器人为代表的智能设备在产品生产过程中自动化应用愈加广泛[1]。实现机器人自主作业,需要各类传感器的加持,更需要机器人能够进行快速可靠的路径规划。
目前,常用的路径规划方法主要有以下几种:A*算法[2]、快速扩展随机树(RRT)[3]、蚁群算法[4]及人工势场法[5]等。其中,人工势场法凭借其简单直接的数学描述的优点,在机器人路径规划领域应用广泛。该算法结构简单,实时性好,生成路径较为平滑,但是也存在一些问题,如易陷入局部最小值陷阱和目标不可达等[6]。陈劲峰等[7]提出一种逃离或穿越的策略以解决局部最小值问题。XI等[8]将人工势场法与RRT算法结合,利用偏目标的RRT方式引导跳出局部最小值,并提高规划效率。SANG等[9]将A*算法与人工势场法结合,将路径分为多目标点并实现切换,极大降低陷入最小值的可能。以上学者等针对人工势场法的缺点进行了改进,但是目前包括其在内的多数学者仍主要以移动机器人为研究对象,而算法随机器人维度的增加计算更为复杂,因此针对多自由度的三维机械臂领域进行研究仍是一重点方向。
本文以三维机械臂为研究对象,针对原算法不足之处进行改进,包括对不同距离下的引力斥力函数重新定义,给出一种跳出局部最小值陷阱的解决方案,并对求解路径进一步优化,最后在仿真平台验证了改进算法应用于机械臂的有效性。
1 碰撞检测及控制点设置
1.1 建立碰撞检测模型
现实场景中各类物体外形复杂,机械臂与障碍物进行有效的碰撞检测是路径规划的前提。目前机械臂的碰撞检测主要有传感式和建模式,其中建模式不需外部传感设备,在碰撞发生前即可预警,因此在实际应用中该方法更为常用[9]。
包围盒算法是建模式碰撞检测中的常用方法[10],算法基本思想是用体积稍大且特性简单的几何体来近似地代替复杂的几何对象。常见的包围盒算法有包围球、AABB包围盒、OBB包围盒等,各包覆效果如图1所示。

图1 包围盒包覆效果对比
其中,OBB包围盒[11]可以根据被包围对象的形状特点尽可能地包覆对象,同时可以涵盖被包围物体的姿态信息,与另外两种类型包围盒相比虽然计算复杂度有所增加,但本文研究所用机械臂和障碍物外形规整,权衡之下该法更优。
故本文采用DH参数法对机械臂运动学建模后,基于OBB包围盒算法以圆柱体包覆机械臂建立碰撞检测模型。具体建模规则为:以机械臂坐标系原点间距作为母线长度,以坐标原点所在平面作为圆柱体上下圆面,以机械臂各连杆半径作为圆柱体半径,搭建模型如图2所示。

图2 机械臂碰撞检测模型
机械臂与障碍物进行距离检测时,为简化模型,视机械臂连杆为线段,扩大障碍物体积补偿简化的包覆圆柱体直径,碰撞与否根据障碍物中心点与连杆线段关系的两种情况判断。
第一种情况:点在线段上。该情况发生时,机械臂已与障碍物碰撞。
第二种情况:点在线段外。在此用三点法进行判断。计算连杆线段的两端点P1、P2和中点Pm与障碍物中心点O距离,设点P1、P2和Pm与点O距离分别为d1、d2和dm。
若d1>dm>d2或d2>dm>d1,点O与线段垂线投影在线段延长线上,此时碰撞检测最小距离为d2或d1,如图3上面两幅图所示;若d1>dm 图3 碰撞检测最小距离确定方法 运用人工势场法进行路径规划需要将工作空间中的力映射到机械臂关节空间。根据虚功原理可得到机械臂工作空间与构型空间的力和力矩转换关系,如式(1)所示。 F·(δx,δy,δz)T=T·δq (1) 式中,F为工作空间广义力;(δx,δy,δz)为工作空间中虚位移;δq为构造空间中虚位移。 根据机械臂雅可比矩阵定义有: (δx,δy,δz)T=J·δq (2) 式中,J为机械臂雅可比矩阵。 式(1)和式(2)联立可得: T=JT·F (3) 通过式(3)可将工作空间中力转换为构型空间中的力和力矩。在此将机械臂上评估所受工作空间中引力与斥力合力的点称为机械臂控制点。显然,单一控制点无法满足机械臂各连杆的避障要求,故以DH法建系坐标原点及在其间插值设置多个控制点,控制点个数根据连杆长度而定,对各点进行引力斥力的合力计算后平移至对应关节末端,并将各连杆合力根据控制点个数求取平均值作为各连杆的最终受力,以应用于人工势场法进行路径规划。 人工势场法是一种虚拟力场法。其基本原理是将机器人在环境中的运动视为一种机器人在虚拟的人工势力场的运动。障碍物对机器人产生斥力,目标点对机器人产生引力,引力和斥力的合力作为机器人的驱动力,以控制机器人的运动方向和位置。但是该算法也存在一些问题: (1)机械臂控制点和目标点距离较远时,引力过大而斥力作用弱化,可能与障碍物发生碰撞。 (2)当障碍物和目标点距离较近时,斥力过大而引力作用弱化,导致目标不可达。 (3)在局部区域内某点引力和斥力大小相等方向相反时,算法易陷入局部最小值和局部震荡。 (1)重新定义引力斥力函数 本文以引力场为全局力场,斥力场为局部力场,建立新的引力斥力场函数,机械臂控制点所受引力与斥力分别为引力场与斥力场对距离的导数。 首先将引力场划界分为恒力场与变力场,建立引力场函数如下所示: (4) 式中,dL表示恒力场和变力场的边界距离;d(q,qgoal)表示控制点到目标点的距离;ξ表示引力系数,对应的引力函数为: (5) 如此可使机械臂与目标点较远时,受恒力牵引靠近目标点,解决距离过远导致所受引力过大问题;进入变力场后,随着靠近目标点,机械臂受引力逐渐减小至0。 设定斥力场函数时,在斥力势场函数中引入安全距离,以保证机械臂和障碍物之间的最小距离不会发生碰撞。建立的斥力场函数如下所示: (6) 式中,η表示斥力系数;D(q)表示当前控制点到障碍物点的距离;Q*表示斥力场的作用范围;k表示安全距离系数,安全系数的选取应大于等于0;Dob表示障碍物在某一个方向上的长度(球体为其半径长度;长方体为其各边长度一半)。 斥力场作用范围确定如式(7)所示: Q*=kQ·Dob (7) 式中,kQ为长度系数,其值应大于1。 对应的斥力函数为: (8) (2)特定距离下引力斥力关系设定 前文通过建立新的引力斥力函数,解决了机械臂距离目标点较远时引力过大而斥力作用弱化可能出现的碰撞问题。针对障碍物距离目标点过近导致的目标不可达问题,本小节在建立的引力斥力函数基础上,提出一种特定距离下的引力与斥力关系的设定方式。 首先设置某控制点所受斥力与引力关系: (9) 式中,ρ为该控制点处斥力相对引力的倍数。 然后设定控制点和障碍物距离与斥力作用范围之和比值如下: (10) 将Q*+kDob以x表示,式(9)可以表示为: (11) 将式(11)进行化简得到: (12) 根据式(12),即可求得特定距离下控制点所受斥力的大小,配合新建立的引力斥力函数,解决原算法目标不可达的问题。但需要注意,上式适用条件为: kDob (13) (3)局部最小值和局部震荡处理 人工势场法根据机械臂所受合力实现对其控制,当机械臂控制点在某一位置处所受到的引力和斥力之和为0时,即出现局部最小值问题;如果合力不为0而控制点在连续的两个位置所受合力方向相反时,则会出现局部震荡,以上两种情况都会导致机械臂难以到达目标位置。 人工势场法因其局部极小值问题导致目标不可达现象而限制了其应用。只有当虚拟目标点的引力场起到主导作用时才能有效脱离局部极小点位置。在此本文基于虚拟目标引力场,提出一种椭球模型策略来解决上述问题。 建立椭球模型首先建立椭圆模型:以障碍物中心为原点O;椭圆所在的平面由障碍物中心点、控制点及目标点确定。椭圆的长轴AB为控制点与障碍物中心点所在直线,椭圆的焦点F1F2为产生局部极小值或者局部震荡的控制点所在位置,建立椭圆模型如图4所示。 图4 椭圆模型 设椭圆的短半轴长度b=(1+k)Dob,椭圆长半轴根据椭圆的短半轴长度b和产生局部最小值或者局部震荡的控制点与障碍物中心点的距离c确定:若b (14) 若b≥c,则对a赋值为a=b,建立椭圆方程,此时椭圆成为圆形。将椭圆模型应用于三维空间时,需将其拓展为椭球模型,在此令椭球Z轴方向半轴长度值为b,建立椭球方程如下: (15) 建立方程后,分别计算控制点与障碍物中心点矢量e1,障碍物中心点与目标点的矢量e2以及矢量叉乘后的法向量n,通过e1、n即可建立椭球与机械臂基座之间的坐标变换关系。 局部最小值问题通过在椭球XOY面设立动态虚拟目标点处理。当机械臂陷入局部最小值陷阱后,在控制点所在椭圆焦点上方圆弧依次设定临时目标点并建立引力势场,当机械臂到达椭圆的近心点时视为已脱离局部最小值陷阱。当一个方向路径规划出现问题时,令机械臂原路返回至原焦点位置,反方向设置虚拟目标点,如图5所示。 图5 虚拟目标点示意图 机械臂初始关节角为[1.65 0.09 -1.76 -1.09 -1.68 1.31],目标物位姿[-0.35 -0.3 0.005 2.2 -0.64 0.34],在初始点和目标点之间随机位置设置几组障碍物,以验证改进算法下机械臂避障性能。设定实验参数ξ=500,η=10,KQ=0.9,k=1,ρ=5,限制各关节角步长π/90,实验仿真结果如图6~图9所示。 (a) 无障碍物路径规划 (b) 单障碍物路径规划 图6中机械臂分别在有无障碍物情况下由初始点至目标物进行路径规划。图6a中,机械臂在无障碍物情况下顺利到达目标位置。图6b中,虽设置障碍物但机械臂行进及避障搜索中未遇到产生局部最小值情况,因此两种情况下机械臂均以较平滑路径到达目标物位置。 在图7a中,设置多个障碍物,机械臂经过障碍物1进行避障时,由于合力作用,产生局部震荡情况,机械臂末端路径反复,难以跳出继续行进。基于改进算法下局部震荡解决策略,在图7b中,障碍物位置不变,机械臂在相同位置遇到局部震荡完成判定以后,迅速跳出局部震荡情况并在后续搜索中成功避开障碍物2,到达目标位置。本次规划中机械臂共设置13组控制点,运行共200步,对步数间隔提取,部分控制点与障碍物1、2的实时最小距离如图8所示。 (a) 发生局部震荡 (b) 跳出局部震荡 (a) 与障碍物1实时距离 (b) 与障碍物2实时距离 在图9a中,在目标物附近设置障碍物,机械臂靠近时,由于障碍物较大的斥力作用,机械臂反复震荡停滞不前,末端产生反复离散的路径点。在图9b中,障碍物位置不变,机械臂行进至目标物附近时,判断障碍物与目标物位置,根据特定距离下的斥力设定方式,使斥力相对减小,机械臂得以连续平滑的到达目标位置。以上图6、图7、图9所列几种情况的对比实验表明,改进人工势场法较好解决了传统算法缺陷,机械臂能有效完成三维空间的路径规划,满足规划过程中的避障要求。 (a) 目标不可达 (b) 目标可达 针对三维空间机械臂的路径规划,本文设计了一种改进的人工势场算法。将引力场作为全局引力场,斥力场作为局部力场,对引力斥力势场函数再定义;接着给出一种特定距离下引力斥力的设定方法作为辅助以解决障碍物离目标物过近时导致的目标不可达问题;然后设计一种基于椭圆模型的局部震荡跳出策略,以提高机械臂的路径规划能力;最后仿真结果表明,本文建立的碰撞检测模型能够对障碍物进行实时有效的碰撞检测。改进后的算法相比传统算法,对引力斥力的数值及作用范围进行不同情形下的多元设定更加合理,机械臂可根据不同问题快速判断并反应,通过设置动态虚拟目标点或更改障碍物斥力大小的方式,解决了局部震荡和目标不可达问题,满足三维空间中机械臂路径规划及避障要求。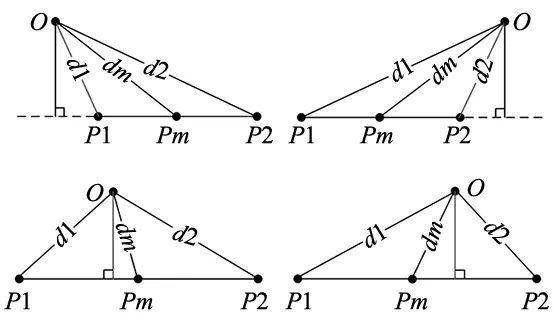
1.2 机械臂受力及控制点设置
2 传统人工势场法缺点与改进算法
2.1 传统人工势场法缺点
2.2 改进的人工势场法

3 仿真与分析




4 总结
