极端海况下单桩周围土体瞬时孔压响应分析

刘逸凡,刘红军,2*,刘 灿,潘光来

(1.中国海洋大学环境科学与工程学院，山东 青岛 266100；2.山东省海洋环境地质工程重点实验室，山东 青岛 266100)

引 言

基于Biot固结理论，Madsen[1]与Yamamoto[2]最早提出线性波浪作用下多孔弹性无限厚度海床土体的静力解析解，Hsu和Jeng[3]则进一步推出三维解析解。杨少丽等[4]计算得到了有关粉砂海床土孔压响应的有限差分解及极端风浪下的液化深度。王栋等[5]考虑了土骨架和孔隙流体加速度项，提出了适用于非均质土层及复杂边界条件下的有限元数值分析方法。漆文刚等[6]通过解析解计算了无粘性砂质海床土瞬时液化深度，并与Mory等[7]针对海洋结构物周围的瞬时孔压原位观测试验相验证。Okusa[8]、 ZEN[9]、Tsai[10]分别推导了一维、二维至三维等不同条件下的波致海床土瞬时液化判别准则，何影等[11]、叶建红等[12]对上述判别准则的液化区分布特征作出对比分析，并分析了各判别准则在海洋工程中的适用性。

有关单桩与海床相互作用方面的研究，李小均等[13]通过ABAQUS分析了桩体周围海床土体孔隙水压力响应，但模型中并无实质单桩，仅设置海床的桩土交界面处为不排水边界。该研究的不足之处在于将桩体的作用仅归结为一种接触属性的改变。胡翔等[14]在ABAQUS中进一步细化了单桩的属性参数，但作者并未将波浪荷载通过子程序以完整、连续的函数形式施加在海床表面，而是将动荷载分为数个分析步，以静力荷载的形式依次施加，该种加载方式在一定程度上会影响结果的准确性。朱斌等[15]综合考量了单桩及海床所受到的波浪力，对比了修正剑桥、运动硬化两种本构模型下桩周海床土的超孔压累积增长过程及液化分析，但文中桩体为小尺寸(1 m)实心方桩基础，弹性模量设置为30 GPa，类似混凝土性质，同时，其对单桩施加的波浪荷载为简化的集中荷载形式。

虽然以往学者对于残余孔压的累积增长过程有了一定研究，但对桩周土体瞬时孔压响应的研究仍相对较少。本文从极端海况条件出发，细化波浪与大直径单桩的相互作用过程，使单桩和海床分别同步受到来自波浪的水平和竖向荷载作用，分析在一个波浪周期内，单桩周围土体的瞬时孔压响应规律及瞬时液化的可能性。

1 数值模型与验证

1.1 数值模型参数

为分析波浪-土体-单桩三者之间的相互作用，在有限元软件ABAQUS中建立三维土体和单桩模型，其次将波浪以荷载的形式施加在单桩和土体表面。

参照海上风电大直径单桩实际尺寸建立单桩模型，其中长60 m，外径5 m，壁厚5 cm。参照钢管桩设置其物理、力学属性，其中密度为7.85 g/cm3，弹性模量为210 GPa，泊松比为0.2。按照C3D8R单元类型对单桩模型进行网格划分。

土体模型为半径50 m，厚50 m的圆柱体。本文研究对象为黄河三角洲区域粉质海床土，参照冯秀丽等[16]，贾永刚等[17]所研究的埕北浅滩区域地层物理力学性质参数，设置土体模型属性，其中土体湿密度为1.9 g/cm3，干密度1.5 g/cm3，泊松比为0.3，弹性模量为3.5 MPa，内摩擦角为30°，粘聚力为20 kPa，采用摩尔库伦本构模型表示。设置土体孔隙比为0.8，孔隙水容重为10 kN/m3,渗透系数为10-6m/s，土体模型整体属性保持一致。土体网格单元类型为C3D8P(八节点六面体位移孔压耦合单元)。单桩入土深度为30 m，桩土接触属性采用法向硬接触，切向摩擦系数设置为0.3。

单桩与土体数值模型尺寸及网格划分如图1所示。

1.2 荷载边界条件

首先为单桩和土体模型设置初始应力状态：对单桩和土体模型施加重力荷载，同时为土体设置初始应力场以平衡地应力；设置土体初始孔压场为零，限制土体侧面和底面位移。

海上风电单桩基础及周围土体所受到的荷载包括：

荷载一：上部风机结构自重对单桩基础产生的竖向荷载。本文参照5 MW风机结构重量为500 t，设置竖向荷载为5 MN，以集中荷载的形式施加在单桩顶部表面。

荷载二：海床表面受到的波浪竖向荷载作用。其随波面起伏不断变化，已知波浪表面方程如式：

η=αcos(kx-ωt)

(1)

式中，η为波面位置；α为波幅；x、t为波浪的水平位置及时间；k为波数；ω为角速度。

结合随水深的波浪衰减系数，得到作用在海床表面的动波压力如式(2)，该式为净波压力，不含静水压力。

(2)

式中，P0为波压力；ρ为水体密度；h为水深；H为波高。式(1)(2)以水面为基准面。

与陆地上土体表面受到的压力不同，波浪对海床表面不仅有波压力作用，同时赋予海床表面相应的孔隙水压力边界，该孔压边界值与波压力值一致，同样采用式(2)设置。根据土体内不同位置的孔压分布，可以判断孔隙水在土体中的渗流方向。三维海床泥面上所受到的波压力按式(2),作为X轴方向上位置和时间的函数施加在单桩基础周围，因表达式(2)并未表现单桩的影响，因此土体表面所受波压力与波浪遇到单桩产生的反射和绕流现象无关，更多地体现的是桩土接触面带来的影响。上述竖向波浪荷载及孔压边界条件以子程序的形式在ABAQUS中添加。

荷载三：单桩受到的波浪水平荷载作用。本文以线性波形式，采用莫里森方程计算波浪力。以往的研究中针对该水平荷载多以集中力的形式[18]施加在桩顶刚片上，表达式如式(3)所示。但该式为积分方式计算得到的集中力荷载，同时对式(4)中的参数进行了近似和简化，从而忽略了波面起伏、水深等因素对波浪力的影响。

(3)

(4)

式中，FH为集中力荷载；D为单桩直径；CD和CM为拖曳力系数和惯性力质量系数，分别取1.2和2.0[19]；θ表示kx-ωt。

所研究极端海况取自黄河三角洲海域50 a一遇[20]的波浪条件，其具体波浪参数为波高6.7 m，波长77.4 m，周期8.6 s，单桩所处位置水深假设为10 m。

对于极端海况下的波浪，不仅波浪周期长，同时具有大波高，使得波峰与波谷时刻水面位置相差较大，且持续时间较长。为更好地体现一个周期过程中，波浪对单桩产生的水平荷载变化，本文根据莫里森方程[21]得到水中某一深度处单桩受到的波浪力原始表达式，如式(5)。

(5)

(6)

式中，fH为分布式荷载；ux为水质点速度；z为计算水质点至海床表面的距离。

对于该表达式，首先是有关波浪的函数，受波浪运动到单桩时的相位时刻、单桩所处的水平位置影响，其次同样受到单桩的影响，根据波面起伏位置确定单桩受力范围。因而，本文通过ABAQUS荷载自定义子程序，基于有限元原理，将该表达式所述荷载对应施加在单桩表面所有深度位置处；最后设置条件函数，保证单桩只有位于水中的部分受到波浪水平荷载作用。如此，则单桩表面受到的水平波浪力可以随着波面的起伏而不断变换作用范围与作用大小，同时波浪相位与海床所受波浪相位始终保持一致。其中部分子程序如图2所示。

图2 单桩所受波浪力的子程序部分

根据荷载条件共设置三组计算方案，分别是：

(1) 对照方案，在不含单桩的土体模型上施加波浪荷载二；

(2)方案一，对单桩-海床体系施加荷载一和荷载三，观察单桩前后运动对桩周土的影响；

(3)方案二，在方案一基础上，再对体系施加荷载二，观察波浪的水平与竖向荷载共同作用下桩周土孔压分布。其中方案一与方案二的荷载示意图如图3所示。

1.3 本文数值模型的验证

针对波浪作用下海床土体内孔隙水压力响应，参照以往研究中Hsu和Jeng[3]提出的解析解、Liu和Jeng[22]得到的试验结果，在相同的波浪、土体条件参数下计算本模型的数值结果。将所得的三组数据绘制曲线如图4所示，通过分析波致孔压(相对)最值随相对入土深度的变化，可以发现本文所使用的数值模型计算结果与以往学者得到的解析解数据和试验数据结果具有较好的吻合性，验证了本文数值模型计算方法的可靠性。

2 计算结果分析

2.1 未受单桩影响处海床孔压响应

为观察单桩对海床土孔压响应带来的影响，首先仅对波浪作用下的海床土体(不含单桩)孔压响应进行分析，以更好地与后期(包含单桩结果)进行对比。如图5所示，波浪运动到该位置时为波谷状态，因而首先出现负孔隙水压力，之后随时间呈周期性变化。如图6所示，随着深度的增加，孔压峰值在有规律地递减，以波峰时为例，由海床表面处的26.7 kPa降低至30 m处为3.2 kPa。

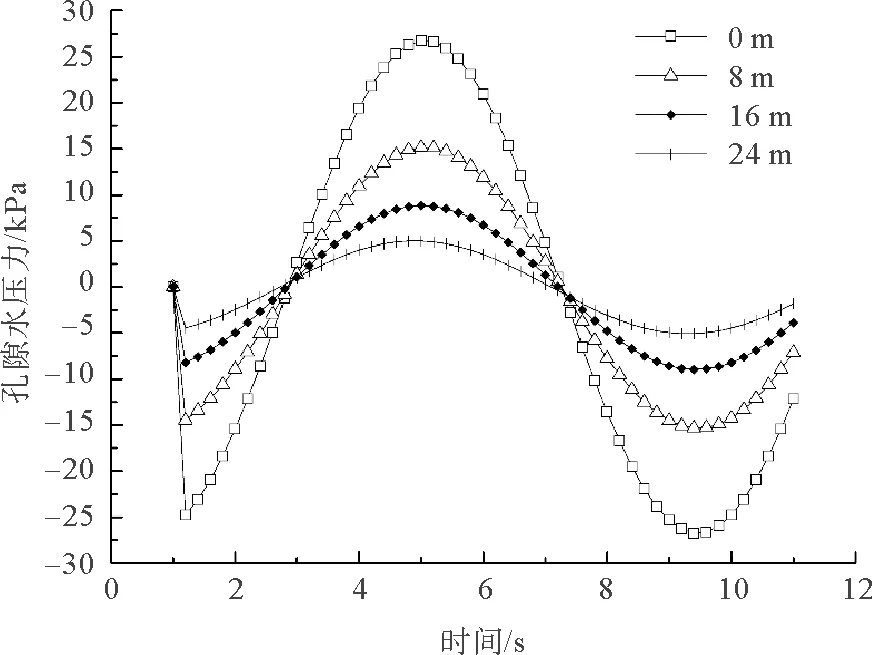
图5 不同深度处海床孔压随时间变化曲线

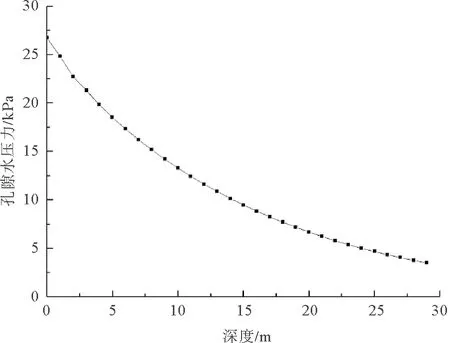
图6 孔压峰值随深度变化曲线

2.2 仅受波浪水平荷载影响下桩周孔压响应

在方案一中，输出桩后不同深度处土体的孔压变化曲线如图7所示，水平位移随时间变化曲线如图8所示，作用时间为一个波浪周期。以20 m土深处为分界点，单桩绕该位置随波浪发生前后运动。将图7与图8对应分析可得，随着单桩的运动，当某一时刻土体受到桩体压力作用，发生正向位移时，此时该部分土体呈现出正孔隙水压力；若土体受到桩体拉力作用，出现负位移时，此时土体内呈现负孔隙水压力。

图7 桩后不同深度土体孔压随时间变化曲线

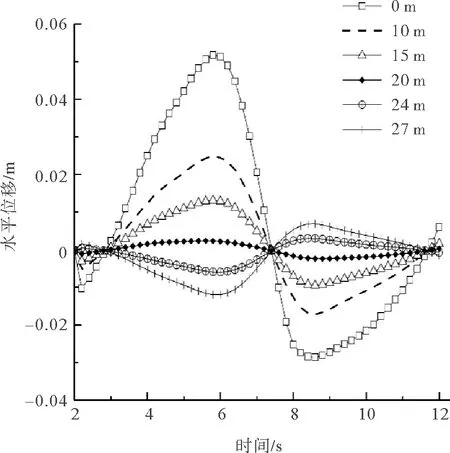
图8 桩后不同深度土体水平位移随时间变化曲线

2.3 波浪水平与竖向荷载共同影响下桩周孔压响应

在方案一的基础上施加海床表面波浪荷载，得到方案二。已知对于周围土体而言，单桩的存在类似于一种边界限制，一方面阻碍了波浪竖向荷载作用下周围土体的水平位移幅度，使得桩周土的孔压变化相较于图5出现较大改变；另一方面则受单桩的水平运动影响，如2.2所示。两种作用效果相叠加后，得到桩后土体的孔压分布曲线如图9所示。如图9(a)所示，对于1～8 m深度范围的土体，其孔压峰值绝对值，均超过了表面海床孔压峰值，维持在30～50 kPa之间，其中负孔压峰值接近-50 kPa，出现在时间轴的10 s位置附近。随着深度的增加，在2～8 s内，观察到孔压曲线逐渐向负孔压方向靠拢，并在一个波浪作用过程中观察到在13～20 m深度范围内，土体内均为负孔隙水压力。对比图9(a)与图9(b)，可以发现随着深度增加，孔压幅值不仅大幅波动，相位同样出现明显的变化。

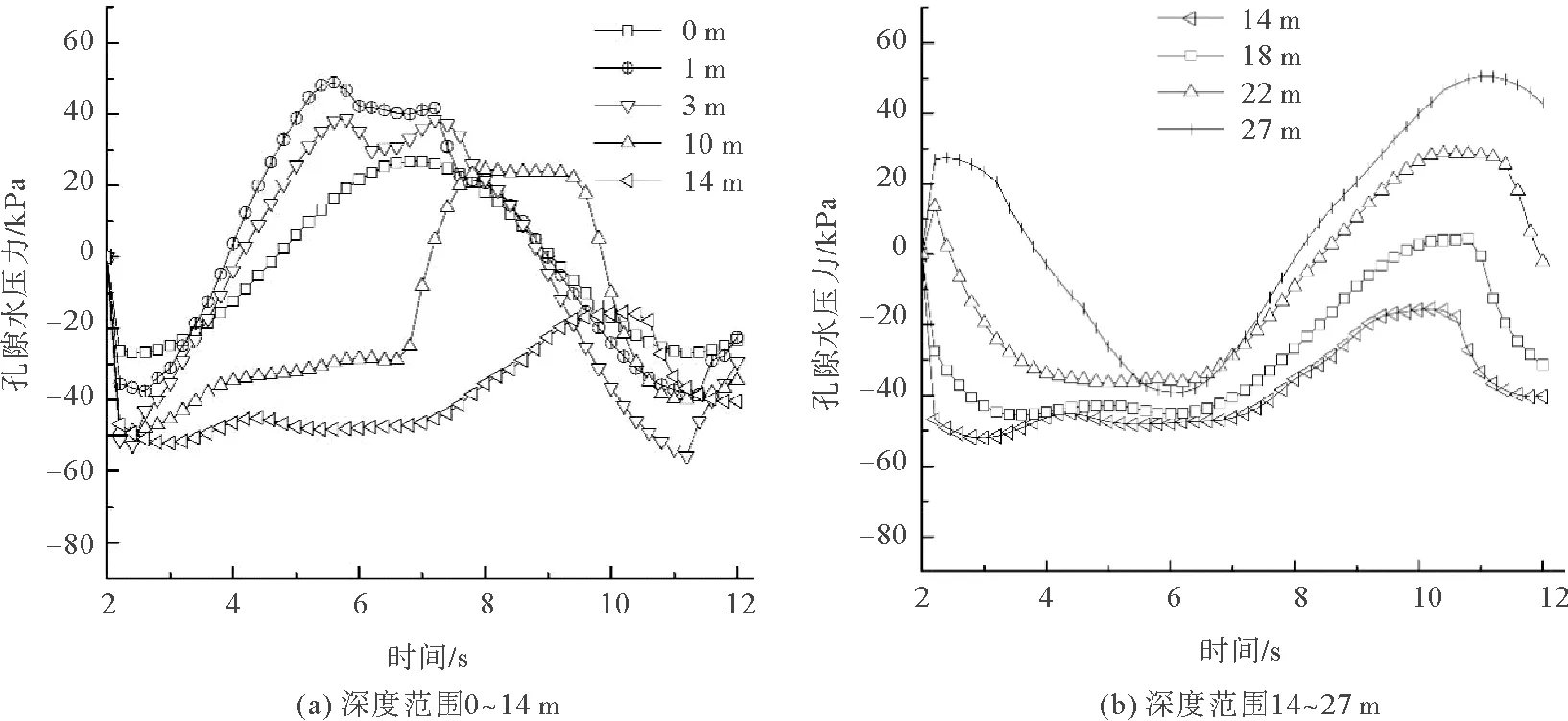
图9 桩后不同深度土体孔压随时间变化曲线

同样的方法输出桩体前侧的土体孔压分布，其整体分布规律与桩后土体一致。如图10(a)所示，桩前土体的负孔隙水压力可达-83 kPa，远小于桩后土体相同深度位置的负孔压(-50 kPa)；如图10(b)所示，在桩土交界面(30 m)深度位置，桩周土孔压呈现明显的波动增加，随着远离单桩底面，孔压曲线则逐渐趋于平稳。

图10 桩前不同深度土体孔压随时间变化曲线

2.4 不同计算参量对桩周孔压响应的影响

如表1所示，以增加单桩的稳定性为出发点，分别从土体的弹性模量(依据已有勘察数据，大幅提高土体弹性模量)、单桩入土深度、单桩顶部所受竖向荷载等角度出发，研究计算参量改变对单桩周围土体内孔压分布的影响。

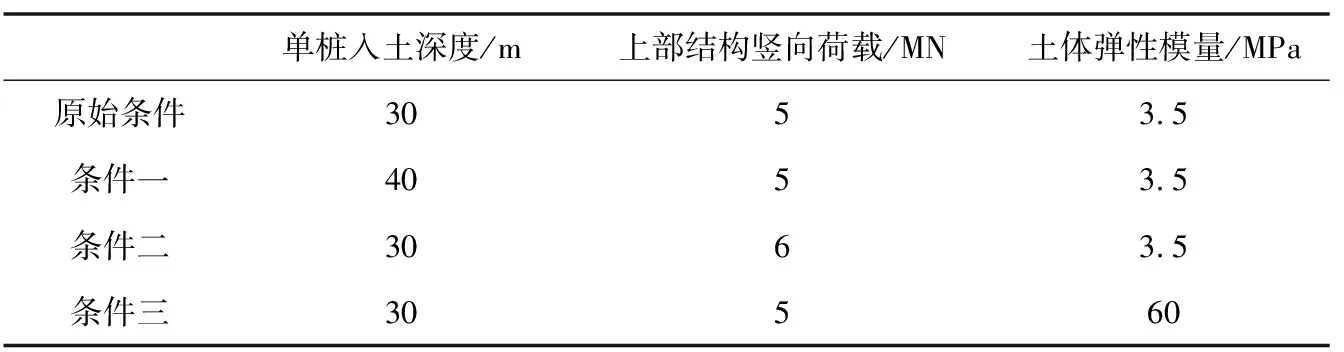
表1 不同变量条件下的参数设置

采用方案二进行计算，取单桩后侧土体孔隙水压力峰值为研究对象，绘制出不同条件下其沿深度的分布曲线，如图11所示。

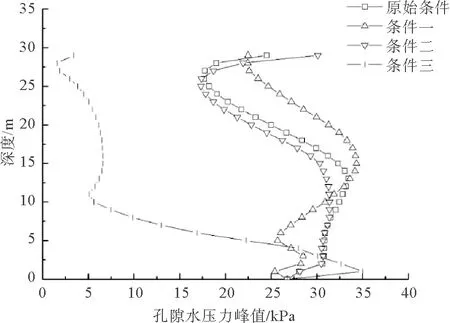
图11 不同条件下桩后孔压峰值随深度变化曲线

以图中原始条件曲线为对照组。如条件一所示，随着单桩入土深度的增加，使得土体对单桩的约束作用加强，表层深度范围桩周土体的水平位移幅值减小，从而使得该部分土体孔隙水压力有所降低；如条件二所示，上部荷载的增加对整体深度范围内土体的孔压均带来一定降低效应，且孔压分布规律未受影响，可见在单桩基础已有的自重条件下，不同功率参数的风机带来的上部结构重量差异相比于基础结构的自重比例较小，因而在条件二下孔压分布变化并未出现十分显著的变化；如条件三所示，当增大土体弹性模量后，土体孔压的降低幅度最大，在10 m深度范围内降低了约25 kPa，可见弹性模量的增加在提高土体强度、减小周围土体运动幅度上具有重要作用，进而对孔压的累积表现出一定的抑制效果。

2.5 桩周土体瞬时液化分析

根据Zen等[9]所提出的液化判别准则，当波浪作用下土体内部的孔隙水压力与土体表面的孔隙水压力之间的差值所形成的向上的“超静孔隙水压力”，大于初始状态下的土体有效自重时，上部的土体便会发生瞬时液化。具体表达式如下：

(P-P0)≥γ′z

(7)

式中，P表示波浪在深度为z处的土体位置产生的孔隙水压力；P0表示同样水平位置处海床表面的波致孔隙水压力；γ′表示土体的初始有效容重。

根据判别准则，瞬时液化应当出现在波浪的波谷作用时，此时土体内的渗流力方向向上。如图12所示，分别输出桩周土体的初始自重应力以及超静孔隙水压力随深度的变化曲线。根据式(7)，判断桩体前侧土体瞬时液化最大深度可达160 cm，桩后土体液化深度最大为90 cm。随着与单桩距离的增加，土体的液化深度范围明显降低，以距离单桩外表面2 m水平距离为例，此时桩前土体液化深度范围降低为85 cm，桩后土体则降低至50 cm。

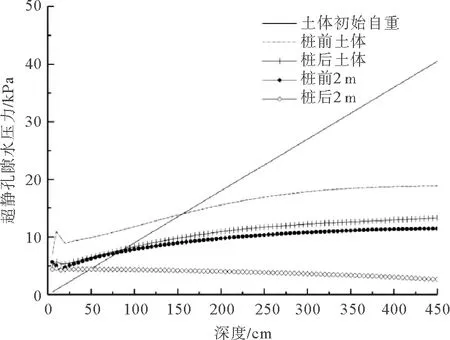
图12 桩周不同位置土体超静孔隙水压力随深度变化曲线

3 结论

本文通过ABAQUS子程序的方式细化了海床与单桩所受到的波浪荷载作用，其中单桩受到的水平波浪荷载能够随波面的起伏而改变作用范围，与海床表面受到的竖向荷载保持同相位，与实际情况更接近，从而分析了极端海况下单桩基础周围土体瞬时孔压响应。

单桩基础的存在使得周围土体的孔压分布在幅值和相位方面均发生巨大变化。单桩的前后运动会影响周围土体的水平位移，从而生成相应的正负孔隙水压力。土体弹性模量、单桩入土深度的增加均能有效降低表层深度范围内土体的孔压峰值水平。桩周土体的瞬时孔压分布具有不对称性，可见在波浪的水平作用下，单桩的前后运动对海床土原有的孔压响应机制产生了较大影响：在波浪的水平作用与竖向作用保持相位一致的情况下，结合2.2中单桩前、后水平位移幅值可以发现，相比于向后运动，单桩向前运动幅值相对更大，对周围海床土体孔压响应产生的影响也更明显。因此，在波浪的水平与竖向共同作用下，桩前土体的负孔隙水压力峰值明显小于桩体后侧，使得前者的超静孔隙水压力明显大于后者，从而使得桩前土体的最大瞬时液化深度超过桩体后侧土体。同时，瞬时液化深度范围随着远离桩体而有所降低。

本文的研究尚有一定不足，如波浪以荷载形式的方法施加尚不能描述波浪沿单桩绕流的影响，因而本文并未对桩体侧面的土体响应展开分析。后续的研究会继续深入波浪流体性质方面的研究，进而更好体现波浪-桩-土三者的相互作用。