规则波与直立堤相互作用的数值模拟

2022-06-29王艺之韩新宇

海洋湖沼通报 2022年3期

王艺之，韩新宇，董胜

(中国海洋大学工程学院，山东青岛 266100)

引言

在海岸工程中，防波堤发挥着维护港池稳定、保障港内生产工作平稳进行、保护生态岸线等重要作用，因此对防波堤迎浪面所受的波压力也得到了广泛的研究。防波堤一般分为混合堤、直立堤、特殊型式三种，其中直立堤是建立最早、应用最广泛的防波堤型式。

1963年侯穆堂和李玉成[1]通过物理试验对直立堤上的波压力进行了研究，他们将直立堤前的波浪分为立波、破碎波、过渡波三种形态，并对其中破碎型波压力的计算进行了研究。随后他们又研究了堤前破碎波的特征及其对混合堤和直立堤的作用[2]，提出破碎波压力分布呈上大下小，且在静水面处产生最大波压力。Kirkgöz[3-6]从1992年到2005年期间对直立堤和斜坡堤上波浪破碎的荷载进行了一系列的研究，分析了堤前相对水深、堤前波浪形态、等因素对波浪作用力的影响，并提出了一种计算直立堤上破碎压强的理论方法。他还提出，当垂直波面冲击到混合堤上时，将造成最大波浪荷载。Yu等[7]研究了直立堤在斜向波作用下的水力学特性以及堤上波浪力的分布规律，并分析了波浪方向、波陡以及波浪的不规则性对直立堤所受波浪力的影响。

随着科技发展，数值模拟由于具有节省人力物力、计算效率高、后处理方便等优势，得到了迅速发展，产生了多种多样的求解方法，并在波浪与海工建筑物相互作用方面也得到了广泛的应用：黄蕙等[8]利用加源项造波的方法探究了波浪与涵洞式削角直立堤的越浪、透浪情况；李东洋等[9]基于OpenFoam开源软件模拟了不规则波作用下扭王字块护面斜坡堤的越浪过程；李昌良等[10]利用Ansys-Fluent软件模拟了规则波与透空防波堤的相互作用，并讨论了防波堤和波浪要素的变化对透空防波堤透射系数的影响；谢海清等[11]利用FLOW-3D软件模拟了狭窄库区河道滑坡涌浪产生及传播过程，并对最大涌浪高度及其沿程传播衰减规律进行了公式拟合；李晶晶等[12]利用格子Boltzmann方法对土石混合体的渗流场进行了模拟，并对其渗流特性进行了分析。

在利用数值模拟方法求解CFD问题时，常用的方法可以分为网格法和无网格法两大类，其中，网格法主要包括有限差分法、有限体积法、有限元以及边界元等，无网格法主要包括光滑粒子法(SPH)以及格子Boltzmann方法(LBM)等。本文使用的模拟方法，分别选取利用网格法中有限差分法求解为基础的FLOW-3D，以及利用无网格法中LBM为基础的XFLOW软件进行数值模拟，探讨这两种软件在模拟波浪对直立堤波压力问题上的准确性，并选择其中较为准确的方法进一步模拟，讨论直立堤上波浪力随入射波周期增大时的变化。在进行数值建模时，两种模型均采用推波板造波、斜坡消波，并在防波堤附近进行网格加密或粒子细化。本文分别对两种水位下、波峰和波谷分别作用时的波压力进行了分析，并与于龙基论文中提供的实验数据[13]进行了对比，所得结论对防波堤设计有一定参考价值。

1 数值模型

基于无网格法中LBM的数值模拟软件XFLOW，其控制方程为BGK逼近下的格子Boltzmann方程：

(1)

式中，f=f(x,ξ,t)是单粒子分布函数;ξ是微观速度;λ是与碰撞有关的松弛时间;feq是平衡分布函数。

基于网格法中有限差分法的数值模拟软件FLOW-3D，使用FAVOR网格处理技术以及VOF自由表面捕捉方法，达到精确定义几何外形以及自由液面模型的效果。其控制方程为如下：

连续性方程：

(2)

N-S方程：

(3)

(4)

(5)

式中，u、v、w分别是x、y、z方向的速度；Ax、Ay、Az分别是三个方向的流动面积分数；Gx、Gy、Gz分别是三个方向的重力加速度分量；fx、fy、fz分别是三个方向对应的粘滞力加速度；VF为体积分数；ρ为流体密度。具体原理可以分别参考文献[14,15]，此处不再赘述。

2 数值模拟

2.1 数值模型设定

2.1.1 XFLOW数值模型设定

在XFLOW中建立二维水槽，长度为20 m，高度为1.2 m，防波堤与推板中心之间的水平距离为5.0L(L代表入射波波长)，在水槽末端设置消浪斜坡以达到消浪的效果。为提高计算效率，本文选取粒子间距为2.0 cm，仅在自由表面上下总高度约一个波高的矩形范围内以及整个防波堤附近进行自适应粒子细化至1.0 cm。模拟时长为30 s。

2.1.2 FLOW-3D数值模型设定

在FLOW-3D中建立长度为20 m、宽度为0.5 m、高度为1.2 m的三维水槽，并将其划分为三段：推板至防波堤迎浪面前约1倍入射波长处(记为A点)为造波段；从A点至防波堤后1 m处(记为B点)为试验段；从B点至水槽末端为消波段，消波段放置消浪斜坡以达到消浪的效果。为保证试验结果的准确性，同时提高计算效率，对造波段和试验段中波高范围内的网格，以及试验段中压力测点高度范围内的网格进行加密，由于缩尺后波高为182.5 mm，且波高范围内包含不少于10个网格，故加密范围内网格边长不大于18.25 mm，其它部分网格边长约为25 mm。防波堤与推波板的相对位置根据率波情况确定，放置点率波结果应与目标波高基本吻合。模拟时长同样为30 s。

2.2 工况设定

共设两种水位，分别为极端高水位(水深22.62 m)和设计高水位(水深21.88 m)，波高为7.3 m，波周期为8.9 s。在进行数值模拟时，对原模型进行缩放，取长度比尺为λl=40，时间比尺为λT=401/2，压强比尺为λp=40，压力比尺为λF=403。断面尺寸如图1所示，(断面尺寸按照原型尺度标注，单位：mm)。在防波堤迎浪面布置压强测点，其中A1—A6位于防浪墙上(A2位于设计高水位，A3位于极端高水位)，C1—C5位于沉箱段。以直立堤迎浪面为y轴，防波堤底面为x轴，测点坐标如表1所示(坐标尺度为缩尺后的尺度，单位：mm)。对应的物理模型在长50 m、宽1.2 m、深1.2 m的水槽中进行，模型按照重力相似准则进行设计，模型缩放比例与数值模拟所用比尺相同，用于对比的波压力试验数据来自于文献[13]。

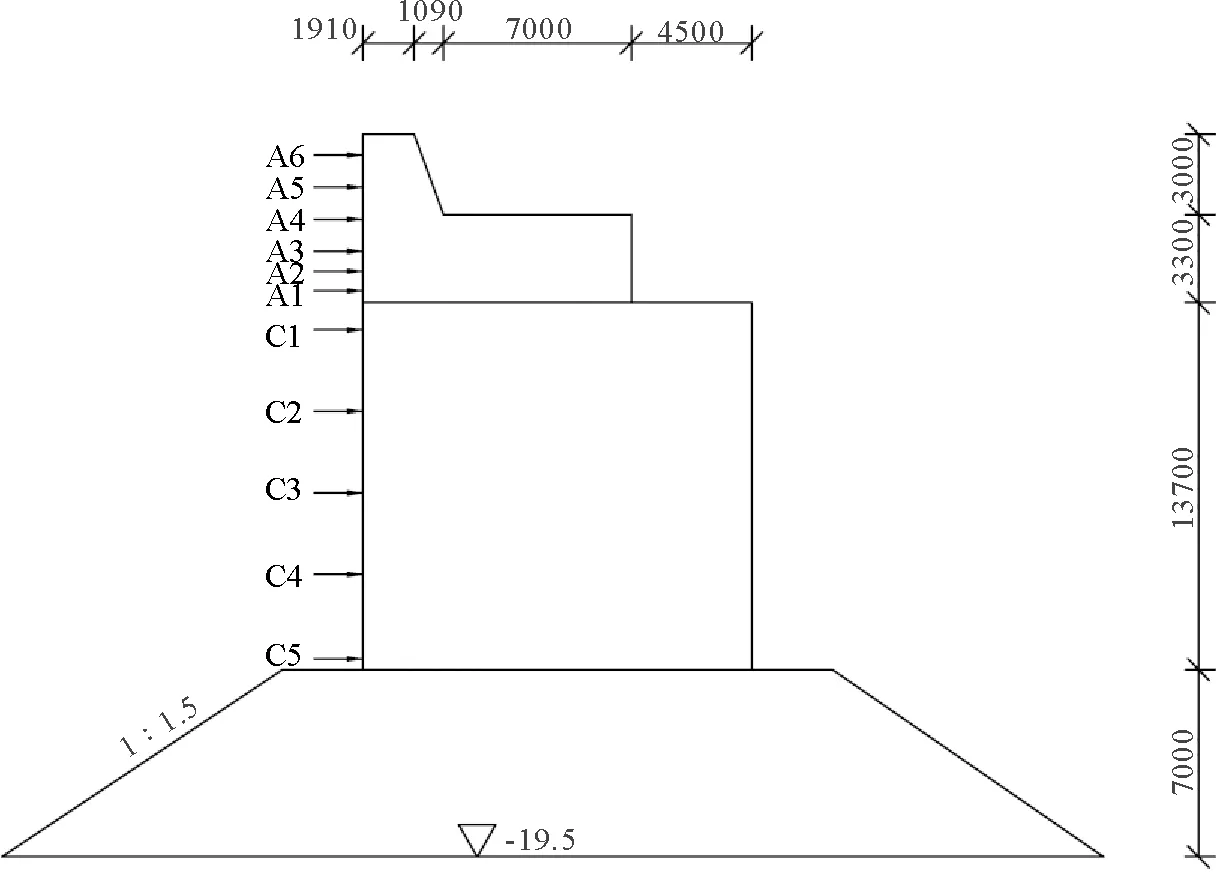
图1 防波堤断面及测点示意图

表1 测点坐标

在研究波压力随入射波周期变化情况时，增设110%T、120%T、130%T和140%T四种周期，与两种水位共组合出十种工况进行计算。

2.3 数值造波及验证

根据文献[16]中的波浪理论的适用范围，本文波浪采用斯托克斯二阶波进行模拟比较合适。Madsen于1971年提出斯托克斯波的推板运动公式[17]，对于二阶波，波高、波长和水深应满足HL3/d3<8π2/3的条件，推板的运动方程可以表示为：

(6)

相应的推板速度方程为：

(7)

以极端高水位为例分别对数值水槽进行率波，验证造波效果。得到的对比结果如图2所示。两种方法得到的波形和波高都能较好地与理论波形吻合。

图2 数值造波与理论波形对比

3 基于数值结果的分析和讨论

3.1 迎浪面压力与试验结果对比

图3给出了分别在波峰和波谷作用下两种不同的数值模拟方法得到的各测点波压力与试验结果[13]的对比。横坐标为波压力，纵坐标为测点坐标，横、纵坐标均还原为原型尺度。从图中可以看出，波峰作用时，最大波压力发生在静水位附近，在防波堤设计时应考虑对静水位附近进行加固。总体来说，两种方法得到的压力曲线均与试验结果趋势一致，吻合较好。

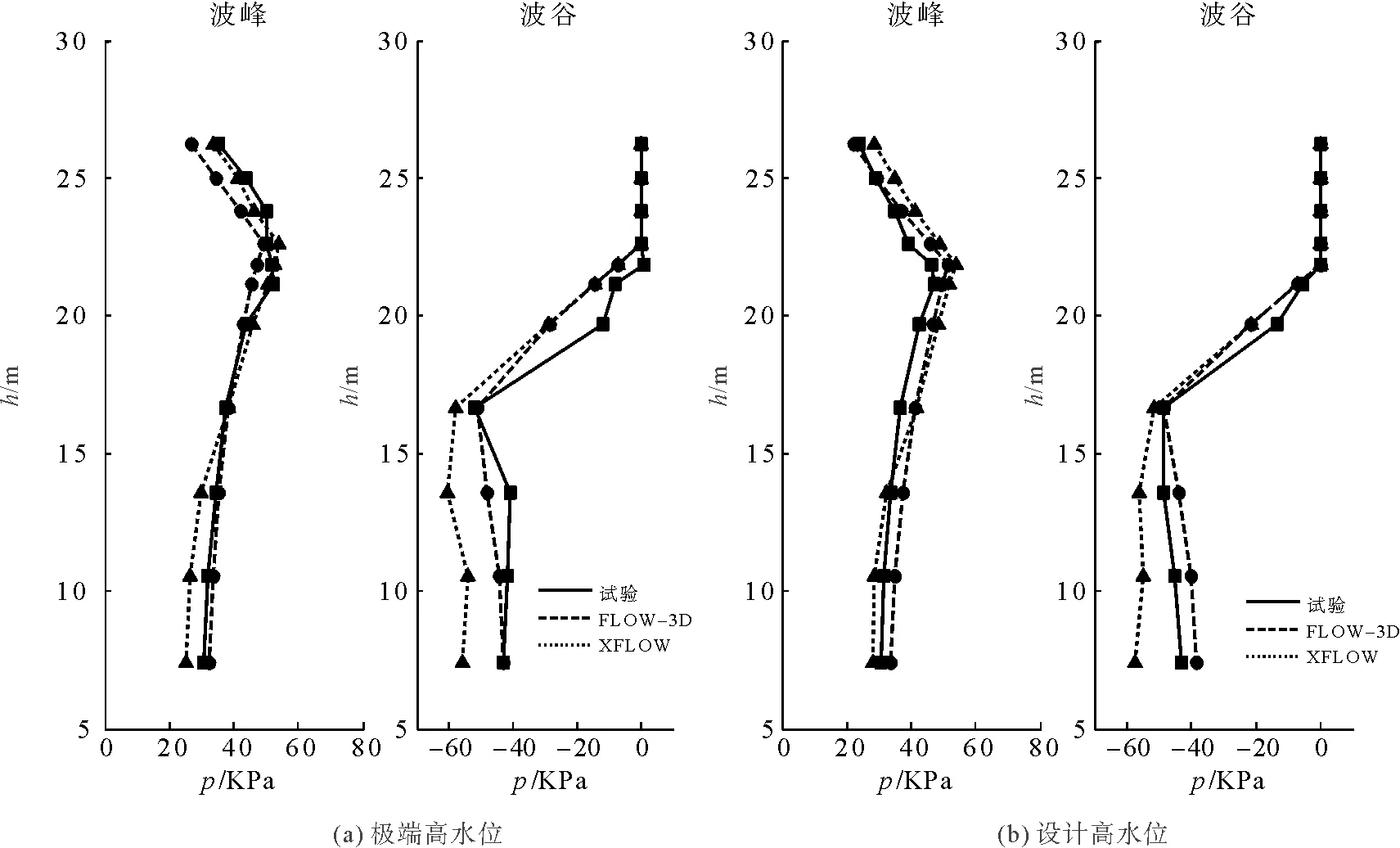
图3 两种数值模拟结果与试验结果对比

从计算过程来看，两种模拟方法各有利弊。基于无网格法的XFLOW的优势是可以并行计算，且测点位置可以在后处理时设定，只需计算一次即可得到该参数下任意测点的结果，但其计算时间较长，无法较快地得到反馈并对模型进行调整；基于网格法的FLOW-3D的优势是计算速度快，能够比较快地得到反馈，及时调整模型，但它需要在计算之前对测点地位置进行设定，只有设定好的测点能够得到结果，一旦该测点需要调整位置就需要对整个模型重新计算。两种方法共同的优势是可以对特定区域的网格进行加密或者自适应细化粒子，显著提高了计算效率。

从计算结果来看，分别对四种情况下防波堤整个迎浪面的波压力进行积分，并计算其与试验结果的误差，具体误差如表2。从表中可以看出，针对本文的模型，FLOW-3D数值模型的误差除设计高水位下波峰作用时略大于X-FLOW数值模型以外，其它工况下的误差均小于X-FLOW数值模型，且整体的平均误差也相对较小。因此对于本文模型，FLOW-3D能够得到更好的模拟结果，故在研究波压力随入射波周期变化情况时，选用FLOW-3D数值模型进行计算。

表2 两种模拟方法所得波压力的误差

3.2 迎浪面压力随周期变化情况

图4给出了沿高程分布的测点的波压力分别在波峰、波谷作用下，随周期变化的情况。从图中可以看出，随着入射波周期的增加，波峰作用时压力最大点出现在静水位附近，各测点波压力均有增长，增幅均匀减小，极端高水位下当周期达到120%T后以及设计高水位下周期达到130%T后，各测点波压力随周期变化增幅极小；波谷作用时，C2测点以上各测点露出水面，故压力基本一致，未发生变化，C2测点以下各测点压力均有所减小，且从110%T开始各测点波压力较为稳定，随周期变化的幅度极小。