液体运载火箭线性自抗扰容错姿态控制方法

魏远明， 罗亚中， 朱海洋

（1.国防科技大学空天科学学院， 长沙 410073； 2.北京宇航系统工程研究所， 北京 100076）

1 引言

中国航天的飞速发展对运载火箭发射成功率提出了更高要求。 为了有效提升成功率，主要采用以下2 种措施：①进一步提升运载火箭可靠性，从单机、系统和总体3 个层级提升整体可靠性设计水平；②使用新技术，如故障诊断和容错控制技术，提高运载火箭在故障下的适应能力，进而提升任务成功率。

尽管目前发动机组件采取了冗余设计，可靠性大幅提高，但其失效对火箭而言是不可接受的。 通过故障诊断和控制重构算法，可利用其余正常工作的发动机和伺服机构来补偿故障，保证正常入轨或减小入轨偏差。 针对发动机故障，主要有2 类解决方法：①先进行故障诊断，后进行控制重构，即通过发动机直采的力热参数在线辨识进行故障诊断，得到相应故障信息，尤其是发动机推力下降比例，进而重构姿态控制算法；②无需故障诊断，仅通过鲁棒自适应性强的控制器进行辨识或有效补偿。 朱海洋等针对发动机故障，提出了基于径向基神经网络自适应的容错控制方法，使用径向基神经网络在线辨识故障参数并补偿，有效解决了故障下的姿态控制稳定和精度问题，但是该方法只针对刚体火箭，不适用于具有复杂刚晃弹特性的液体运载火箭。

对于具有复杂刚晃弹特性的大型液体运载火箭，容错姿态控制应该考虑在保证箭体弹性振动和推进剂液体晃动稳定的同时，尽可能提升刚体动力学控制效果与性能。 目前国内外对于液体运载火箭姿态控制成熟方法均为PD＋校正网络控制器，其在有限偏差包络内的控制效果是稳定的，尤其是校正网络环节对惯组速率陀螺等传感器信号的整形滤波作用，有效地保证了弹性振动和推进剂液体晃动稳定。 为有效提升控制器容错性，在传统控制器基础上添加补偿控制是研究应用重点方向之一。Orr 等提出了基于传统控制器的自适应增广控制方法（Adaptive Augment Control， AAC），在故障工况下可自适应调整开环增益来适应故障，但基于传统PD 控制器，并未改变控制器结构，所以无法补偿故障影响并消除偏差。

本文针对液体运载火箭常见的发动机故障，开展容错姿态控制技术的研究。 借鉴自抗扰控制思想，在基线PD＋校正网络控制器基础上，提出一种基于扩张状态观测器的线性自抗扰控制方法（Linear Active Disturbance Rejection Control，LADRC），该方法使用线性扩张状态观测器来观测并补偿回路总和扰动，通过时域仿真，与PD＋校正网络、自适应增广控制方法对比，证明方法的有效性。

2 研究对象及动力学模型

2.1 研究对象

本文以某型新一代运载火箭助推飞行段为例，其助推段发动机布局如图1 所示。

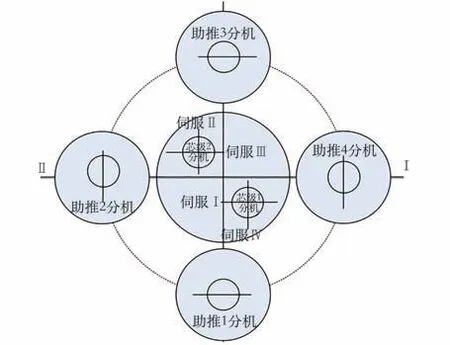
图1 一级发动机布局Fig.1 Layout of the first stage engines

2.2 火箭动力学模型

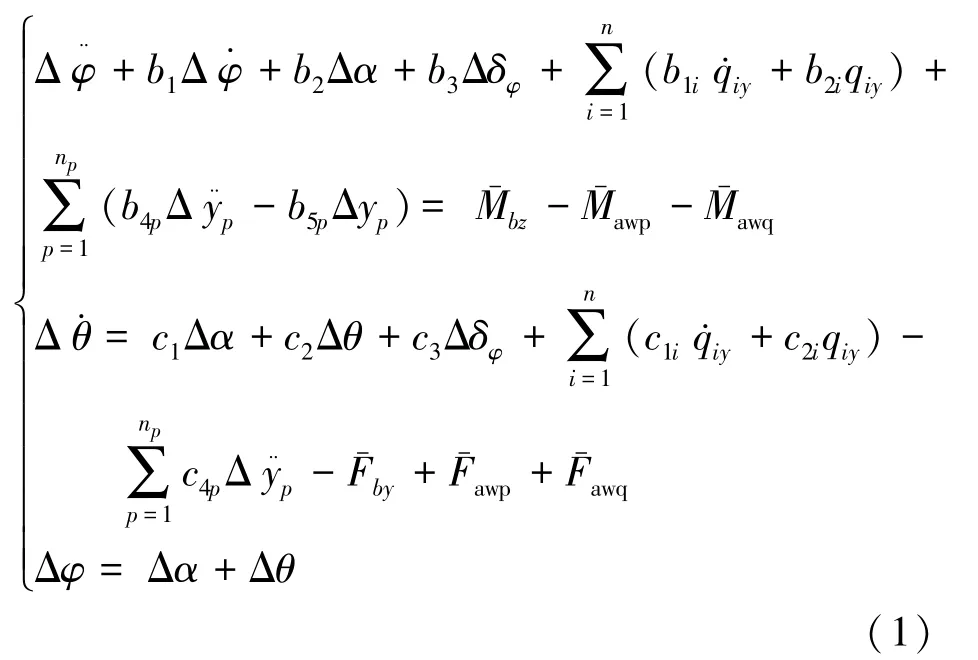
考虑推进剂晃动和箭体弹性振动，以俯仰通道为例，液体运载火箭一级飞行段姿态动力学线性模型如式（1）所示：

俯仰通道弹性振动方程如式（2）所示：

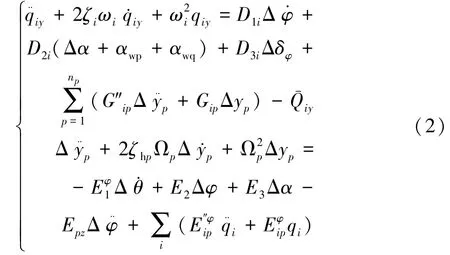
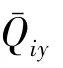
由式（1）、（2）可进一步建立表征运载火箭姿态动力学的广义模型，实际可控动力学模型可表示为式（3）：

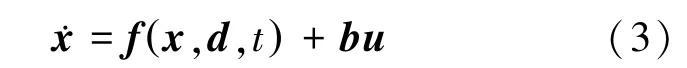
式中，为模型状态向量；为表征外界干扰和未建模动态特性项；（，，）＝［（，，），（，，），（，，）］为俯仰、偏航、滚动通道中除输入量之外的总和扰动项；＝［，，］为俯仰、偏航、滚动通道的控制力矩系数矩阵；＝［Δδ，Δδ，Δδ］为俯仰、偏航、滚动通道的控制输入向量。

用通用模型表示的运载火箭姿态动力学模型如式（4）所示：

式中，，为偏航角及角加速度，，为滚转角及角加速度，为弹道偏角，为侧滑角。

3 传统PD 控制方法与自适应增广控制

3.1 传统PD＋校正网络控制方法

对于液体运载火箭，传统控制方法为PD＋校正网络控制方法，以俯仰通道为例，反馈控制方程如式（5）所示：

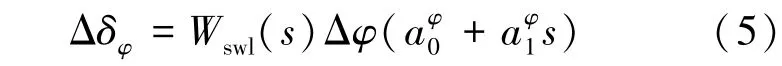
3.2 自适应增广控制

采用Orr 等的自适应增广控制改善传统控制性能，算法核心思想是通过变增益使系统性能在动态性能和稳态性能之间调整，以适应当前工况，基本设计目标为：①仅在非标称条件下才调整增益，标称情况下不改变增益，从而不影响传统控制方法的性能；②刚体误差较大时，调大增益，提高系统动态性，而在控制－结构耦合严重的工况，降低增益，提高系统的稳态性；③在发生严重故障或者出现其他恶劣工况时，AAC 系统可防止或者延缓系统失控发散。

3.2.1 开环回路

开环回路增益表达式如式（6）所示：

式中，为开环回路增益，的上、下限可以从标称系统模型的经典增益裕度确定；为自适应增益的初始值；k为增益的自适应项，如式（7）所示：

式中，为自适应误差增益；为频谱阻尼器增益；为溢出增益；（－k）为逻辑阻尼项；ae为误差项，用以解决刚体误差问题，调大增益，提高系统动态性能；－αky为频谱阻尼器输出，用以解决控制－结构耦合问题；－（－1）为溢出项，用以防止增益变化过快。

3.2.2 参考模型

控制系统模型使用二阶系统作为参考模型，如式（8）所示：

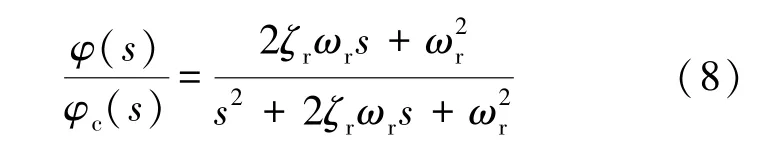
3.2.3 频谱阻尼器

频谱阻尼器输出信号由控制器控制指令输出形成，如式（9）所示：

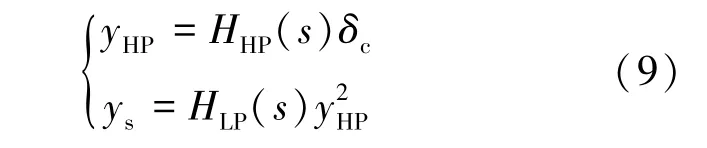
式中，为线性高通滤波器；为线性低通滤波器。 频谱阻尼器结构如图2 所示。

图2 频谱阻尼器结构Fig.2 Structure of spectrum damper

图中高通滤波器和低通滤波器均为线性滤波器，，为滤波器截止频率。

3.2.4 控制架构

AAC 控制回路结构如图3 所示。

图3 AAC 控制回路结构Fig.3 AAC control architecture

4 线性自抗扰容错控制方法

AAC 控制方法仅调节开环回路增益，不改变控制回路结构，对系统容错能力提升有限，本文提出LADRC 方法使用线性扩张状态观测器（Linear Expansion State Observer， LESO）来观测并补偿回路总和扰动，用以有效提升控制器容错能力。

4.1 LESO 时域形式

以俯仰通道为例，其通用模型表达式如式（10）所示：

采用LESO 观测总和扰动项(，，) ，观测器采用式（11）形式：

4.2 LESO 传递函数形式

进一步推导传递函数并化简，得到式（13）：

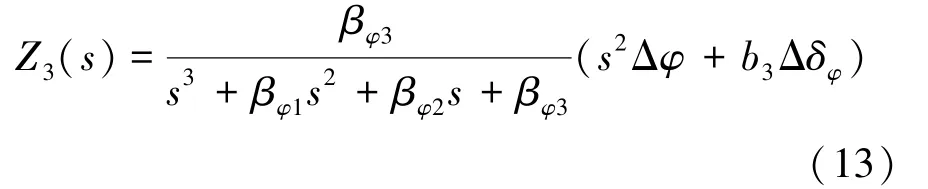
引入控制回路的为两项乘积，相当于滤波提取了第1 项中的部分频带信息，第2 项相当于添加了带滤波的积分项，可以一定程度上消除稳态误差。

为进行频域分析，需推导姿控回路的开环单输入单输出传递函数。 因为LESO 环节为多输入单输出环节，输入量为Δφ（），Δδ（） ，输出量为（），使用摆角指令Δδ（）表示输入量，将系统转换为单输入单输出（Single Input Single Output， SISO）系统，具体形式为式（14）所示：

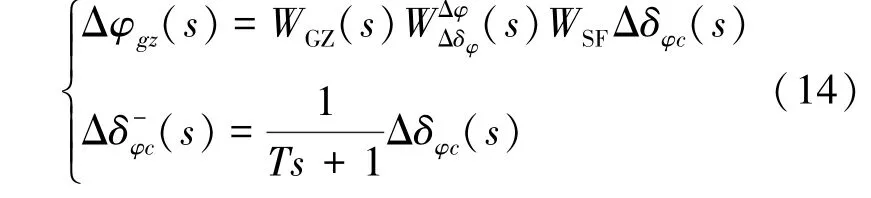
为便于后续推导，将式（14）中部分传函合并，记为式（15）：

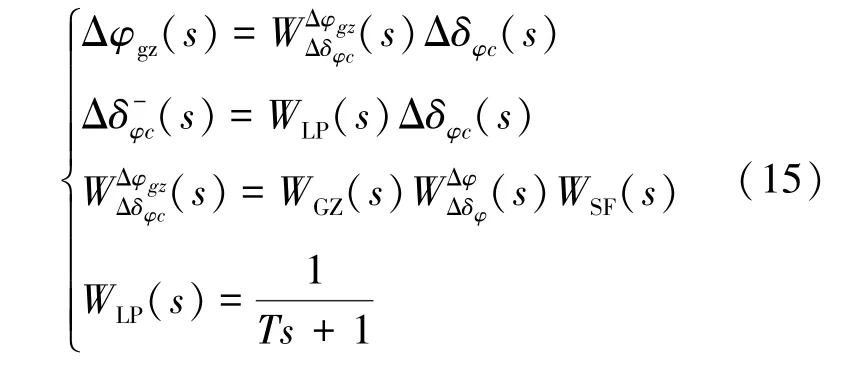
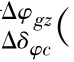
联立式（12）～式（15）可得式（16）：

整理式（16）可得式（17）：

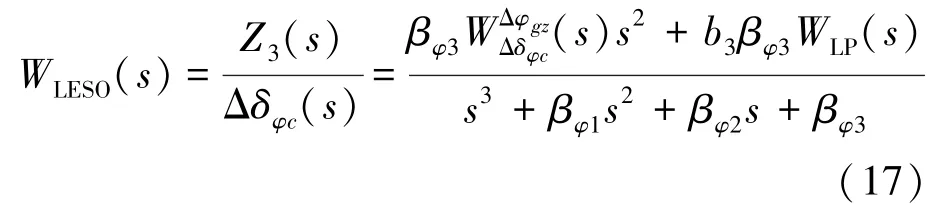
为便于推导，设式（18）成立：

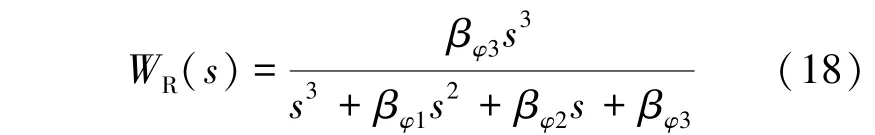
将式（18）代入式（17），可得LESO 环节的单输入单输出形式的传递函数，见式（19）：

4.3 控制器及开环传递函数形式

得到被扩张的状态（）的估计值（），只要已知，控制量就可以得到，如式（20）所示：

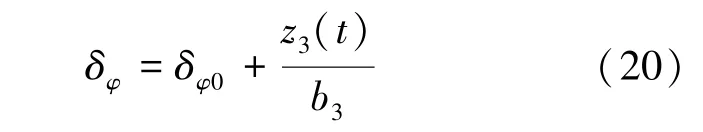
式中，为扩张状态观测器观测得到的总扰动，为动力学中控制力矩系数项，δ为PD 控制器计算控制量。 姿控回路结构如图4 所示。

由图4 可进一步推导形成姿控回路开环传递函数，如式（21）所示：

图4 姿控系统结构图Fig.4 Diagram of attitude control architecture

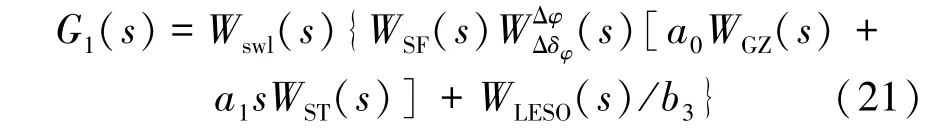
式中，（）为刚性箭体姿控回路开环传递函数，为校正网络环节，为伺服机构环节，为速率陀螺环节，为惯组环节。

将式（17）代入式（21），略去速率陀螺、惯组等测量环节和伺服机构环节，可得式（22）：

4.4 频域分析

本文以俯仰通道为例，基于4.3 节得到的开环传递函数，在频域中分析不同带宽参数对控制系统的影响，结果如表1 和图5 所示。

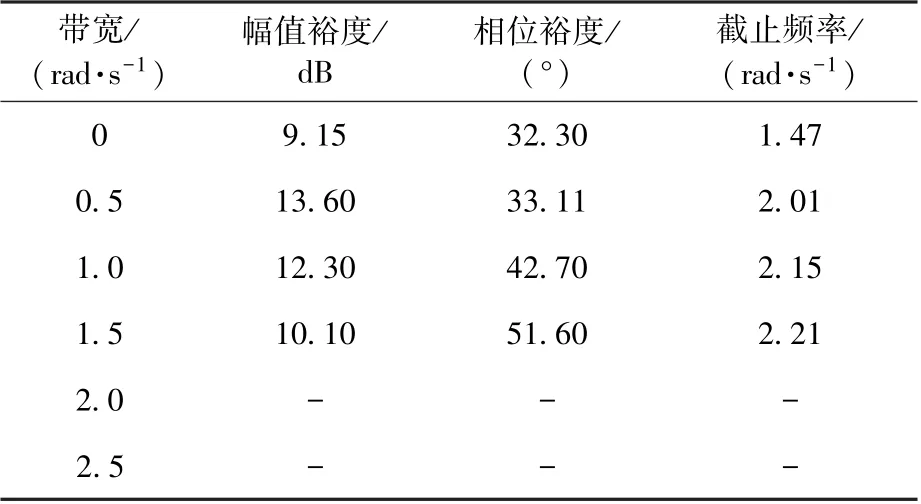
表1 俯仰通道频域指标Table 1 Frequency domain indexes of pitch channel

从表1 和图5 可以看出，LESO 的带宽越大，对相位裕度和截止频率提升的作用就越大，即LESO 环节对控制系统的阻尼和频率均利好，闭环系统的过渡响应主要由截止频率附近的特性所确定，此时越大，其相位裕度提升越明显，系统阻尼比越高。 但是带宽太大，会导致系统的鲁棒性变差，由图5 还可以看出，当＞2 rad／s 时，系统幅频响应曲线会提前穿越0 dB，导致系统的中频区域鲁棒性不好，无法获得纯刚体的幅值裕度与相位裕度，同时幅频曲线整体向上平移，此时需要注意采用相位稳定的低频信号（推进剂晃动和低阶弹性）成分，在0 dB 以上信号的相频曲线是否会穿越（2＋1）π，造成正反馈失稳发散。

图5 不同观测器带宽下的开环姿控系统Bode 图Fig.5 Bode diagram of open⁃loop attitude control system under different observer bandwidths

结合频域分析结果可总结LESO 带宽参数整定规律如下：

1）LESO 的带宽越大，其观测效果越好，对于总和扰动的观测效果就越好；

2）如果被控对象有低频弹性模态或其他低频运动模态，那么LESO 的带宽不应过大，一般要小于被控对象的低频晃动和弹性运动频率，避免将观测到的振动信号引入控制，导致控制－结构耦合问题；

3）LESO 重点观测是刚体运动信号，即测量信号的低频部分。 同时因为测量高频部分信号噪声较大，故LESO 带宽不宜过大。

综上，可明确适应刚晃弹复杂特性约束的液体运载火箭LESO 带宽参数整定准则：高于系统开环截止频率，且低于低阶弹性晃动频率。 本文研究对象一阶弹性模态频率为8 ～12 rad／s，液体晃动频率约为4 rad／s，综合考虑动态性能和稳定性，选取观测器带宽＝1.5 rad／s 开展时域仿真。

5 仿真分析

基于前文所述运载火箭动力学模型，选择助推3 号发动机推力下降典型故障工况，仿真分析LADRC 的故障容错能力，并与PD ＋校正网络、AAC 控制器进行对比。

5.1 参数设置

5.1.1 AAC 控制参数

取相关特征点，确定开环前向增益，使其上下界取值均可保证系统稳定，且裕度满足幅值裕度6 dB， 相位裕度为20°， 故设定∈［0.5，1.5］。

频谱阻尼器截取比一阶弹性频率更高阶的频率信号，故频谱阻尼器的高通滤波器截止频率＝15 rad／s，为取得更好的整形效果，低通滤波器截止频率＝1 rad／s。

控制增益为：＝5e3，＝5e5，＝0.1，＝0.5，＝0.5，＝1.5。

5.1.2 LADRC 控制参数

基于4.4 节分析，综合考虑系统的动态性和稳定性，设置LESO 带宽系数＝1.5 rad／s。

5.2 仿真分析

故障设置为从40 s 开始，助推3 号发动机推力下降100%。 仿真结果如图6～图14 所示。

通过图6～图8 可知，在40 s 植入故障之前，3 种控制器控制效果良好，俯仰、偏航、滚动3 个通道姿态角偏差均较小。 在40 s 植入故障后，俯仰通道PD＋校正网络控制回路作用下的角偏差触发了9°失控门限；AAC 方法可保证系统角偏差小于9°，但整体控制误差较大；LADRC 方法可保证系统稳定且控制误差较小。

图6 俯仰角偏差变化曲线Fig.6 Variation of pitch angle error

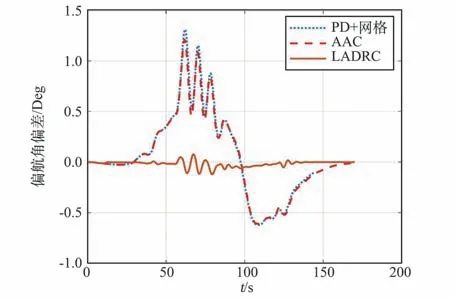
图7 偏航角偏差变化曲线Fig.7 Variation of yaw angle deviation

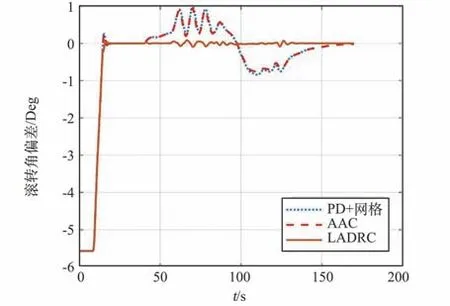
图8 滚转角偏差变化曲线Fig.8 Variation of roll angle deviation

通过图9 ～图11 可知，在故障发生后，AAC因为仅调整了开环控制增益，所以等效控制指令实际上是PD＋校正网络控制指令幅值的缩放，波形没有本质改变。 但是LADRC 通过LESO 有效补偿干扰和故障，其作用相当于带滤波的积分项，使得在故障发生后，控制器快速响应，及时弥补了故障影响。

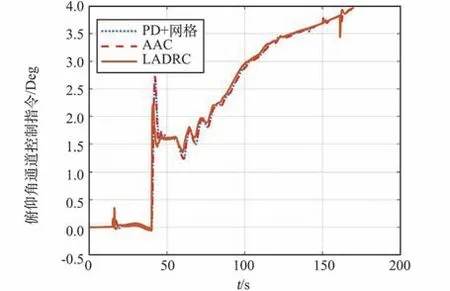
图9 俯仰通道指令对比曲线Fig.9 Comparison of pitch channel commands

图10 偏航通道指令对比曲线Fig.10 Comparison of yaw channel commands

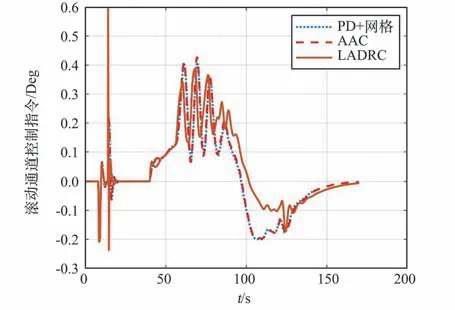
图11 滚转通道指令对比曲线Fig.11 Comparison of roll channel commands

通过图12 ～图14 可知，LADRC 通过LESO观测可有效补偿故障和外部干扰，在客观控制能力允许范围内最大程度挖掘控制能力。

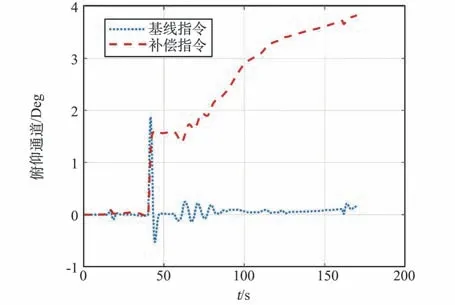
图12 LADRC 俯仰通道指令变化曲线Fig.12 Variation of LADRC pitch channel commands

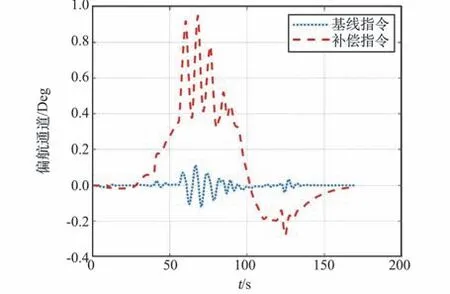
图13 LADRC 偏航通道指令变化曲线Fig.13 Variation of LADRC yaw channel commands

图14 LADRC 滚转通道指令变化曲线Fig.14 Variation of LADRC roll channel commands

6 结论

本文针对液体运载火箭发动机故障情况下的姿态控制问题，提出了线性自抗扰容错姿态控制方法。

1）通过引入惯性环节，推导了包含线性扩张状态观测器的传递函数，解决了扰动观测器环节难以形成传递函数，无法进行频域分析的难题；

2）基于频域分析，针对复杂刚晃弹特性约束液体运载火箭姿控问题，首次提出线性扩张状态观测器带宽参数的整定准则，有效解决了多约束参数难整定的问题。

3）通过时域仿真分析，在给定相同发动机故障工况下，线性自抗扰容错控制方法对故障适应能力明显优于传统控制方法和自适应增广控制。