火灾后型钢混凝土十字形柱的敏感性分析

曲爽， 李威

(山东建筑大学 土木工程学院， 济南 250000)

0 引 言

型钢混凝土异形柱以承载能力高、刚度大、布置灵活、耐火性能好等优点，受到大力推广。然而，在火灾发生后，型钢和混凝土材料性能退化会导致组合柱出现难以预测的失效，该领域的针对性试验很难精确预测组合柱的火灾效应，因此模拟分析是一条便捷之路。在有限元模拟过程中，为与试验的火灾效应更吻合，需要考虑一些建模的重要特征，例如材料的应力-应变关系、热膨胀系数、结构单元的选取等。

唐跃峰等针对方形截面型钢混凝土柱的火灾后性能，建立传热分析模型和结构分析模型，讨论材料强度、受火时间、长细比和含钢率等因素对火灾作用后组合柱剩余承载力的影响，给出剩余承载力简化计算方法。谭清华等建立方形截面型钢混凝土柱的受火全过程有限元模型，分析对比组合柱在常温、火灾后以及加固后承载能力和抗弯刚度的差异。赵框等对方形截面型钢混凝土柱火灾作用后的抗震性能进行有限元模拟，分析轴压比和受火时间等参数对组合柱载荷-位移关系的影响。丁楠等介绍火灾后圆形截面钢管混凝土柱的建模流程，考虑关键参数对组合柱载荷-位移关系及受力性能的影响，其中包括钢管壁厚、加固方式和截面形状等。

关于型钢混凝土组合柱的火灾试验和模拟分析已有大量研究，其主要研究方向是后期的参数分析，而对于型钢混凝土组合柱火灾后的建模特征分析很少。LIU等完成型钢混凝土十字形柱火灾后性能试验与分析。本文采用Abaqus软件建立三维实体有限元模型，对型钢混凝土十字形柱进行参数敏感性分析，以选取最优的建模条件。

1 方案简介

型钢混凝土十字形柱试件的参数设定为：钢骨架采用4根5#型钢与多根直径8 mm的钢筋腹杆连接，计算长度为600 mm，上、下各布置300 mm×300 mm×200 mm的扩大头。

十字形柱的试件参数见表1，偏心载荷布置见图1，热电偶布置见图2。在十字形柱截面布置3个测点记录试件的温度-时间历程，测点1位于腹杆交汇处、测点2位于十字形柱中心、测点3位于型钢外边缘。

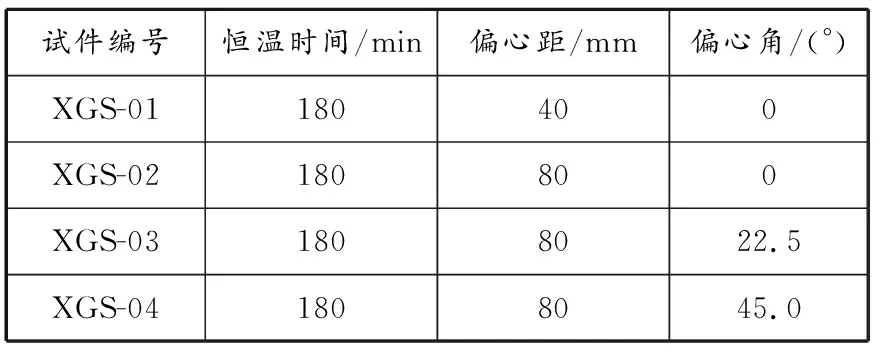
表 1 试件参数

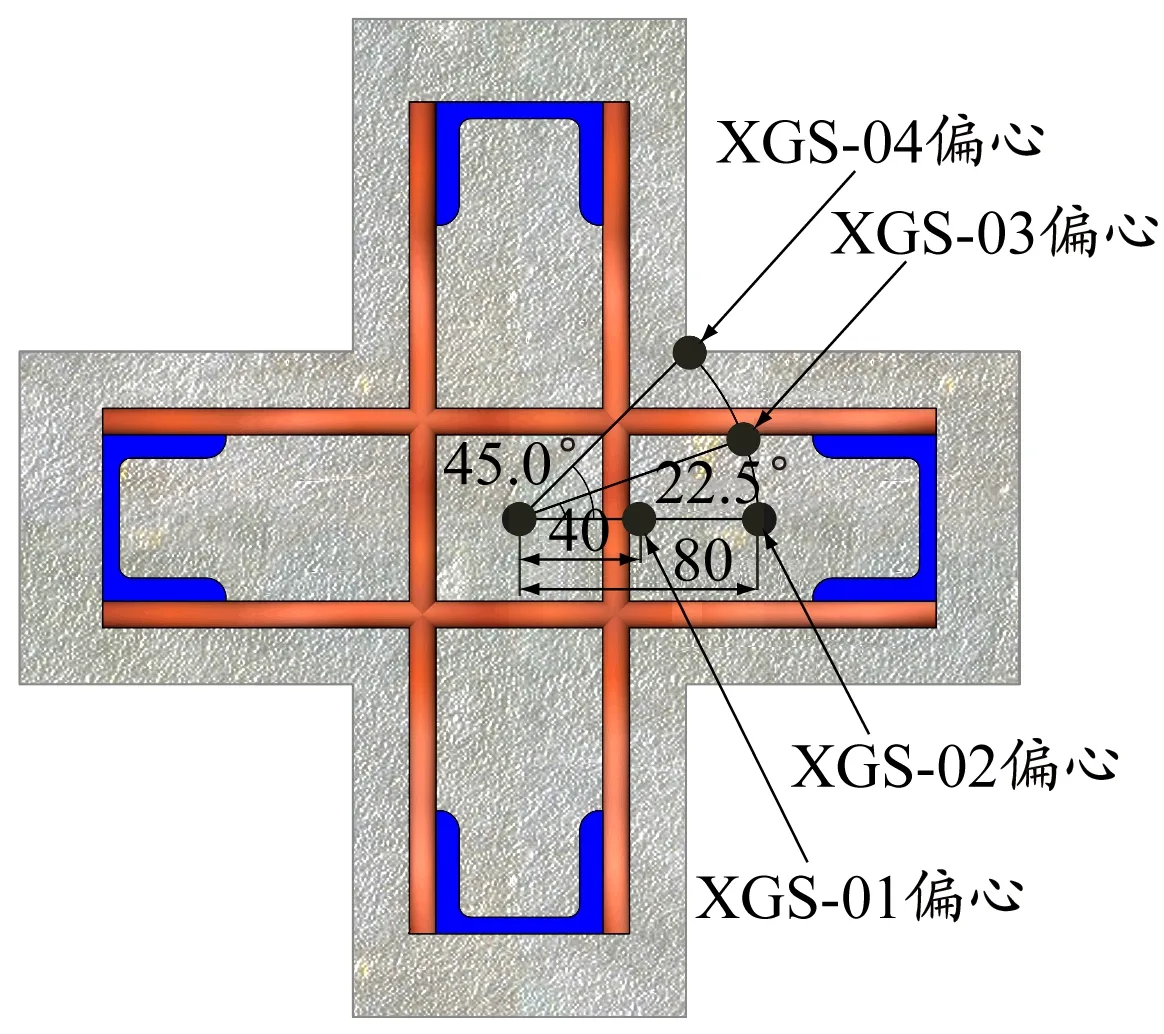
图1 偏心载荷布置

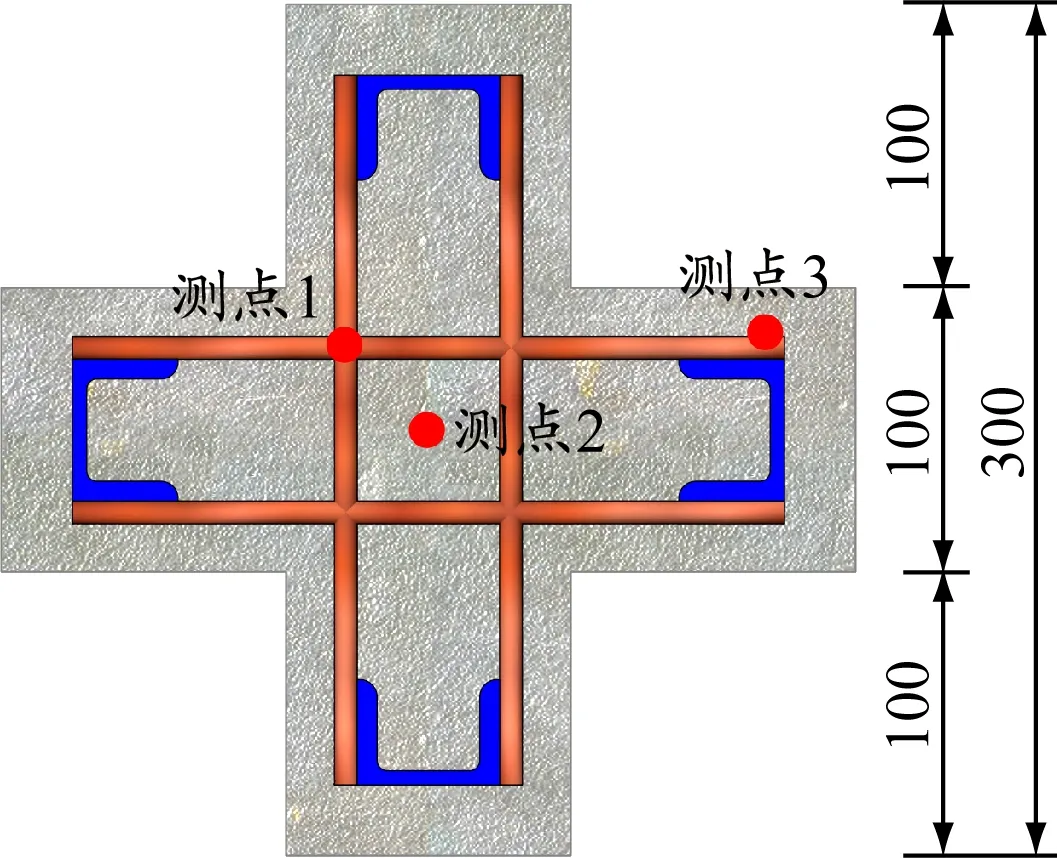
图2 热电偶布置，mm

2 数值模型

2.1 分析方法

进行传热-应力耦合分析通常考虑2种方法：顺序热力耦合方法和完全热力耦合方法。前者需要分别建立传热模型和力学模型，将传热模拟得到的节点温度作为时间函数加入力学模型的预定义场中，从而得到更准确的结果。该方法效率高、易收敛。后者的传热模拟和力学模拟需要在同一模型中运行，且必须同时运算温度场和应力-位移场，计算量大，运行时间长、不易收敛。因此，大部分学者更愿意采用顺序热力耦合的方法进行模拟分析。

2.2 材料特性

钢材和混凝土的热工参数参考欧洲规范提供的数据。高温后钢材和混凝土的本构方程采用陆洲导等的建议，材料属性将在敏感性分析中进一步讨论。

2.3 传热分析

对十字形柱进行非线性传热分析，计算文献[5]试验提供的炉温-时间曲线，通过热对流和热辐射机制进行传热。传热控制参数根据欧洲规范选取：初始环境温度设置为20 ℃，对流换热系数定义为25 W/( m·℃)，热辐射系数定义为0.7，绝对零度定义为-273 ℃，取Stefan-Boltzmann常数= 5.67×10W/(m·K)。

型钢和混凝土采用8节点线性传热六面体单元DC3D8模拟，钢筋采用2节点传热连接单元DC1D2模拟。型钢与混凝土、混凝土与混凝土之间采用Tie约束，网格单元最大尺寸定义为20 mm，十字形柱网格划分结果见图3。温度场模拟结果包含试件所有节点的时间-温度关系，在力学建模时可以将其导入预定义场中。

图3 十字形柱网格划分结果

2.4 结构响应

对十字形柱进行非线性应力分析。为使各个节点的温度能更好地匹配，要保证结构建模的单元网格划分和节点编号与传热模型一致。混凝土采用Abaqus中的混凝土塑性损伤模型定义，导入火灾后的应力-应变关系。混凝土和型钢采用8节点三维实体线性减缩积分单元C3D8R模拟，钢筋采用三维线性桁架单元T3D2模拟。

采用Abaqus中的接触算法定义型钢、钢筋与混凝土之间的相互作用。型钢与混凝土之间采用Tie约束，其中型钢定义为主表面、混凝土的内表面定义为从表面。离散化方法采用表面-表面，忽略型钢与混凝土之间的间隙，以提高计算效率。钢筋与混凝土采用Embedded region约束，其中权系数舍入误差定义为10，外部百分比容差定义为0.05。在顶端轴向载荷作用处和底端混凝土外表面的中心处设置耦合点RP-1和RP-2，用以施加载荷和边界条件。耦合点与混凝土外表面采用Coupling约束，被约束的自由度设为0。在底端耦合点处定义完全固定约束，顶端耦合点处边界条件定义为==0，采用位移载荷的方式进行施压。

在偏心载荷作用下模拟与试验火灾后十字形柱的失效模式对比见图4。模拟云图展示的是外部混凝土的等效塑性应变，模拟结果与实测的破坏情况基本一致。

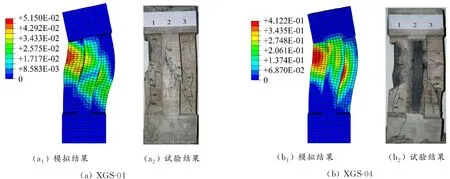
图4 模拟云图与试验结果对比

3 模型验证

3.1 热响应

型钢混凝土十字形柱3个测点的模拟与试验的温度曲线对比见图5。测点1和测点2的升温曲线一致，测点3的升温曲线最接近炉温。十字形柱模拟与试验的升温曲线基本一致。

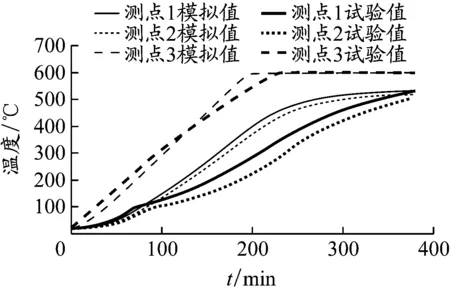
图5 试验与模拟的十字形柱温度曲线对比

3.2 结构响应

在偏心载荷作用下，4个试件剩余承载力模拟结果与实测结果对比见表2，载荷-位移曲线的发展情况见图6。型钢混凝土十字形柱模拟与试验的载荷-位移曲线变化趋势基本一致。十字形柱剩余承载力模拟结果与试验结果比值的平均值和标准偏差分别为1.036和0.03，说明有限元模拟有效。

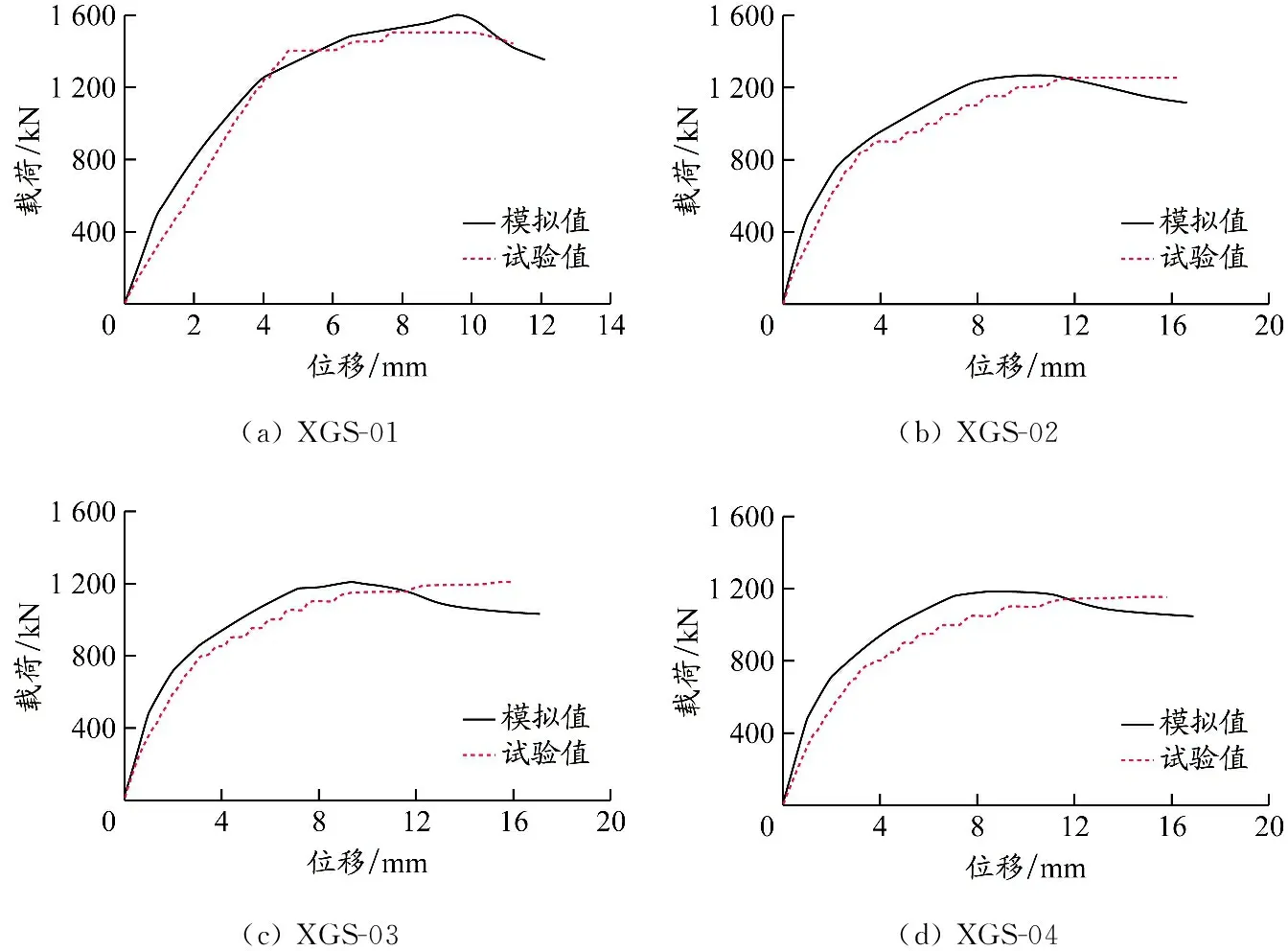
图6 4个型钢混凝土十字形柱试件载荷-位移曲线模拟值与试验值对比

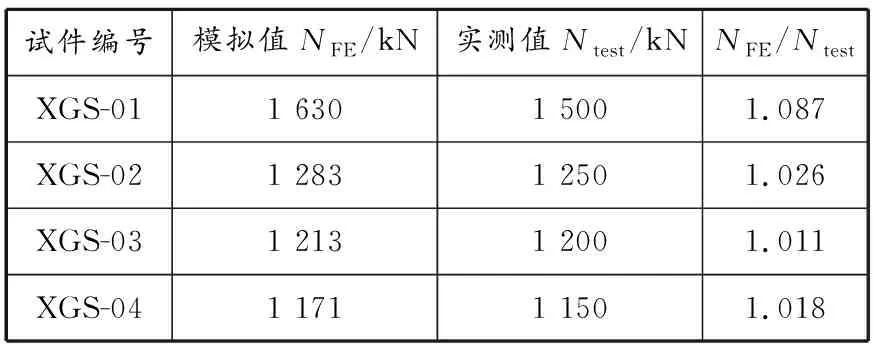
表 2 试件剩余承载力模拟结果与实测结果对比

4 参数敏感性分析

进行参数敏感性分析，研究最佳参数建模方案，选择最佳输入参数值，包括混凝土材料本构模型、单元类型以及热膨胀系数等。

4.1 混凝土本构方程

选取陆洲导等和文献[10]提供的高温后混凝土应力-应变方程进行有限元模拟，并与试验实测的载荷-位移曲线进行对比，结果见图7。陆洲导等提供的本构方程更适合在建模中使用；与实测结果相比，吴波提供的本构方程抵抗行为过大。

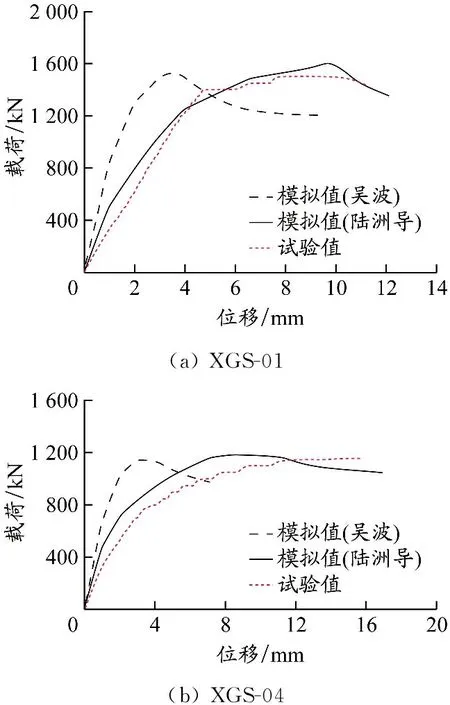
图7 不同混凝土本构关系时模拟与试验载荷-位移曲线对比

4.2 单元类型

混凝土和型钢采用三维实体单元，钢筋采用桁架单元。前者又包括线性C3D8R单元和二次C3D20单元，后者又包括线性T3D2单元和二次T3D3单元。用线性单元与二次单元分别建模并进行计算，结果见图8。不同单元类型的模拟与试验结果基本一致，采取线性单元建模效率更高，且更容易收敛。

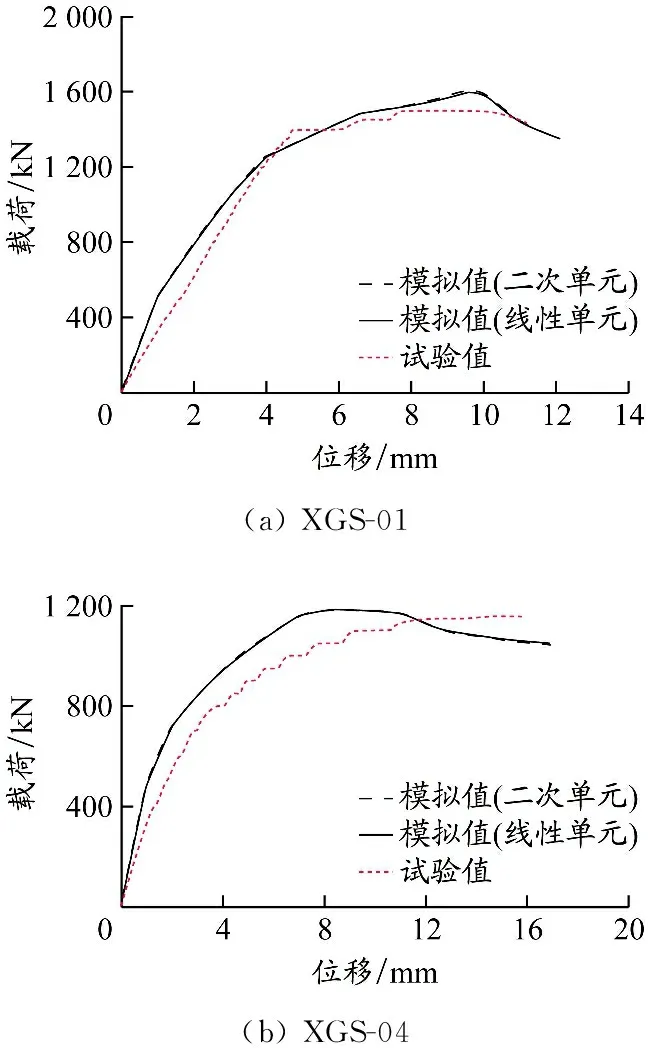
图8 不同单元类型时模拟与试验载荷-位移曲线对比

4.3 热膨胀系数

选取2组热膨胀模型进行对比：第一组取常数，型钢和混凝土的热膨胀系数分别为12×10℃与6×10℃；另一组参考欧洲规范，型钢和混凝土的热膨胀系数设置为与温度相关的参数方程。2组不同热膨胀系数条件下的载荷-位移曲线对比见图9。由此可知，数值模拟对热膨胀系数不敏感，可能是十字形柱核心位置温度过低导致的。

图9 不同热膨胀系数时模拟与试验载荷-位移曲线对比

5 结 论

用有限元法分析型钢混凝土十字形柱的火灾后行为，对建模过程中的参数敏感性进行讨论，得出以下结论。

(1)十字形柱截面温度由外表面到中心逐渐降低，钢筋交汇处温度与截面中心温度升温趋势相似，说明钢筋的传热作用很小。

(2)模拟与试验的破坏模式基本一致。分析火灾后十字形柱的载荷-位移关系，剩余承载力模拟结果与实测结果比值的平均值和标准偏差分别为1.036和0.03，证明有限元模型是有效的，可以为钢-混凝土组合结构的抗火研究提供参考。

(3)参数敏感性分析得到一组最优建模条件：火灾后构件中的混凝土选取陆洲导等提供的应力-应变关系；型钢混凝土结构选用线性单元进行建模；型钢和混凝土的热膨胀系数选用常数表示即可，其取值分别为12×10℃与6×10℃。