外域声场计算中的无限元方法

缪硕， 石敏， 任春雨

(1.华中科技大学 船舶与海洋工程学院，武汉 430074； 2.中国人民解放军 第91977部队，北京 102249)

0 引 言

外域声场问题可以归结为无界域声场的数值求解问题，这类问题的分析不论是在空气中还是在水中都有很多现实需求，如水下航行器的声辐射问题、声散射问题等。

目前，对于声辐射、声散射问题的求解方法主要包括解析法、数值方法。解析法仅适用于较为简单的结构形式，局限性较大；数值方法包括有限元方法、有限元-边界元方法以及有限元-无限元耦合方法等。有限元方法主要进行特殊的边界层处理如设置PML等，但计算频率越高、模型越大，其边界层网格数就越多，影响计算效率。有限元-边界元方法的方程求解存在奇异性、多值解等问题，影响其在实际工程中的应用。有限元-无限元耦合方法将无限域分为内部域和外部域，内部域采用有限元离散，在边界处采用无限元单元求解外场声学问题，带来的额外的计算自由度较少，适用范围广。

对于有限元-无限元方法，国内外已经有相当多的研究。ASTLEY等在BURNETT等无限元思想基础上提出一种新的无限元单元类型，其将形函数的共轭作为伽辽金加权残值法的权函数，消除方程中的不确定积分，简化求解方程。ASTLEY等进一步改善其数学严谨性以及适用性，发展成为映射包络元亦即Astley元，并求解偶极子、四极子等的声场特性。CREMERS等将Astley元进一步发展成可实现任意变阶的波包络单元。杨瑞梁等阐述无限元的发展现状，并对无限元进行归纳分析，细致地给出各方法的原理及问题，并展望无限元的发展前景。庞福振利用无限元方法预报船舶的结构噪声，发现相对于无反射边界条件，无限元方法精度更高，而且对于远场声辐射求解方便、计算效率高。尹旭超提出一种可任意变阶的声学无限元，并基于MATLAB计算单极子等声辐射以及柱壳声散射问题。苏楠等和田正东等都验证无限元方法求解声学问题的准确性，并利用无限元方法研究层圆柱壳层厚度、内部结构等对于圆柱壳的均方振速及辐射声功率的影响。JIANG等采用有限元-无限元方法分析滚筒洗衣机的低频噪声，并将计算结果与实验方法测量的辐射噪声进行对比，发现计算结果与实验结果吻合较好。MOHEIT等为避免在低频计算时需要构建较大的完美匹配层(PML)，通过算例验证无限元的有效性，并利用其开展声子晶体在自由声场中特性的分析；同时利用有限元-无限元耦合方法探究有限元单元大小及无限元单元在无穷远方向上的插值多项式及插值节点数对外场声学模态的影响。吴健等讨论采用网格由细到粗的过渡划分策略对计算结果的影响，验证合理划分网格有利于计算。目前，有限元-无限元耦合方法以声辐射特性的研究为主，研究对象包括柱壳、锥壳、船体结构等，但关于声散射特性以及有限元-无限元方法计算结果影响要素的研究较少。

本文以脉动球源和刚性小球为对象，研究单元类型及单元大小等对声学问题计算结果的影响，为工程中的声学计算提供参考。

1 计算方法

有限元-无限元耦合方法可以在结构表面施加载荷，模拟流-固耦合作用并利用无限元单元求解外场的声辐射特性；也可以设置入射声波，模拟声波与结构的相互作用，并利用无限元单元求解外场的声散射特性。有限元-无限元耦合方法利用人工截断边界将无限大求解域分为内部域和外部无限大域，如图1所示，内部域包含流体域和结构域，结构域内部可以包括复杂内部结构，内部域采用有限元单元离散；外部无限大域采用无限元单元离散，并在截断边界处设置无限元单元，以消除边界影响并求解外声场。

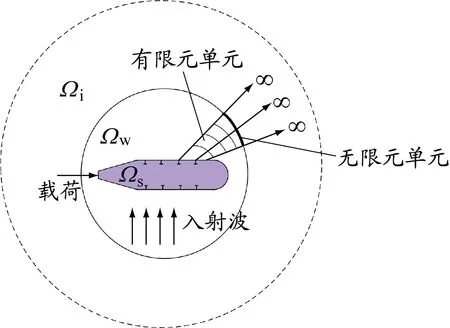
图 1 有限元-无限元耦合方法原理示意

1.1 有限元-无限元耦合方法

对于理想声学介质，声波在其中的传播需要满足Helmholtz方程

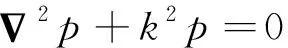
(1)

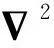
对于有限元离散流场，其离散域必定有边界的存在，当声波在其内传播时，边界阻抗的不匹配会导致声波在边界处产生反射。在有限元边界处设置声学无限元，可以消除边界影响，模拟无限大流域，因此有限元-无限元耦合方法需要在边界处满足阻抗匹配边界条件：

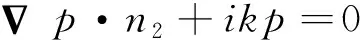
(2)

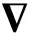
设结构域表面的加速度大小为，则在结构-声学边界处为保证其连续性，声场和结构应当满足：

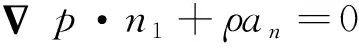
(3)

式中：为流场密度；为声结构边界法向。

应用Galerkin加权残值法对声场进行求解，首先设声压的近似解

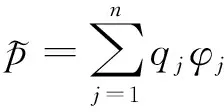
(4)

式中：为基函数或形函数(以下统一称为形函数)；为待定系数，=1,2,…,。

对Helmholtz方程、声结构表面处边界及截断处边界取场函数及边界条件的加权积分，有

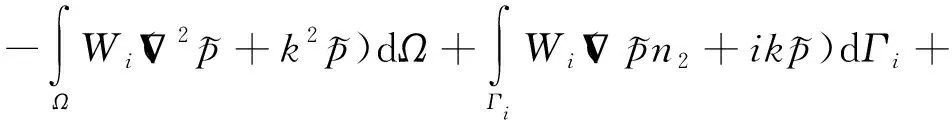
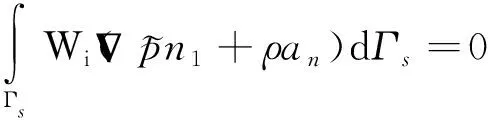
(5)

式中：为伽辽金方法权函数，=1,2,…,。

将声压近似解表达式写成形函数与待定系数的乘积，则式(5)可表示为

(+ik-)=

(6)

式中：为待定系数矩阵，其各元素为近似解表达式中的待定系数；为刚度矩阵；为阻尼矩阵；为质量矩阵；为声学载荷矩阵。

刚度矩阵、阻尼矩阵、质量矩阵、声学载荷矩阵的元素表达式为

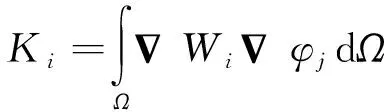
(7)

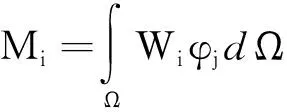
(8)

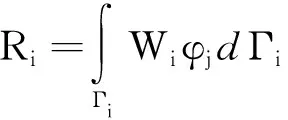
(9)

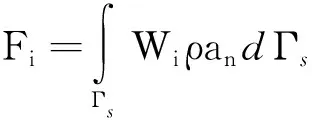
(10)

由式(7)～(10)可知，当选取权函数为形函数的共轭时，可以使得求解过程得到极大的简化，以下着重讨论形函数的选取。

2.2 单元的形函数

以二维典型单元为例，说明有限元及无限元单元形函数的形式，以及2种单元在相交边界处的关系。在内部域采用有限元进行离散，在局部坐标系-下形函数的表达式为

(,)=(,)

(11)

为表述方便，选取4节点矩形单元，单元及各点坐标见图2，各节点形函数的表达式见式(12)～(15)，对应图形见图3。

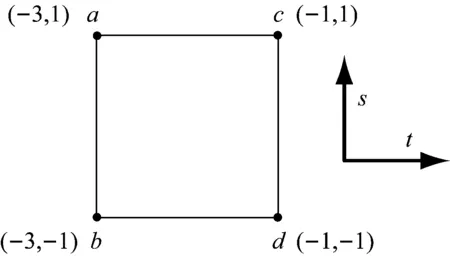
图 2 局部坐标系4节点矩形单元示意

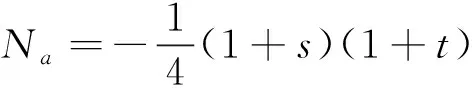
(12)

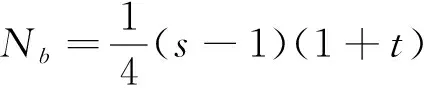
(13)

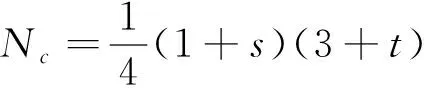
(14)

(15)

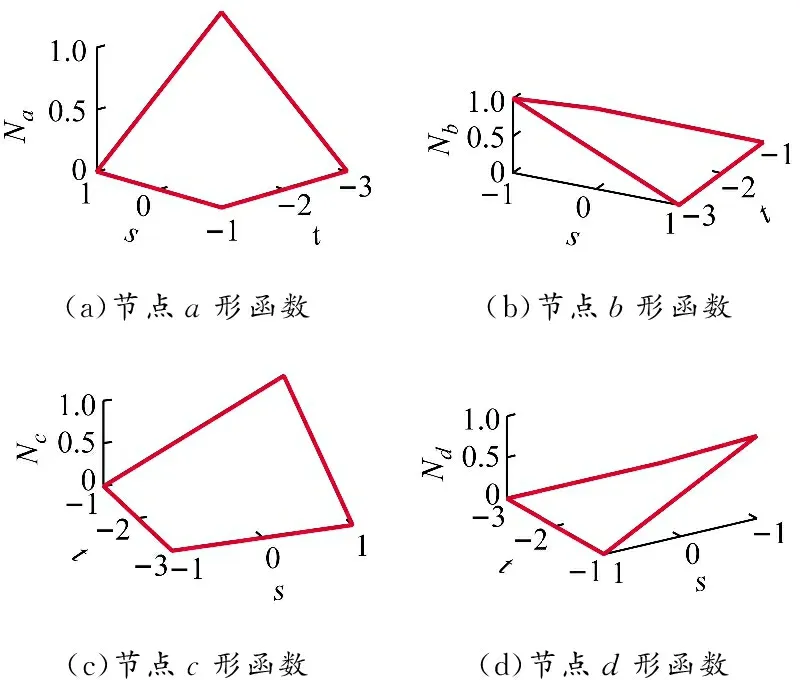
图 3 4节点矩形单元各节点形函数

图4为无限元单元示意，其中，图4(a)为局部坐标系-下的无限元单元，图4(b)为全局坐标系-下的无限元单元，1、2为人工截断边界上的节点，2个坐标系下无限元各节点相对应。2种坐标系之间的映射函数见文献[9]，通过坐标变换使得全局坐标系中无穷远处对应局部坐标系中=1。

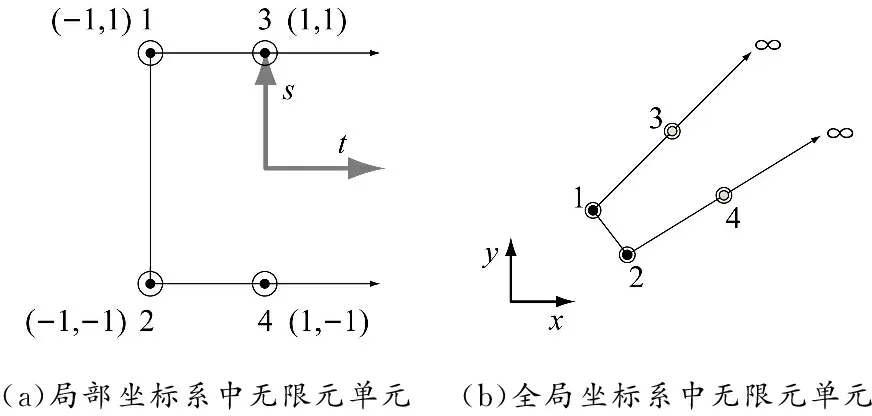
图 4 声学无限元单元

无限元单元的形函数(,)可以表示为

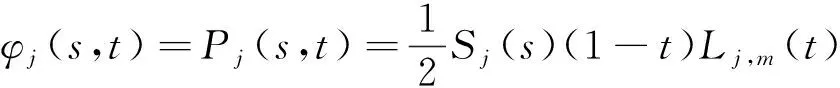
(16)

式中：

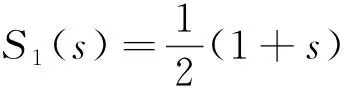
(17)

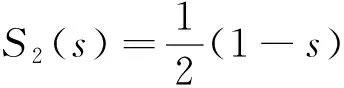
(18)

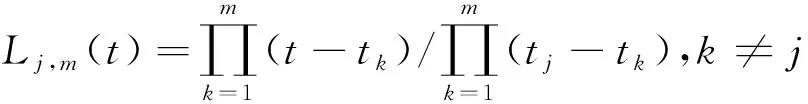
(19)

()为无限元单元为沿局部坐标系轴的形函数，,为沿局部坐标系轴方向上的拉格朗日多项式，为局部坐标系轴方向上的节点数。

在给出的2种形函数基础上，进一步讨论单元形函数在边界处的情况。图5为坐标交换后的有限元单元和无限元单元，有限元单元在边界处节点1、2的形函数为式(16)，无限元单元的形函数为式(20)～(21)。

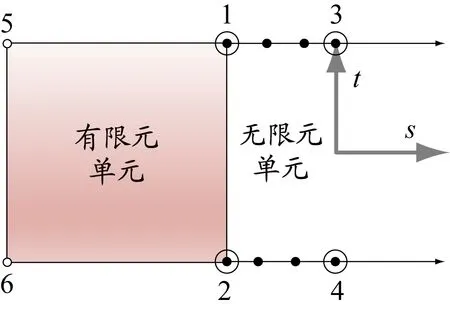
图 5 坐标变换后有限元单元和无限元单元

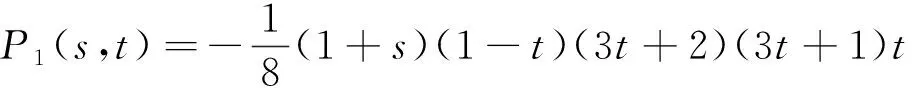
(20)

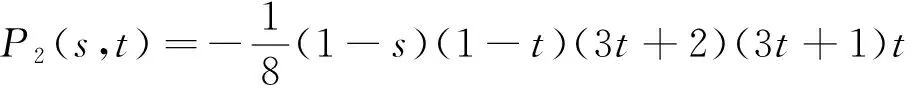
(21)

将无限元域和有限元域二者形函数绘制在一起，如图6所示。当<-1时代表有限元单元的形函数，-1<<0时为无限元单元的形函数，二者在边界处=-1时能够保持连续。

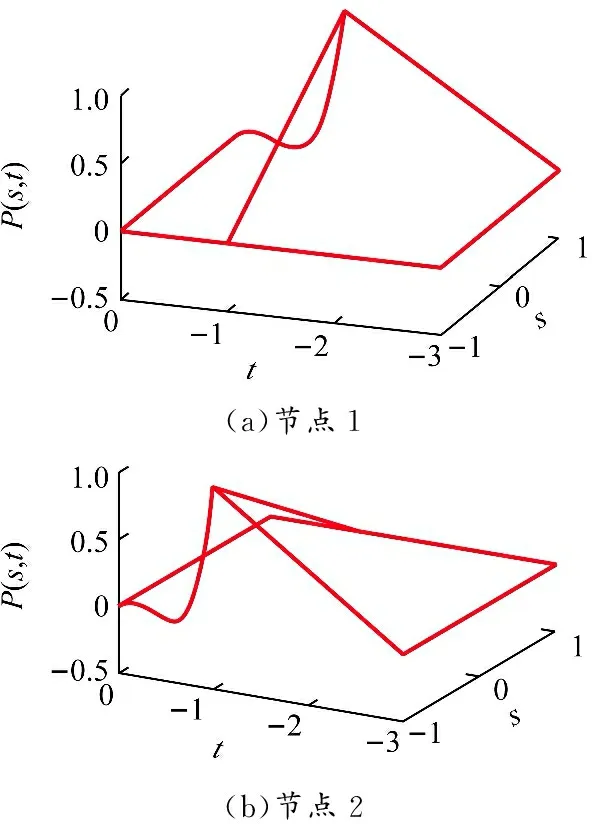
图 6 有限元、无限元形函数

3 计算方法影响要素

在实际的外域声场计算中，由于模型规模大以及计算频段宽等原因，计算量巨大，往往无法达到精确解的计算要求，有必要讨论多种要素对于计算结果的影响。本文选取单元类型、单元大小这2种影响要素，从声辐射、声散射2个方面进行分析。

3.1 声辐射问题精度

声辐射问题的研究对象为某脉动球源，半径0.1 m，其外部为半径0.2 m的球形水域，见图7所示，在水域表面上设置无限元单元。本次的计算频率为10 kHz，在计算软件Abaqus中，在球源表面施加声压边界条件=1 Pa。流体密度为1 000 kg/m，声速为1 440 m/s，文中水域材料参数均保持一致。

图 7 声辐射问题示意及模型

通过改变单元类型、单元大小探究其对辐射声场计算结果的影响。单元大小为0.03和0.02 m时，三角形和四边形单元(均包含一次单元和二次单元)的脉动球源网格模型见图8，一次单元与二次单元的网格相同。

图 8 不同单元类型及单元大小的脉动球源网格示意

一次和二次单元网格数相同，为比较二者对计算结果的影响，以节点数代表单元大小。本次计算结果以2种形式给出，以便对比单元类型和大小对辐射声场声压计算结果的影响。

第一种形式：

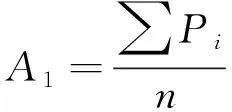
(22)

式中：代表有限元水域外表面上第个点的声压;为节点总数。代表水域外表面所有节点声压均值大小。

第二种形式：

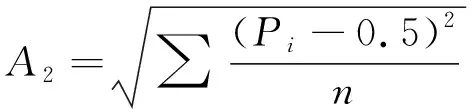
(23)

式中：0.5代表水域表面声压大小理论解。表示水域外表面所有节点声压的误差均方值。

2种形式的计算结果见图9。由此可知，随着节点数的增多，4种单元均可以较好地求解水域表面的辐射声场。为进一步分析，以5%的误差为标准列出各网格类型下、满足精度要求对应的节点数及单元大小，结果见表1。

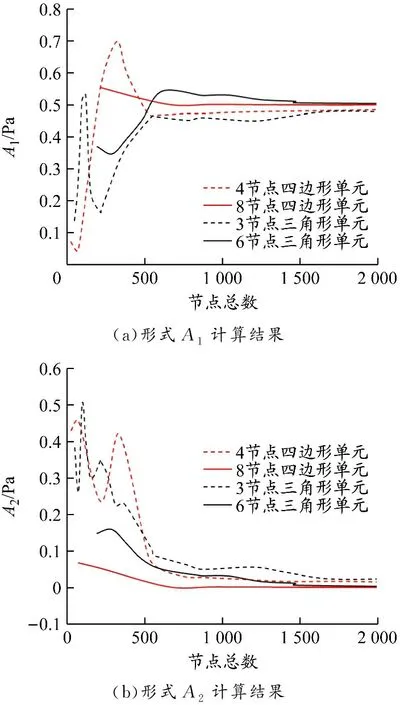
图 9 不同单元类型及节点总数下辐射声压无限元计算结果

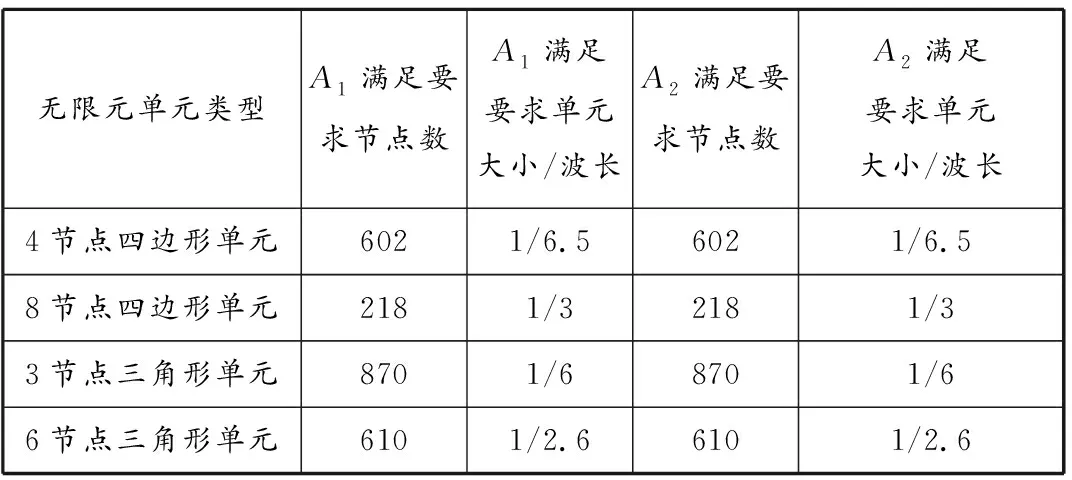
表 1 声辐射问题满足精度对应的节点数及单元大小

由表1可知，为满足精度要求，4节点四边形单元、3节点三角形单元的单元大小需要达到计算频率对应声波波长的1/6，8节点四边形单元、6节点三角形单元的单元大小仅需为对应声波波长的1/3及1/2.6，其原因是二次单元的插值形函数阶数较高，可以较好地实现对声场的模拟。

此外，和结果达到精度要求时，对应的节点数及单元大小基本一致，只需选择其中一种进行计算即可。

3.2 声散射问题精度

声散射问题选取刚性小球为对象，小球半径大小、水域大小、网格划分与声辐射问题中处理一致。计算频率为1～10 kHz，在Abaqus中设置入射波形式为平面波，声压大小为1 Pa。

为便于后续对比分析，选取刚体表面上一点的声压，探究单元类型、单元大小对计算结果的影响。不同单元类型及大小下的模型示意图与第3.1节中图8类似，此处不再赘述。5 kHz下基于有限元-无限元耦合方法的声压计算结果见图10。

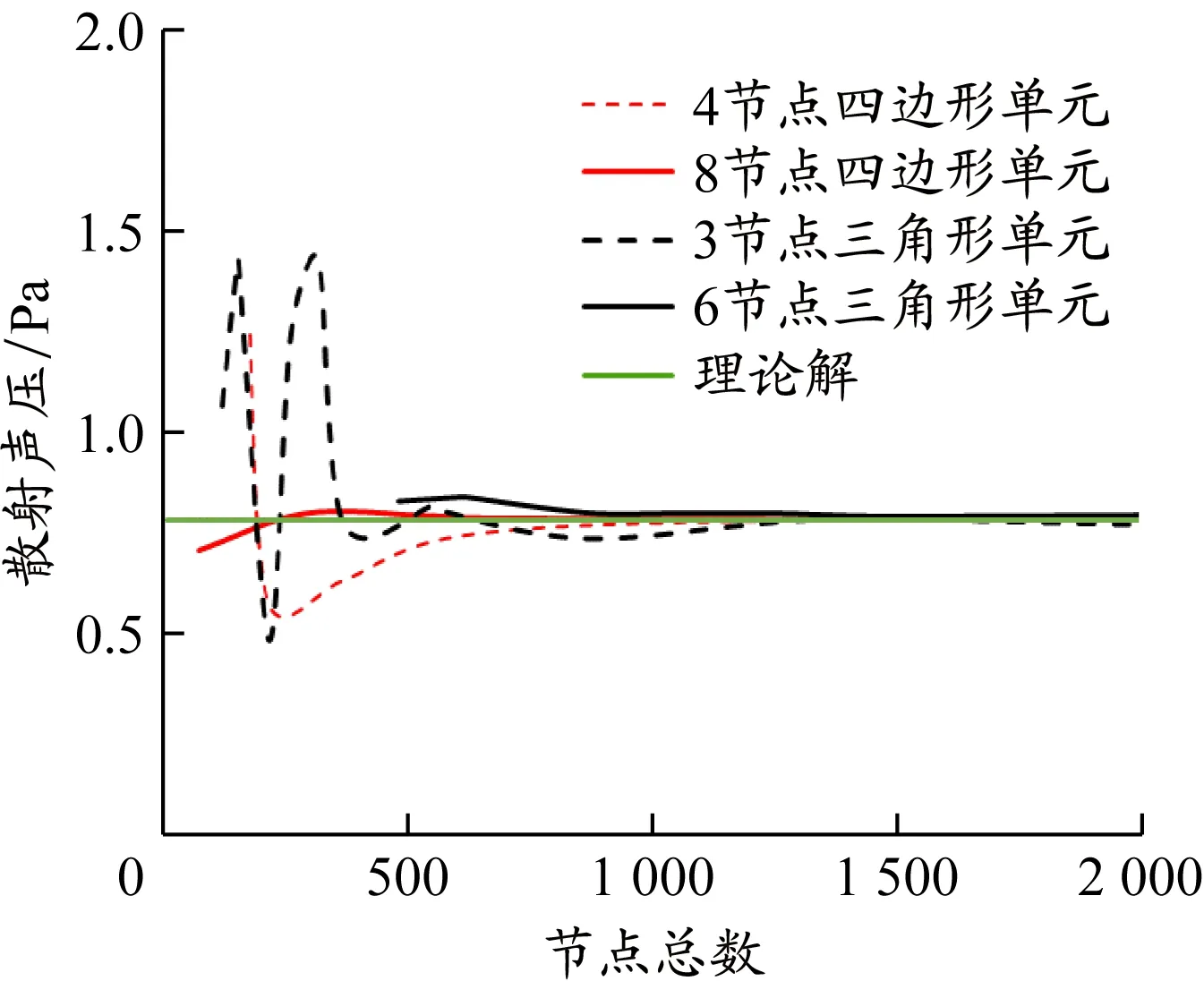
图 10 5 kHz下不同单元类型、大小散射声压无限元计算结果

由图10可知，当4种单元类型达到一定数量时，均可以较好地求解散射声场。为进一步分析其收敛特性，以5%误差为标准列出满足精度要求的节点数以及对应单元大小，结果见表2。

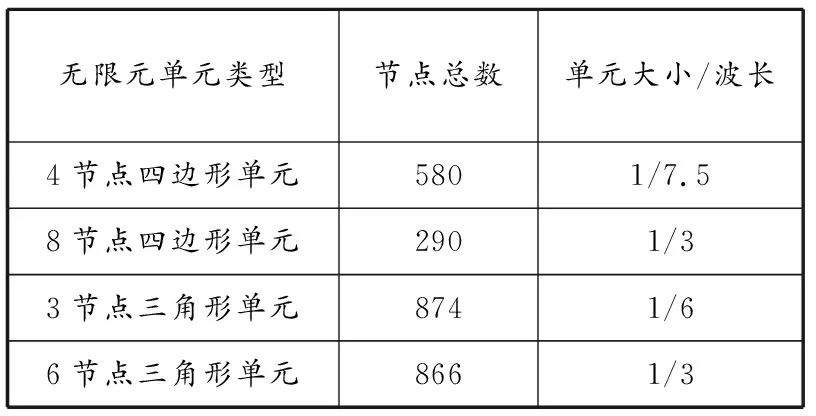
表 2 5 kHz下声散射问题满足精度对应的节点总数及单元大小

由表2可知，为满足误差要求，在5 kHz时4节点四边形单元、3节点三角形单元的单元大小需要达到计算频率对应声波波长的1/7.5及1/6；而对于8节点四边形单元、6节点三角形单元的单元大小仅需约为对应声波波长的1/3，声散射相比声辐射对网格的要求稍高。

4 结 论

基于有限元软件Abaqus，采用有限元-无限元耦合的方法开展声辐射、声散射计算问题的研究，讨论该方法中单元类型及单元尺寸等对声场计算求解的影响，通过仿真结果发现：

(1)有限元-无限元耦合方法适用于声辐射、声散射问题的计算分析，且计算结果满足精度要求。

(2)二次单元的单元大小仅需为求解频率对应波长的1/3左右，计算结果即可满足一定精度要求。总之，通过构建二次单元可以提高计算效率。

需要说明的是，本文虽然仅讨论无限元方法在外域声场计算中的应用，但该方法同样适用于内域问题。另外，本文的计算方法可应用于工程结构(如舰船与潜艇)的外域声场计算，虽然许多工作还有待深入，如无限元外部形状对计算的影响，以及考虑结构的材料属性时的结构与流体耦合问题等，这些问题都将在后续的工作中进行讨论。