型钢活性粉末混凝土柱偏心受压性能有限元分析

2022-06-29周绍朋

计算机辅助工程 2022年2期

周绍朋

(山东建筑大学土木工程学院，济南 250101)

0 引言

随着经济技术的快速发展，高层、超高层以及大跨度建筑在实际工程中不断涌现，对建筑材料的力学性能提出更高的要求。活性粉末混凝土(reactive powder concrete, RPC)具有高韧性、高耐久性、高抗压抗折强度等优点，型钢RPC组合结构可充分发挥钢材和RPC各自的优势，在现代化建筑结构中有着良好的应用前景。

何叶等利用有限元软件Abaqus对不同配箍率和含钢率的型钢混凝土柱复合受力下的抗扭性能进行数值模拟，结果表明提高配箍率和含钢率可以提高型钢混凝土柱的承载力。王震强考虑配筋率、混凝土强度和含钢率的影响，对型钢混凝土柱的承载性能进行有限元模拟分析，结果表明提高含钢率能够有效提高试件的承载能力，提高配筋率和混凝土强度能增强试件的延性。郑山锁等采用Ansys对不同偏心率和长细比的型钢混凝土偏压柱进行数值分析，模拟结果与试验结果吻合较好。

在型钢RPC组合结构方面，学者们也展开一系列研究。卜良桃等对6根型钢外包RPC柱进行轴压和偏压试验，并进行有限元分析，模拟结果与试验结果吻合度较高。卜良桃等对3根不同RPC强度的型钢外包RPC柱进行偏压试验，结果表明偏心距为60 mm时出现大偏压破坏形态，且RPC强度越高，试件承载力和刚度越大。卜良桃等考虑偏心距和含钢率的影响，对6根型钢RPC柱进行大偏压试验，结果表明试件极限承载力随含钢率提高而增大，随偏心距增大而降低。SHI等设计22根钢筋RPC柱并对其进行大偏压试验，考虑RPC配筋率和有无钢纤维的影响，结果表明RPC强度越高，试件承载力越高，且推导出钢筋RPC柱在大偏心受压时的极限载荷计算方法。刘畅考虑不同偏心率的影响，对无筋RPC短柱进行试验，得到此类构件在不同偏心率时的极限载荷。黎红兵等对3根不同强度的型钢RPC柱进行轴压试验，结果表明试件的极限承载力随RPC等级提高而增大。

以上一系列试验研究为型钢RPC柱的力学性能提供一定的理论基础，但是对于不同偏心形式下的型钢RPC偏压柱承载性能的试验研究和模拟分析相对较少。本文设计6个型钢RPC柱进行偏心受压试验，考虑不同偏心距和加载角的影响。利用有限元软件Abaqus进行模拟分析，对比不同试件极限载荷和载荷-位移曲线的变化规律，探究偏心距和加载角对型钢RPC偏压柱承载性能的影响。

1 试件模型及概况

1.1 试件设计

参考《混凝土结构设计规范》《组合结构设计规范》和《活性粉末混凝土》等规范，考虑不同偏心距和不同加载角对型钢RPC偏压柱承载性能的影响，共设计6根RPC试件，试件详细参数见图1。使用TM800B压力试验机采集系统采集试验过程的竖向压力和竖向位移，采用三级加载方法，加载装置见图2。

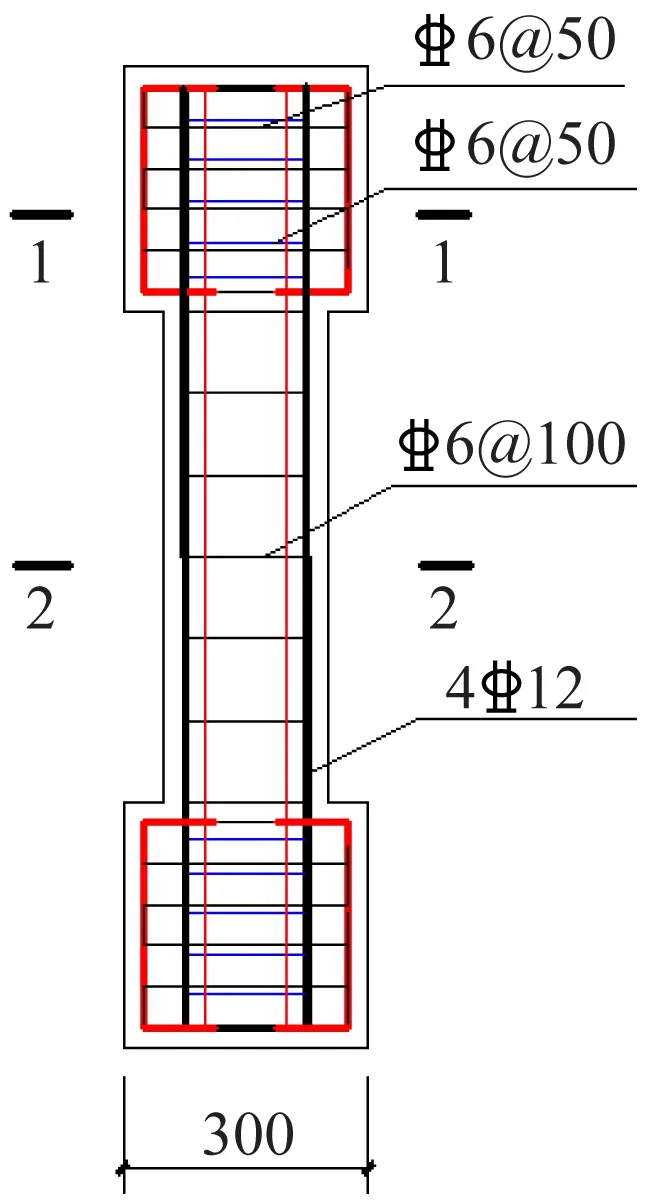
图 1 试件尺寸及配筋,mm

图 2 加载装置示意

1.2 材料参数

试件纵筋和箍筋采用HRB400钢,纵筋直径12 mm,箍筋直径6 mm，配置H型钢为Q235钢，尺寸为100 mm×100 mm×6 mm×8 mm。型钢和钢筋的力学性能按《金属材料室温拉伸试验》的要求进行测试，结果见表1。根据《普通混凝土力学性能试验方法标准》,制作6个100 mm×100 mm×100 mm的RPC立方体试块进行抗压试验，测得RPC的平均抗压强度为114.3 MPa，平均弹性模量为40.8 GPa,各试块测试结果见表2。

表 1 钢材的力学性能参数 MPa

表 2 RPC试块的抗压试验结果

2 数值模拟

2.1 模型参数

采用有限元软件Abaqus对型钢RPC柱建立有限元模型，分析不同偏心距和不同加载角对型钢RPC柱承载性能的影响。

表 3 试件设计模型参数

2.2 模型建立

在有限元模拟中，RPC采用塑性损伤模型和郑文忠等提出的本构模型。模型中的钢材采用理想弹塑性模型，钢材的本构关系曲线见图3，其应力-应变关系为

图 3 钢材本构关系曲线

(1)

式中：为钢材的弹性模量；为钢材的屈服应变。

RPC采用8节点线性六面体单元C3D8R，RPC有限元模型见图4。型钢选用三维实体单元C3D8R，型钢有限元模型见图5。钢筋和箍筋选用桁架单元T3D2，钢筋骨架使用嵌入式区域内置于混凝土中，钢筋骨架有限元模型见图6。

图 4 RPC有限元模型

图 5 型钢有限元模型

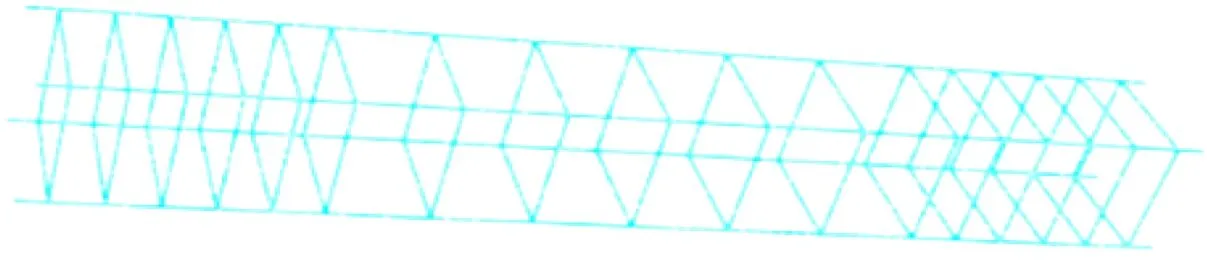
图 6 钢筋骨架有限元模型

3 模型验证

对型钢RPC试件的承载性能进行有限元模拟，其极限载荷和极限位移的试验结果与模拟结果对比见表4。模拟结果与试验结果存在一定误差但误差较小，可认为该模拟结果与试验结果基本一致。

表 4 RPC试件极限载荷和极限位移试验结果与模拟结果对比

各个试件载荷-位移曲线试验结果与模拟结果对比见图7。可以看出，试验曲线与模拟曲线的走势和极限载荷均几乎相同。在模拟结果中，RPC和钢材强度均在理想状态下得到充分发挥，试件破坏时产生的位移略大于试验结果，可认为所建立的模型可用于分析型钢RPC偏压柱的承载性能。

图 7 各试件载荷-位移曲线试验结果与模拟结果对比

4 模拟结果及分析

4.1 极限载荷分析

4.1.1 不同偏心距时试件的极限载荷

对不同偏心距的试件1～4进行模拟，其极限载荷值依次为4 988、3 115、2 992和2 160 kN。试件1～4的极限载荷逐渐减小，与试件1相比，试件2、3、4的极限载荷分别减小37.6%、40.0%和56.7%。这表明型钢RPC柱的承载力随着偏心距的增大而减小，偏心距对极限承载力的影响较大。

4.1.2 不同加载角时试件的极限载荷

对试件4～6进行不同加载角模拟，其极限载荷值依次为2 160、2 090和2 012 kN。与试件4相比，试件5和6的极限载荷分别下降3.2%和6.9%。这表明当偏心距一定时，极限载荷随加载角的增加而降低，但加载角对试件承载力的影响相对较小。

4.2 载荷-位移曲线

不同偏心距和不同加载角试件的载荷-位移曲线见图8和9。在加载前期,偏心受压试件的载荷-位移曲线基本为线性，表明该阶段试件为弹性变形阶段，该阶段曲线的斜率可以反映试件的刚度大小。随着载荷的增大，曲线斜率开始下降，纵向位移增长加快，试件内部开始出现裂缝，此阶段受拉侧型钢翼缘参与受力，承担受拉侧的拉应力。当加载至极限载荷时，曲线均出现突降，随着纵向位移的增大，载荷下降，表现为延性较好。