基于麻雀算法的MCR-WPT系统传输特性研究*

常雨芳， 唐 杨， 李 飞， 阎 晟， 尹帅帅， 黄文聪

(湖北工业大学 电气与电子工程学院,湖北 武汉 430068)

0 引 言

磁耦合谐振式无线电能传输(magnetically-coupled resonant wireless power transmission,MCR-WPT)通过具有相同谐振频率的磁耦合机构近场耦合实现电能的无线传输。

目前，MCR-WPT研究的重点是传输功率、传输效率、传输距离[1～3]。文献[4]通过改变线圈的形状、线圈参数提高了系统的传输性能，但没有研究负载对电能传输系统的影响。文献[5]通过DC/DC变换器改变系统的等效负载使系统输出功率最大，但没有研究等效负载对传输效率的影响。文献[6]通过DC/DC变换器改变系统的等效负载和锁相环调谐使系统的传输效率最高，但没有研究等效负载和频率对输出功率的影响。文献[7]通过单发射线圈—双谐振并联接收线圈结构提高了传输效率、传输距离，但没有研究该结构对输出功率的影响。文献[8]通过差分进化算法提高了四线圈电能传输系统的传输效率、传输距离，但该系统的互感线圈发生纵向抗偏移时系统传输效率骤降。文献[9]通过遗传算法对互补对称式LCC型谐振网络的WPT系统参数进行优化，提高了系统传输效率，但遗传算法的局部搜索能力较弱，容易过早地收敛。文献[10]通过改进粒子群算法对WPT系统的频率进行跟踪，提高了系统的输出功率，但最大功率点的谐振频率过大，对人体健康存在安全隐患。

本文在上述研究的基础上，以提高MCR-WPT系统的传输效率为目标，通过改进麻雀搜索算法(chaotic sparrow search algorithm,chaotic SSA)对影响系统传输效率的多个参数的匹配问题进行优化，找到最大传输效率对应的最优参数匹配值，使得MCR-WPT系统工作呈最佳传输效率状态。

1 MCR-WPT系统理论研究

传统两线圈MCR-WPT系统的电路拓扑结构主要有以下4种：串联—串联型补偿电路、串联—并联型补偿电路、并联—串联型补偿电路、并联—并联型补偿电路。在一定条件下，串联—串联补偿电路具有抗偏移性能强、输出电流恒定的特点，故本文采用串联—串联补偿电路对电能传输系统进行建模分析，MCR-WPT系统等效电路模型如图1所示。

由图1可知,发射端的等效阻抗为Z1=RS+R1+jωL1+1/jωC1；接收端的等效阻抗为Z2=R2+RL+jωL2+1/jωC2。

由基尔霍夫电压定律，可确定每个谐振回路电流，如下式所示

(1)

式中ω为角频率，M为线圈互感。

根据上述公式，可以得到两回路电流

(2)

当系统处在谐振状态时，此时的谐振角频率为

(3)

输入功率Pi为

(4)

输出功率Po为

(5)

传输效率η为

(6)

式中Z=(R1+RS)(RL+R2)。

由式(5)和式(6)可知，MCR-WPT系统的输出功率和传输效率均与电源角频率ω,互感系数M,负载电阻RL,两回路的等效电阻R1和R2以及电源内阻RS等参数密切相关。当上述参数发生变化时，系统的输出功率和传输效率也会随之变化。通常，谐振线圈在工作中,其电感和等效电阻被视为常量。电源内阻一般也被视为常量。因此，MCR-WPT系统的输出功率和传输效率主要由ω、M和RL决定。

2 MCR-WPT系统传输特性研究

由输出功率和传输效率的表达式可知，电能传输系统的输出功率和传输效率受多个不同参数影响，故采用单一变量控制法，使用MATLAB进行仿真分析不同参数对系统的影响。

2.1 传输特性与电源频率的关系

谐振状态下,频率对系统输出功率与传递效率的影响结果如图2所示。由图2可知，随着系统频率f的增加，系统输出功率呈现先快速增加后缓慢降低的变化过程，即系统存在最大功率点；而系统传递效率随着频率的增加一直增加，最高可达90%以上。系统频率对电能传输影响重大，系统固有频率过低会导致输出功率小、传递效率低；系统固有频率高会大幅提高系统的传递效率，但对输出功率提升不明显，而且系统频率越高对电路元器件的要求也越高，相应的成本也越高。

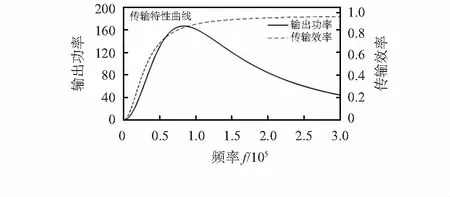
图2 频率对系统传输特性的影响

2.2 传输特性与耦合系数的关系

耦合系数K表示发射线圈与接收线圈耦合的松紧程度，是影响MCR-WPT系统输出功率和传输效率的重要因素。谐振状态下，耦合系数对系统输出功率与传递效率的影响结果如图3所示。

图3 耦合系数对系统传输特性的影响

由图3可知，谐振状态下，耦合系数K从0增长至1的过程中，系统的输出功率呈现先快速增加后缓慢减低的变化过程，并且在耦合系数K=0.15附近输出功率取得最大值。在最大功率点周围曲线变化的幅度比较大，为保证系统工作在大功率状态，在设计系统时需注意耦合系数的设定。

2.3 传输特性与负载的关系

谐振状态下，负载对系统传输功率和传输效率的影响如图4所示。由图4可知，谐振状态下，随着负载阻值递增，系统输出功率和传输效率均呈现出先增加后减小的变化趋势，即系统最大功率点和最大效率点均存在，但系统最大功率点和最大效率点所对应的负载阻值不同，即不存在最优负载使系统同时工作在最大功率状态和最大效率状态。

图4 负载阻值对系统传输特性的影响

3 基于改进SSA的效率优化

3.1 SSA

SSA是受自然界中麻雀觅食行为与反捕食行为启发而提出的群体智能优化算法[11]。

在SSA中，发现者位置更新公式为

(7)

麻雀种群中的追随者会时刻监视发现者的行动，一旦观测到发现者找到食物更充足的地点，便会离开当前位置去争夺食物，追随者的位置更新公式为

(8)

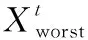
麻雀种群中侦查者的产生随机性，其位置更新公式为

(9)

3.2 改进策略

3.2.1 基于Tent混沌反向学习的初始化策略

混沌是非线性系统中普遍存在的一种现象，是一种看似随机的伪随机运动，具有随机性、规律性及遍历性等特点。常见的有Tent映射、Logistic映射两种混沌系统，文献[12]验证了Tent映射具有更好的遍历均匀性。Tent映射迭代公式为

(10)

式中b∈(0,1)，Xn[0,1]，n=1,2,3,…,n。

本文采用Tent映射生成 分布相对均匀的初始解，然后使用反向学习[13]对每个初始解产生相应的反向解。将初始解与反向解进行对比，筛选出适应度较好的N个个体作为初始种群，并得到分布更加均匀的初始种群。基于混沌反向学习策略对初始种群的初始化可以提高初始解的质量和精度，有助于提升算法的性能。

3.2.2 基于莱维飞行行为的改进策略

莱维飞行是一种服从莱维分布的随机搜索方法，是自然界中生物觅食的理想方法。利用莱维飞行中的频繁短距离搜索与偶尔长距离搜索混合式的搜索方式可增强算法的全局搜索能力，防止算法陷入局部最优解[14～16]。

基于莱维飞行的位置更新公式为

(11)

式中xi(t)为第t代的第i个解；l为控制步长的权重；Levy(λ)为随机搜索路径，满足Levy(λ)～u=t-λ，1≤λ≤3。

根据Mantegna算法求得莱维飞行的路径表达式为

(12)

式中μ和ν服从正态分布(γ为常数)，其定义如下

(13)

式中γ=1.5。

融合莱维飞行后的追随者位置更新公式为

(14)

3.2.3 高斯与柯西变异

高斯变异和柯西变异是两种常用的扰动方式，图5为它们的概率密度函数比较图。

图5 标准高斯分布、柯西分布的概率密度曲线比较

由图5可知，柯西概率密度函数图像两端形状较长，趋于0的过程中变化比较平缓，可以使个体有能力跳出局部最优解，且变异产生的子代与父代差异性更大，故柯西变异的扰动性更强；而高斯变异的重点搜索区域是原个体附近的局部区域，有利于算法快速、精确地搜索到全局极小值点。因此，算法前期采用柯西变异，可以避免算法陷入局部最优解；算法后期采用高斯变异，可以进行细致的局部搜索，加快算法的收敛速度。

3.3 改进SSA

根据前文改进策略得到的改进SSA求解MCR-WPT系统传输效率优化问题，具体步骤如下：

Step 1 初始化参数，如种群数量N,最大迭代次数Max_iter,发现者比例PD,侦查者比例SD,目标函数维度D,初始值的上下边界lb、ub，并应用混沌反向学习初始化麻雀种群。

Step 2 根据目标函数计算麻雀个体的适应度值，找到当前最优适应度及其对应的位置和当前最劣适应度及其对应的位置。

Step 3 按设定的比例选取适应度较好的麻雀作为发现者，剩余麻雀作为追随者，并按照式(6)和式(7)对种群中的发现者和追随者进行位置更新。

Step 4 在麻雀种群中按比例随机选择部分麻雀个体作为侦查者，并按照式(8)对侦查者进行位置更新。

Step 5 根据当前迭代次数t进行柯西高斯扰动。

Step 6 迭代完成后，重新计算麻雀种群个体最优与最差适应度值及其对应的位置。

Step 7 判断算法当前迭代次数是否已到达最大迭代次数Max_iter。若是，则输出种群最优适应度值作为最优目标值，最优适应度值对应的麻雀位置作为最优目标解；反之，则转入Step 3继续运行算法。

3.4 改进SSA在效率优化中的应用

采用改进SSA实现MCR-WPT系统输出特性优化是一个以系统输出效率为目标函数，以频率、耦合系数和负载阻值为解空间的三变量单目标寻优过程。

1)选取优化变量

将前文分析过的影响系统传输效率的三个参数—频率f,耦合系数K,负载阻值RL作为优化变量，即

(15)

2)建立目标函数

将系统的传输效率定义为适应度函数，适应度函数表达式为

(16)

(17)

ω=2πf

(18)

(19)

将上述目标函数和约束条件在MATLAB软件中进行编写，运行算法即可搜索适应度函数的最优解。

4 仿真分析

在MATLAB中将改进SSA的迭代次数设为50,发现者比例PD设为0.3,侦查者比例SD设为0.2。利用改进SSA计算得到选定的最优参数为[80 kHz,0.2,12Ω]，即当工作频率为80 kHz，耦合系数为0.2，负载阻值为12 Ω时，系统的传输效率达到最大值。图6为MCR-WPT系统的适应度函数的收敛图。

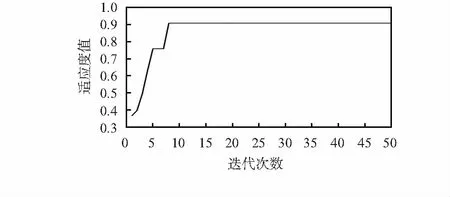
图6 适应度函数的收敛图

由图6可知，算法在8次迭代后，系统的传输效率基本稳定在0.91，且最优解对应的频率在系统最大功率点所对应的频率附近，即输出功率在最大功率点附近，证明了改进SSA在保证输出功率的情况下提高了MCR-WPT系统的传输效率。

为了验证优化方法的准确性，在Simulink中改变频率、耦合系数与负载的仿真值进行多次实验。将频率仿真值分别取75,80,85，耦合系数仿真值分别取0.1,0.2,0.3与负载仿真值10,12,14进行仿真试验结果如图7所示。

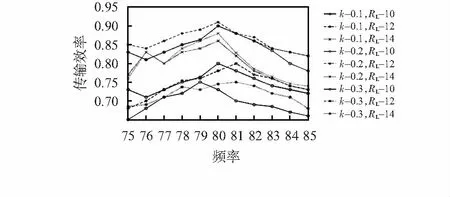
图7 仿真实验

由图7可知，改变系统的频率f,耦合系数K和负载RL均会影响系统的传输效率，且系统传输效率在所求最优参数可取得最大传输效率，证明了上述改进算法对MCR-WPT系统传输效率提升的可行性。

5 结 论

本文利用互感耦合理论对MCR-WPT系统进行系统的理论分析，在MATLAB中对影响MCR-WPT系统传输效率的重要因素进行仿真分析，为MCR-WPT系统的设计提供了理论指导。

以提高MCR-WPT系统的传输效率为目标，对系统多参数之间的匹配问题进行优化，使得系统工作在最佳传输效率状态。首先利用MATLAB仿真软件对影响MCR-WPT系统效率的3个关键参数—频率、耦合系数、负载阻值进行研究；然后以MCR-WPT系统的传输效率为适应度函数，通过改进SSA对适应度函数进行寻优，得到了最优解对应的参数值。仿真结果表明，改进SSA可以较快地对影响系统传输效率的3个重要参数进行寻优，即较快地使系统传输效率达到最优。