硅MEMS光纤法珀振动传感器的温度解耦分析*

钱 江, 秦 丽, 贾平岗, 任乾钰, 刘 华, 熊继军

(中北大学 仪器科学与动态测试教育部重点实验室,山西 太原 030051)

0 引 言

在过去的20年,高温振动传感器在航空航天、能源勘探、天然气管道运输、核反应堆和汽车环境中发挥着重要作用[1-3]。与传统的电学传感器相比,光纤传感器具有抗电磁干扰和光干涉不受温度影响的优点,已被广泛研究[4-6]。其中，基于MEMS技术的光纤法珀(Fbry-Pérot，F-P)振动传感器,由于体积小、一致性高、可批量化等优点受到广泛关注[7-9]。然而,在高温环境中，组成光纤MEMS传感器的各部分结构由于材料的热膨胀以及弹性模量等力学参数改变，其测量精度发生了很大偏差。为了解决这一问题,通常将一个温度传感器集成在光纤传感器上,从而实现温度—被测参数同时测量。中北大学Jia P G等人在硅MEMS光纤F-P压力传感器中集成了光纤布拉格光栅(FBG),利用FBG的温度敏感性实现了温度—压力的同时测量[10]。天津大学Yin J D等人在硅MEMS光纤F-P压力传感器中集成了受温度敏感的Pyrex玻璃晶片,利用Pyrex玻璃镜片厚度受温度变化而变化的特性,完成了温度—压力的同时测量[11]。

本文针对硅MEMS光纤F-P振动传感器的结构,利用硅材料在C波段的透光性,以振动传感器敏感单元中的质量块作为温度测量单元,在不改变原有的加工工艺的前提下,利用F-P多腔干涉光谱进行互相关计算,得到质量块的光学厚度,并通过20～400 ℃的温漂实验,获得了振动传感器的零漂与温度变化一一对应的关系,同时,通过拟合加速度的灵敏度与温度的关系,结合振动传感器的零漂,设计温度解耦算法对加速度的温度交叉灵敏度进行解耦,并将不同温度下解耦后的加速度值与实际加速度值进行线性度评估,得到振动传感器的测量非线性误差不大于1.316 7 %。

1 工作原理

1.1 硅MEMS光纤F-P振动传感器的工作原理

硅MEMS光纤F-P振动传感器的结构如图1所示。光纤通过硼硅玻璃毛细管集成在敏感头上,敏感头由上层硼硅玻璃外壳,硅敏感单元以及底层硼硅玻璃基座组成。弹簧—质量—阻尼系统由硅敏感单元上的四根完全相同的硅梁以及硅梁中间的质量块组成,质量块的厚度比硅梁的厚度大。单模光纤通过硼硅玻璃毛细管与传感头上的凸台集成,单模光纤端面与质量块上表面以及质量块下表面形成多腔F-P干涉,分别对应两个F-P腔LFP1和LFP2的位置。光纤端面的反射率为R1,质量块上表面的反射率为R2,质量块下表面的反射率为R3。

图1 硅MEMS光纤F-P振动传感器结构示意

根据牛顿第二定律和欧拉—伯努利梁理论,传感器的灵敏度可以表示为

(1)

式中m为中心质量块质量；l,b,h分别为梁的长、宽、高；E为硅材料的弹性模量；g为一个重力加速度；S的单位为nm/gn。

根据图1,多腔干涉的入射光与反射光强度的关系为

(2)

式中Ir为反射光强度；R1、R2和R3为3个反射面的反射率；θ1=4πn1LFP1/λ和θ2=4πn2LFP2/λ分别为第一束反射光与第二束反射光之间、第二束反射光与第三束反射光之间的相位。

由式(2)可得,当振动传感器的结构与材料确定后,振动传感器光谱输出与LFP1和LFP2有关。

当该振动传感器的环境温度发生变化时,由式(1),振动传感器的在温度T下的灵敏度可以表示为

(3)

式中E(T)为硅材料随温度变化的弹性模量。若忽略温度对梁尺寸的影响,则式(3)反映了振动传感器的灵敏度随温度的变化关系。硅的弹性模量随温度的升高而升高[12],则该振动传感器的灵敏度随温度的升高而升高。传感器结构受温度变化如图2所示,LFP1和LFP2均发生变化。在不考虑半波损耗的前提下对式(1)进行仿真,可得传感器的光谱如图3所示。图3(a)为改变第一个干涉腔长的光谱变化,图3(b)为改变第二个干涉腔长的光谱变化。从图中可以看出,两个干涉腔的干涉光谱发生了叠加,为了更好地区分两个腔对应的光谱,LFP1设置为20 μm,LFP2设置为300 μm。当只改变LFP1时,光谱中的大包络发生横向偏移,而小波的相位则没有发生改变。当只改变LFP2时,光谱中的大包络为发生偏移,而小波的相位则发生了改变。对于高温下的振动加速度来说,当环境温度不发生改变的情况下,LFP2不发生改变,而LFP1会对振动加速度产生响应,且响应频率高。当环境温度发生改变时,LFP2会对温度产生响应,相对于振动加速度来说,这种响应频率低。因此,当解调LFP1振动加速度的响应时采用腔长变化量解调的方法,如双波长解调方法时,可以避免LFP1由温度引起的响应。而振动加速度不会引起LFP2的响应,因此,测量LFP2可以得出当前振动传感器所处的温度值。

图2 温度对两个腔长影响示意

图3 多腔干涉光谱仿真

1.2 温度解耦方法

对多腔干涉光谱进行LFP2的提取,利用互相关算法对滤波后的干涉光谱进行解调[13,14]。已知光谱序列滤波后的S(n),模拟一个干涉光谱信号Sv,再将两个光谱序列进行卷积得到互相关系数,再调整Sv中的dv参数在LFP2附近取范围,得到最大互相关系数对应的dv，即为质量块的光学厚度

(4)

采用上述方法分别对不同温度下的LFP2进行测量可以完成对LFP2与温度的拟合关系。

对制作好的加速度计分别进行温度—振动复合实验测试,加速度解调系统为双波长解调系统,通过调整光源与光滤波器使干涉只发生在短腔(LFP1)中从而直接测量LFP1由于振动加速度而产生的腔长变化量[15]。因此，该解调结果只对振动加速度响应。当外界存在一定温度且没有振动激励时,通过光纤光栅解调仪获得振动传感器的光谱数据,包含大包络和小波的相位信息,对小波的相位进行分析可以得到LFP2。通过对不同测试温度下的LFP2进行拟合,得到LFP2与温度的对应关系；当外界存在已知温度和振动加速度激励时,采用双波长解调系统进行解调,测得振动传感器在不同温度下加速度灵敏度差异,由于传感器具有输出相位峰峰值大小与外界加速度大小呈线性关系的特点,所以，对振动传感器在标定温度时的相位输出数据进行线性拟合,得到振动传感器在此温度下加速度响应的灵敏度S(T)。设温度T下的LFP2(T)和灵敏度S(T)与温度的函数关系分别为

LFP(T)=α(T)

(5)

S(T)=β(T)

(6)

式中α,β分别为LFP2,S(T)与温度的函数拟合关系。

因为振动传感器在温度T下的灵敏度与外界加速度变化呈线性,所以可用一次函数来表达二者之间的关系,而解调是对腔长变化量的解调,因此，可以得到振动传感器的零漂随温度变化不影响传感器的灵敏度,即一次函数的截距为零。设一次函数表达式为

φT=ST·a

(7)

式中φT和a分别为温度T下传感器对外界加速度的响应峰峰值和外界加速度。

在某一时刻,已知振动传感器的输出峰峰值φT,LFP2的值以及LFP2与温度的对应关系,将LFP2代入式(5)中得到此时对应的温度T,再将温度T代入到式(6),可以得到振动传感器的灵敏度S(T),再将S(T)代入到式(7)中得到传感器的相位峰峰值与外界加速度之间的一一对应的关系,即可得到此温度下的外界加速度值。

这种温度解耦方法虽然需要对传感器进行预先的标准化测试,但不需要进行全温区下的振动测试标定,经过温度解耦之后的传感器在使用过程中可应用在任意未知的温度场合,不需根据当时环境温度再次进行传感器的标定。

2 传感器加工

如图4(a)～(d)将清洗后的硅片前预处理(烘涂黏附剂),采用AZ4620光刻胶,通过光刻工艺将对准标记及梁—质量块结构图形化,利用深硅刻蚀工艺进行刻蚀,刻蚀深度为90 μm；在硅片背面再次进行均胶,通过背套光刻将质量块结构图形化,进行二次深硅刻蚀工艺,刻蚀深度为210 μm,将梁—质量块结构释放出来。采用CNC加工硼硅玻璃盖板和背板如图4(e),(f),再将带有敏感结构的硅片与盖板和背板进行阳极键合如图4(g)。将键合好的圆片进行CNC加工凸台后进行划片完成传感头的分离如图4(h),再用CO2激光熔接将光纤集成在传感头上,如图4(i)。

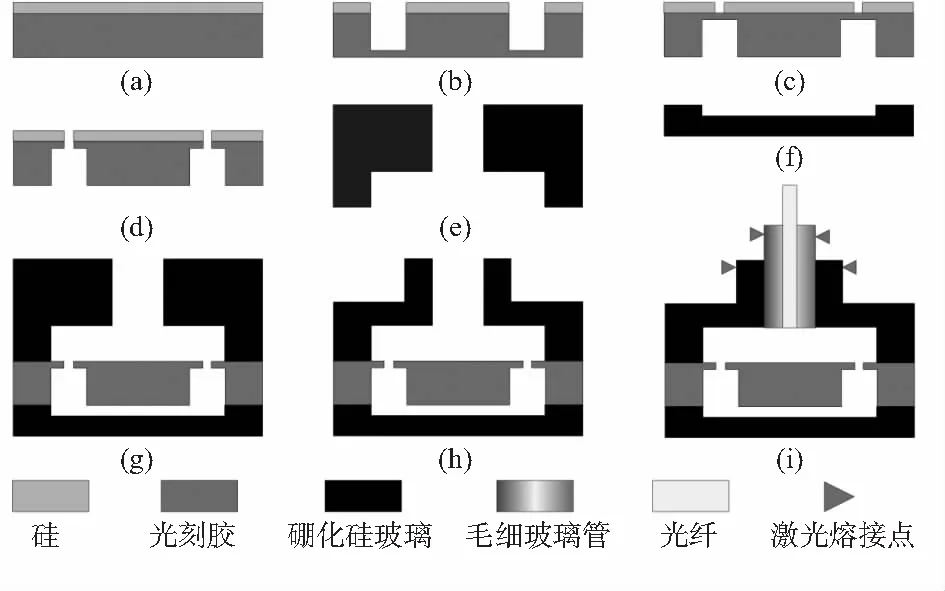
图4 硅MEMS光纤F-P振动传感器工艺流程

加工好的振动传感器光谱如图5所示,信号强度为-16 dB左右,对比度为43 dB左右。从图中可以看出:光谱由一个大包络LFP1和小波LFP2叠加而成,从加工过程中可知质量块厚度与硅晶圆厚度一致,为300 μm。

图5 硅MEMS光纤F-P振动传感器干涉光谱

3 实验结果

图6(a)为振动传感器在100，200，300，400 ℃下未受振动加速度激励的光谱,可以看出：光谱随温度的升高而向右移动。分别对振动传感器在20～400 ℃下的光谱进行互相关计算得到LFP2的光学厚度,结果如图6(b)所示,对图中数据进行曲线拟合得到LFP2的光学厚度与温度之间的关系,曲线拟合度为99.955 %。

图6 硅MEMS光纤F-P振动传感器的光学厚度与温度的关系

分别在每个温度下对振动传感器输出峰峰值进行记录,得到的斜率即为各温度下的振动传感器的灵敏度,如图7(a)所示。将各温度下的灵敏度值单独提取出来得到温度交叉灵敏度,如图7(b)所示。对该结果进行三次函数拟合,得到振动传感器的灵敏度与温度变化关系为

S(T)=A+BT+CT2+DT3+ET4

(8)

式中A=0.036 74,B=1.394 82×10-4,C=5.566 233×10-7,D=-6.390 35×10-9,E=1.239 04×10-11,曲线拟合度为97.401 %。

图7 硅MEMS光纤F-P振动传感器的灵敏度随温度变化关系

已知各温度下振动传感器的响应峰峰值φT,将φT与式(7)代入式(6)可以得到解耦后的传感器测得的加速度值。图8显示了各温度下解耦后的加速度值与实际加速度值的比较。由图8可以看出,在20,100,200,300，400 ℃时,各温度下的计算值与激振台的实际加速度值温吻合良好,只存在微小的误差,最大误差分别为22,2,18,16，14gn,非线性误差分别为1.185 5 %,1.227 3 %,0.931 4 %,1.316 7 %和1.041 1 %,计算值拟合曲线的斜率分别为0.998 96,1.000 06,0.999 06,0.999 89和1.000 11,斜率都非常接近于1。

图8 20～400 ℃温度解耦结果

4 结 论

本文提出了一种硅MEMS光纤F-P振动传感器结构，根据其灵敏度随温度变化的趋势,设计了一种采用质量块作为温度集成单元的结构进行温度解耦。利用光谱互相关算法得到质量块的光学厚度与温度的关系,对振动传感器的灵敏度进行温度标定。最后利用温度解耦算法对振动传感器在不同温度下的温度交叉灵敏度进行修正得到解耦后的测量加速度值。根据解耦结果,振动传感器测量的最大误差在1.316 7 %以内。