考虑拱架效应和后壁剪切力的充填体强度模型

瞿晨明

(山东科技大学 能源与矿业工程学院，山东 青岛 266590)

随着充填采矿法的广泛应用，矿山采空区充填体的稳定性问题日益突出，成为影响矿山安全生产的重要因素。在采场中，充填体的强度不足，无法起到充填采空区、支撑采场顶板作用，甚至会引起严重的安全事故，造成财产损失和人员伤亡；另一方面，充填体的强度过大，则会增加充填成本，经济效益较差[1].因此，对于充填体的合理强度预测研究具有一定的现实意义。目前胶结充填体常用计算方法有Terzaghi模型、Thomas模型、Mitchel模型和安庆铜矿经验公式等[2].曹帅等[3]基于弹性平面应变假设，建立阶段嗣后胶结充填体矿柱强度模型并进行求解分析；吴爱祥等[4]基于计算拱架效应对直应力的转化比，得到窄长型充填体的强度公式；胡世利等[5]根据傲牛铁矿现状，建立矿房充填体力学模型，分析计算出充填体极限自立高度和充填体内力分布；杨蕾等[6]根据岩体开挖释放能量与充填体峰值变形能相近的原则，得到与岩体相匹配的充填体强度匹配公式；周乐等[7]将单侧暴露下充填体简化为平面应变问题，推导得出底部剪应力公式，以确定充填体自立强度；刘光生等[8]基于Marston拱应力二维模型建立了三维拱应力充填体解析模型并进行对比验证分析。上述国内外研究成果多针对充填体尺寸和物理参数对充填体强度设计进行了优化，但并未充分考虑拱架效应和实际工程中充填体与后壁围岩之间剪切力的影响。本文将充分考虑充填体与围岩之间相互作用，建立单侧暴露胶结充填体三维强度力学模型，并应用于工程进行验证，分析充填体尺寸及物理参数对充填体强度的影响。

1 经典胶结充填体强度力学模型

目前，国内外胶结充填体力学强度模型通常采用经验类比法和力学模型分析法[9]，通过对充填体的力学状态及围岩之间相互作用的机理分析，总结出经典的胶结充填体计算方法。

1.1 Terzaghi强度模型

土力学奠基人Terzaghi在1943年提出了太沙基理论[10]，该理论假定了岩体为具有一定黏聚力和内摩擦角的散体。其表达式为：

(1)

式中，σv为充填体的设计强度，kPa；γ为充填体的容重，kN/m3；L为充填体的长度，m；c为充填体的黏聚力，kPa；φ为充填料的内摩擦角，(°)，K为岩体侧压力系数。

1.2 Thomas强度模型

该方法考虑了在实际工程中充填体与围岩由于摩擦效应所产生的拱架效应，得到了作用在充填体强度设计公式：

(2)

式中，H为充填体的高度，m；W为充填体宽度，m.

1.3 安庆铜矿经验公式

通过对安庆铜矿某高阶段大直径深孔采场中充填体进行应力监测，得到大量数据后结合室内试验和数值分析综合模拟，得到了半经验强度设计公式，其充填体强度计算经验公式[11]为：

(3)

1.4 Mitchell强度模型

Mitchell等人认为胶结充填体与围岩之间产生的剪切力承担了充填体的部分重力载荷和充填体上覆岩层载荷，并忽略了充填体与矿体的剪切力，利用极限平衡法，提出强度公式：

(4)

式中，α为充填体潜在滑移面与水平面的夹角，α=45+φ/2，(°)；F为安全系数，取1.5.

2 考虑拱架效应和后壁剪切力的充填体强度模型

2.1 基本假定

拱架效应[12]是指由于充填体与围岩，矿体之间产生的摩擦效应阻止其因自重而下沉，加之因充填体内部所产生的水化作用下充填体与围岩，矿体之间产生黏结作用，在水平应力作用下，在充填体内出现垂直应力小于自重的现象(图1).

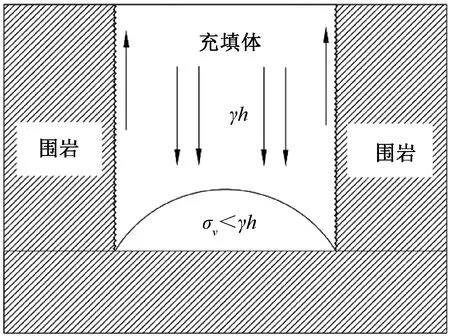
图1 充填体拱架效应示意图

考虑拱架效应和后壁剪切力的充填体强度模型(以下简称本文强度模型)，为方便计算，做出如下假设：1)选取的充填体采用同一种充填材料，且充填体内部各向同性。2)忽略充填体充填工程中的时间效应和施工工序。

2.2 力学计算

取厚为dh的水平单元体进行受力分析(图2)，求解围岩与充填体之间的垂直应力σv.该水平单元受到自重G、两侧剪切力Q1和Q2、后壁剪切力Q3、竖向力V和V+dV共同形成平衡力系[13].

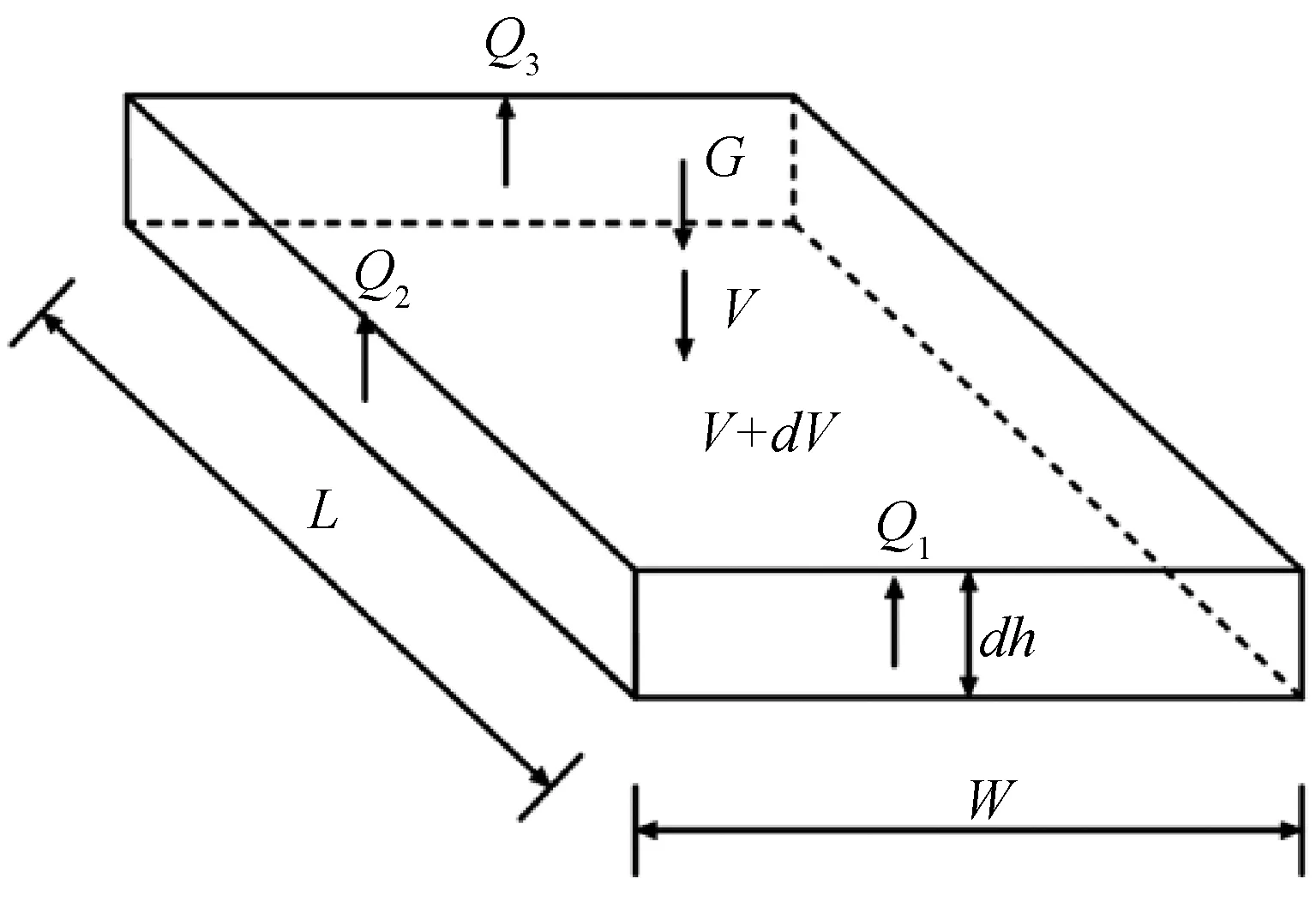
图2 考虑拱架效应和后壁剪切力的充填体强度模型图

单元体的自重P为：

G=γLWdh

(5)

dV=LWdσv

(6)

依据莫尔-库仑准则，胶结充填体水平单元体与围岩接触面上剪切力可按照式(7)计算：

τs=cs+σhtanδs

(7)

式中，cs为胶结充填体与围岩间的黏聚力，kPa；δs为胶结充填体与围岩间的摩擦角，(°).一般情况下，充填采场中与胶结充填体与围岩，矿体接触面上的黏聚力和内摩擦角可按照式(8)、(9)进行计算取值[14]：

ci=aic

(8)

δi=biφ

(9)

式中，ai和bi分别为胶结充填体与围岩接触面上的黏附系数和内摩擦系数。

将式(8)、(9)代入公式(7)，可得方程：

Q13=τ13Wdh=(σhcσvtanb13φ+a13c)Wdh=

(K13σvtanb13φ+a13c)Wdh

(10)

Q2=τ2Ldh=(σhctanbiφ+aic)Ldh=

(Kiσvtanbiφ+aic)Ldh

(11)

式中，Ki为充填体与围岩的侧压力系数，Ki=σh/σv.事实上，经过许多理论计算结合现场实验得知，充填体与围岩，矿体间的侧压系数介于充填体的主动侧压力下系数和静止侧压力系数之间[15].为了简化计算，选取主动侧压力系数下进行计算，则有：

(12)

由力的平衡可以得到该水平层单元体的垂直方向的平衡方程：

G=dV+2Q13+Q2

(13)

将式(5)、(6)、(10)、(11)代入式(13)可得：

(14)

在一般矿山生产中，充填体所接触采场的上下盘围岩接触面的力学特性相似[16]，即充填体与上下盘围岩接触面上的黏聚力和内摩擦角近似相等(即a13=a2，K13=K2，b13=b2)，所以根据边界条件，当h=0时，σv=0，计算可得到考虑拱架效应和后壁剪切力的胶结充填体的强度设计公式：

(15)

3 工程算例应用分析

山东华联矿业股份有限公司卧虎山矿区矿体呈多层条带状，排列紧密，矿体产状与顶底板围岩一致，边界清晰。矿带夹层多，复合缺失现象明显，矿体极不连续。卧虎山矿区目前采用一、二步矿房交替上升式充填采矿法。而在该充填采矿法中，一步矿房开采胶结充填再进行二步矿房回采时，胶结充填体会出现单侧暴露的开采状态，该胶结充填体的稳定性便成为采场安全开采的关键。

3.1 充填体结构参数对强度预测值的影响分析

一步矿房胶结充填体暴露长度L=35 m，宽度W=11 m，暴露高度H=13.6 m，胶结充填体与围岩间接触面上的黏附系数取0.4，内摩擦系数取值0.8[17]，卧虎山矿区采用的矿体、胶结充填体和非胶结充填体的物理参数见表1.一步矿房充填体尺寸以及充填体黏聚力和内摩擦角对5种充填体强度模型影响变化规律见图3—7.

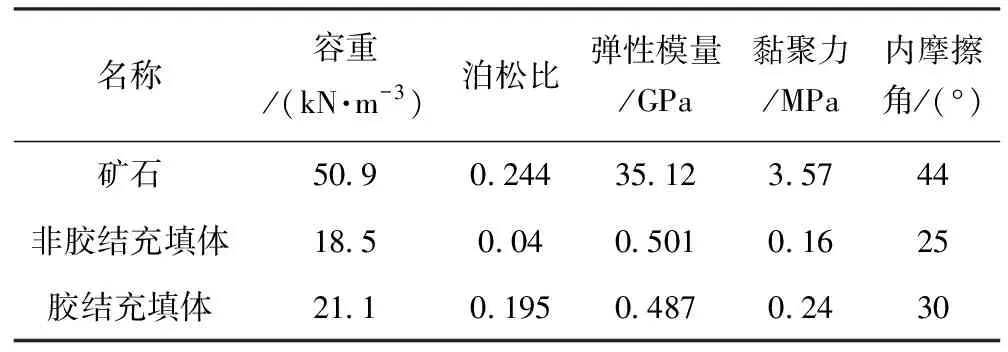
表1 矿石与充填体物理力学参数表

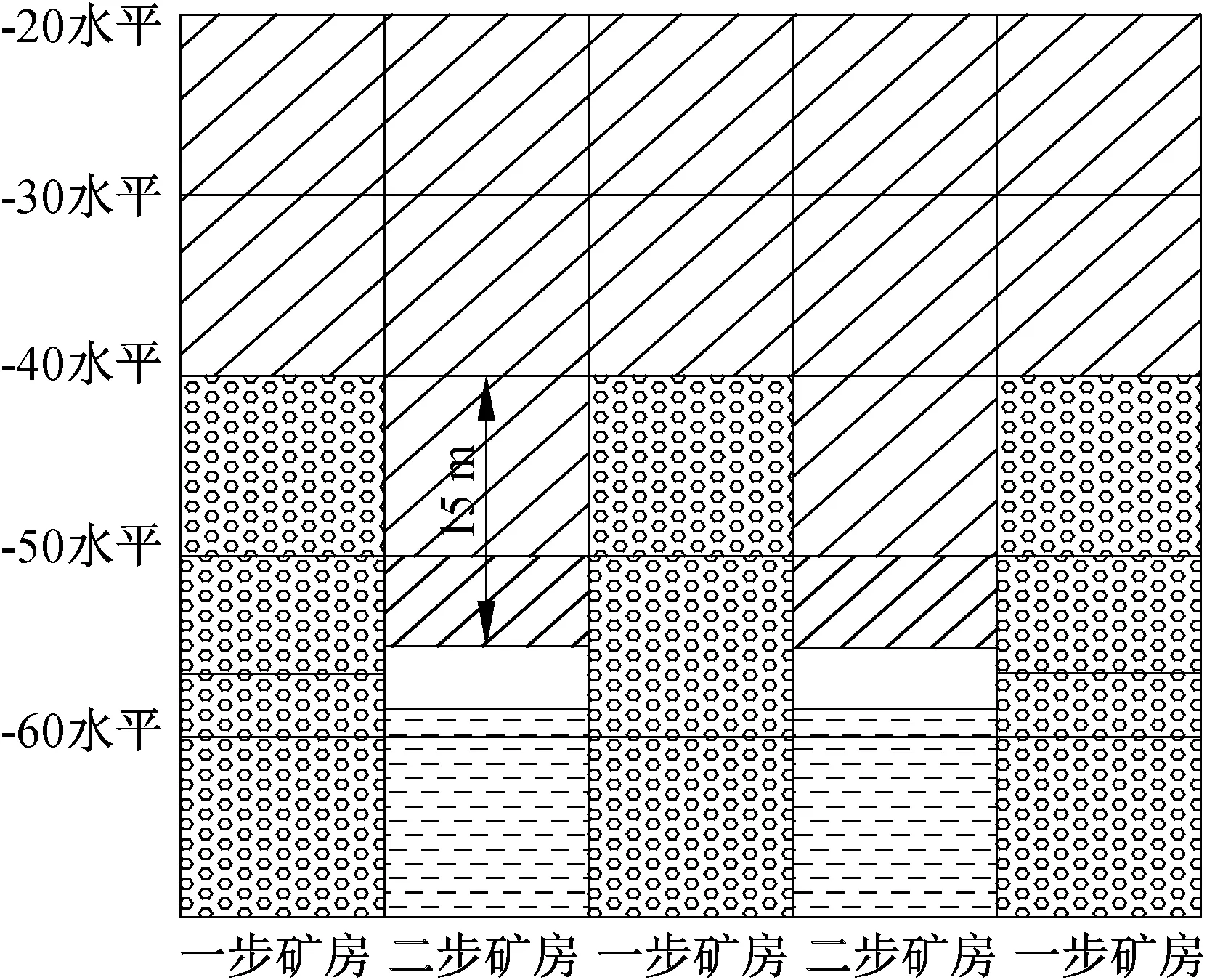
图3 矿房交替上升式充填采矿法图

一步矿房胶结充填体单侧暴露情况下，5种充填体强度计算模型随着充填体暴露高度影响分布规律见图4.由图4可以看到，5种充填体强度模型预测值均随着充填体暴露高度的增加而上升，其中安庆铜矿经验公式强度预测值最高，Thomas强度模型强度预测值曲线变化最平滑缓慢；在充填体高度小于24.5 m，Thomas强度模型预测值大于Terzaghi强度模型预测值，原因是Terzaghi强度模型考虑拱架效应对充填体自重应力的影响，使得预测值偏小，而充填体高度大于25.5 m时，充填体自重应力增幅大于拱架效应的可承担应力的增幅，使得Terzaghi强度模型预测值大于Terzaghi强度模型预测值；本文强度模型曲线随着暴露高度的增加缓慢增加，强度预测值低于Thomas强度模型等。

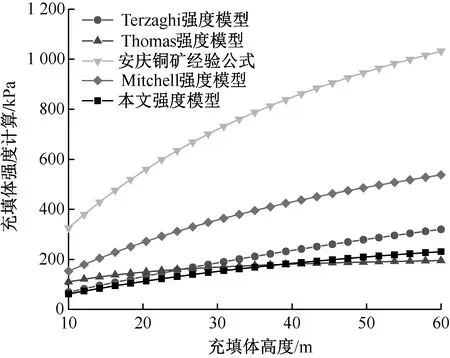
图4 充填体高度对充填体强度预测值的影响图

由图5可知，Thomas强度模型与本文强度模型曲线是随充填体宽度增加而缓慢增大；因Terzaghi强度模型和Mitchell强度模型与充填体宽度无关，二者强度模型曲线无明显变化；安庆铜矿经验公式强度预测值最大，与充填体宽度呈现负相关。

图5 充填体宽度对充填体强度预测值的影响图

由图6可知，随着充填体长度的增加，Mitchell强度模型、Terzaghi强度模型、安庆铜矿经验公式和本文强度模型预测值呈缓慢上升趋势，其中Mitchell强度模型预测值的增长缓慢，说明充填体长度对其影响较小；本文强度模型预测值总体低于Terzaghi强度模型等预测值，Terzaghi强度模型充分考虑与侧壁围岩接触形成的拱架效应，在一定充填体长度范围内能够保持自稳；充填体长度对Thomas强度模型无影响。

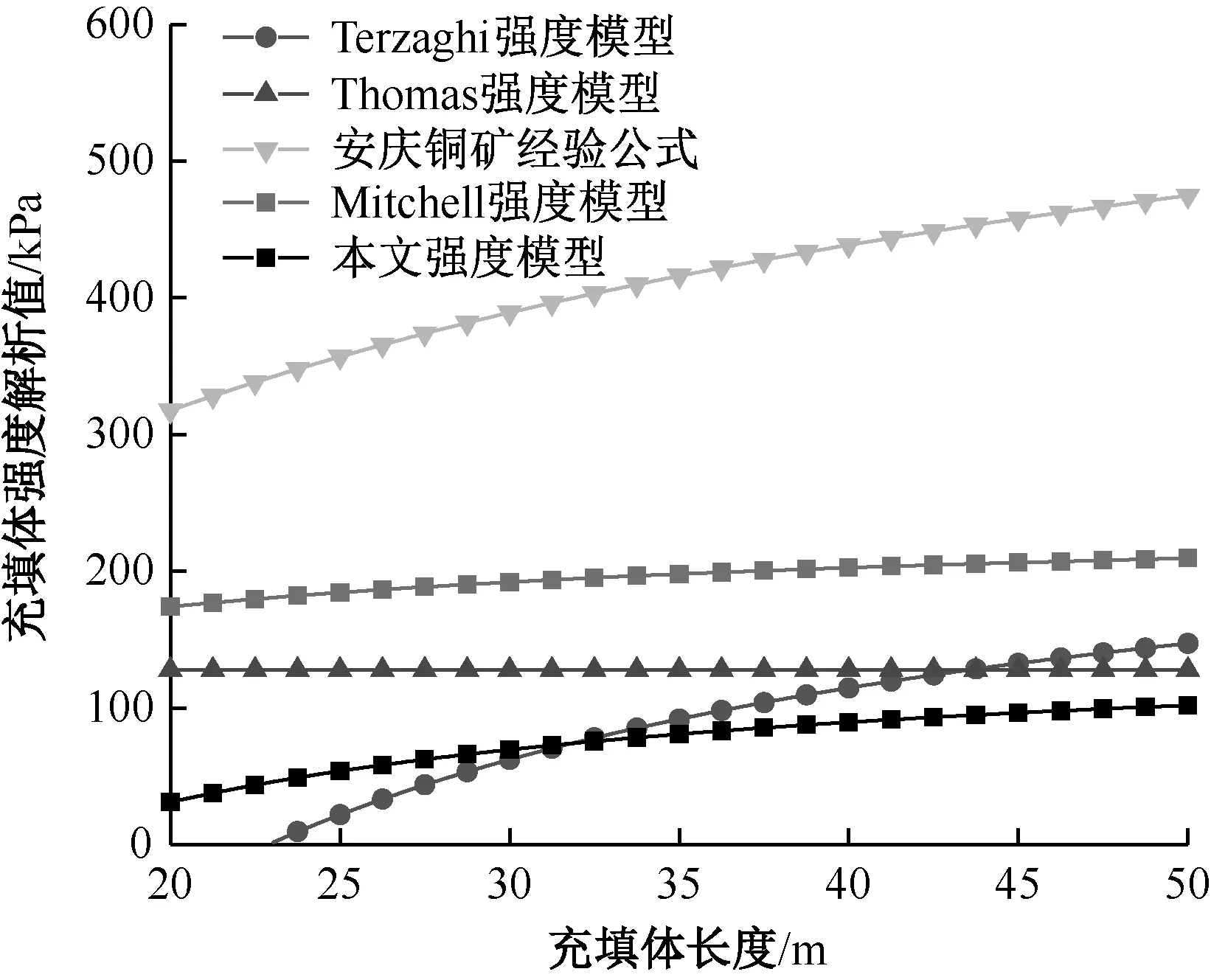
图6 充填体长度对充填体强度预测值的影响图

3.2 充填体与接触面参数对强度预测值的影响分析

由图7可知，Terzaghi强度模型与本文强度模型的预测值随着充填体黏聚力的增加而下降，呈现负相关，Terzaghi强度模型是将充填体近似看成拥有一定黏聚力和内摩擦角的固结土，黏聚力对充填体强度大小起主导作用；本文强度模型预测值则是充分考虑了侧壁与后壁的剪切力，使得强度预测值小于Terzaghi强度模型，与其近似平行；因Thomas强度模型、Mitchell强度模型和安庆铜矿经验公式均未充分考虑胶结充填体与围岩接触面的黏接作用，三者计算强度预测值曲线无变化。

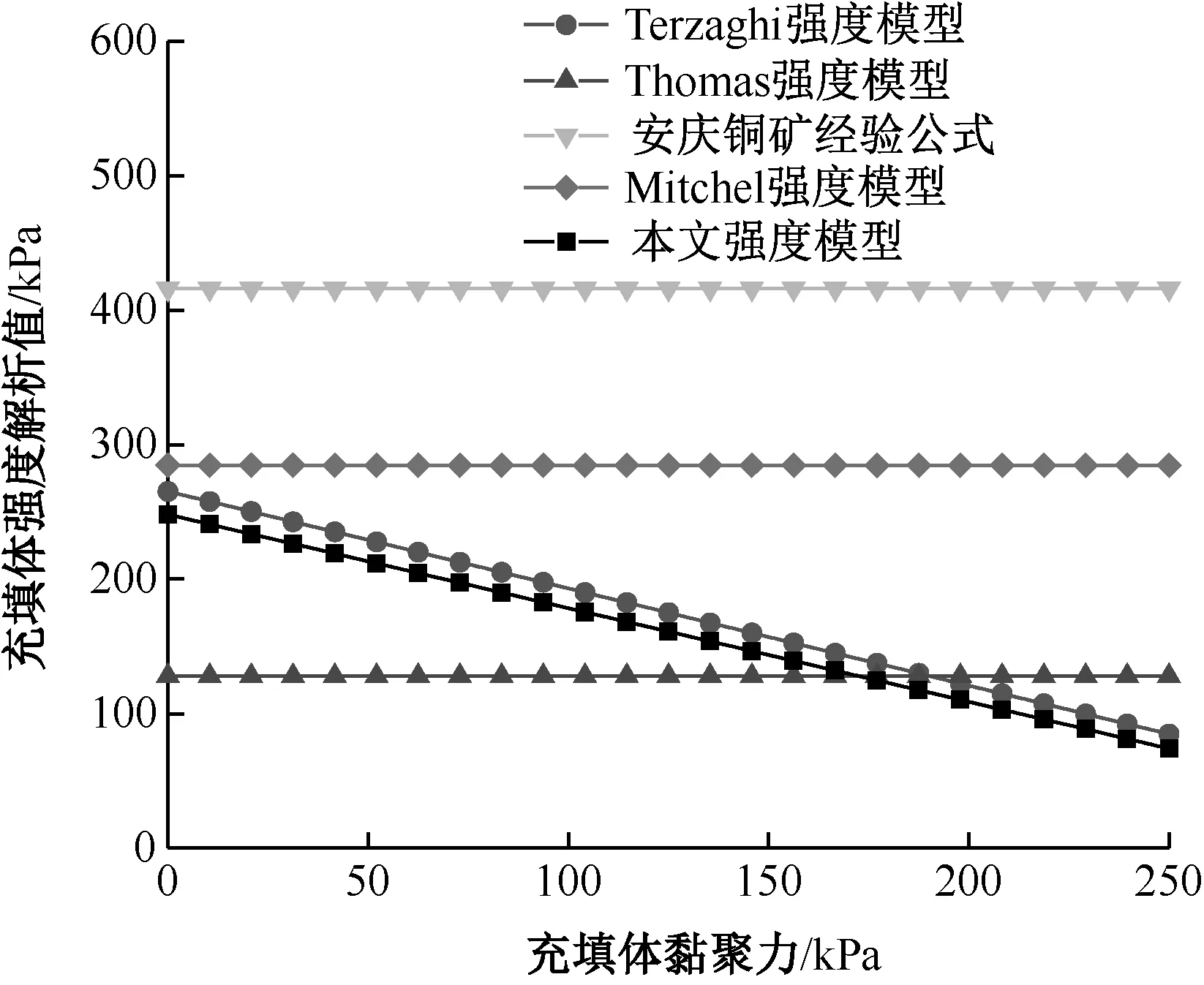
图7 充填体黏聚力对充填体强度预测值的影响图

充填体与围岩接触面对充填体强度的影响见图8.通过图8可以看出，当黏附系数为0.1时，也就是充填体与围岩接触面较为光滑，粗糙程度低，随着充填体内聚力的增大，本文强度计算预测值变化不明显；黏附系数为1.0时，充填体与围岩接触面不平整，粗糙程度高，随着充填体内聚力的增大，本文强度计算预测值大幅下降。相同的，充填的不同的内摩擦角系数的取值对于本文强度计算预测值与不同的黏附系数取值趋势相同，但预测值的变化范围较小。

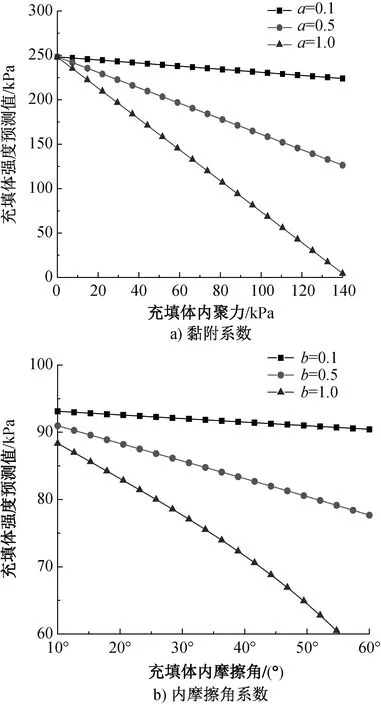
图8 充填体与围岩接触面对充填体强度的影响图

在金属矿山中多以爆破开采为主，加之围岩的节理发育、风化程度、含水量等因素影响，充填体与围岩，矿体的接触面粗糙且不平整。接触面的粗糙程度越高，黏附系数和内摩擦角系数越大，胶结充填体内所产生的拱架效应和后壁围岩接触面摩擦效应越明显。

综上所述，Mitchell强度模型对充填体高度变化比较敏感，安庆铜矿经验公式受因素影响较多，适用于偏安全的保守计算，Thomas强度模型与Terzaghi强度模型和本文强度模型预测值较为接近，可用于早期粗略预测充填体强度。本文强度模型因综合考虑了充填体与围岩侧壁产生的拱架效应和后壁剪切力，曲线变化平滑且得出比较合理的充填体强度预测值，既能准确计算出小尺寸充填体的强度，又能在保证安全性和经济性的同时，更加精确地计算出大尺寸充填体自稳所需强度，适用性相对更广。将胶结充填体物理参数和采场结构参数带入上述5种充填体强度力学模型中，结果见表2.

表2 5种充填体力学模型强度预测值表

结合卧虎山矿的开采情况，一步矿房胶结充填体采用灰砂比12.5%(1∶8)，充填体强度为2.5 MPa，远大于本文强度模型计算预测值，为了验证摩擦充填体强度可以满足安全性的要求，在试验矿房采用充填体强度为85.5 kPa的充填体进行充填。充填后回采矿柱，发现充填体揭露过程中仍保持稳定，未出现垮塌现象，证明该强度可以保证充填体自立，未出现垮塌，说明本文强度力学模型是可靠的。

4 结 论

1)在一、二步矿房交替上升式充填采矿法中，根据胶结充填体与围岩之间的相互作用，考虑单侧暴露下胶结充填体的拱架效应和与后壁围岩剪切力的影响，建立了符合现场实际且适用范围更广的单侧暴露的充填体三维强度模型。

2)经过计算分析发现，考虑拱架效应和后壁剪切力的充填体强度受充填体结构参数影响较小，强度预测值随着充填体结构参数的增加变化平滑，增幅不明显。充填体与围岩接触面的粗糙程度和充填体内聚力极大程度影响了充填体的强度预测值和稳定性，接触面越粗糙，拱架效应和后壁剪切力越明显，本文强度模型预测值越小，反之则越大。

3)总结了4种经典充填体强度模型的适用性，本文强度模型预测值与Thomas强度模型、Terzaghi强度模型较为接近，总体上小于经典充填体强度模型，既满足了充填采矿中的安全性也降低了充填成本。