（六年级）如何探索“侧面积相同的圆柱体积”的规律

□王 清

怎样更好地探索、发现和理解“侧面积相同的圆柱体积”蕴含的规律呢？可采用如下教学环节。

一、创设情境，初悟规律

1.观察发现，感知不同圆柱的特点及决定因素

教师出示高矮不一、胖瘦不同的8 个圆柱（图略）。学生观察后，教师提问：“这些圆柱有什么不同？圆柱的胖瘦、高矮与什么有关？”引导学生总结：圆柱底面圆的半径决定胖瘦，高决定高矮。

2.画图计算，感悟影响圆柱体积大小的要素

教师提问：“高的圆柱体积一定比矮的圆柱大吗？胖的圆柱体积一定比瘦的圆柱大吗？”让学生通过画草图进行说明。

二、探索证明，深悟规律

1.卷一卷，展示“卷法”

教师出示4个面积都是36dm2的长方形或正方形（如图1）。如果把它们分别卷成圆柱，有几种卷法？让学生猜测、操作、验证。教师巡视指导，并收集典型作品。

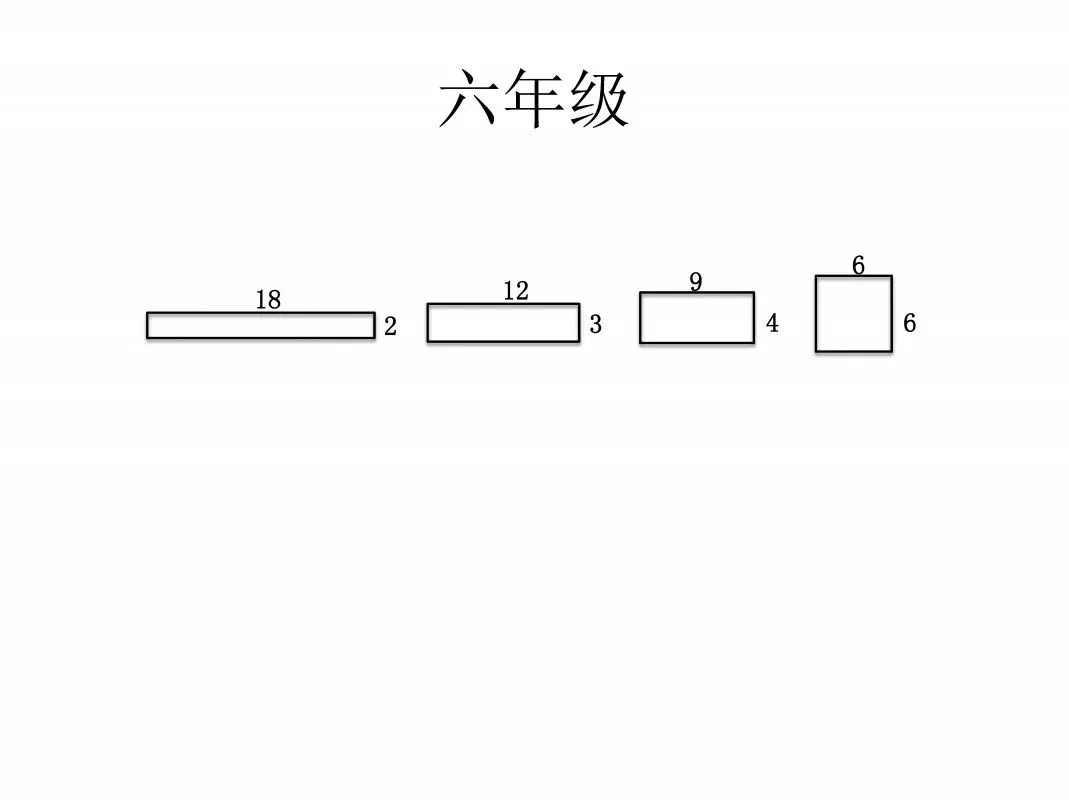
图1

2.算一算，计算“体积”

教师展示学生作品（如图2），并出示任务：想一想，一个长方形能卷出几种圆柱？长和宽分别是圆柱的什么？正方形呢？猜一猜，它们的体积谁最大，谁最小？算一算，体积分别是多少？让学生填写表1。

图2

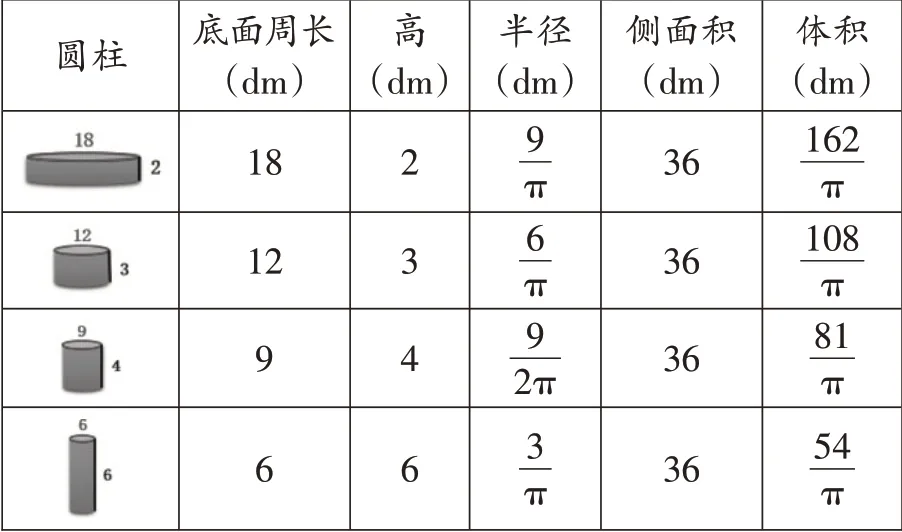
表1

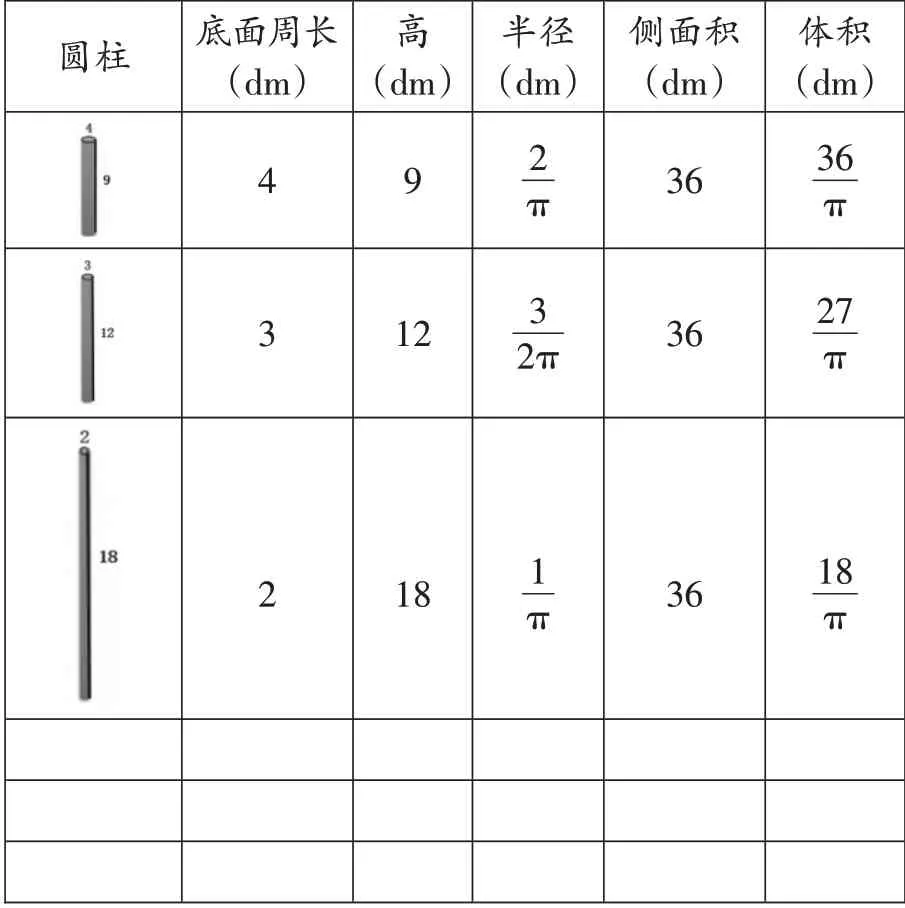
续表

3.理一理，发现“规律”

（1）让学生观察表1，思考：这些圆柱有什么相同点和不同点？总结：它们的侧面积相等，但体积不相等。

（2）让学生比较表1，思考：侧面积相同的圆柱体积有什么规律？总结归纳：侧面积相同的圆柱，底面半径或底面周长越大，体积就越大。

4.证一证，追究“原因”

（1）再次验证。请在表1空白处继续填写一些与上面不同的数据，进一步验证以上结论。

（2）证明。教师提问：“当圆柱的底面周长为ɑ，高为b 时，它的体积是多少？如果侧面积S 保持不变，圆柱体积大小与什么有关？”学生完成后，教师出示图3。

图3

通过卷一卷、算一算、理一理、证一证这些数学活动，学生不仅直观地探索发现了“侧面积相同的圆柱体积”的规律，还在探索中发展了思维能力和创新能力。