基于摩擦摆支座的轨道交通高架桥减隔震性能及设计方法研究

胡松松，陈 功，李盼到

（北京市市政工程设计研究总院有限公司，北京 100082）

1 研究背景

北京轨道交通22 号线为双线轨道桥梁，设计时速160 km/h，工程地处Ⅷ度区，地震动峰值加速度0.2 g和0.3 g。在高峰值加速度区域，以桥墩损伤为代价的延性抗震设计已不能满足结构的抗震设防标准。轨道交通要求高速平稳的安全性和舒适性，其桥梁上部梁体、下部桥墩及基础的刚度都很大，刚度大、基频高、低矮的桥墩较多是城市轨道桥梁的显著特征[1]，因其具备较小的自振周期，理论上更适合采用减、隔震技术。其中，基于摩擦摆减隔震支座的减隔震技术，已在国外桥梁的抗震设计及抗震加固中得到了广泛的应用[2-5]。

城市轨道交通桥梁大部分为30、25 m 常用跨度简支梁桥(以下简称“标准梁”)。在跨越重要相交道路、河道及其他重要构筑物时，多采用较大跨度混凝土连续箱梁桥(以下简称“节点桥”)。许多学者对轨道交通桥梁基于摩擦摆支座的减、隔震效应进行了研究，但对减隔震设计方法的适用性、经济性研究很少。目前，减隔震设计方法及技术的研究多对标准梁[6-7]或节点桥[8]单独进行分析，很少对这两种桥梁结构相邻时地震响应的相对运动关系进行研究；这方面的研究也多停留在通过采取不同的支座参数进行大量试算来减小两者的相对位移，对伸缩缝长度的设定并无便捷、规律性的设计方法。

笔者通过对北京轨道交通22 号线桥梁地震峰值加速度0.2g 区域和0.3g 区域，延性抗震设计和减隔震设计的对比研究，得出减隔震设计的适用条件；通过对标准梁和节点桥震动特性研究，得出伸缩缝装置位移控制的设计方法，为类似工程的设计提供参考。

2 减隔震支座特点

减隔震的本质就是通过各种高阻尼装置或者材料减小地震的作用，并利用较小的支座刚度将桥梁结构和引起破坏的地震作用隔离开来[9]。目前较为成熟且应用比较广泛的减隔震装置，主要有铅芯橡胶支座、高阻尼橡胶支座、弹塑性钢支座、摩擦摆减隔震支座等[10-11]。

轨道交通高速平稳的安全性、舒适性和巨大的列车活载，对桥梁支座的耐久性、初始刚度有严格要求。铅芯橡胶支座、高阻尼支座难以满足要求；弹塑性钢支座虽然具备良好的减隔震作用，但其震后不能自复位；摩擦摆支座承载能力强，耐久性及稳定性好，震后可自复位，同时具备抗平扭能力，更加适用于轨道交通桥梁。

本研究采用摩擦摆减隔震支座及双线性滞回模型进行桥梁地震动响应分析，支座采取的本构模型如图1所示。

图1 支座水平向非线性双折线本构模型 Figure 1 Horizontal nonlinear double broken line constitutive model of support

3 减隔震分析模型

3.1 有限元模型

本研究采用Midas Civil2019 有限元程序，建立多跨一联的标准梁桥空间梁单元模型。摩擦摆减隔震支座采用一般连接中的滞后系统进行模拟，通过设置非线性弹性支撑的弹性刚度、屈服强度及屈服后刚度与弹性刚度之比、屈服指数及滞后循环参数，实现支座的双折线本构关系(见图2～4)。每片标准梁下设4 个双向摩擦摆支座，节点桥边中墩各设2 个双向摩擦摆支座；桩-土相互作用采用节点弹性支撑约束，其顺桥向、横桥向及竖向刚度采用m 法计算。桩顶以下hm=2(d+1)深度范围内的土层为粉质黏土，比例系数m=10 000 kN/m4，计算地震力时，深度y 处桩基侧面水平地基系数C=2my。

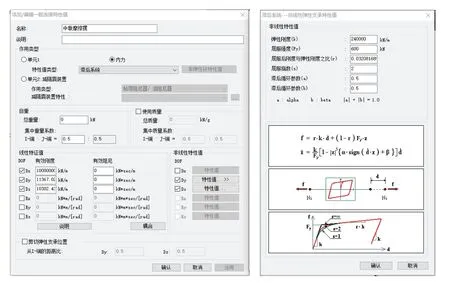
图2 支座一般连接 Figure 2 General connection example of a bearing

3.2 下部结构尺寸

以满足墩顶纵向线刚度和桥墩横向线刚度的要求为下部结构尺寸的控制原则，其标准梁不同墩高对应的下部结构尺寸如表1 所示。

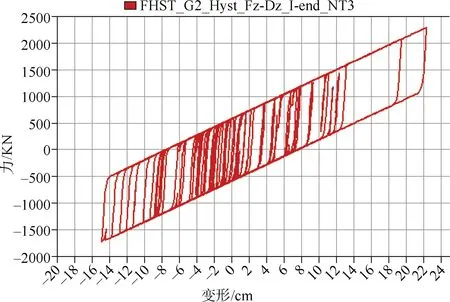
图3 支座滞回曲线 Figure 3 Hysteresis curve of a bearing

图4 标准梁有限元模型 Figure 4 Standard beam finite element model diagram

表1 不同墩高对应下部结构一览 Table 1 List of substructures corresponding to different pier heights

4 减隔震设计方法

为进一步研究轨道桥梁减隔震设计方法在高、低地震动峰值加速度区域的适用性，对比分析不同区域的减隔震设计的隔震率；针对不同的峰值加速度区域，对减隔震设计及延性抗震设计的经济适用性进行对比分析。

4.1 隔振率对比分析

本节分别对0.2g、0.3g 峰值加速度区域、不同墩高的隔震率进行对比分析，其隔震率计算结果如图5～6 所示。

由图整体观察10～25 m 墩柱高度范围内标准梁桥的减隔震率变化趋势，0.3g 峰值加速度区域的墩柱隔震率与0.2g 区域的相比并无优势，两者隔震率几乎持平；墩柱整体隔震率均维持在50%～70%之间；不同区域虽隔震率相差不大，但高峰值加速度区域初始地震能量更大，采用延性设计难度更大，采用减隔震设计更具优势。

图5 纵向隔震率计算结果 Figure 5 Longitudinal isolation rate calculation results

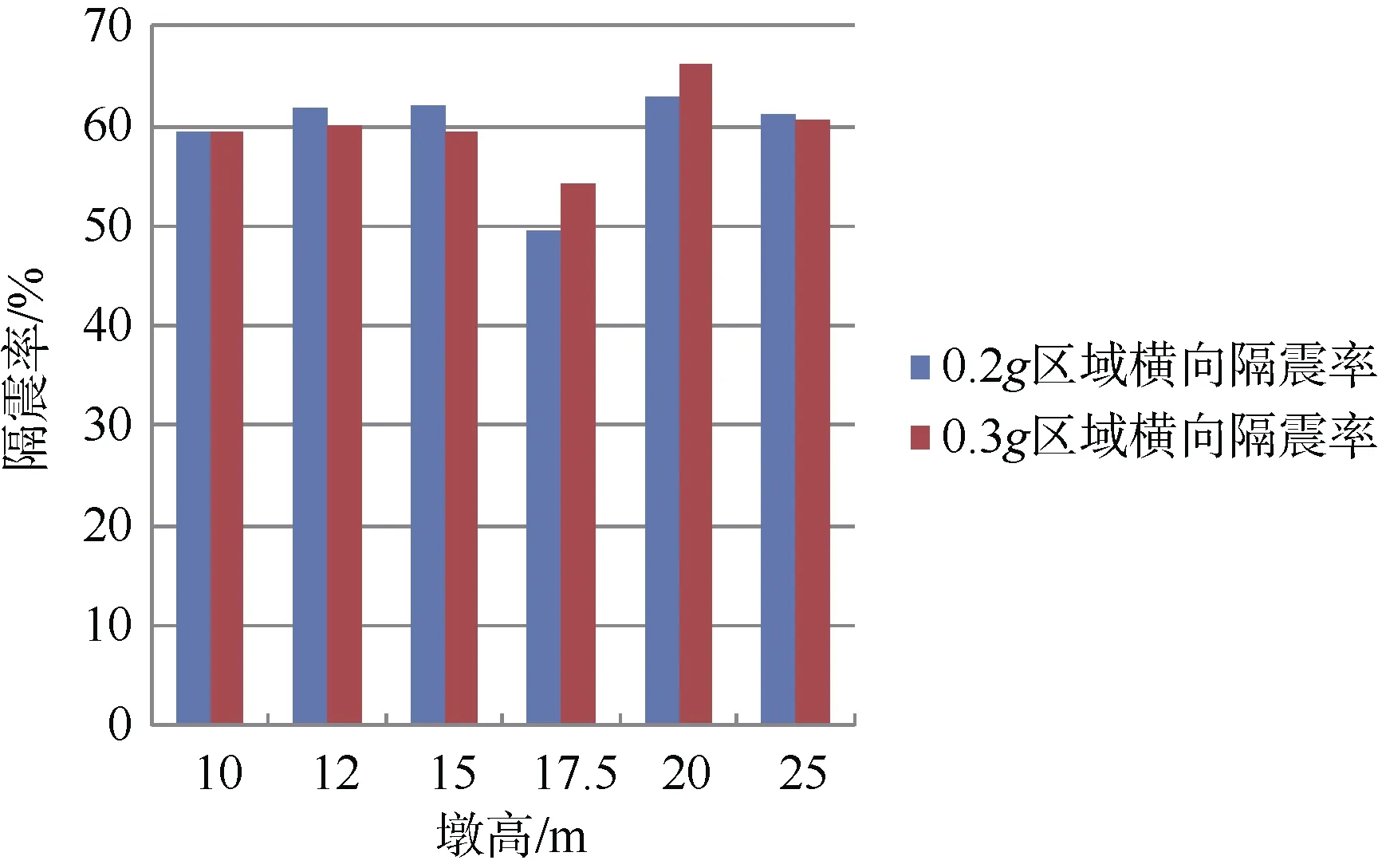
图6 横向隔震率计算结果 Figure 6 Calculation results of the lateral isolation rate

4.2 经济适用性对比

在经济性对比分析时，0.2 和0.3g 峰值加速度区域下部结构采用相同的截面尺寸。依据不同的抗震设计方法，得到下部结构的配筋及桩长计算结果，结合材料单价及球形支座与摩擦摆减隔震支座的价格差，得到单轴的下部结构的经济效益计算结果(见图7)。

图7 减隔震设计单轴经济效益计算结果 Figure 7 Calculation results of single-axis economic benefits of a seismic isolation design

由图7 可知：在高峰值加速度区域，减隔震设计相对于延性抗震设计能够大幅降低桩基长度和下部结构的配筋率，从而取得显著的经济效益，单轴下部结构能节省投资21 万～39 万元；0.2 g 加速度区域受下部结构的刚度控制，减隔震设计在一定程度上可降低配筋率，对桩基长度没有影响，仅在高墩位置取得较小的经济效益，墩高小于17.5 m 时，减隔震设计的经济效益较差。

综上分析，减隔震设计在高峰值加速度区域具备良好的经济性及较高的隔震率，该设计方法更加适用于高峰值加速度区域。

5 桥梁震动的特性

当前基于摩擦摆减隔震支座的减隔震设计研究，多停留在单独分析不同减隔震支座的隔震周期对结构响应的影响，普遍的结论也是增大减隔震支座的隔震周期能够提高结构的隔震效率。此研究方法和结论单独强调了摩擦摆支座的隔震周期，却忽略了结构自身的刚度对地震响应的影响。

在外部输入的地震能量不变的情况下，结构的地震响应是由结构的自振周期以及摩擦摆支座屈服后的摆动周期共同决定的。本研究定义减隔震结构的体系周期为T，它与结构的自振周期T1和减隔震支座的隔震周期T2相关。

为寻找两者的相关性，把桥梁结构简化成单自由度震动体系，结构的自振周期T1对应的墩柱刚度为K1，减隔震支座隔震周期T2对应的支座刚度为K2。桥梁墩柱与减隔震支座的集成刚度为K，由，从而得到结构的体系周期。体系周期与结构自振周期之比越大，结构的震动周期延长的效果越好，结构的隔震率越高；标准梁与节点桥这两种结构自振周期相差较大，通过设置不同的支座隔震周期，使两者的体系周期接近，从而减小两者的相位差和梁端相对位移。

6 伸缩缝位移控制

桥梁结构是三维的空间结构物，在各种荷载作用下会产生不同方向的变位。对于轨道桥梁来说，每跨标准梁桥间及节点桥与标准梁桥间均采用伸缩装置连接。采用减隔震设计时，由于不同跨间动力特性的差异，往往在地震来临时相邻跨的振动相位不同步，导致梁端相撞或拉开距离过大将伸缩装置拉裂。因此，在减隔震设计时，考虑影响梁端相对位移大小的决定性因素十分必要。

不同跨间的相位差，是由于二者的动力特性差异所导致的。根据前述结论，若想使这样的差异缩小，最有效的方法是通过设置不同的滑动曲面半径，实现不同的支座隔震周期，让不同跨的体系周期趋于一致。

6.1 标准梁间伸缩缝位移控制

轨道交通22 号线标准梁桥相邻跨梁端节点纵向相对位移时程曲线，如图8 所示。

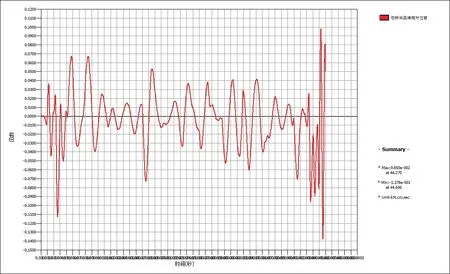
图8 梁端相邻节点相对位移时程曲线(PGA=0.3g) Figure 8 Relative displacement time history of adjacent nodes at the beam end

可以看出，轨道桥梁本身墩柱刚度较大，不同墩高时结构的自振周期差异较小，而标准梁桥均采用相同的支座减隔震周期，所以相邻跨主梁的体系周期十分接近，相位差很小，也就使梁端顺桥向位移值较小。

6.2 标准梁与节点桥间伸缩缝位移控制

就节点桥与标准梁桥相接处而言，二者的动力特性差异较标准梁间的要大，若仍采用相同的减隔震周期，则梁端相对位移会超过预设值。

下面针对墩高10 m 的标准梁与大跨混凝土变截面连续箱梁进行分析(见图9、10)。标准梁上部采用30 m 跨U 型梁，墩高10 m；节点桥采用35+50+35=120 m混凝土变截面连续箱梁，单箱双室布置，主梁部分梁高1.8～3 m；节点桥中墩采用墩顶带扩头的独柱矩形墩柱，截面尺寸2.7 m×2.5 m，墩柱高度7 m；分联墩也采用墩顶带扩头的独柱矩形墩柱，截面尺寸2.7 m× 2.5 m，墩柱高度9 m。节点桥前后各取3 跨标准梁进行验算。

图9 桥梁立面图 Figure 9 Bridge elevat

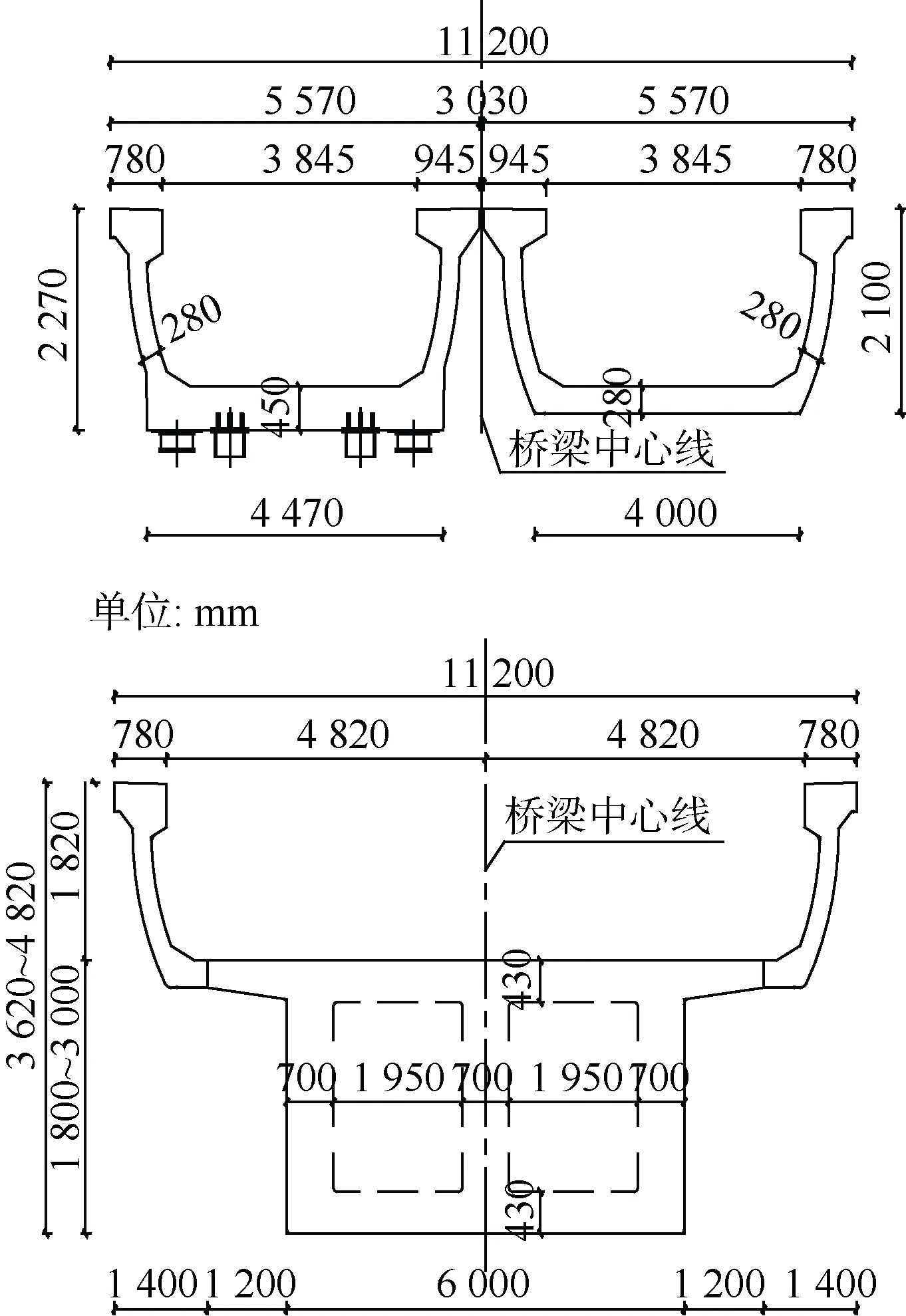
图10 桥梁断面图 Figure 10 Bridge section view

标准梁与节点桥支座隔震周期分别取1.5、2、2.5、3、3.5 s，对应支座曲率半径分别为0.56、0.99、1.55、2.24、3.04 m；U 梁支座竖向反力为1 500 kN，节点桥边墩支座竖向反力为4 500 kN，节点桥中墩支座竖向反力为15 000 kN；支座滑动摩擦系数取0.03，静摩擦系数取0.04。支座隔震周期与体系隔震周期如表2 所示。

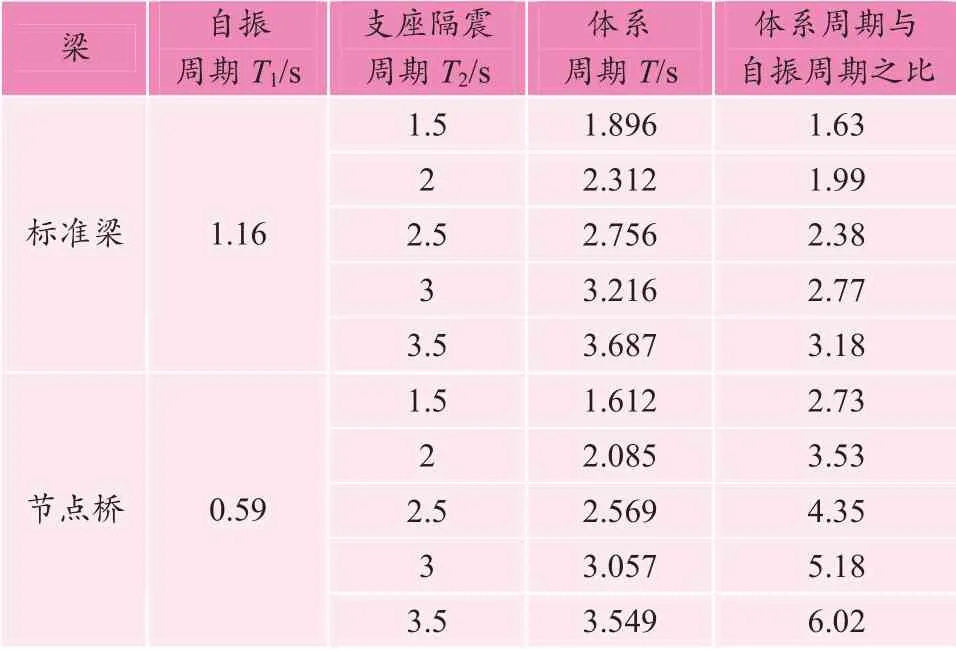
表2 支座周期及体系周期 Table 2 Periods of bearings and the system

不同隔震周期对应的标准梁与节点桥梁端相对位移计算结果如图11 所示。

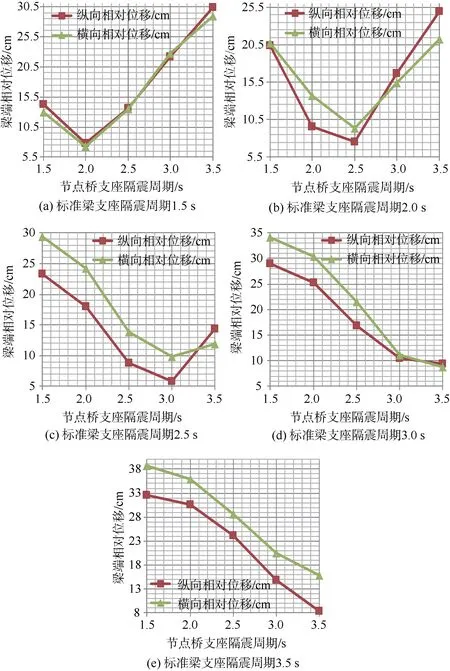
图11 梁端相对位移 Figure 11 Relative displacement of beam ends

上述计算可知：标准梁与节点桥计算方向体系隔震周期相差越小，梁端相对位移越小；通过设置合理的体系隔震周期，可以将两者的相对位移控制在小于10 cm 的较小范围内。

7 结语

笔者针对北京市轨道交通平谷线高架桥，选取典型的桥梁型式，探讨了在不同的地震峰值加速度区域减隔震设计的隔震效果，以及相对于延性抗震设计的经济优势，并在此基础上提出了梁端伸缩缝宽度的设计计算方法。

1) 0.2 g、0.3 g 峰值加速度区域，墩柱隔震率几乎持平。

2) 0.3 g 高峰值加速度区域，采用减隔震设计方法，能够取得良好的经济效益。

3) 墩柱的隔震率、梁端相对位移取决于体系隔震周期，通过设置合理的体系隔震周期，可以取得良好的隔震率、较低的梁端相对位移。

4) 标准梁和节点桥的体系隔震周期越接近，梁端相对位移越小。

在本算例中，先通过合理地设置摩擦摆支座的隔震周期，使体系周期大于结构自振周期，从而达到减隔震的目的；当体系周期为自振周期的2 倍以上时，可获得良好的隔震率。另外，使标准梁和节点桥的体系周期保持接近，降低梁端的相对位移，为梁缝宽度和伸缩缝的设置创造条件，避免梁端相互碰撞。目前，该研究成果已经应用于北京城市轨道交通平谷线的抗震设计当中，亦可为我国类似的轨道交通高架桥工程提供参考。