基于BP 人工神经网络的深基坑围护结构水平位移预测研究

2022-06-28蒙国往刘家粱黄劲松

都市快轨交通 2022年3期

蒙国往，刘家粱，黄劲松，吴波，欧强

（1. 广西大学土木建筑工程学院，南宁 530004；2. 广西大学工程防灾与结构安全教育部重点实验室，南宁 530004；3. 东华理工大学土木与建筑工程学院，南昌 330013；4. 广州城建职业学院建筑工程学院，广州 510925；5. 重庆大学土木工程学院，重庆 400045）

1 研究背景

在深基坑工程中，围护结构的水平位移是衡量基坑是否处于安全状态的重要指标之一，因此及时且准确地测量围护结构变形并预测其变形趋势，对于深基坑工程的安全施工显得尤为重要。人工神经网络普遍应用于工程中的分类汇总[1]、预测分析等方面，尤其在分析施工安全管理方面应用广泛[2-3]。胡启晨等基于Matlab 神经网络工具箱函数，建立BP(back propagation)人工神经网络预测模型，对武汉地铁车站深基坑开挖过程中围护结构水平位移进行预测，结果与实测数据基本一致，表明BP 人工神经网络应用于深基坑围护结构水平位移预测是可行和可靠的[4]。李思慧等利用人工神经网络改进的新算法最小支持向量机，建立非线性基坑变形预测模型，在实际工程中加以应用，得到的人工神经网络的预测效果具备较高的可信度[5]。由此可见，用人工神经网络对围护结构水平位移进行预测是可行的。人工神经网络算法很多，而BP 算法是应用最为广泛和成熟的[6]，所以笔者亦采用BP 人工神经网络，结合自动化监测数据，对围护结构水平位移进行预测分析。

本研究结合围护结构水平位移的自动化监测设备，在获取大量监测数据的同时，对这些数据进行BP人工神经网络的学习训练，所提出的BP 人工神经网络具有双隐层结构，且其中的神经元达到48～56 个，具有良好的预测效果和鲁棒性。根据实测数据，提出以3 种情况检测模型预测效果，结果表明神经网络预测精确度容易受其自身参数影响；采用连续不间断预测，其精确度高于间断预测；多步滚动预测的精确度可满足要求，证实了采用自动化检测设备实现自动预测的可行性。

2 基本原理

2.1 自动化监测技术

近年来，自动化监测技术在城市轨道交通中开始广泛应用。在长沙地铁5 号线万家丽广场站，成功应用AutoMos 自动化监测系统，对地铁车站基坑施工进行自动化监测[7]；在天津、兰州等地的地铁建设中，也都应用了自动化监测技术[8-9]。经市场调研，目前针对围护结构变形监测的测斜仪有多种，应用于自动化监测且技术较为先进的是某测控科技有限公司生产的HC-QX500 阵列式柔性测斜仪，如图1 所示。

图1 HC-QX500 阵列式柔性测斜仪 Figure 1 HC-QX500 array flexible inclinometer

HC-QX500 阵列式柔性测斜仪可以实现监测数据的直接读取，也可以通过无线采集终端自动采集数据，再传输到远程终端浏览，如图2 所示。现在，施工监测技术已经达到相当高的自动化程度，可以自动收集和储存数据；但收集到的数据应该如何进行挖掘，使其能指导实际施工，将其价值最大化，是目前自动化监测技术急需解决的问题。而用之前的监测数据去预测监测目标之后的变化趋势，则是自动化监测的热点之一，也是笔者研究的重点。

2.2 BP 人工神经网络

人工神经网络的学习算法可分为三类：一是有导师学习，二是无导师学习，三是灌输式学习。本研究根据实际情况，以围护结构水平位移的真实监测数据为样本基础，进行连续和间隔1、2、4 天不同时间步长划分，采用有导师的学习。划分不同时间步长的目的是：分析样本数量不同对预测值会有什么影响；比较4 种情况下哪种预测值更准确。也就是说，

图2 监测数据传输 Figure 2 Schematic of a data transmission monitoring system

输入数据为前一天的真实监测数据，输出数据为后一天围护结构水平位移的预测值，对比围护结构水平位移的真实监测数据，根据预测值与真实监测数据的误差结果进行权值调整，直至调整到预定误差范围内或预定学习次数而终止学习，并认为该BP人工神经网络已达到学习目的，可将其用于监测数据的预测。

本研究采用BP 算法进行学习，如图3 所示，输入向量X=(x1, x2, …, xi, …, xn)T，图中x0= -1 是为隐藏层神经元引入阈值而设置的；隐藏层输出向量为Y=(y1, y2, …, yj, …, ym)T，其中y0= -1 是为输出层神经元引入阈值而设置的；输出层输出向量O=(o1, o2, …, ok, …, ol)T，期望输出向量为d=(d1, d2, …, dk, …, dl)T，输入层到隐藏层之间的权值矩阵为V=(V1, V2, …, Vj, …, Vm)T，其中列向量Vj为隐藏层第j 个神经元对应的权向量；隐藏层到输出层之间的权值矩阵为W=(W1, W2, …, Wk, …, Wl)T，其中列向量Wk为输出层第k 个神经元对应的权向量。由于BP 人工神经网络已普遍应用于各行各业[10-13]，故具体推导不再赘述。

3 实现流程

3.1 参数选取

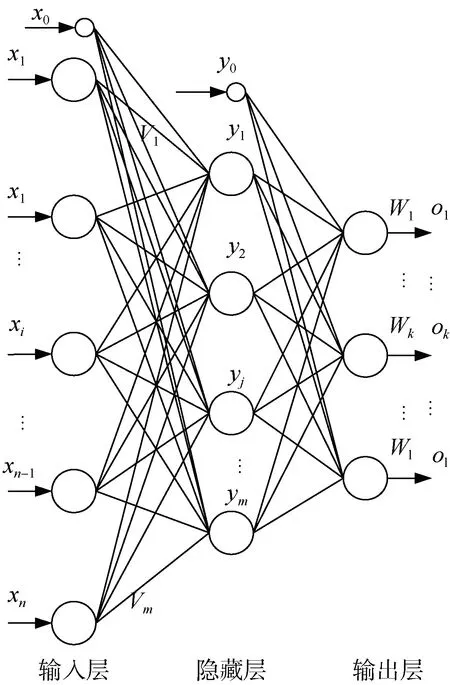
图3 层次型网络结构 Figure 3 Hierarchical network structure

BP 人工神经网络需要对样本进行学习，样本的数据作为输入端，需要对数据进行归一化或者标准化处理，将样本数据限制在区间[0，1]或 [-1，1]内。由于围护结构水平位移变化量以向基坑内偏移为正，向基坑外偏移为负，故本研究采用f(x) (∈-1，1)的Sigmoid双极性变换函数，可减少对输入输出数据处理的工作量；由于围护结构水平位移变化曲线为非常复杂的非线性曲线，其变化规律涉及原因众多，虽然BP 人工神经网络隐含层的层数越多，预测分析能力的效果越好，但同时会大大增加计算量。Kolmogorov 理论指出，双隐层结构能解决任何复杂的分类问题，而该结论已经过严格的数学证明[6]。基于此考虑，本研究采用双隐层网络结构进行BP 人工神经网络的构造，包含输入层、两层隐含层、输出层共4 层，输入层节点数为围护结构水平位移随深度变化间隔0.5 m 取一个监测值的个数。同理，输出层亦是如此。隐层节点数参照经验公式计算，有

式中，m 为隐藏层节点数，n 为输入层节点数，l 为输出节点数，α 为1～10 之间的常数。

由于学习方式有现场的真实监测数据，故采用有导师学习方式，权值更新采用BP 算法，即误差反向传播算法；引入Resilient(有弹性的)更新值概念，直接修改权值大小，相比于附加动量法和自适应学习速率法，弹性BP 算法(RPRPOP)的收敛速度更快。在案例分析中，其他参数针对实际情况进行选择。

3.2 具体步骤

本研究旨在利用自动化监测设备获取监测数据，采用BP 人工神经网络进行学习，实现围护结构水平位移的变形预测目标，并基于此实现提前预警功能，具体流程如图4 所示。

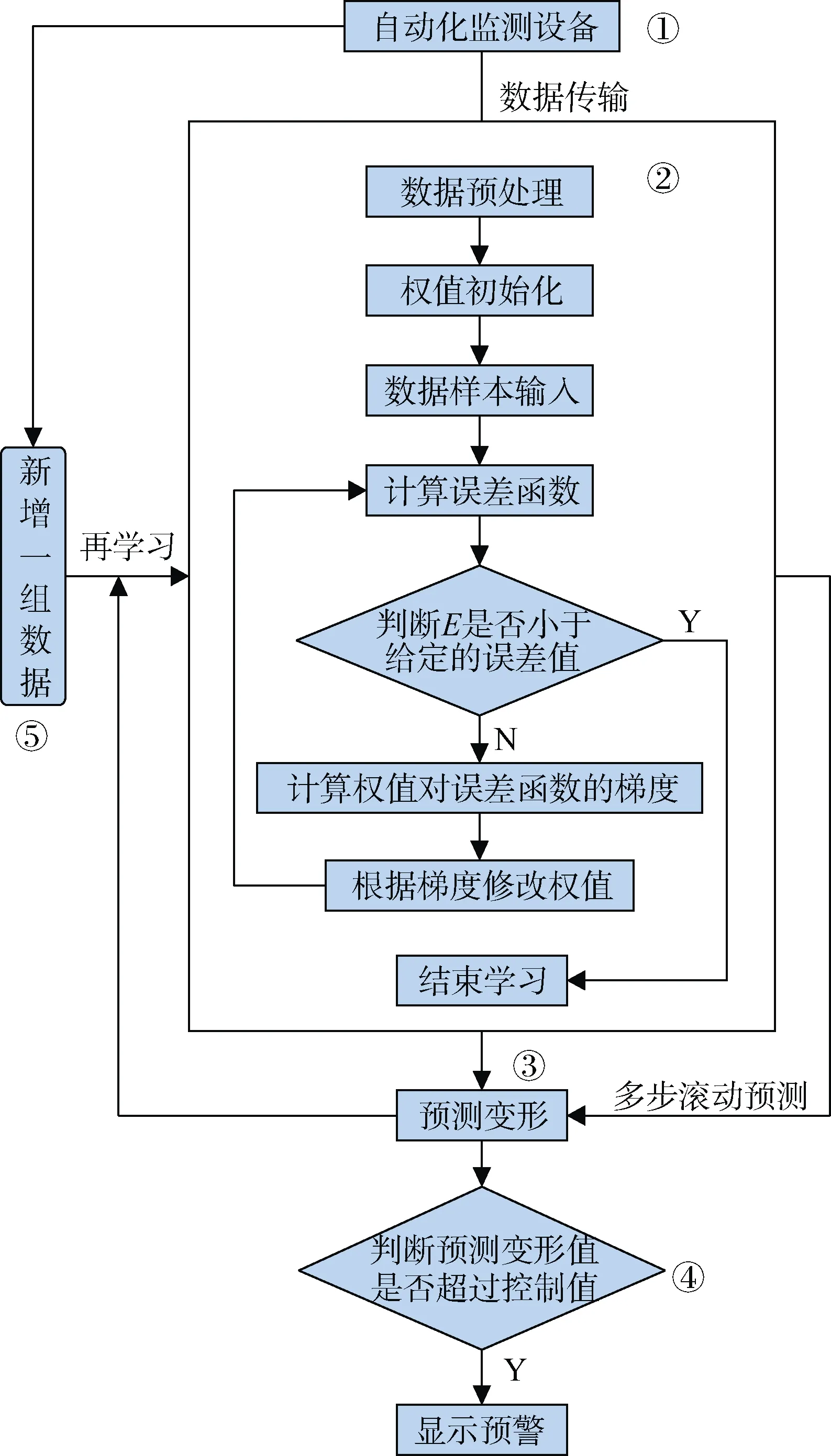
图4 BP 人工神经网络自动预测流程 Figure 4 Automatic prediction of an artificial neural network

1) 从自动化监测设备上获取围护结构水平位移监测数据，作为BP 人工神经网络的学习样本。

2) 在学习之前，需要对数据进行预处理和权值初始化，预处理主要是解决各输入和输出变量尺度不统一的问题，通过尺度变换处理，将网络的输入、输出数据限制在[0，1]或[-1，1]区间内。如某输入变量在0～1×105范围变化，而另一输入变量在0～1×10-5范围变化，这时需进行尺度变换，使所有变量都在0～1或-1～1 之间变化，从而使网络训练在一开始就给各输入变量以同等重要的地位。本研究BP 网络的神经元均采用Sigmoid 变换函数，变换后可防止因净输入的绝对值过大而使神经元输出饱和，继而使权值调整进入误差曲面的平坦区。一般预处理可根据如下常用公式进行，有

式中，xi为输入或输出数据，xmin为数据变化的最小值，xmax为数据变化的最大值，xmid为数据变化范围的中间值。

其中，式(2)是将输入、输出数据变换为[0，1]区间，式(3)将输入、输出数据变换为[-1，1]。

本研究采用迈实BP 人工神经网络软件，可自动实现该步骤功能；设有n 天的监测数据，采用第1 天到第n-1 天的数据作为样本输入，用第2 天到第n 天的数据作为BP 人工神经网络的输出预期值，让BP人工神经网络进行学习。

3) 学习完成后，用第n 天的数据作为样本输入，以此来预测第n+1 天的监测数据。这里需要说明的是，因针对每根桩都设置一个BP 人工神经网络进行不同的数据样本学习，故对BP 人工神经网络的泛化能力不做过多的要求，相对注重于其拟合能力，因此未设置测试样本对学习结果进行检验。

4) 预测值与提前设置好的监测控制值进行比较，根据比较结果，可发布不同预警信息或不预警。

5) 重复前面4 个步骤的内容，输入新的实测数据进行新的学习训练，用第n+1 天的真实数据去预测第n+2 天的监测数据，再判断是否预警。如此类推循环，实现多步滚动预测[14-15]。

4 实例分析

4.1 工程概况

下面以南宁市降桥站基坑开挖为例进行分析，该站采用明挖法施工。对施工工期进行了详细的时间统计和工期节点的划分，如表1 所示。

表1 施工时间节点 Table 1 Due dates of construction

续表

4.2 数据点选择

针对该基坑在开挖过程中围护结构水平位移的实际变形情况，选取了5 根在开挖过程中都出现过预警的围护桩来进行预测分析。如图5 所示，桩号从ZQT16～ZQT20(每根桩长为26.5、27.5、27.5、27.5、29.5 m)，位于基坑东侧扩大端处，基坑从东向西开始开挖。由于东侧存在偏压情况以及开挖过程中存在钢支撑架设滞后等现象，导致周边围护结构水平位移出现预警。围护结构水平位移从2018 年9 月21 日开始用传统测斜仪监测到2019 年4 月30 日结束，监测数据从2018年10 月24 日开始陆续出现预警直至监测结束。

图5 围护桩测点平面示意 Figure 5 Plan of the measuring points of a retaining pile

4.3 学习训练

本研究采用迈实BP 人工神经网络软件进行计算，具体参数如表2 所示，其他参数均保持默认。由于每根桩埋深不同，各桩的BP 人工神经网络在输入层和输出层的节点数上有所区别。例如，ZQT16 埋深为26.5 m，桩每隔0.5 m 有一个监测点，即对应一个监测数据，则从0～26.5 m 就存在55 个监测点，故输入层的神经元个数就为55 个，相应输出层的神经元个数也为55 个，其他桩以此类推。隐含层的神经元个数根据式(1)采用试凑法[6]，即α 分别从0 取到10 进行尝试，最终发现隐含层1的神经元数取12时模型的鲁棒性最好，收敛最快，故隐含层1 的神经元数取12，隐含层2 的神经元数在单独测试中α 取0～10 的任何整数时，对预测结果差距甚微，故从减小计算量考虑，取α=0，这时根据式(1)，隐含层2 的神经元数取10。函数类型在前面的参数选择中有说明，在此不再赘述。学习速率无固定取值，范围在0～1 即可，但笔者在多篇参考文献中发现学习速率均取0.5 以下，故本研究参照金晶的相关论文[16]，并在软件中验证，最终学习速率取0.15。同时，在BP 人工神经网络训练过程中发现，选择误差精度为10-5和训练次数1 000 次时训练效果最好，且训练时间也控制在1 min 之内，足够满足施工中实时预测的要求。对样本数据分别进行3 种模式学习：第一种，每根桩学习后在同一时间的预测结果与其实测值作对比；第二种，同一根桩在不同时间间隔样本学习后在同一时间的预测结果与其实测值作对比；第三种，同一根桩在实现多步滚动预测后对预测结果与其实测值作对比。

表2 BP 人工神经网络参数选择表(ZQT16) Table 2 Artificial neural network parameter selection (ZQT16)

4.4 预测分析

在训练中，选取3 个在施工过程中具有代表性的时间节点，对围护结构水平位移进行预测，模式1 为出现预警现象的第3 天；模式2 为基坑开挖见底的时间节点；模式3 为主体结构底板完成后的时间节点，预测结果如表3～5 所示(因篇幅限制，只列出桩体10～15 m 深度范围的水平位移)，显示了每个模式下围护结构水平位移的真实值和经过学习训练后得出的预测值，通过对比分析可得到一些结论。

模式1 的学习训练从开始监测到2018 年10 月27日，共26 个样本数据，用28 日监测数据预测29 日的监测数据。5 根桩的围护结构水平位移预测值与真实值的误差较小，误差在5%以内的节点数约占60%，误差在10%以内的节点数占80%；最大误差为3.22 mm，最小误差0.01 mm。图6 展示了桩ZQT16 和ZQT20预测结果的拟合程度，ZQT16 是5 根桩中拟合效果最不理想的，分析其原因可能是由于训练次数过少导致。ZQT16 在训练次数为5 000 时的拟合程度比训练次数为1 000 时的拟合效果要好很多，但为了统一对比，5 根桩均采用训练次数为1 000 的训练模式，而其余4 根桩都如ZQT20 一样，可得到较为理想的拟合效果，总体上满足施工监测误差的要求。

模式2 的学习训练到2018 年11 月11 日，用12 日的监测数据预测13 日的监测数据。由于训练间隔时间不同，导致学习样本的数量不同，因此预测结果存在差异。预测结果拟合程度最好的是连续不间隔天数预测和间隔4 天预测，误差在5%以内的节点数约占74%；最差的则为间隔2 天的预测值，误差为5%

表3 模式1 的学习训练结果(10～15 m) Table 3 Results of learning and training in mode 1 (10～15 m) mm

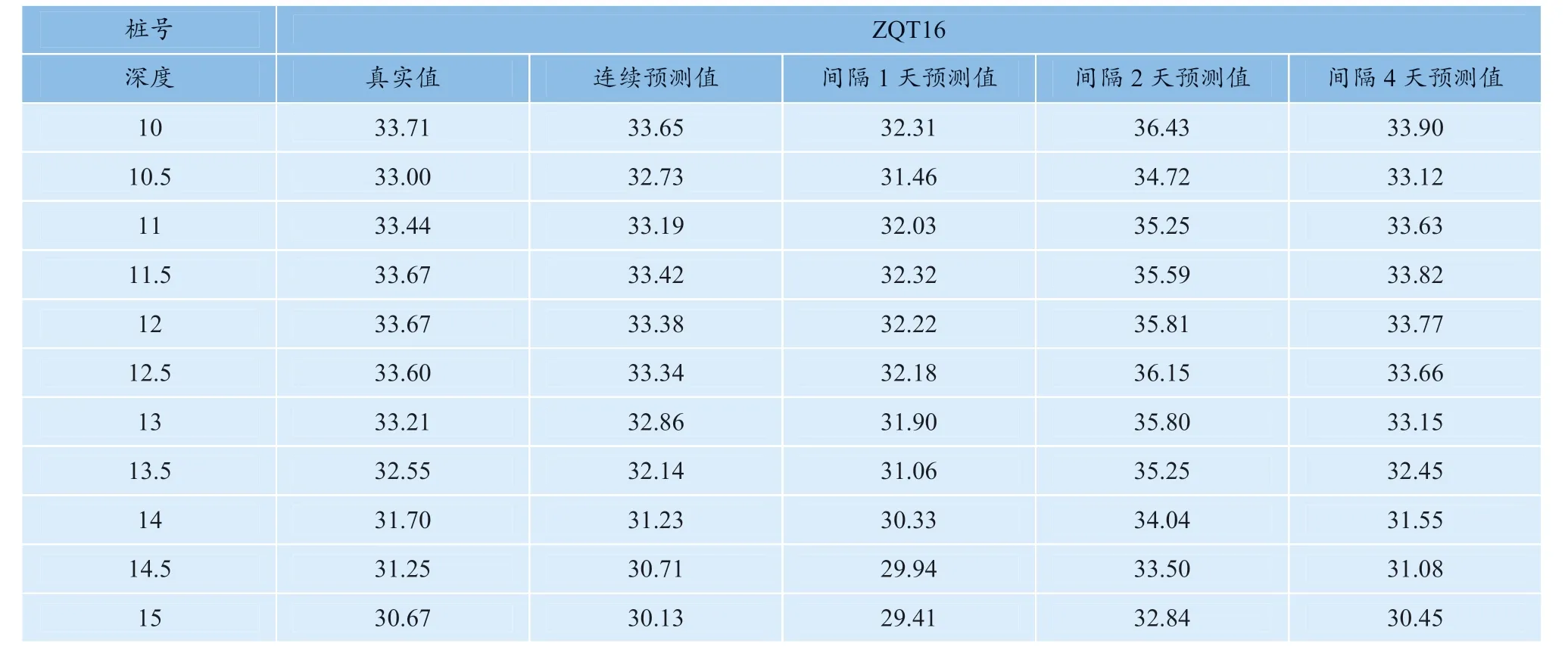
表4 模式2 的学习训练结果(10～15 m) Table 4 Results of learning and training in mode 2 (10～15 m) mm

表5 模式3 的学习训练结果(10～15 m) Table 5 Results of learning and training in mode 3 (10～15m) mm

图6 模式1 预测结果对比 Figure 6 Comparison of prediction results of model 1

以内的节点数仅占2%，但误差在10%以内的可达到64%；最小误差均可达到0.01 mm，最大误差为间隔2 天的预测值，达到2.7 mm。图7 所示为间隔1 天和间隔2 天的预测结果，拟合程度较其他两种类型存在一定差距，这也从侧面说明样本数量对BP 人工神经网络鲁棒性存在影响。本研究连续不间隔天数学习样本为41 个，间隔4 天的样本数量过少，易存在预测结果不稳定的情况，故建议样本数量不低于40 个。

图7 模式2 预测结果对比 Figure 7 Comparison of prediction results of model 2

模式3 的学习训练到2018 年12 月6 日，而后用每天获取到的真实监测数据加入到原来的样本中重新进行学习，用于预测后一天的监测数据。依此循环6天进行滚动学习，直至用11 日的监测数据预测12 日的监测数据作为结束，模拟多步滚动的预测效果。6 天的预测值误差在5%以内的节点数占比都大于62%，其中12 月7 日、8 日、10 日、12 日可达到90%，预测效果较好，12 月9 日、11 日预测效果稍差。分析原因是：样本数量会对神经网络预测效果产生影响，但总体而言误差在0.5 mm 以内的节点数占比小于50%，6 天的预测误差在5%以内的节点占比达86%，表明可达到较好的预测效果。因此，在样本数量趋于稳定且逐步增加的情况下，BP 人工神经网络体现出较好的鲁棒性和预测效果，说明多步滚动预测存在可行性，可信度也较高。