地铁杂散电流动态分布特性分析
2022-07-11沈超董志伟
沈超 董志伟
(1.中铁电气化局集团西安电气化工程有限公司 陕西省西安市 710038)2.西安工程大学电子信息学院 陕西省西安市 710048)
随着轨道交通的不断发展,方便快捷是大多数人选择地铁作为出行的必备选择,地铁不仅会带给人们方便,也会带来了一些负面影响。由于地铁利用走行轨兼做回流轨,对于运行多年的地铁线路来说,在列车运行时会发生杂散电流的泄露。杂散电流会对地铁本体以及地铁沿线的埋地金属、燃气管道、以及钢筋混凝土建筑造成腐蚀。研究杂散电流泄漏的规律,针对杂散电流的泄漏规律提出防范措施,对于杂散电流的治理有重大的意义。
目前对于杂散电流的分布研究主要有静态分布模型和动态分布模型,大量学者对于杂散电流的分布规律已经开展了一系列的研究。文献建立杂散电流电阻网络静态分布模型,并对影响杂散电流分布的重要因素进行仿真分析。文献采用分布式电路模型对于某站的钢轨电位和杂散电流进行了数值模拟,并将模拟的数值与现场试验进行比较,确定了其方案的正确性。文献建立基于电场的杂散电流分布模型,求出埋地金属受到的腐蚀量。文献研究了轨道交通中不同的接地策略对于杂散电流的影响,并给出两站之间的模拟结果。文献搭建了基于单注入源和多注入源的两层、三层、四层地下杂散电流仿真分布模型。文献建立多列车不同工况下的杂散电流分布情况,分析各个参数对杂散电流的影响。文献提出了一个拓扑模型,用于评估直流牵引供电系统中明挖区间的动态杂散电流。文献研究了列车不同运行时刻对杂散电流和轨道电压的影响,得出加速和减速时杂散电流较大。文献在MATLAB/SIMULINK 环境下对电动列车的模型进行仿真,比较了不同土壤类型中的杂散电流量。文献基于城市轨道交通杂散电流的形成机理和危害,利用CDEGS 软件建立轨道交通牵引供电模型。详细介绍了杂散电流在地铁中的分布。文献首先推导单点注入时的杂散电流分布模型,然后将单独的点利用叠加原理相加得出整条线路上的杂散电流分布模型。文献将列车的牵引特性加入回流系统,建立地铁杂散电流动态分布模型,分析在地铁列车运动变化的情况下杂散电流的分布情况。文献搭建地铁牵引回流系统的暂态模型,然后在列车动态运行的情况下进行仿真,分析列车运行过程中轨道电位的分布情况。
上述对于杂散电流的分布研究大多数采用静态分布模型,但实际地铁的运行是一个动态变化的过程。基于列车运行的动态过程和电阻网络模型,建立了轨道交通杂散电流的动态分布模型。通过分析不同影响因素对杂散电流分布的影响,得出杂散电流动态分布的情况。
1 杂散电流的腐蚀危害
1.1 杂散电流腐蚀的原理
地铁列车牵引供电系统为直流供电,列车通过钢轨进行回流。由于钢轨较长加之隧道环境复杂,无法完全与大地绝缘,一部分电流泄漏到大地,地铁杂散电流形成及腐蚀原理见图1。在泄露点的位置钢轨作为电化学反应的阳极区,埋地金属作为电化学反应的阴极区,在此点杂散电流将会腐蚀钢轨及其附件。在变电所附近变电所为阴极区,此时位于变电所附近的埋地金属为电化学反应的阳极区,杂散电流对埋地金属造成腐蚀污染。
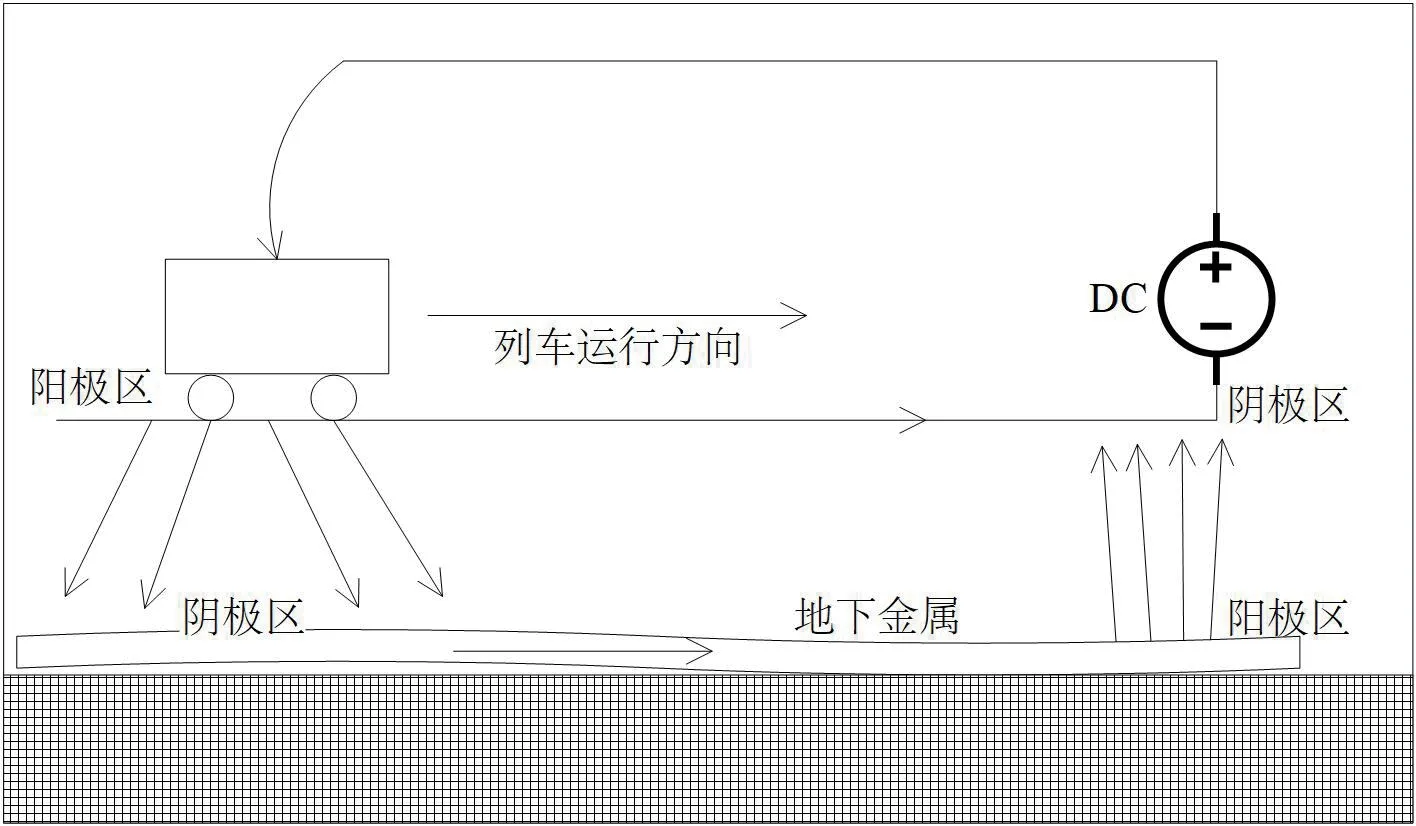
图1:地铁杂散电流形成及腐蚀原理示意图
1.2 杂散电流腐蚀的危害
由图1 可知,在电流的泄露的位置处于阳极区,根据电化学反应此处的金属会发生污染腐蚀。有调查表明,杂散电流泄漏严重的地方要频繁更换轨道。当电流从泄露位置流向大地后,会在变电所处回到牵引变电站的负极,此时牵引变电站附近的金属为阳极并发生污染腐蚀。杂散电流对于埋在地下的管道也会产生电化学腐蚀。有调查发现位于地铁沿线附近的埋地管道存在腐蚀,污染严重的地方管道几年内会发生点蚀,所以杂散电流的治理问题变得十分重要。
2 杂散电流动态分布模型
2.1 电阻网络模型
杂散电流动态模型是根据电阻网络模型加上列车动态特性组成的,杂散电流电阻网络模型主要有:轨道和大地双层模型、轨道、排流网和大地三层模型、轨道、排流网、管道和大地四层模型,其中轨道、金属网、管道和大地组成的四层电阻网络模型更加符合实际情况。
在建立静态分布模型的过程中假设:
(1)轨道纵向电阻分布均匀;
(2)轨道对排流网之间的过渡电阻分布均匀;
(3)排流网纵向电阻分布均匀;
(4)排流网对埋地金属之间的过渡电阻分布均匀;
(5)接触网阻抗忽略不计。
轨道、金属网、管道和大地四层模型见图2,如图所示:R为钢轨纵向电阻;g为钢轨和排流网之间的过渡电阻;R为排流网纵向电阻;g为排流网-埋地金属过渡电阻;R为埋地金属纵向电阻;g为埋地金属-大地过渡电阻。
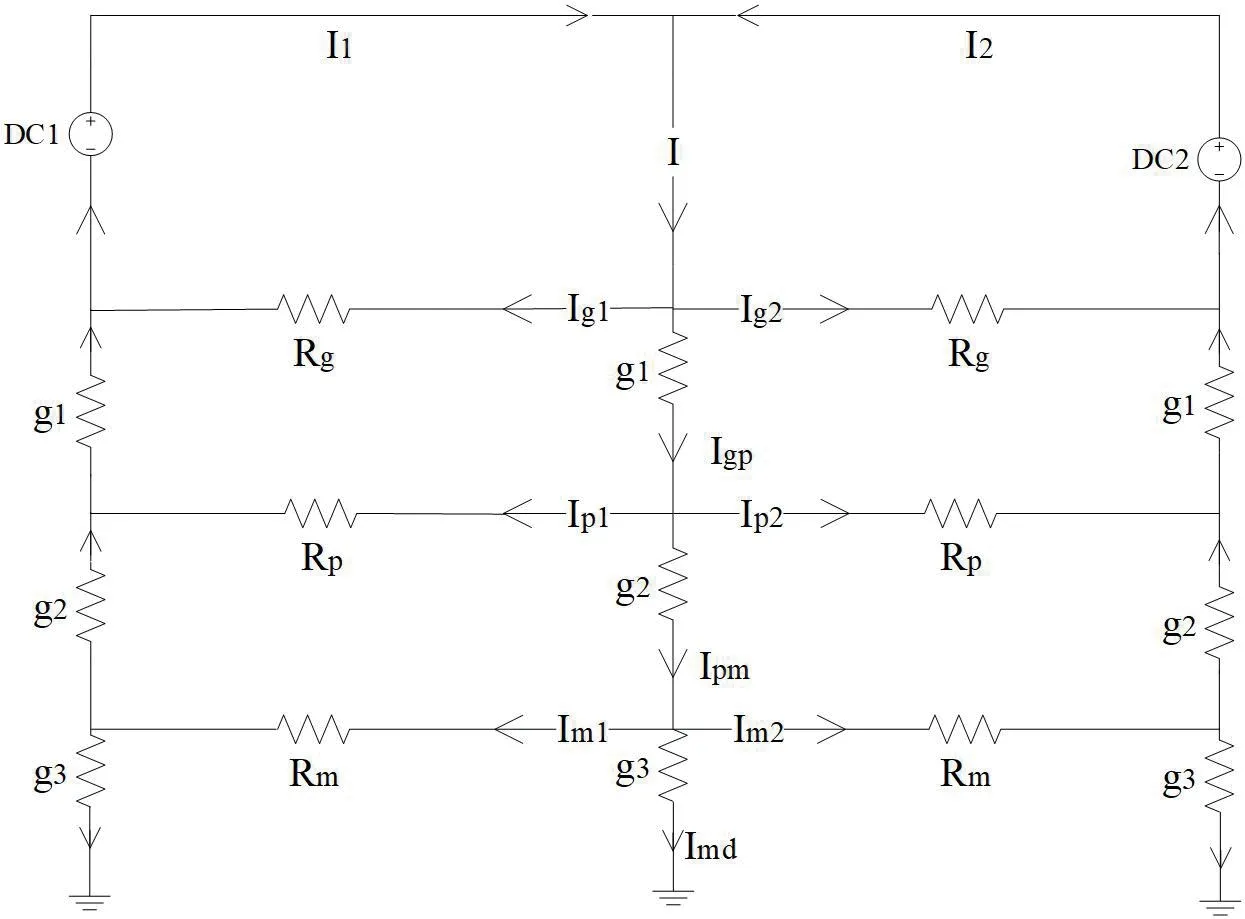
图2:钢轨-排流网-埋地金属-大地四层电阻网络模型
双边供电模式下,I和I为来自两个牵引变电站的牵引电流;I 为列车某一个位置的取流;I和 I为轨道电流;I为钢轨-排流网电流;I和I为排流网电流;I为排流网-埋地金属电流;I和I为埋地金属电流;I为埋地金属-大地电流。
2.2 杂散电流动态模型
将列车看成一个不断移动的质点,在进行列车牵引计算时,各个参数的取值如下:两站的距离为1.5km;列车总质量为300t;列车启动加速度为1m/s,制动加速度为1.2m/s;牵引网电压为1500V;列车的最大运行速度为80km/h;
根据速度与时间的公式:v=v+a;位移与时间的公式:L=vt+1/2a;
经过计算可得到:列车的速度-时间曲线见图3、位移-时间曲线见图4、列车取流-时间曲线见图5;由图3 可知,列车加速运行至22.3 秒后进入匀速运行阶段,经过46.82秒后进入制动减速阶段。由图4 可知,列车首先加速行驶248.6m,然后匀速行驶1044.4m,最后减速行驶207m。由图5 可知列车在加速启动阶段和制动减速阶段列车取流大小与时间成正比关系。当列车速度最大时,此刻列车取流最大。列车开始进入制动减速阶段时,此刻列车取流最小可达-5351A。
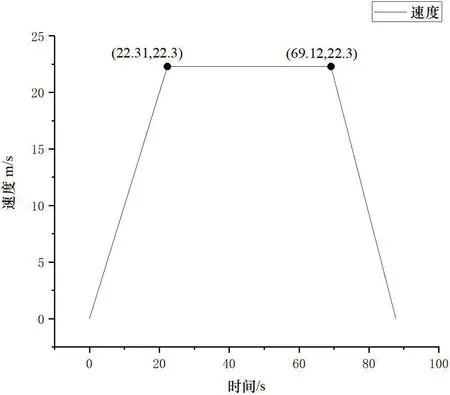
图3:速度-时间曲线

图4:位移-时间曲线
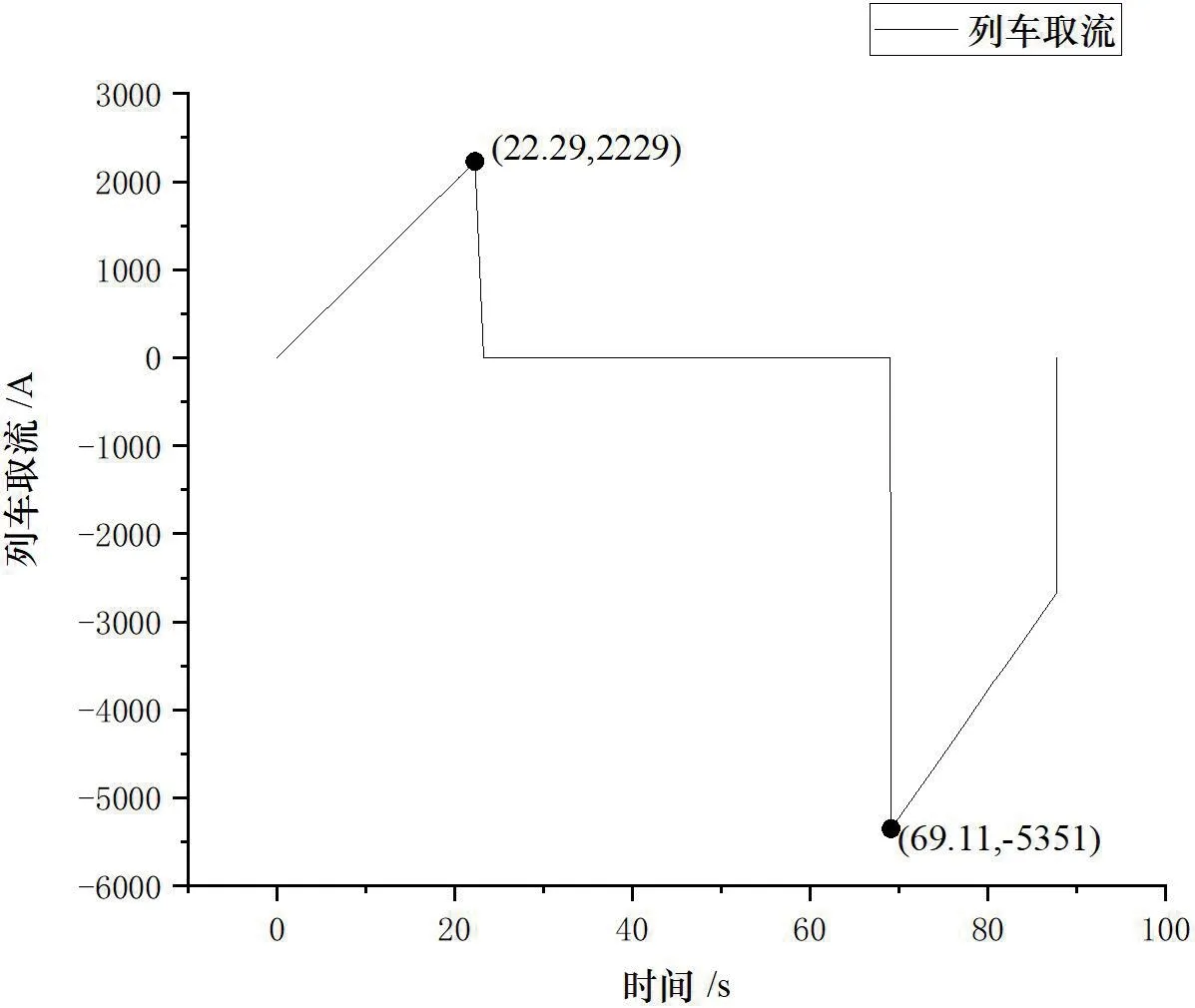
图5:列车取流-时间曲线
本文在电阻网络模型的基础上加入列车的动态变化,从而建立杂散电流动态分布模型。由图3、4、5 可知,在不同的运行工况下列车速度、位置、取流都是不断变化的,根据这些变化规律在静态电阻网络分布模型上分析杂散电流的动态分布规律。
3 杂散电流动态分布仿真分析
3.1 动态建模
将1.5km 的地铁线分成若干个小段,每一小段都由四层电阻网络模型组成,根据取流、位置关系建立杂散电流动态分布模型,列车取流-位置曲线见图6。由图6 可知,列车在248.4m 处正向取流达到最大的2229A,此后列车将进行1044.6m 的匀速直线运动,在做匀速运动区间列车的取流很小接近于0。当列车运行到1293m 处时,列车将进入制动减速阶段,此时列车反向取流达到最大的-5351A,直到列车进站停稳列车取流为0,然后进入下一个运动区间。
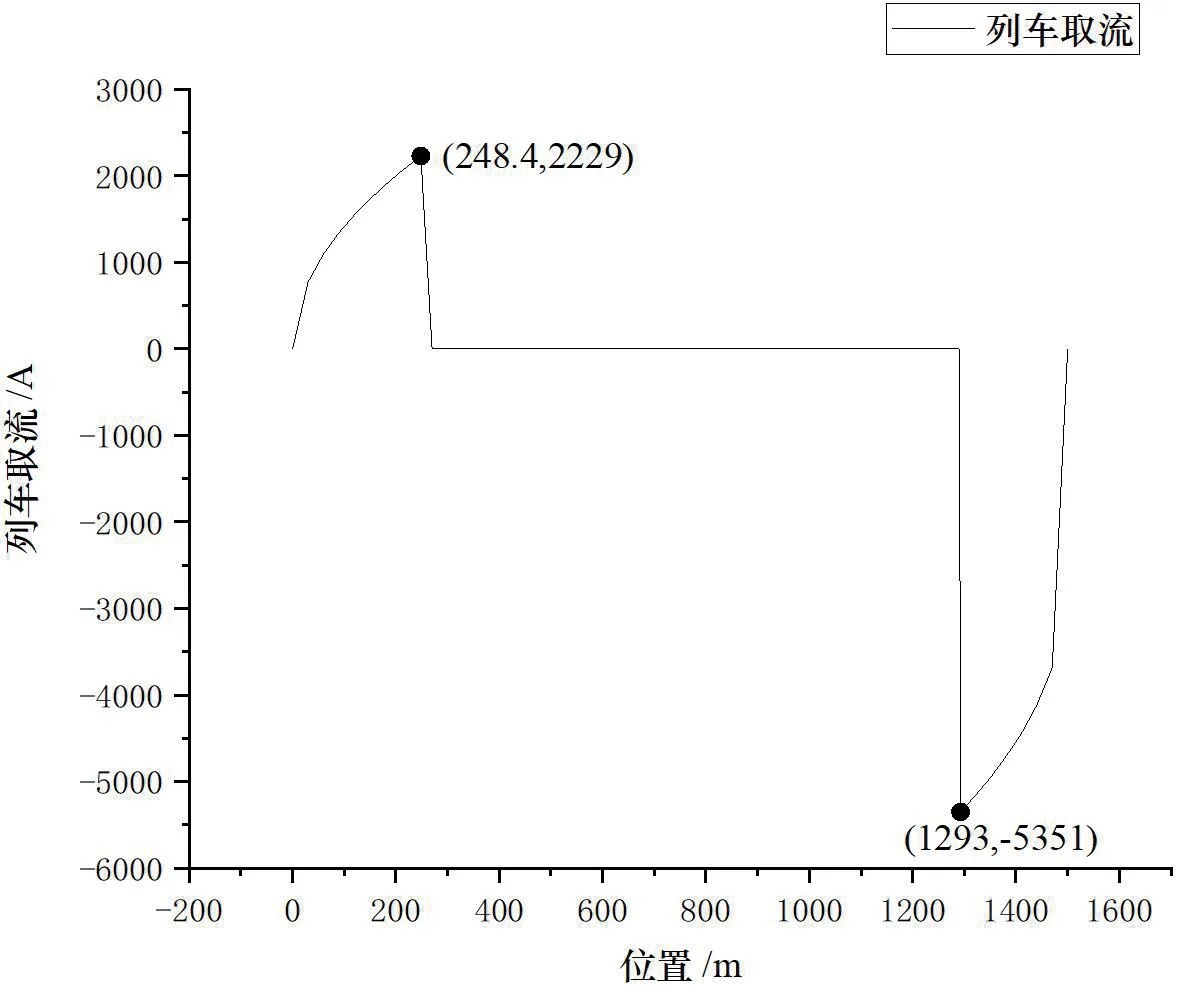
图6:列车取流-位置曲线
3.2 静态仿真分析
假设全线过渡电阻分布均匀,列车位置固定,只改变列车的取流大小。对于列车在同一位置进行不同取流的情况进行仿真,建立全线杂散电流分布曲线见图7(a)。由图可知列车取流越大,该点的杂散电流就越大,整条线路上的杂散电流泄露较为严重。列车取流固定,只改变列车的位置。对于列车在不同位置位置进行相同取流的情况进行仿真,建立全线杂散电流分布曲线见图图7(b)。由图可知列车在位于变电站中间的位置电流泄露较大,离变电所越近电流泄露越小。改变240m 处的轨道排流网过渡电阻,列车取流和位置固定,对于列车在过渡电阻不均匀的情况下进行仿真,建立杂散电流分布曲线见图图7(c)。由图可知杂散电流的大小随着过渡电阻的变化而变化,过渡电阻越小泄露的电流越大。
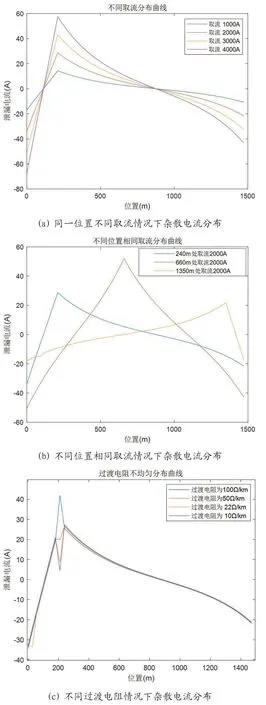
图7:杂散电流静态分布曲线
3.3 动态仿真分析
以上静态仿真结果与文献中的静态数学模型得到的结论相同,可以证明此电阻网络模型的正确性。结合静态模型和列车运动状态,建立动态仿真模型。当全线过渡电阻为均匀的15Ω/km 时,根据图7 中列车位置取流曲线,不断改变列车的位置和取流,对列车不同位置、不同取流的情况进行仿真分析,建立杂散电流动态分布图,杂散电流动态分布见图8。由图可知在列车加速阶段和制动减速阶段杂散电流泄露最严重,在匀速运行阶段杂散电流的泄露很小。由此可知列车取流对于杂散电流的分布有很重要的影响,当列车取流越大时杂散电流就越大,取流越小杂散电流就越小。

图8:过渡电阻均匀分布时杂散电流动态分布曲线
4 结语
综上所述,本文主要研究杂散电流的动态分布特性,完成了杂散电流分布的仿真模拟实验,得到列车位置、列车取流和杂散电流大小三者之间的关系,并利用实验数据绘制杂散电流动态分布图。通过仿真试验分析了杂散电流分布的主要影响因素,结果表明,列车的位置、列车的取电流和轨道绝缘电阻是影响杂散电流分布的重要因素,并且得到机车启动加速和制动减速时产生的杂散电流泄露最大,列车匀速运行阶段产生的杂散电流最小。此结论可为杂散电流防护和治理措施做出参考。
