基于方位角和偏移距联合约束的三维超虚折射干涉法❋

余文斌， 邹志辉,2❋❋， 郭振波， 李培明

(1. 中国海洋大学海洋地球科学学院海底科学与探测技术教育部重点实验室， 山东 青岛 266100； 2. 青岛海洋科学与技术试点国家实验室 海洋矿产资源评价与探测技术功能实验室， 山东 青岛 266237； 3. 东方地球物理公司物探技术研究中心，河北 涿州 072751； 4.东方地球物理公司， 河北 涿州 072751)

在近地表地质情况复杂的地区, 低信噪比的初至折射波引起初至拾取的不准确，尤其在地质构造的复杂化和地震资料信噪比下降都会增加辨别信号的难度[1]，限制了地震速度建模的精度，如何提高初至折射波信噪比是地震勘探亟待解决的重要问题。基于地震干涉原理建立的虚折射干涉法是一种有效提高初至折射波信噪比的方法，该方法通过成对地震道的互相关叠加来重构地震记录[2]，但该方法难以确定初至的绝对时间，并且缩减了初至的偏移距范围[3]。针对该问题，Mallinson等[4]和Bharadwaj等[5]提出了超级虚拟折射干涉法，该方法基于虚折射干涉法的虚拟道概念，增加了原始地震记录与虚拟道卷积叠加的步骤，从而实现了地震道的重构。Al-Hagan等[6]提出了迭代超虚折射干涉法，能有效提升较低信噪比的初至折射波。由于以上方法无法保证远近偏移距恢复的一致性，在超虚折射干涉法基础上，乔宝平等[7]提出的逆虚折射干涉法，保证了远近偏移距叠加次数的一致性。安圣培等[8]通过子波整形压制了虚拟道中的虚假同相轴。对于互相关和卷积产生的子波旁瓣，梁上林等[9]引入了反褶积处理步骤。吕雪梅等[10]提出的相似度加权的超虚干涉法提高了压制局部异常噪声的能力。针对OBS资料台站间距较大，虚拟道叠加次数不足的问题，宋龙龙等[11]和高福建等[12]提出了基于相邻虚拟道叠加的超虚折射干涉法，使得大台站(炮点)间距、长偏移距的数据的初至波得到有效增强。然而，超虚折射干涉法是建立在二维介质情况下，理论上不适用于三维情况[13]，需要进行改进才能适用于三维数据。

Lu等[14-15]提出的常规的三维超虚折射干涉法通过沿测线的积分叠加实现三维地震数据初至波增强。然而，在实际应用中，三维数据地震道数量多，该方法需要进行大量的互相关运算，计算效率较低，而且全工区叠加可能引入大量非近似传播路径的折射波参与叠加，引起增强后地震波形的相位偏差，造成初至时刻的不准确。本文通过方位角和偏移距的约束，筛选炮点和检波点，得到具有近似重叠传播路径的折射波，逼近满足超虚折射方法的假设，实现对三维初至波增强，提高初至波增强后初至的准确度。本文利用单折射界面模型和多层模型进行理论测试，单界面模型主要测试基于方位角约束的三维超虚折射干涉法的效果，而复杂模型则用于测试仅用方位角约束的不足，基于方位角和偏移距联合约束的三维超虚折射干涉法效果，并最终将该方法应用于三维实际地震资料的初至波增强。

1 方法原理

基于方位角和偏移距联合约束的三维超虚折射干涉法主要为互相关生成虚拟道和卷积重构目标道两个部分。

1.1 互相关生成虚拟道

互相关生成虚拟道的目标是提取震源的两个检波点对之间的介质响应。基于方位角约束的三维超虚折射干涉法在三维工区中筛选炮点时，通过对如图1(a)中的检波点对连线与检波点-炮点连线之间的方位角∠SRfRn进行约束筛选炮点。当约束的方位角较小时，从炮点激发，近道检波点Rn、远道检波点Rf接收的初至折射波地震记录具有近似重叠的传播路径，因此，筛选得到的不同炮点生成虚拟道可以进行叠加，如图1(b)所示。

然而，在实际情况下，由于地下的速度介质是连续变化的，随着偏移距的增大，初至折射波的射线路径之间的差异逐渐增大，将会导致不同炮点的两检波点对之间的介质响应随偏移距的增大而存在差异。仅利用方位角约束进行虚拟叠加道时会约束不足，大偏移距范围内叠加将导致生成的叠加虚拟道不准确，从而影响初至折射增强的准确度。因此引入偏移距的约束，即通过控制叠加的偏移距段Yn，如图1(a)中所示，控制叠加的范围，使得选择叠加范围内的初至折射波有近似的传播路径，再进行虚拟道叠加，从而提高虚拟道的准确度。划分偏移距段后，检波点对Rn、Rf对于不同的偏移距范围就会生成相应的虚拟道。

((a)生成虚拟道时炮点的筛选(红色星为炮点，绿色三角为检波点)；(b)近道Rn、远道Rf的初至折射地震记录互相关生成虚拟道并叠加(*代表互相关，深黑色的虚拟道参与叠加，灰色的虚拟道方位角过大不参与叠加)。(a) Screening sources when generating virtual traces (Red star represents source, Green triangle represents receiver); (b) The first arrivals of Rn and Rf cross-correlate to generate virtual traces and stacking (*represents cross-correlation, only stacking black virtual traces).)

超虚折射干涉法中互相关生成虚拟道可以用如下公式表示[2]：

φ(S,Rn,Rf)=g(S,Rf)g(S,Rn)*。

(1)

式中：φ(S,Rn,Rf)为虚拟道；g(S,Rf)、g(S,Rn)分别表示炮点S到检波点Rf、Rn的初至折射记录在频率域表达式；*表示复共轭。

若工区中有N个炮点，通过方位角约束，可以筛选得到K个炮点。在方位角约束筛选的基础上再通过偏移距约束，筛选得到M个炮点。筛选得到的炮点激发，检波点Rn、Rf接收得到的初至折射记录互相关生成虚拟道，然后进行虚拟道叠加，表达式如下：

(2)

式中：Ф(S,Rn,Rf)为叠加生成的虚拟道；i为筛选得到的炮点号。

在互相关生成虚拟道时，常规的方法并未对炮点进行筛选，需要进行大量的互相关运算，效率较低[10]。而本文通过方位角和偏移距的约束，对满足约束条件的炮点筛选，能够有效减少在生成虚拟道时互相关的次数，从而提高了运算的效率。

1.2 卷积重构目标道

卷积重构目标道是利用参考道(高信噪比近道)和对应的虚拟道进行卷积运算以重构目标道(低信噪比远道)。基于方位角约束的三维超虚折射干涉法在重构目标道(Rf)进行筛选参考道(Ri)时，通过约束参考道和炮点、目标道之间的夹角∠RiSRf和∠RiRfS，如图2(a)所示，使得从炮点S激发，参考道和目标道的初至折射记录具有近似重叠的传播路径。然后利用筛选得到的参考道与对应的虚拟道卷积重构出目标道，并进行叠加，就可以以实现对目标道的增强，从而提高初至折射的信噪比, 如图2(b)所示。

偏移距约束重构目标道时，判断炮点S与待增强目标道的偏移距属于哪一个偏移距范围Yn，如图2(a)，选择对应偏移距段范围的参考道进行筛选，然后用筛选得到的参考道与该偏移距范围的参考道与目标道所对应的虚拟道卷积，重构出目标道并进行叠加，就可以实现对目标道的增强。

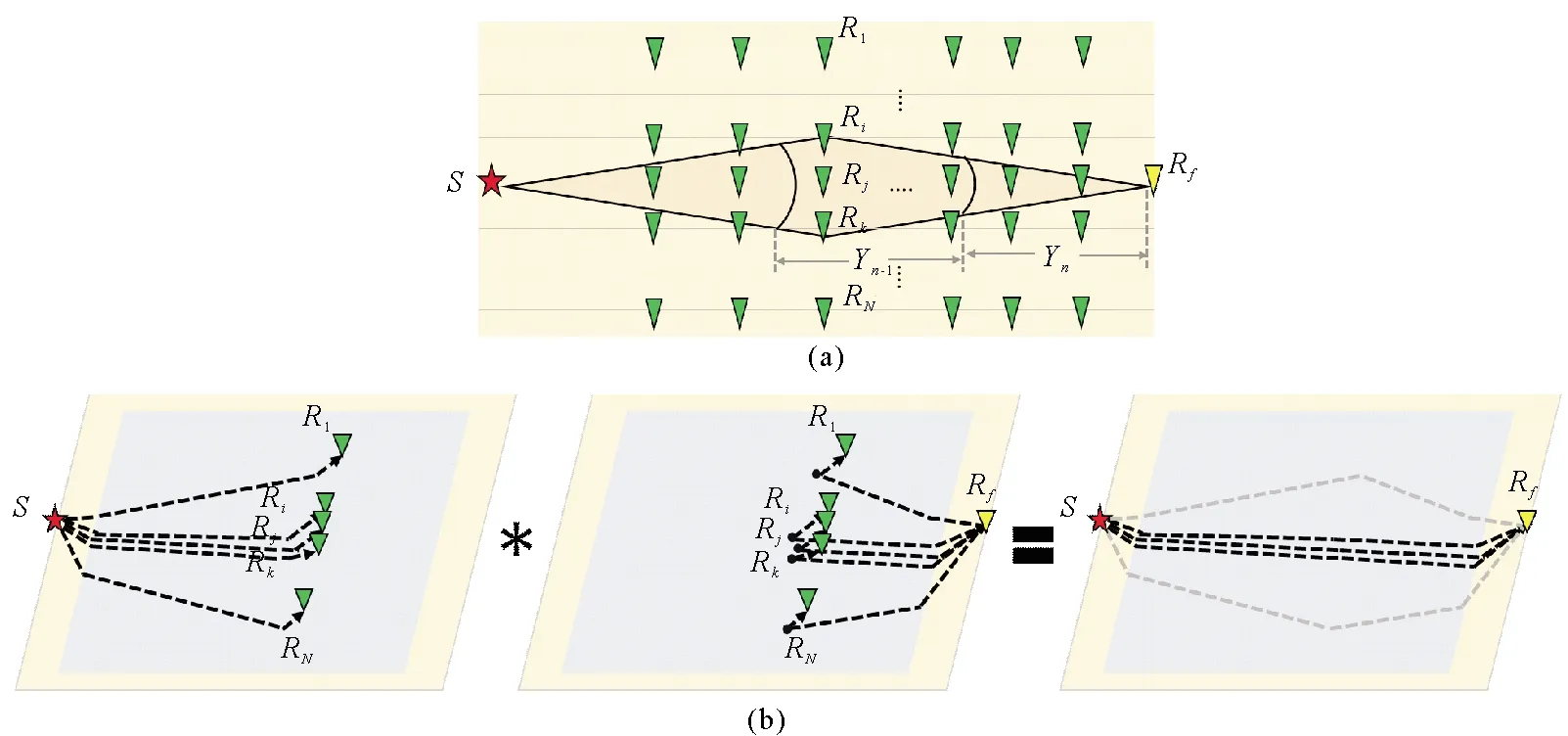
((a)参考道的筛选(红色星为炮点，绿色三角为检波点，黄色三角为目标道)；(b)参考道与相应的虚拟道卷积重构得到目标道Rf(*代表卷积，深黑色的目标道参与叠加，灰色的目标道夹角过大不参与叠加)。(a) The screening of the reference trace (Red star represents source, Green triangle represents receiver, Yellow triangle represents target trace)； (b) The reference traces convolved with the virtual trace to reconstruct the target trace Rf(*represents convolution, only stacking black target traces).)

超虚折射干涉法中卷积重构初至折射的表达式如下[4]：

g(S,Rf)super=g(S,Ri)Ф(S,Rn,Rf)。

(3)

式中：g(S,Ri)为高信噪比参考道的初至折射在频率域表达式；Ф(S,Ri,Rf)为参考道Ri和目标道Rf之间对应的虚拟道；g(S,Rf)super为重构得到的目标道。

若工区内共有N个检波点，通过如图2(a)中角度∠RiSRf和∠RiRfS约束筛选，有K道参考道。角度筛选的基础上再通过偏移距的约束，有M道参考道与虚拟道卷积来重构目标道。表达式如下：

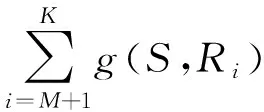
(4)

式中：G(S,Rf)为叠加重构得到的初至折射记录；i为筛选得到的参考道的道号。

在卷积重构目标道的过程中，通过方位角和偏移距的约束，对满足约束条件的参考道筛选，能够卷积的运算次数，相对于常规的方法，在保证精度的情况下进一步提高了运算的效率。

2 理论模型数据测试

为了测试本文方法对三维结构所产生初至波的增强效果，本文分别建立了单界面速度模型和多层模型。单界面模型主要测试基于方位角约束的三维超虚折射干涉法的效果，而多层模型则用于测试仅用方位角约束的不足，基于方位角和偏移距联合约束的三维超虚折射干涉法效果。并且还在文中讨论了改变子波的主频时，对于初至增强的影响。

2.1 模型1：单折射界面模型

为测试基于方位角约束的三维超虚折射干涉法，首先构建了一个倾斜双层三维速度模型，模型的大小为15 km×10 km×3 km，上层、下层速度分别为2.5和4 km/s，如图3(a)所示。观测系统如图3(b)所示，检波点间距为25 m，测线间距为250 m，在Y、X方向上，炮点间距分别为150和100 m，共有400个炮点。每一炮的接收范围大小为7.5 km×5 km，共21条测线，每条测线上有300个检波点，共6 321个检波点。正演采用伪谱法正演[16]，震源子波采用主频为20 Hz的雷克子波。对理论数据添加75%随机噪声(75%指的是添加的随机噪声的最大振幅值与b-b’测线3.75 km处的地震记录绝对值的最大振幅比)，为消除进行初至波增强时初至波形外其他波形的影响，还对数据进行了初至截取，只保留初至附近的波形记录。抽取图3(b)中a-a’、b-b’、c-c’ 三条测线地震记录，如图3(c)所示，截取的窗口的位置为图3(c)中黑色虚线所示，可以看到，加噪数据在远偏移距处初至信号变差。

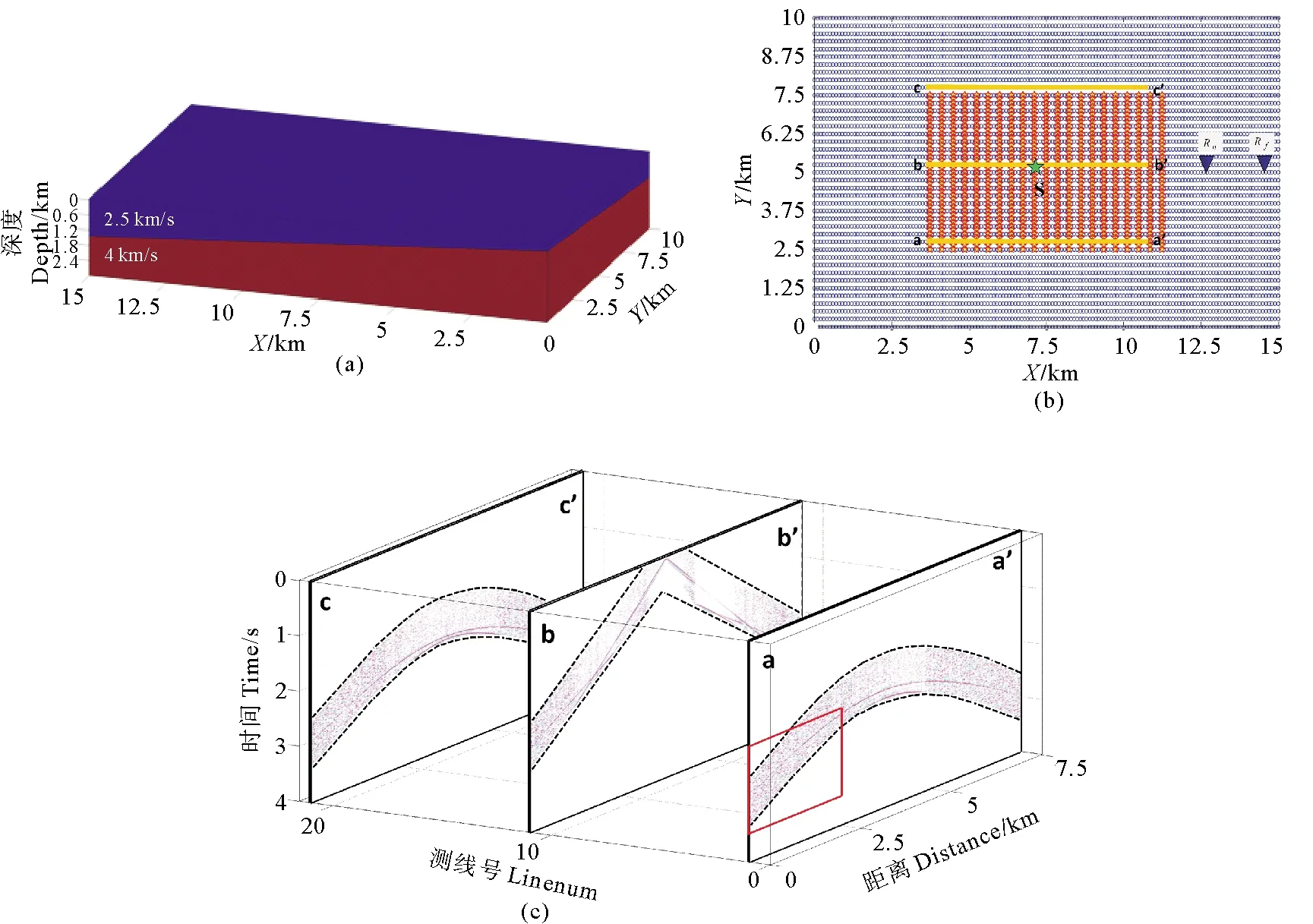
((a)速度模型；(b)观测系统(图中红色星为炮点，蓝色点为检波点；深蓝色三角代表图4中生成虚拟道的两个检波点位置；增强测试所选择的炮点和测线分别为绿色星和黄色测线)；(c)加噪后截取初至的地震记录(黑色虚线为截取初至的窗口,红色方框为局部放大显示的区域)。(a)Velocity model; (b)Geometry(Red star represents source, Blue point represents receiver; Dark Blue triangle represents the positions of the two receivers that generate the virtual trace inFig 4; The source and survey lines selected for the enhancement test are green star and yellow lines respectively); (c) Adding noise first arrival data after time windows (The black dashed line shows the boundary of the time window; The red box is the area that is zoomed.).)

为研究方位角对初至波增强的影响，选择图3(b)中所示的两检波点对Rn、Rf。将所有炮点，两检波点对Rn、Rf接收的初至折射记录互相关生成的虚拟道按照方位角∠SRfRn排列，如图4(a)所示。可以看到，随着方位角∠SRfRn的增大，不同的折射波的传播路径差异变大，互相关后得到虚拟道的峰值时刻逐渐变得不再一致。

在地层平缓的情况下，小方位角范围内虚拟道所对应的折射波路径近似在同一平面内，在选择叠加虚拟道的方位角范围时，可以选择较小的方位角范围叠加生成虚拟道的峰值时间为参考。在这里，本文选择5°方位角范围叠加得到的虚拟道作为参考的叠加虚拟道，其峰值时刻为4.120 s。分别将图4(a)中虚拟道的峰值时刻与参考的叠加虚拟道峰值时刻做差，如图4(b)所示。随着方位角的增大，时差增大，在10°范围内，时差在0.01 s以内；20°范围内，时差在0.015 s以内；在30°范围内，时差基本都小于0.02 s。

由于叠加虚拟道的方位角范围的选择将会影响叠加虚拟道峰值时刻的准确度，影响增强后初至波到时的准确度。因此，将方位角分别在10°、20°、30°范围内的虚拟道以及80°范围内虚拟道叠加，分别得到叠加虚拟道，如图4(c)所示。图4(c)的叠加虚拟道结果显示，随着叠加的方位角范围的增大，叠加虚拟道峰值时刻与5°方位角叠加道峰值时刻之间的时差逐渐增大，分别为-0.002、-0.013、-0.016和-0.018 s。增强时所选择的方位角范围内叠加虚拟道的峰值时刻与5°范围内叠加虚拟道的峰值时刻差不超过0.012 5 s，即子波主周期的四分之一(主频为20 Hz子波的主周期T为0.05 s)，因此，选择的方位角为10°。进行方位角的选择，虚拟道叠加时将能保证同相叠加，从而提高叠加虚拟道的信噪比和准确度。

还需要注意的是，为消除重构后地震道有“假同相轴”的影响，本文还对叠加虚拟道施加高斯窗口，只保留最大峰值附近的虚拟道信息，即施加高斯窗口后的叠加虚拟道类似于δ函数[8，11]。

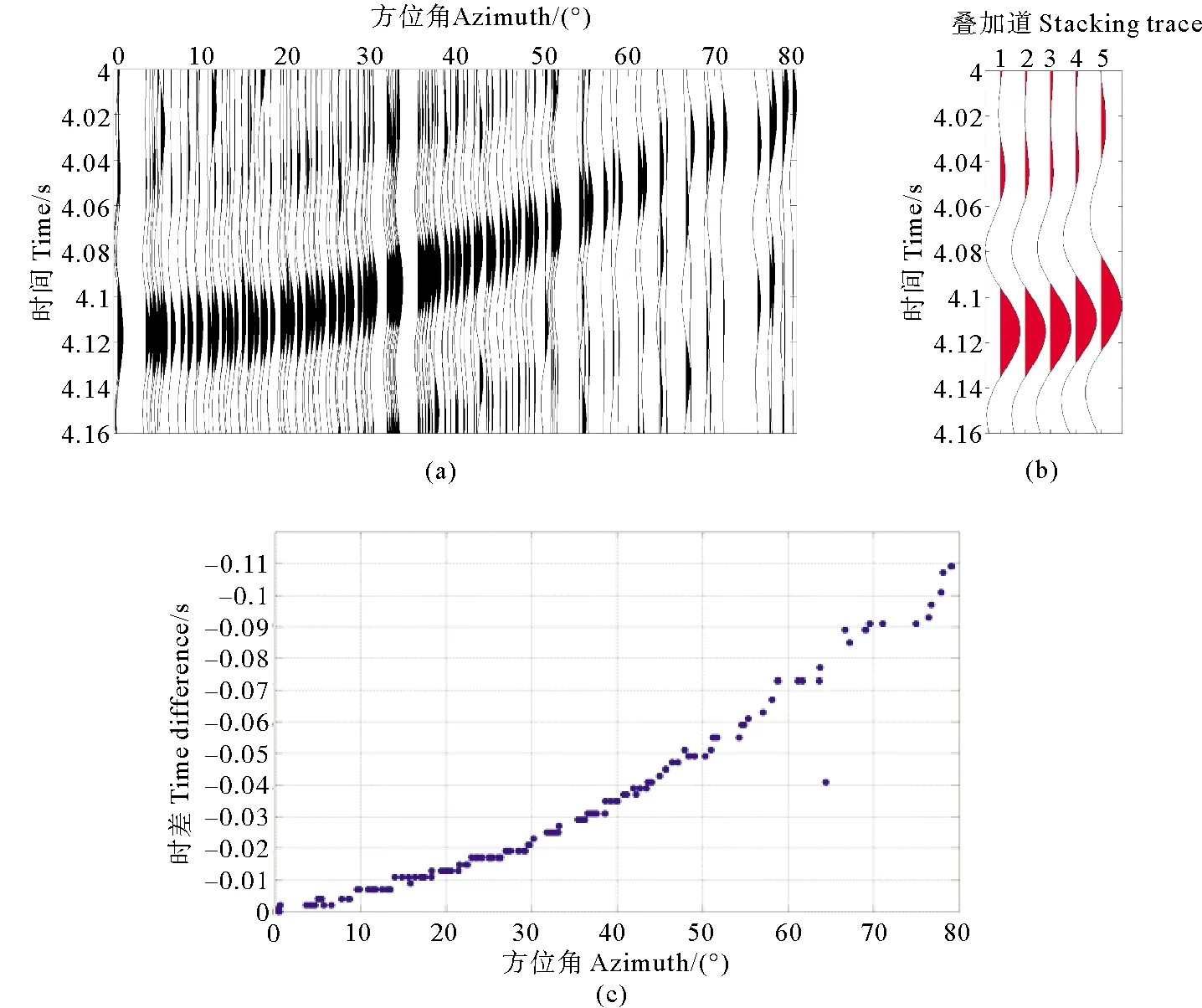
(虚拟道所对应检波点对如图3中Rn、Rf所示。(a)按方位角排列的虚拟道集；(b)虚拟道峰值时刻时差；(c)不同方位角范围的叠加虚拟道(第1、2、3、4、5道分别为方位角在5°、10°、20°、30°、80°范围内虚拟道叠加得到的叠加虚拟道)。(a) Virtual traces arranged by azimuth(The angle is the azimuth ∠SRfRn); (b) Time difference between peak times of virtual traces;(c) Stacking virtual traces with different azimuth ranges(Traces 1, 2, 3, 4 and 5 are superimposed virtual traces with azimuth of 5°, 10°, 20°, 30° and 80° respectively.).)

接下来进行了初至波增强测试，图5(b)所示地震道为图3(c)中红色方框区域局部放大，原始的理论数据如图5(a)所示。首先利用Lu等[14-15]提出的沿测线积分叠加的常规的三维超虚折射干涉法进行初至波增强，用该方法进行初至波增强得到的结果如图5(c)所示，用本文中基于方位角约束三维超虚折射干涉法初至波增强后的结果如图5(d)所示。从初至波增强前后的对比，可以看到，理论加噪数据的信噪比较低，尤其是红色虚线圈所示的远道区域，受噪声干扰，地震记录的有效信号难以分辨，初至同向轴连续性较差，难以辨识。利用常规的三维超虚折射干涉法和本文中基于方位角约束的三维超虚折射干涉法增强后的地震数据的信噪比均得到有效改善，相比于加噪的数据，对噪声得到了压制，初至波形的连续程度明显改善，初至波的同相轴可以被有效的识别。从增强的地震记录和原始理论数据的波形连续性和信噪比对比来看，基于方位角约束的三维超虚折射干涉法增强的效果要优于常规的三维超虚折射干涉法，这是因为加入方位角的约束避免了大量非近似传播路径的折射波参与叠加引入干扰。

为了对比不同初至波增强方法增强得到的数据对初至拾取精度的影响和拾取的效果，采用STA/LTA与多道互相关结合的方法[17]拾取增强后数据的初至，并将拾取的初至与理论数据拾取的初至结果进行做差对比，如图6(a)所示，拾取的误差分布如图6(b)、(c)所示。通过拾取的误差比较可以看到，常规方法增强初至拾取的误差较大，基于角度约束增强后拾取的精度要优于常规方法增强后拾取的精度，且96%的初至拾取误差小于±12.5 ms，即正演模拟所采用震源子波主周期的四分之一(主频20 Hz地震子波的主周期T为50 ms)。尤其值得注意的是，图6(b)显示的初至误差整体小于零，这表明不加方位角约束时引入了折射波的非共同路径，导致增强后初至波产生了整体的时移。该问题通过引入方位角约束得到了较好的改善，如图6(c)所示。

通过初至拾取的对比，说明本文中基于方位角约束的三维超虚折射干涉法在对在层状模型下的低信噪比三维地震数据进行初至波增强后，能够有效重构出初至波，且相比于常规的三维超虚折射干涉法能够提高初至波增强的准确度。

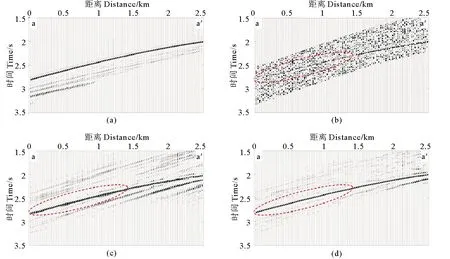
((a)原始理论数据;(b)加噪初至地震记录;(c)常规三维超虚折射干涉法增强后的地震记录; (d)基于方位角约束的三维超虚折射干涉法增强后的地震记录。红色虚线圈指出了信噪比变化明显的区域。(a) Raw data after time windowing; (b) Adding noise first arrival data after time windowing; (c) Data enhanced by the conventional 3D supervirtual refraction interferometry enhance; (d) Data enhanced by 3D supervirtual refraction interferometry based on the constraint of azimuth. The red dotted circles indicate areas where the SNR changed significantly.)

((a)初至误差(蓝色“+”为常规方法增强后拾取误差；红色“·”为基于方位角约束增强后拾取误差)；(b)常规方法增强后初至误差分布；(c)基于方位角约束增强后初至误差分布。(a) Picking errors (Blue “+” represents picking errors of data enhanced by the conventional method; Red “·” represents picking errors of data enhanced by the method based on the constraint of azimuth); (b) Distribution of picking errors of data enhanced by the conventional method; (c) Distribution of picking errors of data enhanced by the method based on the constraint of azimuth.)

2.2 模型2：多层模型

由于在实际情况下地下介质速度为连续变化，这将导致仅基于方位角约束的三维超虚折射干涉法中方位角的约束不足，为测试本文基于方位角和偏移距联合约束的三维超虚折射干涉法在地下介质速度为层状连续变化的地震数据增强效果，构建了如7(a)所示多层速度模型，模型的大小为8 km×12 km×3 km。三维正演模拟中所采用的观测系统如图所示，其中检波点间距为20 m，测线间距为200 m，在Y、X方向上，炮点间距分别为80和120 m，共有400个炮点。每一炮的接收范围为大小为4 km×6 km，共 21条测线，每条测线为301个检波点，共6 321个检波点。正演采用伪谱法正演[16]，震源子波采用主频为20 Hz的雷克子波。同样对理论数据添加了75%随机噪声，并对加噪数据进行了初至截取。图7(c)为抽取的图7(b)中所示a-a’、b-b’、c-c’ 三条测线进行初至截取后的地震记录，截取初至的窗口的位置如图7(c)中的黑色虚线位置所示，可以看到加噪数据的信噪比较低，远偏移距处初至信号较差。

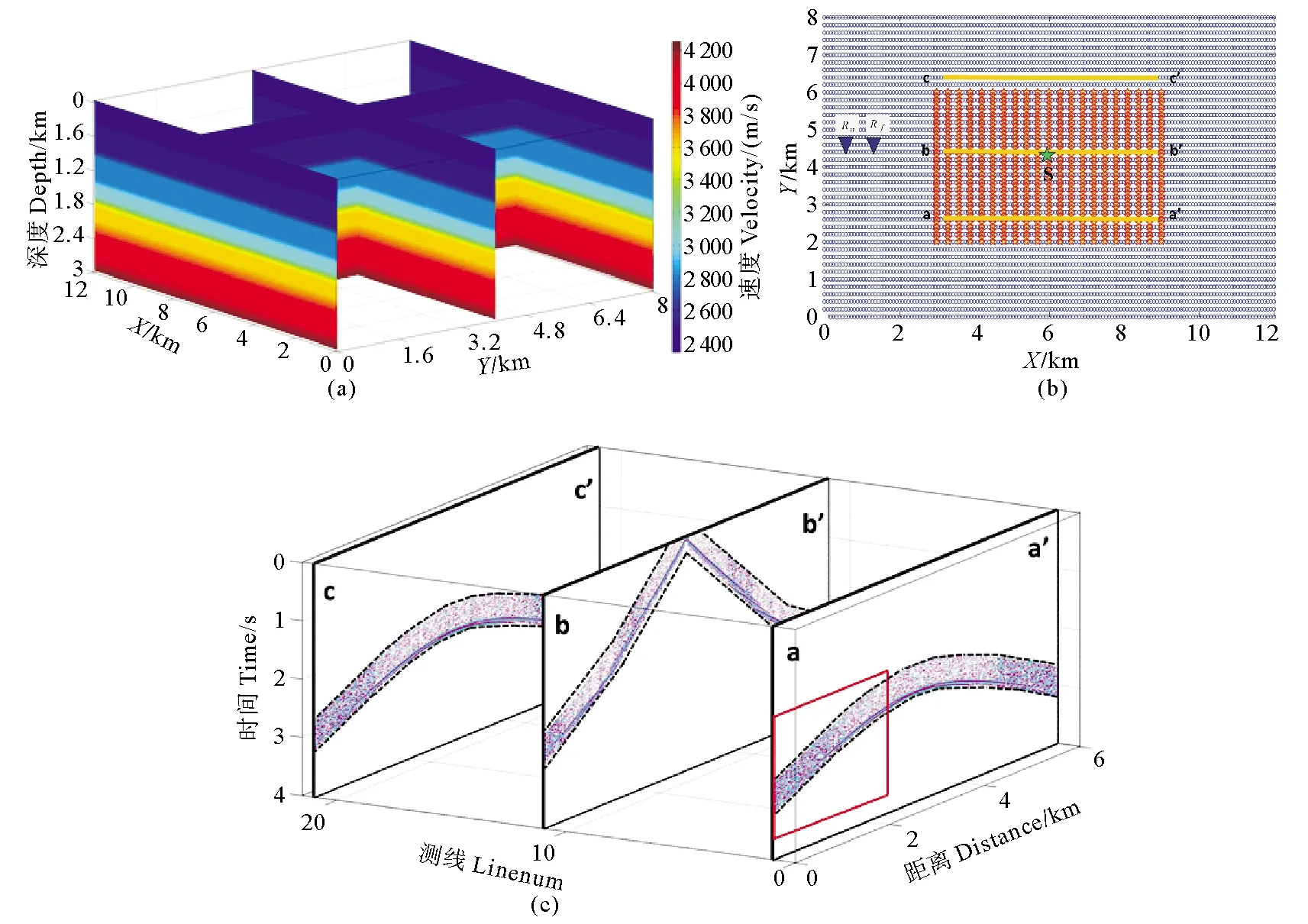
((a)多层速度模型；(b)观测系统(图中红色星为炮点，蓝色点为检波点；深蓝色三角代表图8中生成虚拟道的两个检波点位置；增强测试所选择的炮点和测线分别为绿色星和黄色测线)；(c)理论数据加噪后截取初至的地震记录(黑色虚线为截取初至的窗口,红色方框为局部放大显示的区域。)。(a) Multilayer velocity model; (b) Geometry (Red star represents source, Blue point represents receiver; Dark Blue triangle represents the positions of the two receivers that generate the virtual trace inFig 8; The source and survey lines selected for the enhancement test are green star and yellow lines respectively);(c) Adding noise first arrival data after time windows (The black dashed line shows the boundary of the time window; The red box is the area that is zoomed.).)

为研究在速度渐变介质下偏移距对初至波增强的影响，选择如图7(b)中Rn、Rf两检波点对。首先，将两检波点对初至折射互相关生成的虚拟道集按照方位角∠SRfRn排列，方位角限制为10°范围内，如图8(a)所示。可以看到虚拟道集在10°范围内，其峰值时间排列不一致，较为杂乱，直接进行虚拟道集的叠加会影响叠加虚拟道的准确度。将虚拟道集按照炮点到两检波点对Rn、Rf的中点之间偏移距(虚拟道偏移距)排列，如图8(b)所示。可以看到，随着虚拟道偏移距的增大，有两个明显的峰值时刻，这是因为存在不同的折射层，随着偏移距的增大，虚拟道之间存在差异。在虚拟道的峰值时刻一致的偏移距段范围内分别进行虚拟道的叠加，如图8(b)中的红色虚线框所示，可以实现同相叠加，这样能够有效压制噪声，提高虚拟道的信噪比、准确性。

在针对速度渐变介质下的初至波增强时，需要先选取一个较小的方位角范围筛选虚拟道，然后将筛选得到的虚拟道随偏移距排列，将虚拟道的峰值时刻排列一致的偏移距范围作为选取偏移距的依据。再根据偏移距范围内的虚拟道的峰值时刻排列来调整方位角，最终选择合适的方位角和偏移距，然后进行虚拟道的叠加。

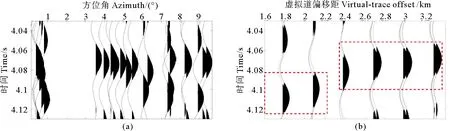
(虚拟道所对应检波点对如图7中Rn、Rf所示。(a)按方位角排列的虚拟道集(方位角10°范围的虚拟道);(b)相同虚拟道集按偏移距排列显示。(a) Virtual traces arranged by azimuth (The virtual traces in the azimuth range of 10°); (b) Virtual traces arranged by virtual-trace offset.)

接下来进行初至波增强测试，图9(b)为图7(c)中红色方框区域局部放大，原始的理论数据如图9(a)所示。利用基于方位角约束的三维超虚折射干涉法初至波增强后的结果如图9(c)，基于方位角和偏移距联合约束的三维超虚折射干涉法初至波增强后的结果如图9(d)。可以看到加噪理论数据的信噪比较低，尤其是红色虚线圈所示的远道区域，受噪声干扰，地震记录的有效信号难以分辨，初至同向轴连续性较差，难以辨识。进行初至增强后的地震数据的信噪比都得到有效改善，相比于加噪的数据，噪声得到了压制，初至波形的连续程度明显改善，初至波的同相轴可以被有效的识别。从图9(c)、(d)对比可以发现，图9(d)中1～2 km范围有些位置的信噪比提升效果差于图9(c)。这是因为加入了偏移距的约束，筛选进行叠加的地震道变少，叠加压制噪声的效果弱于图9(c)，但是图9(d)增强结果的拾取精度要优于图9(c)，如图10初至拾取结果所示。

((a)原始理论数据;(b)加噪初至地震记录;(c)基于方位角约束的三维超虚折射干涉法增强后的地震记录; (d)基于方位角和偏移距联合约束的三维超虚折射干涉法增强后的地震记录(红色虚线圈指出了信噪比差异明显的区域)。(a) Raw data after time windowing; (b) Adding noise first arrival data after time windowing; (c) Data enhanced by 3D supervirtual refraction interferometry based on the constraint of azimuth enhancement; (d) Data enhanced by 3D supervirtual refraction interferometry based on the joint constraint of azimuth and offset. (The red dotted circles indicate areas where the SNR changed significantly.).)

使用STA/LTA与多道互相关结合的方法[18]拾取增强后数据的初至，并与理论数据拾取的初至结果进行误差比较，如图10(a)所示，拾取的误差分布如图10(b)、(c)所示。通过误差分布的比较，可以看到进行方位角约束初至波增强后，初至拾取误差有约88%小于±12.5 ms；基于方位角和偏移距联合约束增强后，初至拾取误差有约93%小于±12.5 ms，基本都能满足小于正演模拟所采用震源子波主周期四分之一的要求(主频20 Hz地震子波的主周期T为50 ms)。说明利用本文提出的基于方位角和偏移距联合约束的三维超虚折射干涉法在对地下为多层速度介质情况下低信噪比的三维地震数据进行初至波增强后，能够有效重构出准确的初至波。

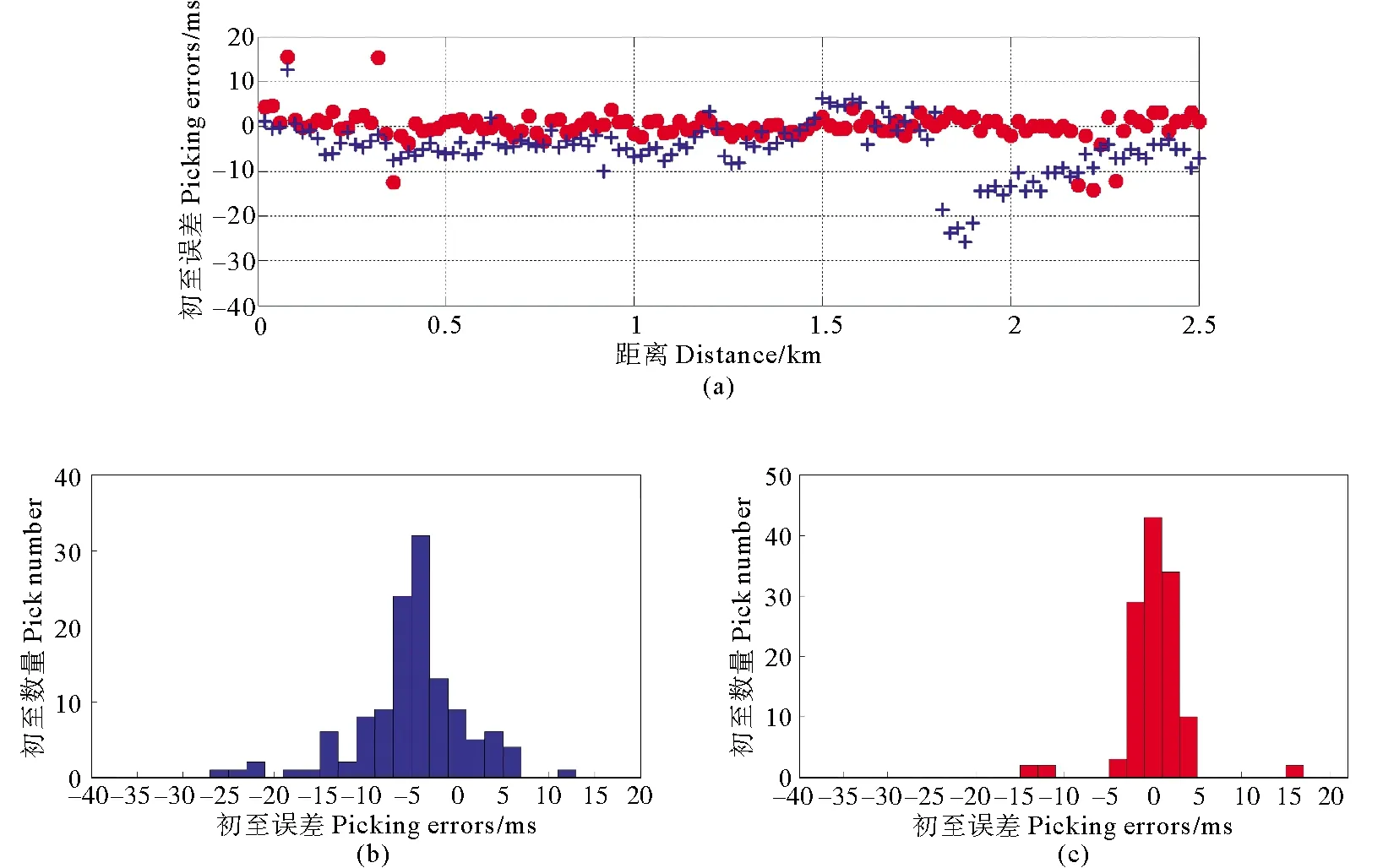
((a)初至误差(蓝色“+”为基于方位角约束增强后拾取误差；红色“·”为基于方位角和偏移距联合约束增强后拾取误差)；(c)基于方位角约束增强后初至误差分布；(d)基于方位角和偏移距联合约束增强后初至误差分布。(a) Picking errors (Blue “+” represents picking errors of data enhanced by the method based on the constraint of azimuth; Red “·” represents picking errors of data enhanced by the method based on the joint constraint of azimuth and offset.) (b) Distribution of picking errors of data enhanced by the method based on the constraint of azimuth; (c) Distribution of picking errors of data enhanced by the method based on the joint constraint of azimuth and offset.)

2.3 子波主频对于初至增强的影响

在初至增强的过程中，受子波主频影响的步骤是互相关生成虚拟道时，而卷积增强时利用高信噪比的参考道和δ函数(虚拟道加窗口后的结果)做卷积，该过程子波主频对结果影响不大。为了探讨不同子波主频的地震道互相关时结果的稳定性，分别利用10、20、40和80 Hz子波主频的地震道添加75%随机噪声地震道进行互相关(75%指的是添加的随机噪声的最大振幅值与地震道绝对值的最大振幅比)，并与未加噪的互相关结果对比。进行互相关的地震道采用雷克子波模拟，采样率为0.002 s，地震道的长度为0.6 s，设定的互相关地震道之间相对时差为0.12 s。

互相关后结果如图11所示，图11(a)与(b)显示在主频10和20 Hz时，加噪进行互相关的结果也能够较好刻画出互相关的峰值时刻；而随着频率变高，在主频40和80 Hz时，加噪后互相关的结果峰值时刻难以刻画，如图11(c)与(d)所示。从图11结果显示，在低频时，地震道互相关的结果受随机噪声的影响较小，稳定性较好；随着频率的升高，稳定性变差。因此，在初至增强的时候，震源子波的主频升高会对虚拟道的准确性产生不利影响，这也将会使得增强的初至波不准确。

然而，在初至增强的实际过程中，对互相关后的虚拟道进行了叠加，为验证叠加对噪声压制效果，进行了叠加测试。图12所示为叠加的结果，其中叠加的次数为20。对比图11、12，结果表明，叠加对互相关后虚拟道的噪声能够有效压制。尤其在子波主频变高时，即在40和80 Hz时，叠加后的结果也能够较好刻画出互相关的峰值时刻。在初至增强的过程中，叠加能够对虚拟道的噪声有较好的压制作用，从而提高虚拟道的准确性，这将能保证初至增强的准确度。

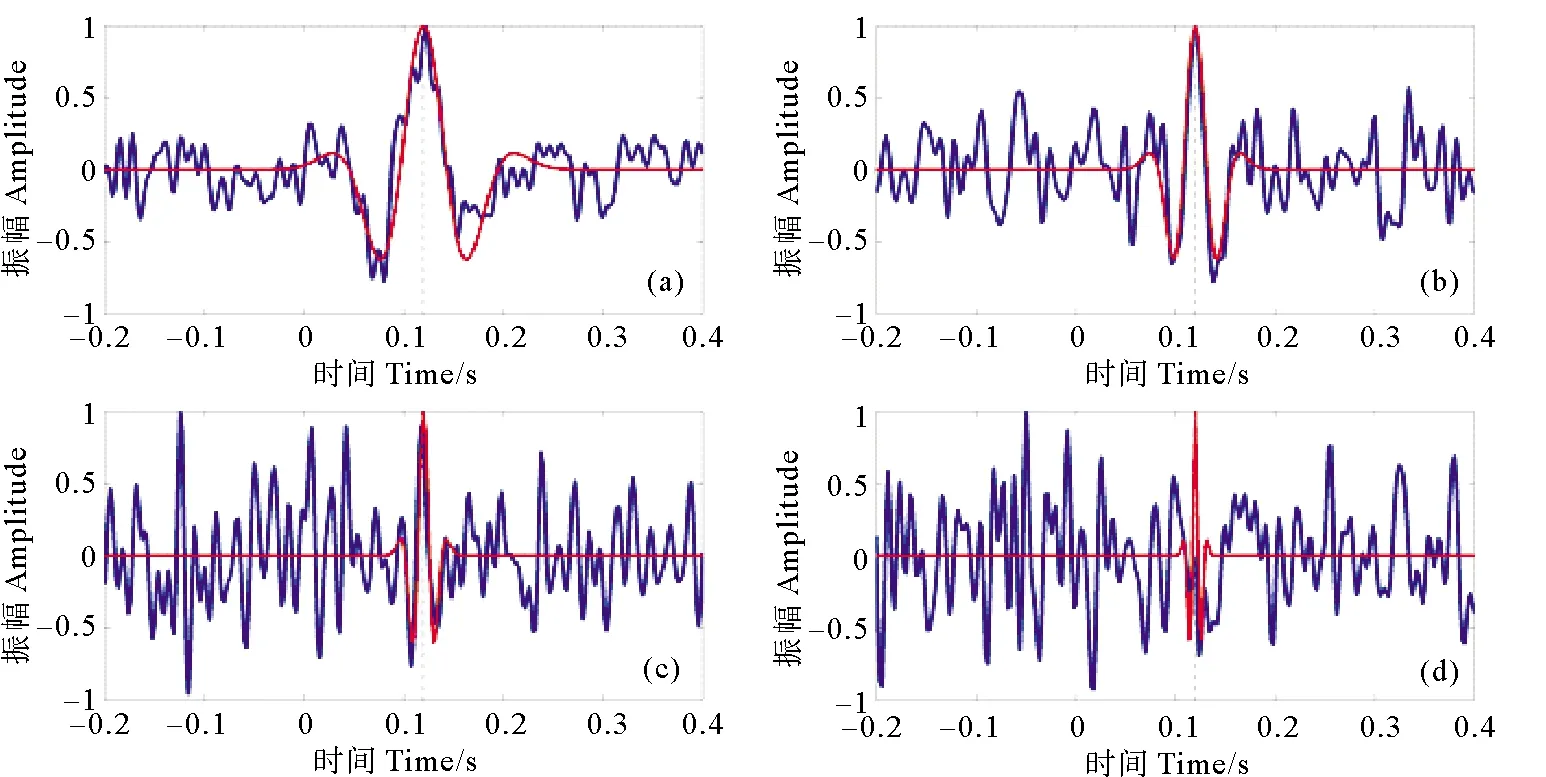
((a)主频10 Hz；(b)主频20 Hz;(c)主频40 Hz；(d)主频80 Hz。(红色道为原始地震道互相关结果，蓝色道为地震道加噪75%互相关结果。)。(a) Central frequency 10 Hz; (b) Central frequency 20 Hz; (c) Central frequency 40 Hz; (d) Central frequency 80 Hz.(The red and blue lines are the cross-correlation results for the noise-free data and the data adding 75% noise.).)

((a)主频10 Hz；(b)主频20 Hz;(c)主频40 Hz；(d)主频80 Hz。(红色道为原始地震道互相关结果；蓝色道为地震道加噪75%互相关叠加结果，叠加次数为20次。)。(a) Central frequency 10 Hz; (b) Central frequency 20 Hz; (c) Central frequency 40 Hz; (d) Central frequency 80 Hz.(The red and blue lines are the cross-correlation results for the noise-free data and the data adding 75% noise，stacking number is 20.).)

3 实际数据测试

为验证本文中方法对实际资料的初至波增强效果，将本文基于方位角和偏移距联合约束的三维超虚折射干涉法应用于西部某区域采集的三维地震资料数据。三维地震资料的工区采集观测系统如图13(a)所示，观测系统中检波点间距为20 m，测线间距为200 m，炮点间距在X、Y方向分别为300、100 m，炮点个数为4 756炮，工区大小约176 km2。图13(b)为抽取的图13(a)中绿色星所指炮点位置处的a-a’、b-b’、c-c’三条测线进行初至截取后的地震记录，可以看到数据的远偏移距处的初至的信噪比较低，这将会制约初至的拾取。

对数据进行了初至波增强测试，图14(a)为图13(b)中a-a’测线的红色方框局部区域放大图。利用本文的基于方位角和偏移距联合约束的三维超虚折射干涉法进行初至波增强后的地震记录如图14(b)所。在进行初至增强时，该区块三维实际地震资料增强所选择的方位角的角度为5°，偏移距段范围为1～2 km，2～6 km(2 km-最远偏移距范围)。可以看到，在原始的地震记录中远道位置处的初至受到噪声干扰，初至难以辨识，如图14(a)红色虚线圈所示位置。利用本文基于方位角和偏移距联合约束的三维超虚折射干涉法进行初至波增强后，对噪声干扰得到了有效的压制，地震数据的初至波相比于原始数据信噪比得到了明显提升，如图14(b)中红色虚线圈所指示位置，且初至波增强后的地震记录初至波同相轴连续可辨。

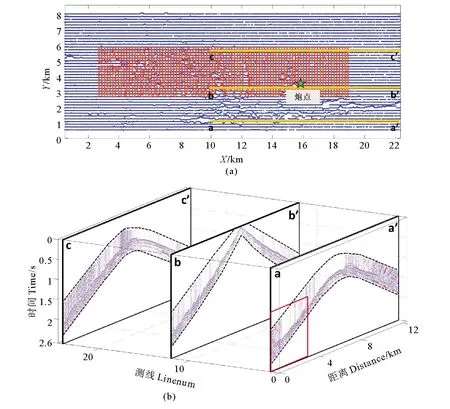
((a)观测系统(蓝色点为检波点位置；红色点为炮点位置；增强展示选择的炮点和测线分别为绿色星和黄色测线);(b)原始数据截取初至后的地震记录(黑色虚线为截取折射初至的窗口,红色方框为局部放大显示的区域)。(a) Geometry. (Red dot represents source, Blue dot represents receiver; The source and survey lines selected for the enhancement test are green star and yellow lines respectively); (b) Original seismic data after time windows. (The black dashed line shows the boundary of the time window; The red box is the area that is zoomed.).)

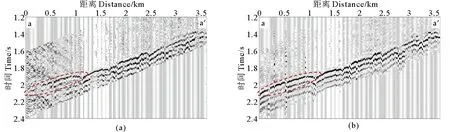
((a)原始数据截取初至后的地震记录；(b)基于方位角和偏移距联合约束的三维超虚折射干涉法增强后的地震记录(红色虚线圈指出了信噪比变化明显的区域)。(a) Original seismic data after time windows; (b) Data enhanced by 3D supervirtual refraction interferometry based on the joint constraint of azimuth and offset. (The red dotted circles indicate areas where the SNR changed significantly.).)

为了对比初至波增强前后初至拾取的差异，抽取了测线a-a’进行初至波增强前后初至拾取对比。我们用初至自动拾取方法[18-19]，对初至波增强前后的地震数据进行了初至拾取，如图15所示。拾取结果显示，原始数据中的远道信噪比较低，受噪声干扰严重，导致远道数据的初至无法准确拾取，且有部分位置无法进行初至拾取，如图15(a)中红色虚线圈范围内的拾取情况所示。利用基于方位角和偏移距联合约束的三维超虚折射干涉法进行初至波增强后，地震记录的远道信噪比有较好的改善，初至波的同相轴连续且清晰可辨，原始数据中无法识别的初至得到了增强，可以进行有效拾取，拾取的效果得到了较好的改善，如图15(b)所示。因此，应用本文基于方位角和偏移距联合约束的三维超虚折射干涉法对初至波进行增强后，能够扩大低信噪比的地震数据初至拾取的范围。

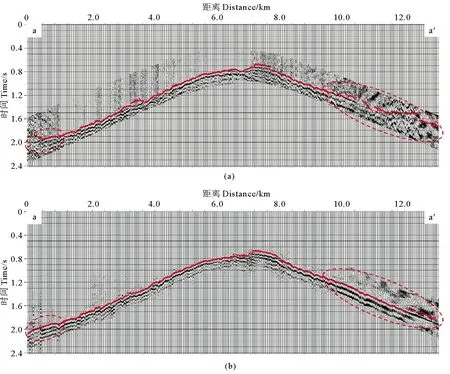
((a)原始地震记录初至拾取；(b)基于方位角和偏移距联合约束的三维超虚折射干涉法增强后拾取初(红色点为初至拾取结果的投影，红色虚线圈指出了信噪比变化明显的区域)。(a)First arrival picking on original data; (b) First arrival picking on data enhanced by 3D supervirtual refraction interferometry based on joint constraint of azimuth and offset.(Red dots represent first arrivals’ time; The red dotted circles indicate areas where the SNR changed significantly.).)

综上所述，本文提出的基于方位角和偏移距联合约束的三维超虚折射干涉法应用于实际三维地震资料初至波增强时，能够对原始数据的强噪声有较好的压制作用，有效提高低信噪比地震数据的信噪比，进行初至增强后的初至波清晰可辨、同相轴连续，能够有效扩大低信噪比低的地震数据的初至拾取范围，提高初至拾取的数量，将有利于提高后续速度建模的准确度、稳定性。

4 结语

目前广泛应用的三维地震勘探中，地震数据远偏移距的初至波信噪比较低。针对二维超虚折射干涉法不适用于三维的观测系统，无法对采集的三维地震数据进行初至增强的问题，本文基于超虚折射干涉法的理论假设，提出了基于方位角和偏移距联合约束的三维超虚折射干涉法。通过方位角和偏移距约束筛选炮点和检波点，满足了三维超虚折射干涉法对折射波路径重合的要求，实现了对目标地震道的重构，显著提高了三维地震数据的初至波信噪比。理论和实际数据的应用均表明，增强后的数据可以使地震初至拾取的准确度明显提高，对于高效速度建模具有重要意义。地震道范围的约束导致了最终虚拟道叠加次数的降低，会在一定程度上降低超虚折射干涉法的抗噪能力，后续可以借鉴相邻虚拟道叠加等方法进一步提高虚拟道叠加次数来对本方法进行改进。