基于GBDT算法的空气冲旋钻井机械速度预测方法
2022-06-27夏冰
夏 冰
(郑州升达经贸管理学院 信息工程学院,郑州 451191)
0 引言
随着社会对能源需求量的大幅增加,钻井勘探逐渐从浅层挖掘逐渐向深层和更深层挖掘,以此来满足日益增长的能源需求。我国的石油勘探开采领域也正在向深层、超深层以及非常规的方向发展。
石油的钻井开采是一项投资巨大且伴随着高风险的作业,钻井过程中产生的费用也是相当高的。随着钻井深度的逐渐加深,周围环境的压实度、磨蚀性以及开采难度越来越高,钻井机械难以根据岩层厚度或密度实时预测和调整转速,使得钻井速度变慢、开采周期变长,甚至出现大斜率井体,难以安全获得需要的矿产资源。因此,为在坚硬且严重倾斜的地层中降低井斜角,设计一种有效的钻井机械速度预测方法意义重大。
文献[1]中设计了基于BAS-BP的钻井机械钻速预测方法。该方法首先利用小波滤波算法对钻井现场数据进行过滤处理,消除其中的噪声数据。然后利用互信息关联算法为钻速预测模型选取最优输入参数。最后利用天牛须搜索算法优化处理BP神经网络中的阈值,以此来求解预测模型。文献[2]中针对巨厚砾石层设计了一种钻井速度分析技术。在明确地层形态结构的基础上,将其划分为未成岩段、准成岩段以及成岩段三种砾石层形态。然后针对这三种地层形态分配钻井系统和钻井工具,并连接蜗轮和孕镶钻头、双摆工具,以便精准预测当前岩体对应使用的钻头转速。
然而在实际应用中发现,上述两种传统方法难以实时调整空气冲旋钻井机械参数,导致其难以灵活应对各类密度、斜率岩层,泛化能力较差。针对这一问题,本研究提出了基于梯度提升树(Gradient Boosting Decision Tree,GBDT)的空气冲旋钻井机械速度预测方法。该方法在建模分析空气冲旋钻井机械的基础上,针对不同类型的冲旋钻头齿头,在经过一系列的平移、旋转处理后,使齿头坐标点全部落在冲旋钻头上。然后利用GBDT算法具有的响应速度快、容错能力强以及树深浅的特点,建立钻井机械速度预测模型。通过与其他方法进行对比后发现,该方法具有理想的拟合度和预测精度。同时,在调整模型参数后,该方法也取得了非常优秀的泛化能力,在优化钻井速度、提高石油产量方面,提供了一种科学合理的参考意见。
1 构建空气冲旋钻井机械模型
空气冲旋钻井机械的钻速与冲旋钻头密切相关,钻头参数影响着机械的钻速,例如齿圈的齿头数量、齿形等。因此,本研究在对冲旋钻头进行离散化处理后,对其展开建模分析。
在本研究中,主要对钻头球形齿和圆锥齿展开建模分析。其中,球形齿模型的定义公式为:
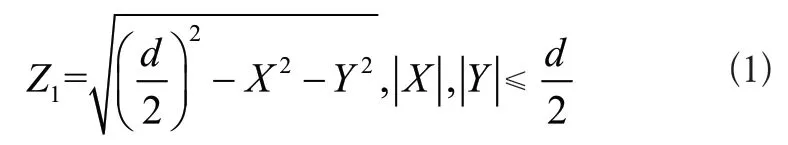
式(1)中,d表示球形齿的直径大小;X、Y、Z共同构成球形齿模型的三维坐标系。
圆锥齿模型的定义公式为:
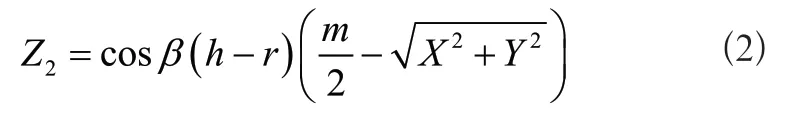
式(2)中,m表示圆锥底面直径大小,h表示圆锥的高,r表示圆锥顶圆的半径大小,β表示锥顶角。
在静态坐标系下分析冲旋钻头齿头的位置信息,如图1(a)所示。从外向内对冲旋钻头齿圈进行编号,并用j=1,2,…表示,按照顺时针方向,从冲旋钻头初始齿圈开始进行转动,得到的编号用k=1,2,…,nj表示。X轴经过钻头第一圈一颗齿头的中心点,Y轴根据右手坐标系确定得到,因Z轴与静坐标系的Z轴重叠在一起,所以图中没有显示。通过上述即可确定每个冲旋钻头中所有齿头的中心坐标(ρ,θ,z)为:

图1 冲旋钻头模型
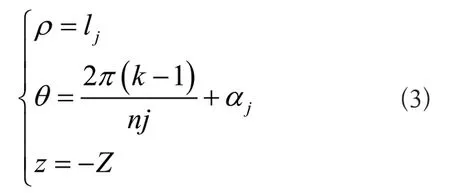
式(3)中,lj表示第j圈齿圈的直径大小,αj表示第j圈齿圈中第一颗齿头与X轴之间形成的夹角,nj表示第j圈齿圈中的齿头总数。
图1(b)中,通过直角坐标系O-XYZ对钻头钻进石油井底时钻头位置发生变化描述。钻头的轴心线与Z重叠在一起,将M看作是冲旋钻头上的随机点,圆柱坐标为(ρm,θm,Zm),θm表示的是极角,转动方向为顺时针。那么直角坐标系为(Xm,Ym,Zm):

获取M点的标高,将其在直角坐标系OXYZ上的初始高度看作是冲旋钻头的标高,用Z0来表示。基于此就可以通过观察M点在Z轴上的变化来确定冲旋钻头的进尺。
将第j圈齿圈上第k颗齿头轮廓面的离散点看作是Tjkm,经过平移和旋转处理后,将坐标系中牙齿的点全部变换到冲旋钻头上,离散点变换为T*jkm,过程如下:

式(5)中,Rjk表示第j圈齿圈上第k颗齿头在冲旋钻头上的位置变换矩阵[3],用齐次坐标进行描述,共包含平移变换矩阵、绕Y轴旋转变换矩阵、绕Z轴旋转变换矩阵以及绕任意轴旋转变换矩阵4个矩阵在内。
通过上述过程,冲旋钻头齿头上的随机点经过X、Y、Z轴平移后、绕Y轴旋转φ角、再绕Z轴旋转ψ角、最后绕余弦方向上的任意轴旋转θ角后可以得到新的位置坐标点,此时坐标系中的齿头点就变换到冲旋钻头上,进而得到由若干个离散点描述的空气冲旋钻井机械模型。
2 基于GBDT算法预测空气冲旋钻井机械速度
2.1 GBDT算法分析
GBDT算法通过基函数线性组合的方式,在计算过程中不断的减小残差,达到数据分类和回归的目的[4]。GBDT算法的计算过程如图2所示。

图2 GBDT算法计算过程
GBDT算法的计算过程离不开弱分类器,本研究中选择CART TREE弱分类器,这种分类器具有低方差、高偏差,同时树的深度很浅的优势,非常适用于GBDT算法的计算过程。通过基函数线性组合得到的算法分类器为:

式(6)中,xf表示弱分类器,ωx表示弱分类器初始化权重,W表示弱分类器组合系数。通过前一轮分类器产生的残差对当前分类器进行计算,整个过程凭借梯度下降法进行计算[5]。换句话说,利用分类器损失函数中的负梯度值,作为回归问题提升树算法中的残差近似值,获取得到一个新的回归树。
2.2 空气冲旋钻井机械速度预测模型
根据以往研究内容中可以发现,空气冲旋钻井机械的钻速与机械工作参数之间存在着十分复杂的关系。本研究利用GBDT算法来构建速度预测模型,凭借算法的适应能力强、学习能力强、容错性强以及响应速度快等优点,通过对采集到的钻井现场数据进行反复训练,明确机械工作参数与钻速之间关系。
表1为某种型号的空气冲旋钻井机械在工作状态下的各项参数。
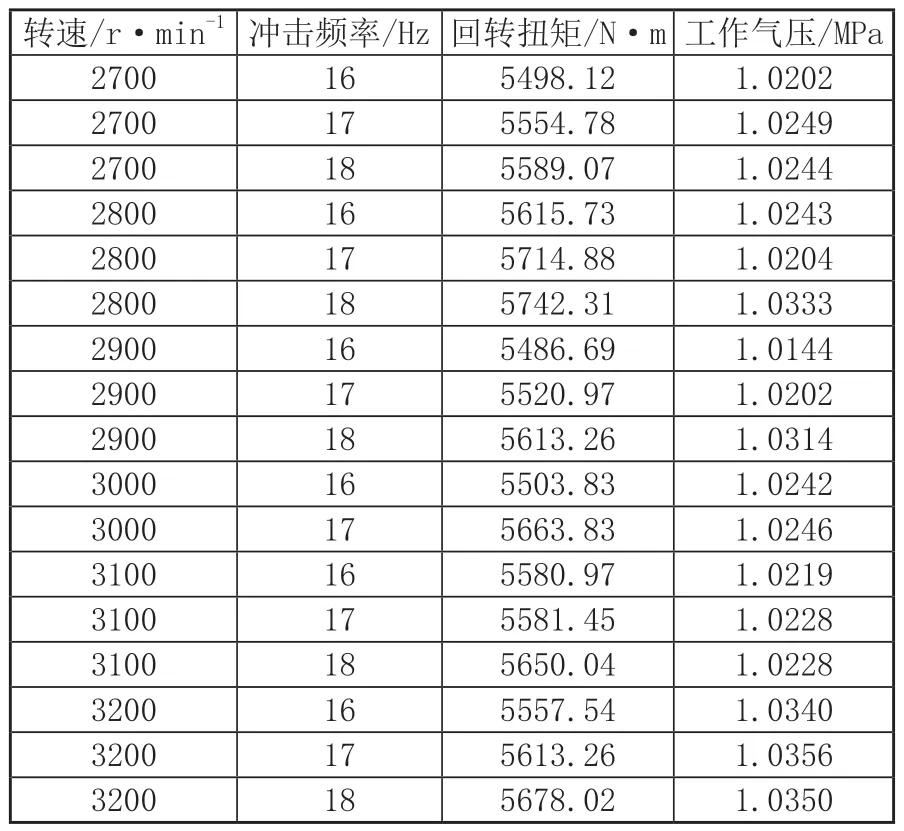
表1 空气冲旋钻井机械参数
空气冲旋钻井机械的钻进过程受多方面因素控制,伴随着的工作参数也有很多。在工作参数基础上分析得到的钻井机械速度预测模型为:
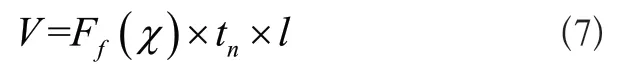
式(7)中,V表示钻井速度,tn表示钻进时间,l表示钻进进尺。
3 实验与分析
为了验证基于GBDT算法的空气冲旋钻井机械速度预测方法在实际应用中的有效性,设计如下基础测试实验与对比测试实验。实验环境如图3所示。

图3 实验现场环境
实验中使用的空气冲旋钻井相关参数如下:
钻头型号为三牙轮钻头,钻压为49.2kN,钻孔深度为220米,回转转速为2650r/min,回转扭矩为5500N·m,提升力为10~15t,冲击频率为28Hz,冲击功为1260J。
3.1 基础测试
步骤一:在本研究构建的钻井速度预测模型中导入数据。实验中用到的数据均来自于河南中原油田的真实数据。
步骤二:利用十倍交叉检查法,结合GBDT算法独有的特性,在无需对数据进行预处理的情况下直接划分其为测试集和训练集。每次训练均进行10次。
步骤三:建立GBRT(Gradient Boosting Regression Tree)模型,利用Python Sklearn包来实现模型的运行。
步骤四:为了更直观地描述本文方法的预测性能,通过图4的形式绘制了本文方法所得预测值与实际值之间的关系图。

图4 本文方法预测值与实际值关系图
通过观察图4可以看出,利用本文方法预测的钻井机械速度与实际值非常的接近,几乎所有的预测点都落在了实际值的线上,这说明两个值基本一致,证明了本文方法具有非常高的预测精度。对于没有落在实际值线上的点,二者之间相差也都较小,同样也可说明本文方法具有较高的拟合效果。
3.2 对比测试
为了进一步突出本文方法的预测性能,将其与基于BAS-BP的钻井机械钻速预测方法(文献[1]方法)、钻井提速技术分析方法(文献[2]方法)展开对比。
首先对比不同方法预测结果与真实结果之间的拟合度,结果如图5所示。
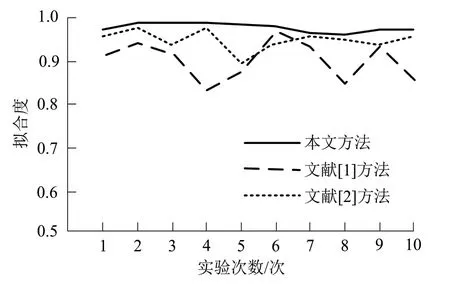
图5 不同方法的拟合度对比结果
从图5中可以看出,文献[1]方法和文献[2]方法得到的预测结果与实际值之间的拟合度虽处于80%以上,但是相比而言,文献[1]方法的拟合度更低,而二者的拟合度均小于本文方法。根据曲线变化情况可以发现,本文得到得到的预测结果与实际值之间的拟合度在前期一直保持平稳的状态,第7,8次实验中出现了少许的下降,但整体的拟合度数值始终保持在95%以上,由此可以说明,本文方法的拟合度要优于其他两种方法,更能准确预测空气冲旋钻井机械的速度。
接下来从泛化能力方面对三种方法展开测试。在钻井速度预测模型使用过程中,调参是必不可少的一个过程。为此,实验在网格搜索法的基础上,从弱分类器数量、决策树的最大深度、参数步长以及内部节点等几个方面对预测方法的运行参数作出调整,并选择两个石油井进行测试,来比较参数调整前后方法的泛化能力。参数调整前后对比如表2所示。

表2 参数调整前后对比
然后再以拟合度为指标,对参数调整后方法的预测能力进行测试,结果如图6所示。
通过对比图6和图5可以发现,在调整方法的运行参数后,虽然本文得到得到的预测结果与实际值之间的拟合度有所下降,但整体仍保持平稳状态,且拟合度数值仍在95%以上,而两种传统方法的拟合度存在明显的下降情况,这说明本文方法具有较强的泛化能力,大大降低了过拟合的几率,使得预测质量可以维持在较高的水平。
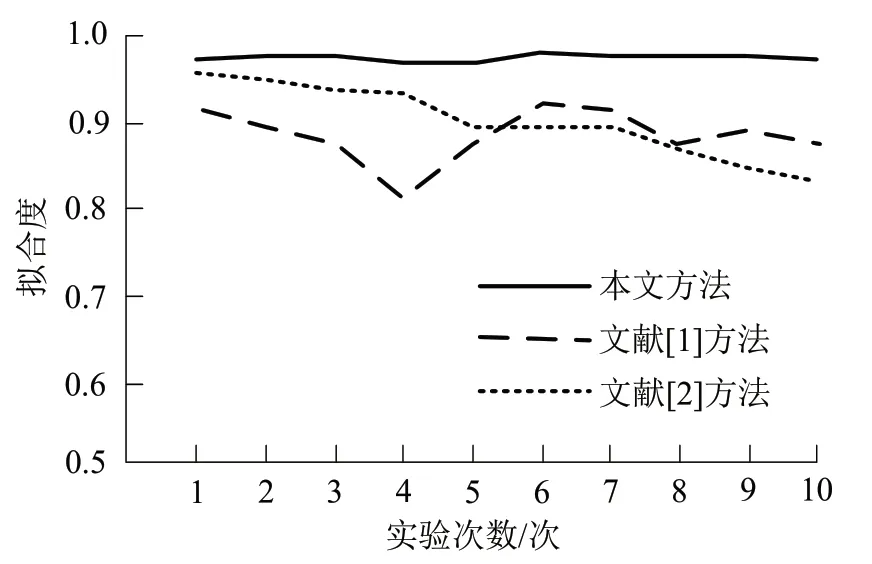
图6 参数调整后不同方法的拟合度对比
4 结语
本研究利用GBDT算法对空气冲旋钻井机械速度进行预测,该方法可以快速、准确地分析得到各种影响钻井速度的因素。较其他方法来说,该方法取得的预测值与实际值之间具有非常高的拟合程度。不仅如此,在现场施工中,根据实际分析出的速度影响因素,可以帮助技术人员制定出一套更加科学合理的钻井方案,从而增加钻井速度、提高石油产量。GBDT算法可以从大量的数据中快速找到对钻井速度有意义的参数,并根据经验对其进行调整,以此提高算法的泛化能力。
由于实验中使用到的数据数量有限,存在一定的局限性,而且对于钻井速度的影响变化规律并未进行深究。因此,在后续的研究,将尝试使用高敏感振动传感器采集更多的数据,以便进行更深入的研究,进一步提升机械使用寿命和矿井安全性,提出更加科学合理的钻井方案。
