基于Abaqus的SiC阻氚涂层表面裂纹性能的研究

刘泽 唐琳 孙付春 张亚飞 余松科 母雪玲

基于Abaqus的SiC阻氚涂层表面裂纹性能的研究

刘泽1唐琳1孙付春2张亚飞1余松科1母雪玲1

1（成都大学电子信息与电气工程学院 成都 610106）2（成都大学机械工程学院 成都 610106）

在聚变反应堆中阻氚涂层服役期间，涂层表面的裂纹性能以及基底粗糙度是制约涂层服役周期的关键因素。基于Abaqus有限元模拟软件，构建了SiC/316L不锈钢阻氚涂层系统模型。通过对基底表面粗糙度的引入，重点分析了基底粗糙度和涂层表面裂纹之间的关系。结果表明：基底粗糙度对涂层表面裂纹的应变能释放率有显著的影响。当裂纹位于波峰时，应变能释放率最大；当裂纹位于波谷正上方时，应变能释放率最小。相比于光滑交界面，沿着粗糙界面的应力受到了一定程度的抑制效果，呈现降低的趋势。

SiC阻氚涂层，表面多重裂纹，应变能释放率，应力

氚作为核聚变反应中堆芯燃料之一，具有一定的放射性，并且在金属中有很强的渗透能力。如何阻止氚通过结构材料向外渗透是聚变装置中必须解决的重要问题。研究表明，氚在金属中以间隙原子的形式扩散，渗透能力较强，但在陶瓷材料中的渗透却是以类似分子的形式扩散，渗透率比在金属中低几个数量级［1］。因此，为了有效地阻止氚的渗透，同时不牺牲结构材料的整体性能，最实际的方法是在涉氚结构材料表面沉积一定厚度的氚扩散系数低的陶瓷涂层。但是，由于涂层和基底机械性能的差异，加上受到温度场的影响，涂层系统中不可避免地产生拉应力，当拉应力达到一定量级时会造成涂层表面产生裂纹。随着应力的增加，裂纹将不断扩展，进而造成涂层脱落等严重后果。

表面裂纹是涂层/基底系统中较为常见的失效方式。目前，国内外学者对涂层中裂纹的形成和扩展作了一定的研究。对于只考虑弹性性质的涂层/基底系统，当涂层中应力达到GPa数量级时，将足以诱导涂层中裂纹的产生［2］。Kawasak等［3］对热障涂层和金属基底所组成的系统进行了裂纹失效研究。结果表明：当系统温度上升时，涂层上表面会形成垂直裂纹。当温度下降时，涂层中会形成横向裂纹。Erdogan等［4］通过数理方程计算了恒定热载荷作用下，涂层中热应力强度因子、温度场和热应力场的理论解，并且发现周期裂纹对涂层表面应力松弛具有一定影响。Choules等［5］研究了涂层厚度与多重周期裂纹之间的关系。结果表明：增加涂层厚度可以有效地减少裂纹数量；并且发现裂纹之间的距离随着涂层厚度的增加而增加。以上的研究都是基于基底表面为完全光滑的假设得到的，具有一定的局限性。然而，在加工过程中基底表面的粗糙度无法避免。之前的研究结果表明，基底表面粗糙度不仅影响涂层系统中热应力的分布，而且还会改变涂层的机械性质［6-7］。因此，在研究涂层表面裂纹行为时，不能忽略基底粗糙度对涂层系统的影响。此外，Abaqus有限元模拟软件具有求解复杂工程问题的优秀能力，以及高效的非线性力学分析功能，适合本课题的需求。因此，本文选取SiC/316L不锈钢系统为研究对象，利用Abaqus数值模拟的软件，深入研究基底表面粗糙度与涂层表面多重裂纹性质之间的关系，为后期高稳定性阻氚涂层的开发奠定理论基础。

1 SiC阻氚涂层模型的建立

1.1　理论模型

在模拟过程中，首先对表面无裂纹的涂层系统进行计算。随后将外界载荷施加到涂层表面，0代表无裂纹状态下应力的大小。在表面的边界条件为［8］：

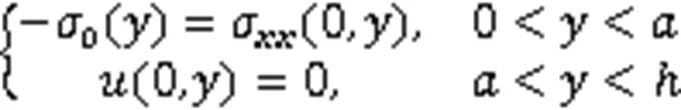
式中：σ代表模型中任意节点的应力分量；（，）代表某一节点（，）的位移；（0，）为模型中沿轴上某一节点的位移。

假设通过周期为2的正弦函数来代表基底表面粗糙度，每个周期中有1条裂纹。由于整体模型具有轴对称性及周期性的特点，坐标系中涂层/基底系统的长度区间为-～。当节点位于右边界=处，则与其对应的左节点处于=-位置。在平面中'和为位于对称轴左侧的节点。这两节点沿着轴的镜像的节点分别为和。节点之间的相互关系为［9］：

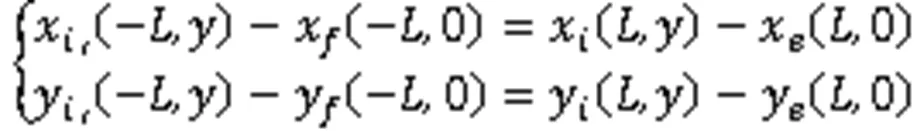
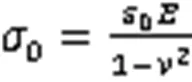
将涂层表面裂纹视为I型裂纹，对应的表征线弹性材料的裂纹尖端特征的应力强度因子为［11］：

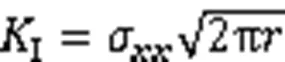
式中：代表计算求解的位置到裂纹尖端的距离。

裂纹的应变能释放率表示产生单位面积裂纹面所需要的能量，或延伸单位裂纹长度时所需要外载荷做的功，其计算方法为［12］：

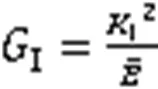
1.2　几何模型

如图1所示，为在Abaqus中建立的具有光滑和粗糙基底的SiC/316L不锈钢系统的2D模型。根据相关文献，粗糙的基底表面可以通过正弦函数来近似表达［6］。基底表面的正弦函数可以表示为：

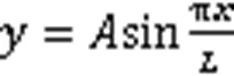
式中：代表振幅；代表半周期。

涂层表面的裂纹均平行于轴，且周期排列，长度为。在粗糙基底系统中，涂层的厚度定义为中心线到涂层顶端的距离，厚度为2 μm，基底厚度为0.5 mm。粗糙和光滑基底系统中，对应的涂层和基底厚度相等。为了模拟与现实更为接近，将基底底部的节点进行固定。并且，限制基底底部节点沿着轴和轴的旋转。在涂层表面施加沿着轴的均匀应变（=1%）。

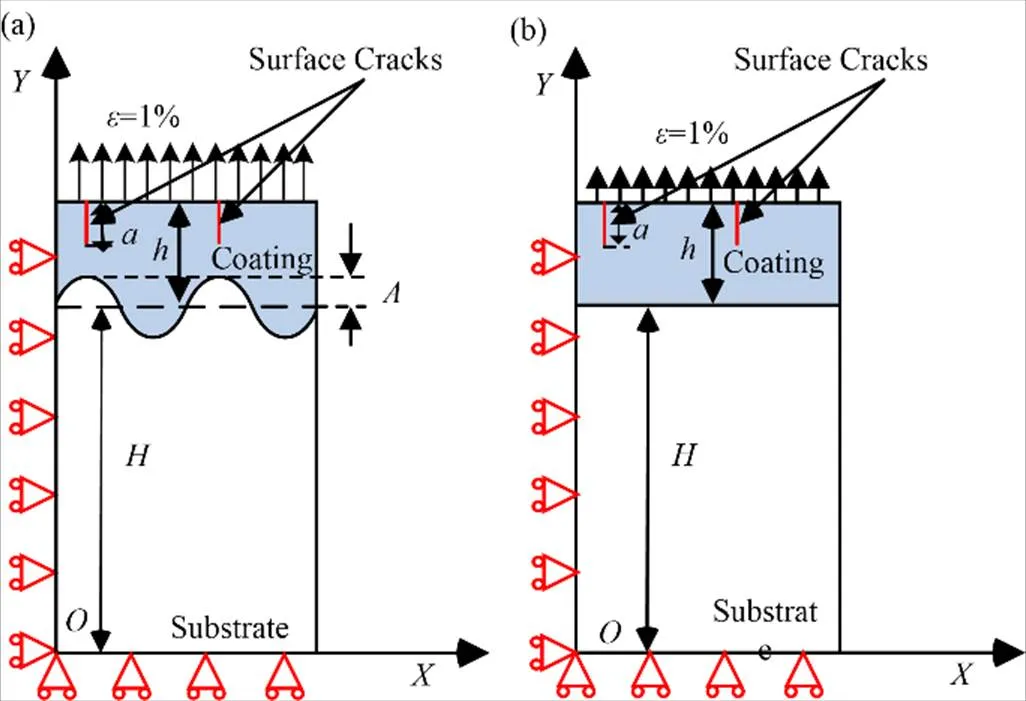
图1　具有多重表面裂纹的SiC阻氚涂层系统模型(a) 粗糙基底系统，(b) 光滑基底系统

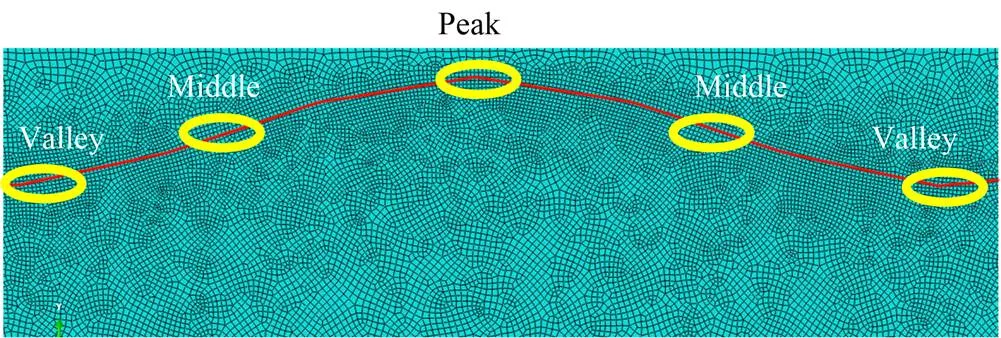
图2　对于具有表面周期裂纹的SiC涂层系统的网格划分(a) 粗糙基底系统，(b) 光滑基底系统

如图2所示，为具有粗糙和光滑基底系统中网格的划分情况。对涂层和基底区域应用四节点平面网格进行划分。如图3所示，为了后期便于分析，将SiC/316L不锈钢系统交界面区域进行定义。SiC和316L不锈钢的材料属性见表1。

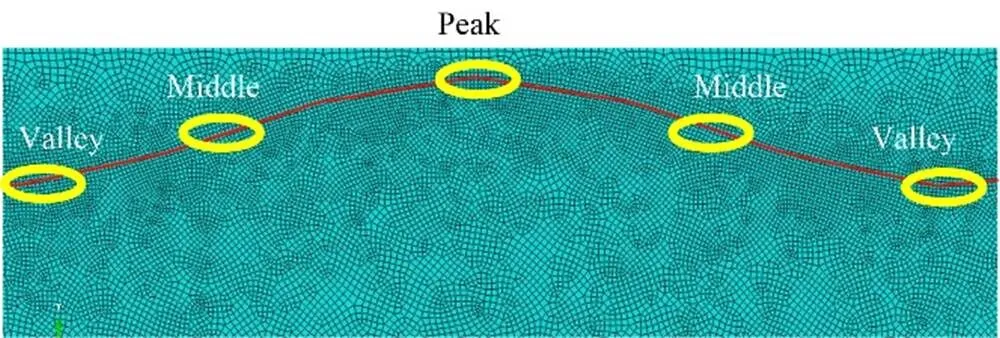
图3　对涂层与基底交界面不同位置的定义

表1 材料属性[13‒15]

2 结果与讨论

2.1　粗糙基底对应变能释放率的影响

图4为SiC/316L不锈钢光滑基底系统中裂纹长度对应变能释放率的影响。当裂纹由萌生到开始扩展时，应变能释放率增长较快。随着裂纹长度的增加，应变能释放率的增长速率逐渐降低，随后保持为较为稳定的状态。当裂纹逐渐接近涂层与基底之间的交界面时，应变能释放率呈现出降低的趋势。以上结果表明，小裂纹对应变能释放率有着明显的影响。随着裂纹尖端逐渐靠近交界面，裂纹之间的相互作用以及应力强度因子对应变能释放率的影响逐渐增大，这将会导致应变能释放率的降低。

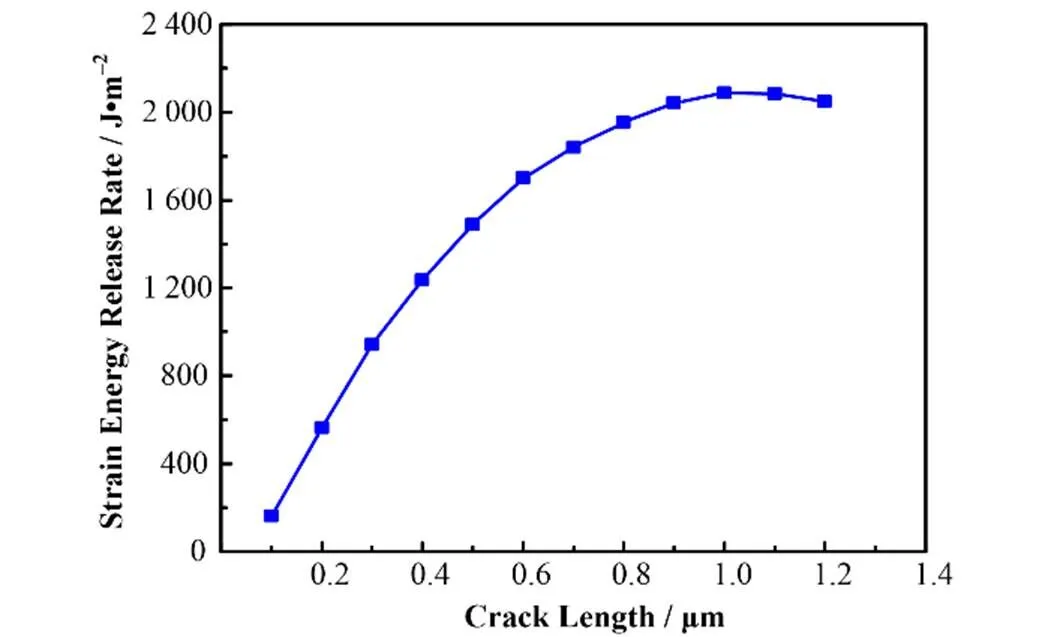
图4　表面裂纹长度对具有光滑基底表面的SiC/316L不锈钢系统应变能释放率的影响

如图5所示，为粗糙基底系统中裂纹的不同位置和长度对应变能释放率的影响。由图5可以看出，当裂纹处于不同位置时，应变能释放率均随着裂纹长度的增加而增加，随后均表现出降低的趋势。裂纹位于波峰时，应变能释放率最大，且增长速度较为明显。当裂纹位于波谷正上方时，应变能释放率增长速度最低。这是由于当裂纹位于波峰正上方时，具有较低刚度的316L不锈钢基底延伸到了较硬的SiC涂层中。延伸到SiC涂层中的这部分316L不锈钢仅能承担周围材料转化来的小部分载荷。然而，薄且硬的SiC涂层承担了剩余的大部分载荷，这将会显著增加裂纹尖端应力强度。因此，裂纹表现出了明显的扩展趋势。相反，当裂纹处于波谷位置时，316L不锈钢承担了大部分的载荷，而SiC涂层仅承担了剩余的小部分载荷。这将降低SiC涂层中裂纹尖端的应力强度，因此裂纹表现出了较低的扩展趋势。

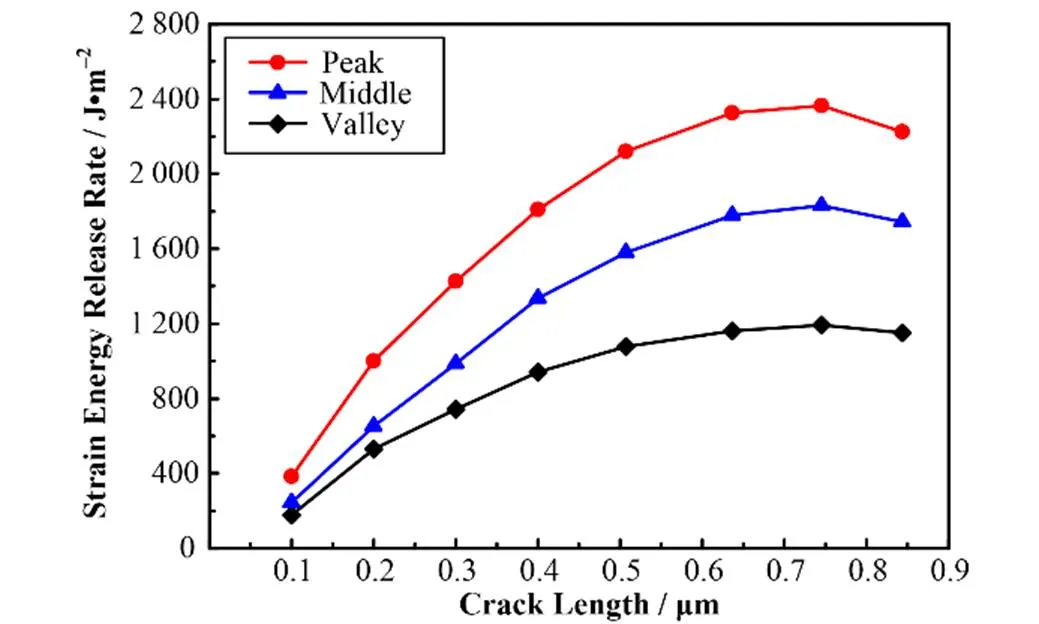
图5　在具有粗糙基底的SiC/316L不1锈钢系统中，裂纹位置和应变能释放率的关系

图6为基底表面振幅对应变能释放率的影响。由图6可见，基底表面波峰区域提高了应变能释放率，而波谷区域降低了应变能释放率。随着基底表面振幅的增加，这种现象变得更为明显。

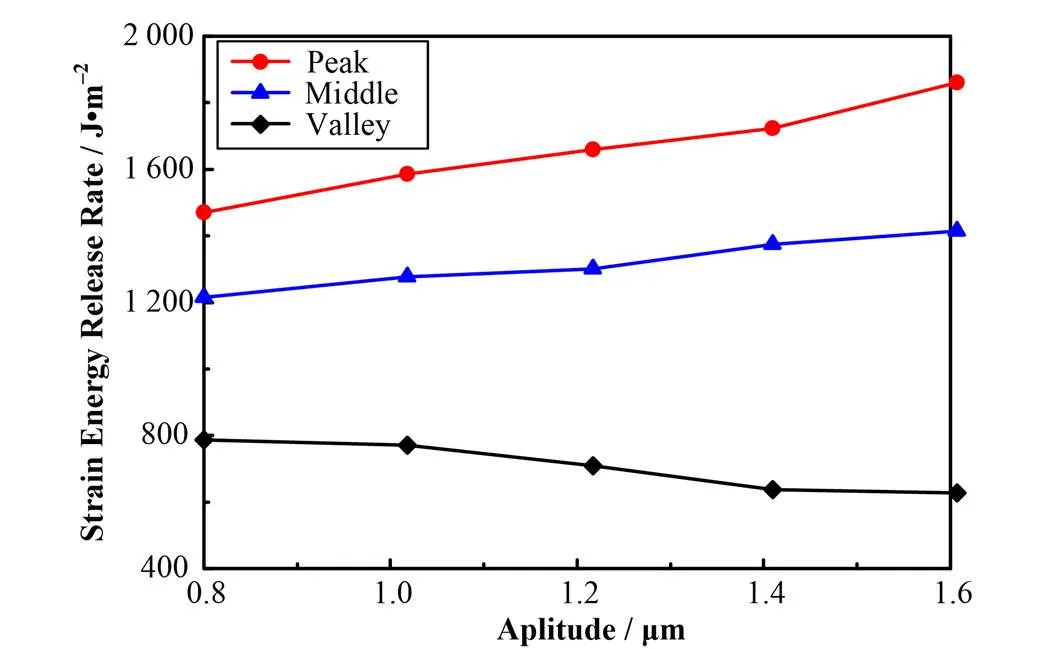
图6　基底表面振幅对应变能释放率的影响

2.2　粗糙基底表面对交界面应力的影响

当涂层系统服役过程中，受到外加载荷的作用时，由于涂层和基底材料机械性质的差异，会导致交界面区域出现应力集中，这可能会造成涂层脱落。而沿着交界面的应力分布是决定涂层结合强度的关键［16‒17］。因此，有必要对此部分进行深入分析。如图7～9所示，为裂纹分布于波峰、中间和波谷正上方位置时，沿着交界面路径的应力分布，以及与其对应于的光滑交界面的应力分布。可见，粗糙的基底表面对应力分布有着明显的影响。粗糙基底的引入，使沿着交界面的应力均有所降低。这是由于基底粗糙度导致界面应力受到了一定程度的抑制，进而减小了交界面的应力值。应力值的降低，有利于避免涂层从基底表面剥离。

图7　表面多重裂纹位于不同位置时，沿着交界面路径的应力分布情况 (a) 波峰，(b) 光滑

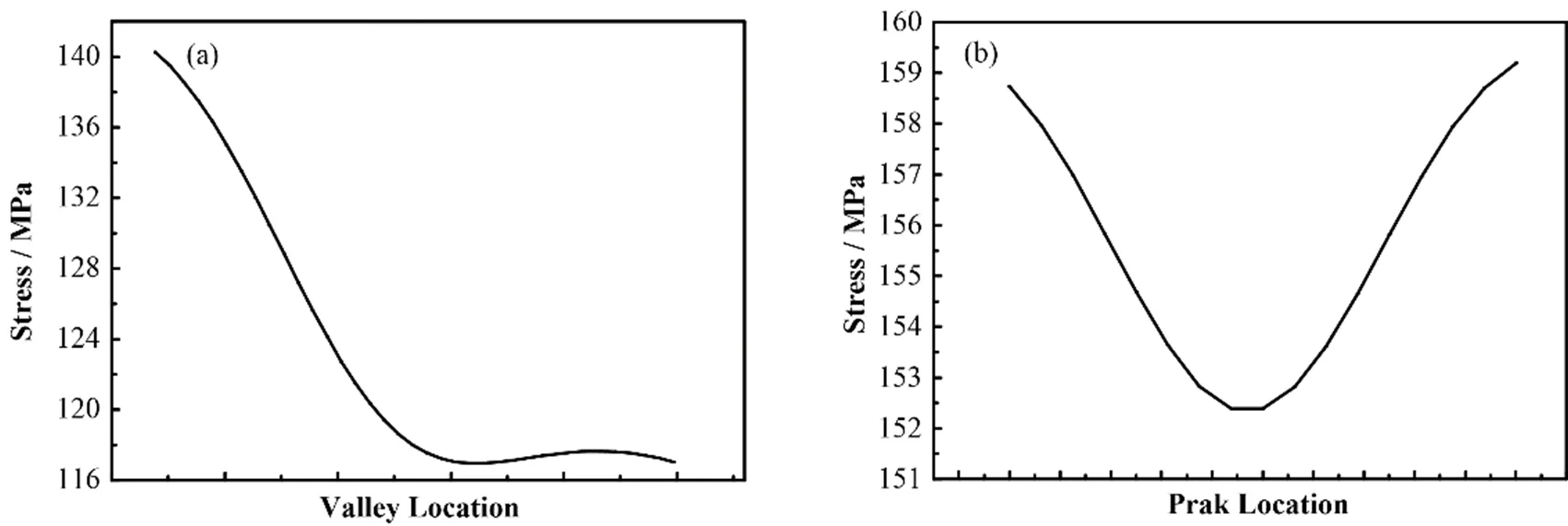
图8　表面多重裂纹位于不同位置时，沿着交界面路径的应力分布情况 (a) 中间，(b) 光滑

图9　表面多重裂纹位于不同位置时，沿着交界面路径的应力分布情况 (a) 波谷，(b) 光滑

如图10所示，为裂纹处于不同位置时的应力分布云图。从图10可以看出，当裂纹位于基底表面波峰正上方时应力值最大。当裂纹位于波谷正上方时对应的应力值最小。这是由于基底表面处于凸出情况下，SiC薄膜承担了大部分的应力。因此，涂层展现出较大的应力，裂纹在此情况下更容易扩展。

图10　在SiC/316L不锈钢系统中，裂纹位于不同位置时的应力分布 (a) 波峰，(b) 中间，(c) 波谷

3 结语

本文对SiC/316L不锈钢系统中涂层表面裂纹的性质进行了模拟研究，并且在研究过程中引入了基底粗糙度的影响。研究结果有助于理解SiC阻氚涂层表面裂纹应变能释放率、应力分布与基底粗糙度之间的关系，结论如下：

1）基底粗糙度对涂层表面裂纹的扩展有显著影响。当裂纹位于波峰时，应变能释放率最大，且增长速度较为明显。当裂纹位于波谷正上方时，应变能释放率增长速度最低。并且随着基底表面振幅的增加，这种现象变得更为明显。

2）基底表面粗糙度的引入可以一定程度地抑制沿着交界面路径的应力，使交界面的应力值有所降低。

3）当裂纹位于基底表面波峰正上方时，应力值最大，裂纹容易发生扩展。当裂纹位于波谷正上方时，对应的应力值最小，裂纹驱动力较低。

作者贡献声明 刘泽：酝酿和设计实验；唐琳：采集数据；孙付春：实施研究；张亚飞：实施研究；余松科：分析数据；母学玲：对文章的知识性内容作批评性审阅。

1 Levchuk D, Koch F, Maier H,. Deuterium permeation through eurofer and α-alumina coated eurofer[J]. Journal of Nuclear Materials, 2004, 328(2–3): 103–106. DOI: 10.1016/j.jnucmat.2004.03.008.

2 Hutchinson J W, Suo Z. Mixed mode cracking in layered materials[J]. Advances in Applied Mechanics, 1991, 29: 63–191. DOI: 10.1016/S0065-2156(08)70164-9.

3 Kawasaki A, Watanabe R. Thermal fracture behavior of metal/ceramic functionally graded materials[J]. Engineering Fracture Mechanics, 2002, 69(14–16): 1713–1728. DOI: 10.1016/S0013-7944(02)00054-1.

4 Erdogan F, Wu B H. Crack problems in FGM layers under thermal stresses[J]. Journal of Thermal Stresses, 1996, 19(3): 237–265. DOI: 10.1080/01495739608946172.

5 Choules B D, Kokini K, Taylor T A. Thermal fracture of ceramic thermal barrier coatings under high heat flux with time-dependent behavior: Part 1. Experimental results[J]. Materials Science and Engineering: A, 2001, 299(1–2): 296–304. DOI: 10.1016/S0921-5093(00)01393-9.

6 Liu Z, Yu G G, He A P,. Simulation of thermal stress in Er2O3and Al2O3tritium penetration barriers by finite-element analysis[J]. Plasma Science and Technology, 2017, 19(9): 095602. DOI: 10.1088/2058-6272/aa719d.

7 Liu Z, Meng F, Yi L B. Simulation of the effects of different substrates, temperature, and substrate roughness on the mechanical properties of Al2O3coating as tritium penetration barrier[J]. Nuclear Science and Techniques, 2019, 30(4): 62. DOI: 10.1007/s41365-019-0587-1.

8 Belytschko T, Black T. Elastic crack growth in finite elements with minimal remeshing[J]. International Journal for Numerical Methods in Engineering, 1999, 45(5): 601–620. DOI: 10.1002/(SICI)1097-0207(19990620)45: 5<601: AID-NME598>3.0.CO;2-S.

9 Zi G, Belytschko T. New crack-tip elements for XFEM and applications to cohesive cracks[J]. International Journal for Numerical Methods in Engineering, 2003, 57(15): 2221–2240. DOI: 10.1002/nme.849.

10 Chessa J, Smolinski P, Belytschko T. The extended finite element method (XFEM) for solidification problems[J]. International Journal for Numerical Methods in Engineering, 2002, 53(8): 1959–1977. DOI: 10.1002/nme.386.

11 Cheng K W, Fries T P. Higher-order XFEM for curved strong and weak discontinuities[J]. International Journal for Numerical Methods in Engineering, 2010, 82(5): 564–590. DOI: 10.1002/nme.2768.

12 Benson D J, Bazilevs Y, de Luycker E,. A generalized finite element formulation for arbitrary basis functions: from isogeometric analysis to XFEM[J]. International Journal for Numerical Methods in Engineering, 2010, 83(6): 765–785. DOI: 10.1002/nme.2864.

13 Zhang W X, Wang T J, Li L X. Numerical analysis of the transverse strengthening behavior of fiber-reinforced metal matrix composites[J]. Computational Materials Science, 2007, 39(3): 684–696. DOI: 10.1016/j.commatsci.2006.08.023.

14 Liu H B, Tao J, Gautreau Y,. Simulation of thermal stresses in SiC-Al2O3composite tritium penetration barrier by finite-element analysis[J]. Materials & Design, 2009, 30(8): 2785–2790. DOI: 10.1016/j.matdes.2009. 01.025.

15 Grujicic M, Zhao H. Optimization of 316 stainless steel/alumina functionally graded material for reduction of damage induced by thermal residual stresses[J]. Materials Science and Engineering: A, 1998, 252(1): 117–132. DOI: 10.1016/S0921-5093(98)00618-2.

16 刘红兵, 陶杰, 张平则, 等. 316L不锈钢基材功能梯度Al涂层残余热应力分析[J]. 核技术, 2008, 31(2): 105–110.

LIU Hongbing, TAO Jie, ZHANG Pingze,. Stimulation of residual stresses in functionally gradient Al coatings on 316L substrate[J]. Nuclear Techniques, 2008, 31(2): 105–110.

17 尹磊, 陶杰, 苏新清, 等. 双层辉光离子渗金属技术制备Al-Cr-Si氧化物阻氚涂层[J]. 核技术, 2010, 33(10): 765–770.

YIN Lei, TAO Jie, SU Xinqing,. Preparation of Al-Cr-Si oxide tritium permeation barrier by double glow plasma technology[J]. Nuclear Techniques, 2010, 33(10): 765–770.

Performance of cracks on the surface of SiC tritium penetration barrier based on Abaqus

LIU Ze1TANG Lin1SUN Fuchun2ZHANG Yafei1YU Songke1MU Xueling1

1()2()

During the service period of the tritium barrier coating in the fusion reactor, the crack performance of the coating surface and the roughness of the substrate are the key factors restricting the service cycle of the coating.This study aims to clarify the relationship between substrate roughness and coating surface cracks in SiC/316L stainless steel tritium barrier coating system. [Method] Based on the Abaqus finite element software, SiC/316L stainless steel tritium penetration barrier system was established. Factors such as the strain energy release rate, amplitude of substrate and length position were investigated with emphasis on the relationship between substrate roughness and coating surface cracks.The results show that the substrate roughness has a significant effect on the strain energy release rate of the coating surface cracks. When the crack is above the peak of the substrate, the strain energy release rate is the largest. When the crack is located directly above the valley, the strain energy release rate is the smallest. Compared with the smooth interface, the stress along the rough interface is suppressed, showing a decreasing trend.This study reveals the influence of crack position on the driving force of crack growth.

SiC tritium penetration barrier, Multiple cracks on the surface, Strain energy release rate, Stress

LIU Ze, male, born in 1986, graduated from Sichuan University with a doctoral degree in 2019, focusing on nuclear material design

2021-12-13,

2022-03-02

TL99

10.11889/j.0253-3219.2022.hjs.45.060202

刘泽，男，1986出生，2019年于四川大学获博士学位，研究领域为反应堆结构材料

2021-12-13，

2022-03-02