双驱动补偿压弯的椭圆镜有限元分析
2022-06-27马天宇卢启鹏王大壮彭忠琦龚学鹏宋源
马天宇 卢启鹏 王大壮 彭忠琦 龚学鹏 宋源
双驱动补偿压弯的椭圆镜有限元分析
马天宇1,2卢启鹏1王大壮1彭忠琦1龚学鹏1宋源1
1(中国科学院长春光学精密机械与物理研究所应用光学国家重点实验室 长春 130033)2(中国科学院大学 北京 100049)
为满足同步辐射光束线对相关光学元件的技术需求,设计了双驱动四点滚柱压弯机构。通过有限元仿真分析实现高精度大尺寸光学镜面的非等力矩椭圆柱面压弯。以外形尺寸为1 200 mm×70 mm×50 mm的反射镜为研究对象,基于物距26.5 m、像距13 m及掠入射角2.8 mrad,根据理论椭圆面形方程与梁变形弯矩方程计算出施加在压弯镜两端的不等力矩。利用有限元软件对双驱动四点压弯机构进行仿真分析,在重力补偿力矩存在情况下,分别对聚焦镜进行单点补偿、双点补偿、三点补偿以及四点补偿的有限元分析,得到与理论计算相对应的仿真补偿面形结果。模拟施加两端的不等力矩将面形误差从单点补偿时的0.81 µrad降低到四点补偿下的0.075 µrad,对应理论面形误差0.013 µrad,最大程度可以降低原误差的95.96%,证实四点式双驱动机构通过多点补偿可以对椭圆压弯面形误差产生有效减小的趋势,且减小趋势不断平缓。证明该机构在多点补偿下对大尺寸椭圆镜压弯精度的提高具有可行性和有效性,对同步辐射光束线压弯技术有重要的理论指导作用与意义。
压弯机构,椭圆柱面,有限元分析,面形误差,同步辐射
同步辐射光源是涉及众多研究领域的综合性科学装置。同步辐射光由储存环发出,经过光束线的聚焦、准直、偏转、分光等一系列处理形成特定光束服务于相应的实验站[1]。作为一种亮度高、能量强、时间脉冲好的洁净光源,同步辐射在众多高精尖学科领域发挥着重要作用,取得了令人瞩目的创新性科研成果。
在同步辐射光束线上,聚焦反射镜的应用场合居多,由于掠入射角的减小,只能通过增大聚焦反射镜的自身长度满足光束线的技术需求。伴随着光学元件尺寸的增加,针对各种面形的大尺寸光学元件加工难度不断增大,无法保证足够的面形精度。因此,利用压弯机构将平面镜或柱面镜压弯成光束线所需形状的反射镜,成为现阶段同步辐射光束线领域的重要技术手段与研究内容。压弯机构可以分为压电压弯、仿形压弯与机械压弯[2]。以机械压弯为主,采用三点压弯、四点压弯、双臂压弯以及柔性铰链压弯等方式[3],压弯机构易加工、可装调,通过调节光学元件的曲率半径来满足光束线对光学元件的面形需求。
相较于圆柱面镜,非圆柱面的曲率半径是连续变化的,其中的椭圆柱面镜可以通过单点对单点的聚焦提升反射镜的聚焦能力。与此同时,通过调节椭圆面形的压弯程度来满足变化的物距、像距以及掠入射角,从而实现调焦的能力。在大尺寸光学元件对应的压弯椭圆柱面镜中,压弯机构可以有效减小掠入射角的指标,在一定程度上减小聚焦反射镜对入射同步辐射光的损耗,增加像中心光子通量密度,进一步提升了同步辐射光的应用指标。
目前有两种方式可以将聚焦反射镜压弯成椭圆柱面镜,一种是变截面宽度镜子等力矩压弯[4‒5],另一种是等截面宽度镜子非等力矩压弯。变截面宽度的镜子在长度方向上的宽度值是连续变化的。对于面形精度的需要使其加工难度较大,制造成本较高,而且在调整镜面压弯曲率半径时不能满足可能需要变化的椭圆面形参数,降低了该压弯方式的实际应用效果。基于等宽度非等力矩压弯镜则是利用机械压弯结构在镜子两端施加不等力矩即可得到原理误差很小的椭圆面形。聚焦镜重力载荷对压弯面形精度产生很大影响,目前通过补偿装置能够降低面形误差,通过结合多点驱动补偿与力矩补偿的方式减轻重力面形影响,得到多点补偿下的椭圆压弯面形结果,进而探究满足工程指标需求的高精度椭圆镜面形。英国钻石光源(Diamond Light Source)通过双驱动机构将变截面镜压弯成面形误差为0.2 µrad的椭圆柱面镜[6];同样,法国SOLEIL同步辐射光源通过柔性铰链机构将1.1 m的变截面镜压弯成椭圆柱面镜,其面形误差为0.28 µrad[7]。在国内,上海光源对同步辐射压弯技术有深入研究,通过千斤顶式压弯机构对1 m的平面镜进行压弯,获得面形误差为0.8 µrad的圆柱面形;通过拉杆式压弯机构将1 m长的等宽度聚焦镜压弯成椭圆柱面镜,面形误差为0.5 µrad[7]。本文在单杆驱动等力矩压弯的基础上,设计出一种双杆驱动非等力矩的四点滚柱压弯结构装置,该结构通过固定挡板隔离两端驱动装置,凭借步进电机独立调控驱动位移。该结构与压弯镜的夹持方式采用线面接触,相较于U形压弯机构,在驱动过程中降低了自身对镜子端部的夹持影响,从而保证在调节压弯镜力矩时可以得到高精度的椭圆面形。
该结构压弯变形的整体优势包括:装调方便,两端通过内部滚珠丝杠独立输出驱动位移,可精准调控压弯力矩;通过压辊,固定辊与光学元件进行四点接触,使光学元件在压弯变形方向上不受机构自身重力影响;同时,在其他方向上通过点面接触限制其自由度,在很大程度上降低了夹持力对压弯面形的影响。该压弯镜机构可有效弥补其他机构对等截面椭圆柱面镜的压弯缺陷,提高压弯面形精度。
本文应用双驱动四点滚柱压弯机构对1.2 m等截面宽度镜子进行压弯,通过非等力矩输出获得椭圆面形压弯。将梁的非等力矩压弯公式与椭圆斜率方程结合得到对应的压弯力矩;通过有限元分析对四点双驱动机构和压弯镜进行静力学仿真,在重力影响下通过力矩补偿与补偿机构相结合的方式分别进行无补偿压弯、单点补偿压弯、双点补偿压弯,三点补偿压弯以及四点补偿压弯;对多点重力补偿的椭圆镜压弯面形进行有限元分析,得到对应的仿真施加力矩以及椭圆面形误差。
1 椭圆柱面镜压弯理论分析
1.1 压弯原理
如图1所示,以镜子中心作为原点建立坐标系,通过施加在镜子两端的非对称力矩1、2将其压弯成椭圆柱面镜,1和2为椭圆压弯镜的曲率半径。根据工程力学中梁变形的计算公式求取对应镜子的压弯力矩如下:
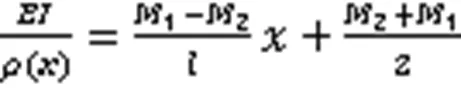

式中:为镜子的弹性模量;是镜子截面对中心的惯性矩;()为镜子弯曲之后对应点的曲率半径。将()近似为″()的倒数代入式(1)中,可以得到式(2),对式(2)积分可得变形曲线斜率方程的二阶公式[7‒8],即为式(3):

1.2 椭圆柱面镜理论面形计算
椭圆镜聚焦光路如图2所示。由图2中几何关系可得出椭圆面形关于、以及的表达式,(1)与(2)为椭圆焦点。在图2坐标系下椭圆长短轴、可以具体表达为:

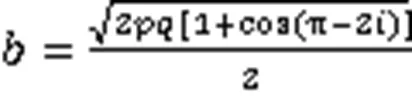
将式(4)和(5)代入椭圆斜率方程中,可以得出具体参数表达的斜率方程,如式(6):

在束线光学中,镜面的斜率误差一般作为衡量面形误差的指标。通过计算压弯镜面形上各点斜率和理论面形对应点的斜率做差值得出斜率残差,以斜率残差的均方根值作为评价压弯镜面形误差的指标[9]。计算公式如下:
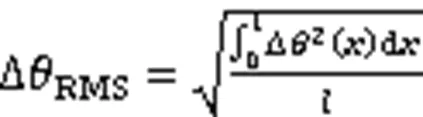


表1 聚焦反射镜技术指标
1.3 双驱动四点压弯机构
压弯机构在光束线中是实现光学元件压弯成形的核心部分,整体机构性能也是评价压弯镜面形的重要参考指标[10]。目前压弯机构的种类有很多,以机械压弯为主大致分为四点压弯和柔性铰链压弯[11]。本文是以千斤顶式的双驱动四点压弯机构为研究对象,实现椭圆柱面镜的压弯。四点压弯机构通过上下滚柱的相对位置对镜子产生压弯力矩,稳定性较强,而且对镜子两端夹持力小,压弯面形的精度较高。四点压弯机构在机械压弯中实用性很强,被广泛应用于同步辐射光束线中。图3为双驱动四点压弯机构具体的三维模型图。图4为压弯机构的侧视图,其中,A为固定辊,主要起支撑作用;B为压辊,主要对镜子进行压弯;C为固定元件,限制镜子在压弯过程中的自由度;D为限位元件,对镜子起到固定作用。
该双驱动四点滚柱压弯机构以四点压弯为设计依据,利用压辊与镜子的线面接触,既保证稳定性的同时又避免夹持力对镜子的影响,提高了整体压弯面形精度。其工作原理是通过电机驱动两侧驱动杆,使驱动力作用在与摇臂连接的动力轴上。随着摇臂相对于底座发生转动使压辊与镜子工作面发生接触,由于固定辊的支撑使镜子两端产生压弯力矩。其中固定辊与底座和压辊与摇臂均通过轴承连接,固定辊、压辊与镜面发生滚动接触防止摩擦力过大。通过中间挡板分离两个驱动机构,独立控制两个驱动机构输出不同的力,从而产生非等力矩,进而实现大尺寸椭圆柱面镜的压弯成形。

图3 双驱动四点压弯机构三维模型图

图4 压弯机构侧视图
2 椭圆柱面镜压弯有限元分析
2.1 有限元设计
有限元分析的过程包括通过对压弯机构以及压弯镜进行简易模型建立;对模型的材料参数进行设定;进行适当的网格划分,施加相应的载荷和约束,从而得到镜子模拟的变形结果[12];最后计算出镜面的均方根斜率误差,验证之前的理论计算和分析。有限元相关应用场景有很多,主要针对静力学、动力学、流体力学以及电磁场等物理方面的场景研究。本文主要应用静力学有限元分析。
镜子选用材料硅,动力轴选用轴承钢,其他部件选用不锈钢,不同材料属性如表2所示。分别添加模型材料后,对镜子以及接触的压辊和固定辊进行适当的网格划分,考虑到精度需求以及时间成本选取5 mm的六面体网格对模型细化。
对模型进行边界条件设置,动力轴与摇臂之间采用粘合接触(Bonded),其他接触面均采用摩擦接触(Frictional)。在最大可能模拟实际场景的前提下,同时也要保证仿真结构的结果收敛,对不同接触面的摩擦系数需要进行适当改变[13]。其中摇臂与底座的轴孔接触面考虑到真实场景是轴承接触,转动的摩擦力非常小,所以将此处的摩擦系数设置为0.01。压辊、固定辊与镜子的接触面是仿真的核心接触面,通过调试发现,摩擦系数设置为0.15为最优。其次为保证辊子在镜面上发生滚动时摩擦力较小,且考虑整体模型的非线性,包括固定辊、压辊与底座,摇臂轴孔接触面摩擦系数也选取0.15。除此之外,还要针对辊子的结构特征适当添加转动副,对从动件的固定辊转动面设为自转转动副,对主动件的压辊和摇臂转动面设置为作用面对目标面的转动副。最后对两端底座设置固定约束,除压弯变形方向外限制其他自由度。对模型施加不等力矩开始调试仿真,仿真结果选择中心曲线获取拟合[14]。

表2 模型材料属性
双驱动四点压弯机构经驱动压弯后得到整体的变形云图如图5所示,随着对两端动力轴分别输入非等驱动力1、2,摇臂发生相对转动,与摇臂垂直方向产生实际压弯力1、f,实际压弯力与摇臂的乘积就是输出力矩。通过拟合得到理想状态下的压弯力矩分别为20.11 N·m,21.60 N·m,与理论计算力矩19.09 N·m,20.49 N·m对比大小较为吻合。图6为压弯镜仿真变形云图。图5、图6均对应的是无重力存在时理想状态下的椭圆面形仿真。

图5 压弯机构仿真变形图
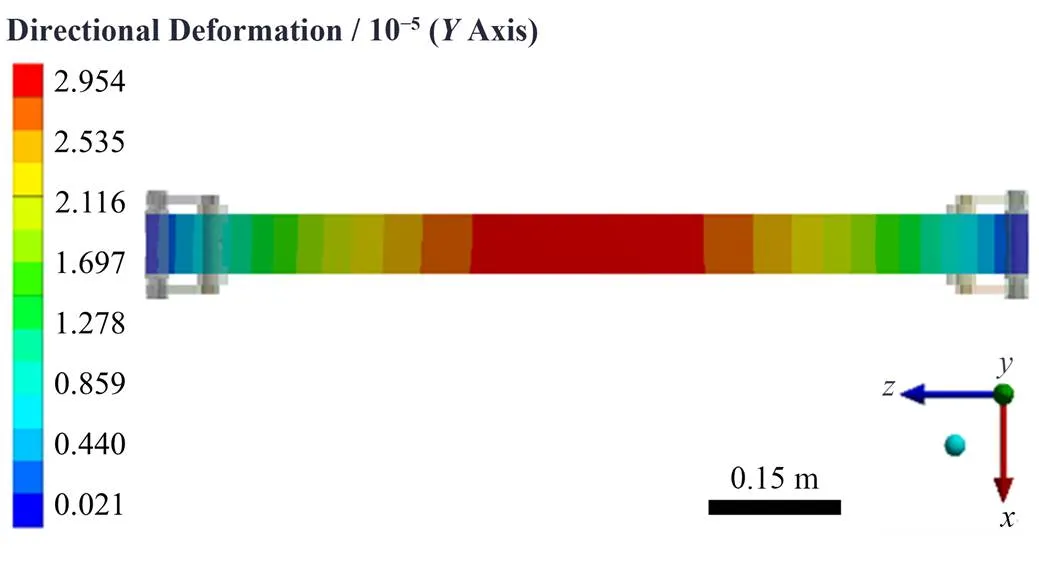
图6 压弯镜仿真变形图
2.2 多点重力补偿仿真调试
同步辐射光束线应用的大尺寸椭圆聚焦反射镜是处于镜箱封闭的真空环境当中,受重力影响,压弯镜面形精度下降很多[15]。通过补偿装置建立压弯镜的补偿点可以有效降低受重力影响的面形误差。当点数越多,面形误差在原理上下降的趋势越明显,通过镜子两端补偿力矩可以在补偿面形的基础之上再次降低面形误差[16],得到相对更加接近平面的补偿面形。在这种状态下再通过增大两端力矩,实现非等力矩椭圆压弯。此时影响面形误差的因素可以归纳为三个,分别为原理误差、双驱动四点压弯机构的系统误差以及重力补偿的残余误差。除了原理误差没有改变,通过夹持力影响较小的双驱动四点压弯机构和补偿点结合补偿力矩的方式共同降低重力影响的面形误差,在整体上可以降低椭圆镜的压弯面形误差,提高面形聚焦精度。图7为镜子自身重力变形仿真结果,经计算为16.12 µrad。

图7 镜子重力变形仿真
设置多点补偿的结构方式,在原理上可以有效减小重力对镜子面形影响,对应最优的面形补偿结果可以计算出最佳补偿点的位置和最佳补偿力的大小。根据压弯镜的尺寸计算相应理论的多点补偿面形误差,参数代入有限元分析。如图8(a)所示,1、2分别为有效压弯力,此时保持相等以施加等力矩。单点补偿时,Support 1大小为47.462 N,补偿力矩为2.647 N·m,面形误差为0.822 µrad;双点补偿时如图8(b)所示,1为0.371 m,Support 1和Support 2大小均为29.634 N,补偿力矩为1.611 N·m,对应的面形误差为0.224 µrad;三点补偿时如图8(c)所示,Support 1大小为22.729 N,1为0.569 m,Support 2和Support 3大小均为22.537 N,补偿力矩为1.036 N·m,面形误差为0.098 µrad;四点补偿时如图8(d)所示,1为0.233 m,Support 1和Support 2大小均为18.509 N,2为0.689 m,Support 3和Support 4大小均为18.317 N,补偿力矩为0.575 N·m,面形误差为0.06 µrad。整个多点补偿的面形误差对比如图9所示,可以得出仿真结果的面形误差随着多点补偿的相应点数增加产生减小趋势[17]。如图10所示,左侧为在补偿力矩存在情况下随着补偿点数增加,理论计算面形误差的变化趋势,右侧为相对应的仿真计算面形误差变化趋势,二者趋势相近。单点补偿误差可以达到未补偿时的94.9%,随着点数的增加,效果不断优化,可以得出多点补偿的效果是十分明显的。

图8 多点重力补偿的压弯原理图
(a) 单点补偿压弯原理,(b) 双点补偿压弯原理,(c) 三点补偿压弯原理,(d) 四点补偿压弯原理
Fig.8Schematic diagram of multipoint bending with gravity compensation
(a) Principle of single-point compensation bending, (b) Principle of two-point compensation bending, (c) Three-point compensation bending principle, (d) Four-point compensation bending principle

图9 多点补偿的斜率误差对比

图10 重力补偿面形误差随补偿点变化趋势
2.3 多点补偿压弯调试
当椭圆压弯反射镜面朝向方向与重力方向相同时,通过施加的力矩可以抵消部分重力影响,减小补偿装置对镜子产生的额外补偿力,在一定程度上降低镜子的使用风险。图8中为镜子重力载荷79.919 N·m-1,为镜子长度1.2 m,为上下辊产生压弯力矩的有效距离。
如图11(a)所示,假设在无重力影响的理想状态下,对机构两端施加驱动得到压弯镜模拟面形,经计算此时的面形误差为0.058 µrad,该面形误差主要由理论物像距以及掠入射角参数来决定,其次由压弯机构的系统误差来决定。该面形误差与理论计算面形误差0.013 µrad相差不大,可以认定双驱动四点机构对椭圆压弯面形效果较好。其次,当重力影响存在时,在无重力补偿装置的前提下,仅通过力矩补偿聚焦镜自身重力影响从而进行压弯,可得到最后的椭圆面形误差为1.858 µrad,如图11(b)所示。相较于聚焦镜水平偏转[18],在垂直偏转的情况下,重力不仅对聚焦镜母线变形影响较大,而且对整个面形都有很大影响,造成聚焦后的光斑尺寸偏大,所以需要进行多点重力补偿调试。在镜子中心进行单点补偿的情况下,再驱动力矩进行压弯得到最后的椭圆面形误差为0.81 µrad,如图11(c)所示。随后分别进行双点补偿重力压弯、三点补偿重力压弯及四点补偿重力压弯,分别对应图11(d)、(e)和(f),得到椭圆压弯面形误差为0.25 µrad、0.105 µrad和0.075 µrad。根据有限元计算证明在理论误差较小的情况下,通过多点补偿和力矩补偿可以在很大程度上降低重力对压弯面形的影响,得到面形误差较小的椭圆压弯面形。

图11 多点补偿的椭圆压弯面形误差仿真对比
(a) 无重力理想压弯,(b) 无补偿压弯,(c) 单点补偿压弯,(d) 双点补偿压弯,(e) 三点补偿压弯,(f) 四点补偿压弯
Fig.11Simulation comparison of elliptic bending surface shape error with multi-point compensation
(a) Ideal bending with No gravity, (b) Uncompensated bending, (c) Single point compensation bending, (d) Double point compensation bending, (e) Double point compensation bending, (f) Double point compensation bending
如表3所示,随着补偿点数的增加,驱动力矩1由33.47 N·m降低为22.91 N·m,力矩2由35.02 N·m降低为24.29 N·m;对应的驱动杆位移1由53.52 µm降低为42.28 µm,2由55.33 µm降低为43.90 µm,驱动位移的变化趋势与力矩一致。当重力方向与力矩施加方向相反时可以通过增加两端的力矩来减小重力影响的面形误差,调试非等力矩的过程中发现随着补偿点数的增加,两端驱动的不等力矩也逐渐减小,由于补偿点数的增加,补偿装置的补偿效果逐步增大,驱动力矩的补偿效果就有所减小,因此造成不等驱动力矩的下降趋势。

表3 多点补偿的仿真力矩与位移
针对同步辐射光束线应用的大尺寸光学元件压弯面形,曲率可以反映真实的镜面面形。理想的椭圆面形曲率是随着自身尺寸的增加而不断变化的,通过计算可以得出拟合的椭圆曲率变化情况。随着补偿点数的增加,补偿效果不断优化,对应的压弯曲率也与理论的相对差值不断减小,变化趋势随着补偿力度的增加逐渐接近理论椭圆曲率。图12为多点补偿压弯的椭圆曲率对比。由图12可知,多点补偿压弯后的椭圆曲率相对于理论椭圆曲率的差值可以较为直观地观察,在补偿点数增加的情况下,曲率差值逐渐趋近于0,且压弯后的曲率差值沿着镜子长度方向均匀对称分布,同时整条差值曲线界于0的上下区间,在拟合过程中经调试后的压弯曲率与理论曲率对称相交,证明压弯面形与理论面形最大程度拟合。单点补偿压弯的镜面中心曲率误差为4.33×10-6,四点补偿压弯的镜面中心曲率误差为2.63×10-7,由单点补偿到四点补偿椭圆压弯中心曲率精度提升1个数量级。图13为多点补偿的椭圆压弯面形的矢量高度误差对比。

图12 多点补偿压弯的椭圆曲率及其差值对比 (a) 多点补偿的椭圆曲率,(b) 多点补偿的曲率误差
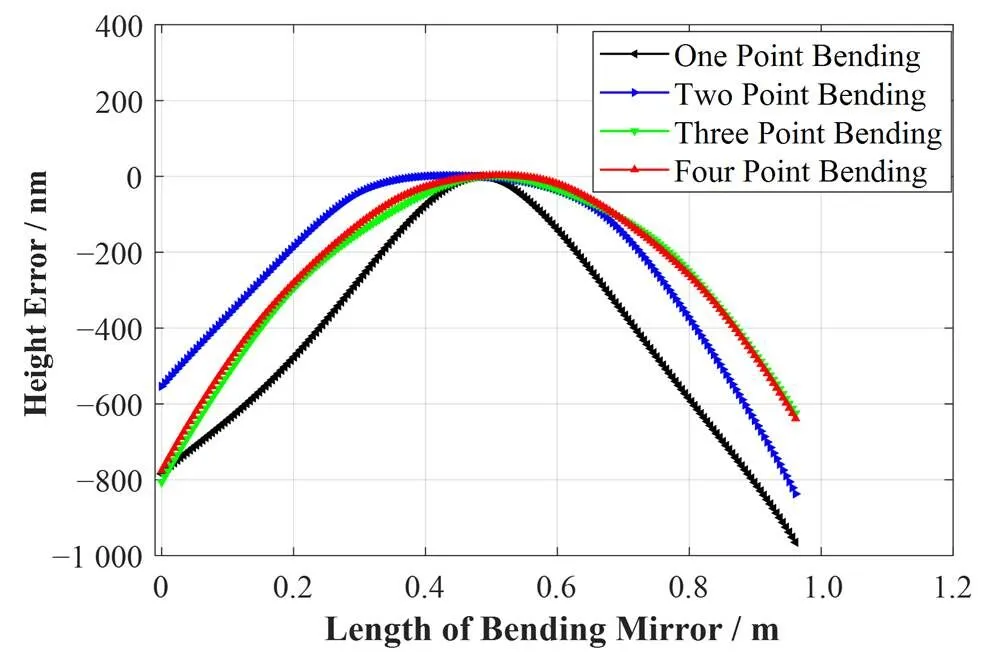
图13 多点补偿的椭圆矢高误差对比
由图14可知,椭圆面形压弯误差随着补偿点数的增加而逐渐减小,但减小趋势逐渐放缓。当单点补偿时,椭圆压弯面形相对于无补偿压弯整整降低了原面形误差的56.41%,补偿效果显著,之后随着补偿点数的增加,椭圆压弯面形误差降低趋势逐渐减缓,双点补偿的椭圆面形误差相较于无补偿压弯降低86.53%,三点补偿压弯相较于无补偿压弯降低94.35%,四点补偿压弯相较于无补偿压弯降低95.96%。在实际测量环境中,随着多点重力补偿的进行,椭圆压弯面形受重力影响逐渐消除,其自身面形误差的影响占比不断增大。通常自身面形误差越小,多点补偿压弯镜面形误差的下降趋势越明显。

图14 椭圆面形误差随补偿点数的变化趋势
3 结语
大尺寸椭圆柱面聚焦镜可以通过选取对应的物距像距以及掠入射角参数,在镜子两端施加不等力矩来获取。基于1 200 mm×70 mm×50 mm尺寸的镜子为研究对象,通过双驱动四点压弯机构实现非等力矩椭圆面形压弯,在有限元分析的基础上校验多点补偿的椭圆压弯面形变化。由于镜子自身重力影响导致椭圆面形压弯误差偏大,增设补偿装置模拟多点重力补偿,仿真计算的结果验证通过机构两端的力矩补偿和补偿装置的多点补偿可以有效降低重力影响的面形误差,达到进一步降低面形误差的目的。得到与理论补偿计算相对应的仿真结果,由单点补偿的面形误差0.822 µrad下降到四点补偿的面形误差0.062 µrad。不断调整压弯力矩,使得与理想椭圆相比面形误差最小。随着增设补偿的补偿效果不断优化,压弯的椭圆面形误差逐渐减小,且减小趋势由明显趋于平缓。在物像比和掠入射角一定的情况下,椭圆面形误差由单点补偿压弯的0.81 µrad降低到四点补偿压弯的0.075 µrad,由降低原面形误差的56.41%上升到95.96%,验证了多点补偿压弯镜自身重力对压弯椭圆面形误差降低的有效性。在三点补偿下,相较于拉杆式机构驱动的椭圆镜压弯,面形误差由0.45 µrad提升至0.105 µrad,证明通过双驱动四点滚柱压弯机构对进一步提高椭圆镜压弯精度具有研究价值和借鉴意义,同时对丰富和加强同步辐射光束线压弯技术具有理论指导作用。
致谢 在此感谢上海光源的王楠老师和任祖洋老师对论文思路的细心指导和帮助;同时感谢祝万钱老师的大力支持。
作者贡献声明 马天宇:负责本论文方案设计,数据整理分析,论文撰写和修改;卢启鹏:负责方案提出,论文写作与修改指导,研究经费的获取;王大壮:负责仿真数据的验算及分析;彭忠琦、龚学鹏和宋源:参与方案设计,结构论证,论文的修改。
1 曾昭权. 同步辐射光源及其应用研究综述[J]. 云南大学学报(自然科学版), 2008, 30(5): 477–483, 488. DOI: 10.3321/j.issn:0258-7971.2008.05.009.
ZENG Zhaoquan. A Sum Mary of synchrotron radiation source and its application research[J]. Journal of Yunnan University (Natural Sciences Edition), 2008, 30(5): 477–483, 488. DOI: 10.3321/j.issn:0258-7971.2008.05.009.
2 金利民, 罗红心, 王劼, 等. 双压电片镜在同步辐射光源光学系统中的应用[J]. 中国光学, 2017, 10(6): 699–707. DOI: 10.3788/CO.20171006.0699.
JIN Limin, LUO Hongxin, WANG Jie,. Application of bimorph mirror in the optical system of synchrotron radiation light source[J]. Chinese Journal of Optics, 2017, 10(6): 699–707. DOI: 10.3788/CO.20171006.0699.
3 高飒飒. 同步辐射光束线水平偏转压弯机构关键技术研究及性能测试[D]. 长春: 中国科学院长春光学精密机械与物理研究所, 2014.
GAO Sasa. Key technology research and performance testing of horizontal deflection bender used in synchrotron radiation beamline[D]. Changchun: Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, 2014.
4 周博文, 王楠, 祝万钱, 等. 等截面反射镜椭圆压弯机构变像距压弯[J]. 中国光学, 2020, 13(4): 778–786. DOI: 10.37188/CO.2019-0250.
ZHOU Bowen, WANG Nan, ZHU Wanqian,. Variable image distance bending using an elliptical bending mechanism with a constant cross-section mirror[J]. Chinese Journal of Optics, 2020, 13(4): 778–786. DOI: 10.37188/CO.2019-0250.
5 毛成文, 余笑寒, 肖体乔. 变宽度压弯椭圆柱面聚焦镜的光学参数可调性[J]. 核技术, 2009, 32(5): 333–336.
MAO Chengwen, YU Xiaohan, XIAO Tiqiao. Tunability of optical parameters of width-variable bent elliptical microfocus mirror[J]. Nuclear Techniques, 2009, 32(5): 333–336.
6 Nistea I T, Alcock S G, Kristiansen P,. Long, elliptically bent, active X-ray mirrors with slope errors <200 nrad[J]. Journal of Synchrotron Radiation, 2017, 24(3): 615–621. DOI: 10.1107/s1600577517005422.
7 秦超. 同步辐射椭圆柱面压弯镜机构的研究[D]. 上海: 中国科学院上海应用物理研究所, 2018.
QIN Chao. Research on synchrotron radiation elliptic cylinder mirror bender[D]. Shanghai: Shanghai Institute of Applied Physics, Chinese Academy of Sciences, 2018.
8 Protopopov V V. Focusing of X-rays by flexible mirrors under arbitrary loading[J]. Optics Communications, 2001, 199(1–4): 1–15. DOI: 10.1016/S0030-4018(01)01482-1.
9 周平伟, 马宏财. 镜面面形误差统计方法研究[J]. 激光与光电子学进展, 2016, 53(4): 041201. DOI: 10.3788/LOP53.041201.
ZHOU Pingwei, MA Hongcai. Research of statistical methods for mirror surface figure error[J]. Laser & Optoelectronics Progress, 2016, 53(4): 041201. DOI: 10.3788/LOP53.041201.
10 卢启鹏, 彭忠琦. 压弯机构在同步辐射光束线中的应用[J]. 光机电信息, 2011, 28(6): 8–13. DOI: 10.3788/OMEI20112806.0008.
LU Qipeng, PENG Zhongqi. Application of bender in synchrotron radiation beamline[J]. Ome Information, 2011, 28(6): 8–13. DOI: 10.3788/OMEI20112806.0008.
11 程光宇, 黄智超, 王克逸, 等. 同步辐射聚焦镜压弯机构设计与面形误差分析[J]. 应用光学, 2019, 40(1): 120–126. DOI: 10.5768/JAO201940.0105003.
CHENG Guangyu, HUANG Zhichao, WANG Keyi,. Design and surface shape error analysis of synchronous radiation focusing mirror bending mechanism[J]. Journal of Applied Optics, 2019, 40(1): 120–126. DOI: 10.5768/JAO201940.0105003.
12 秦超, 薛松, 王楠, 等. 压弯椭圆柱面镜的有限元分析[J]. 核技术, 2018, 41(1): 010101. DOI: 10.11889/j.0253-3219.2018.hjs.41.010101.
QIN Chao, XUE Song, WANG Nan,. The finite element analysis of the bent elliptical cylindrical mirror[J]. Nuclear Techniques, 2018, 41(1): 010101. DOI: 10.11889/j.0253-3219.2018.hjs.41.010101.
13 Gong X P, Lu Q P, Wang Y,. Mechanical design and finite element analyses of surface bending mechanism for X-ray optics[J]. Precision Engineering, 2018, 53: 107–119. DOI: 10.1016/j.precisioneng.2018.03.005.
14 闫力松, 杨甬英, 马冬林, 等. 长条形镜面面形拟合技术研究[J]. 中国光学, 2018, 11(6): 1011–1016. DOI: 10.3788/CO.20181106.1011.
YAN Lisong, YANG Yongying, MA Donglin,. Surface fitting technology of rectangular mirror[J]. Chinese Journal of Optics, 2018, 11(6): 1011–1016. DOI: 10.3788/CO.20181106.1011.
15 周泗忠, 杨晓许, 时惠霞. 压弯聚焦镜自重的平衡[J]. 核技术, 2005, 28(3): 180–182.
ZHOU Sizhong, YANG Xiaoxu, SHI Huixia. Study of gravity compensation of bent focusing mirror[J]. Nuclear Techniques, 2005, 28(3): 180–182.
16 黄智超, 程建高, 李飞, 等. 同步辐射压弯镜重力补偿方法[J]. 强激光与粒子束, 2018, 30(8): 180066. DOI: 10.11884/HPLPB201830.180066.
HUANG Zhichao, CHENG Jiangao, LI Fei,. Gravity compensation for bent mirror of synchrotron radiation[J]. High Power Laser and Particle Beams, 2018, 30(8): 180066. DOI: 10.11884/HPLPB201830.180066.
17 Mao C W, Jiang H, He Y,. Compensation for gravitational sag of bent mirror[J]. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2017, 853: 20–26. DOI: 10.1016/j.nima. 2016.12.020.
18 卢启鹏, 高飒飒, 彭忠琦. 同步辐射水平偏转压弯镜面形误差分析与补偿[J]. 光学精密工程, 2011, 19(11): 2644–2650. DOI: 10.3788/OPE.20111911.2644.
LU Qipeng, GAO Sasa, PENG Zhongqi. Analysis and compensation of slope error for synchrotron radiation horizontal deflected mirror[J]. Optics and Precision Engineering, 2011, 19(11): 2644–2650. DOI: 10.3788/OPE.20111911.2644.
Elliptic mirror finite element analysis of double drive compensated bending
MA Tianyu1,2LU Qipeng1WANG Dazhuang1PENG Zhongqi1GONG Xuepeng1SONG Yuan1
1()2()
In order to meet the technical requirements of synchrotron radiation beamlines for related optical components, a double-drive four-point roller bending mechanism is designed.This study aims to implement an unequal moment elliptical cylinder bending of high-precision large-size optical mirror through finite element analysis (FEA) simulation. [Methods] First of all, a reflector with an external dimension of 1 200 mm×70 mm×50 mm was taken as the research object. Based on the object distance of 26.5 m, the image distance of 13 m and the grazing incidence angle of 2.8 mrad, the pressure applied to the bending moment was calculated according to the theoretical ellipse shape equation and the beam deformation bending moment equation. Then, the FEA software was employed to simulate and analyze the double-drive four-point bending mechanism. The focusing mirror was subjected to single-point compensation, double-point compensation, three-point compensation and four-point compensation in the presence of gravity compensation torque. Finally, the simulation compensation surface results obtained by FEA were compared with the theoretical calculation results.The simulated application of unequal torque at both ends reduces the surface shape error from 0.81 µrad under single-point compensation to 0.075 µrad under four-point compensation, reducing 95.96% of the original error to the greatest extent. It can effectively reduce the elliptical bending surface shape error with theoretical value of 0.013 µrad, and the decreasing trend is gradually gentle.This study indicates that the double drive compensated bending mechanism is feasible and effective to improve the bending accuracy of large-scale elliptical mirrors under multi-point compensation, and has important theoretical guiding role and significance for the bending technology of synchrotron radiation beamlines.
Bending mechanism, Elliptical cylinder, Finite element analysis, Surface error, Synchrotron radiation
Supported by National Natural Science Foundation of China (No.11079035, No.61974142), Rising Light Talent Program, Changchun Institute of OpticsFine Mechanics and Physics, Chinese Academy of Sciences (No.E01672Y6Q0), State Key Laboratory of Applied Optics Open Fund (No.SKLA02020001A09)
MA Tianyu, male, born in 1996, graduated from Changchun University of Science and Technology in 2019, master student, focusing on the key technology of synchrotron beamline
LU Qipeng, E-mail: luqp@ciomp.ac.cn
2022-03-19
2022-01-06,
TL99
10.11889/j.0253-3219.2022.hjs.45.060101
国家自然科学基金(No.11079035、No.61974142)、中国科学院长春光学精密机械与物理研究所旭光人才计划(No.E01672Y6Q0)、应用光学国家重点实验室开放基金(No.SKLA02020001A09)资助
马天宇,男,1996年出生,2019年毕业于长春理工大学,现为硕士研究生,研究领域为同步辐射光束线关键技术
卢启鹏,E-mail:luqp@ciomp.ac.cn
2022-01-06,
2022-03-19
