简谐振动的运动方程推导及应用①

于洪杰

(齐齐哈尔工程学院基础部,黑龙江 齐齐哈尔 161005)

0 引 言

机械振动现象在自然界、工程技术和日常生活中普遍存在,如机器开动时各部分的微小颤动、心脏的跳动等现象都具有明显的振动特性[1]。机械振动也为学生学习地震学、建筑力学等后续专业课程提供必要的基础知识。而简谐振动可以说是机械振动中最基本的振动,其他复杂的机械振动可以视为多个简谐振动的合成[2]。为了研究机械振动现象的基本机理,阐明机械振动的一般规律,需要应用简谐振动的运动方程,进一步分析和求解相关问题,将振动现象及机理应用到专业学习过程中,而在教育教学过程中,各类教材中对于简谐振动的运动方程推导较少,导致学生只知道方程的形式,不能很好的理解方程的推导过程。本文采用三种方法对简谐振动的运动方程进行推导,同时结合实际问题阐述简谐运动方程的简单应用,对各高校教师教育教学及大学生自主学习具有一定指导及借鉴作用。

1 简谐振动的运动方程推导

1.1 根据牛顿第二定律推导简谐振动的运动方程

以弹簧振子系统为例,根据胡克定律,物体所受的弹性力F 与物体相对平衡位置的位移成正比[3],比例系数k 为弹簧劲度系数F =-kx ,由牛顿第二定律F =ma ,可得ma=-kx

方程中x 表示简谐振动过程中物体离开平衡位置的位移,A 代表简谐振动物体离开平衡位置的最大距离,称为振幅,ωt+φ表征任意时刻物体振动状态,称为相位,φ为t=0时刻物体振动状态,称为初相。

1.2 根据机械能守恒定律推导简谐振动的运动方程

利用 “机械能守恒定律”对简谐振动方程进行推导时,可以将小球与弹簧作为研究的对象[4]。该模型中除了弹簧弹力外,其他的力都不做功,可以通过机械能守恒定律对简谐振动运动方程进行推导。

对于简谐振动,取平衡位置为坐标原点,如果从平衡位置开始计时,则振动位移方程为x =Asinωt;如果从振动端点开始计时,则振动位移方程为x=Acosωt[5]。实际应用过程中,可以根据实际需要来选择合适的位移方程进行解决问题。

1.3 根据简谐振动动力学方程的解推导简谐振动的运动方程

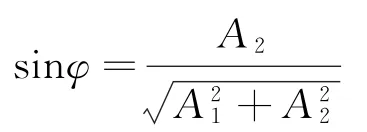
则x=A(cosφcosωt+sinφsinωt),即得简谐振动的运动方程x=Acos(ωt+φ)

从推导中可以分析出,简谐振动的位移是时间的余弦函数,简谐振动物体的速度和加速度也是按正弦或余弦函数随时间变化;在LC 振荡回路的中,电容器电量、储存的电场能等物理量也是按正弦函数随时间作周期性变化的[6]。

2 简谐振动运动方程的应用

2.1 已知简谐振动参量求受力问题

在实际工程中,经常会涉及到如图1 所示模型:轻弹簧上端与木板相连,木板上安装质量为m=1.0kg的物体,设木板沿竖直方向作简谐振动,其振动的周期T =0.5s,振动幅度A =3.0×10-2m 。求:当木板运动到最低点时,物体对木板的作用力大小。

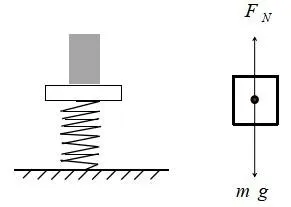
图1 简谐振动模型实际应用I

受力分析如图1所示,根据牛顿第二定律可得

由于物体是随板一起作简谐运动,根据前面推导的简谐振动的运动方程x=Acos(ωt+φ),对方程求二阶导数可得加速度

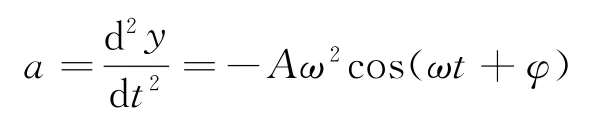
则FN =mg+mgω2cos(ωt+φ),重物在最低点时,相位ωt+φ=0

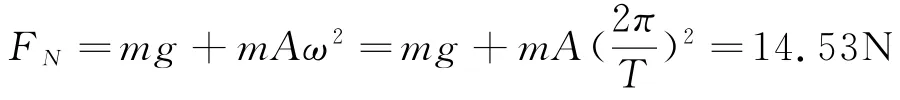
2.2 已知运动情况求简谐振动参量

轻质弹簧的劲度系数为k,上端与质量为m的平板相连。现有一质量为m的物体由平板上方h高自由下落,同时与平板发生非弹性碰撞。求振动的振幅、周期及初相。(以平板开始运动时刻为计时起点,向下为正方向)

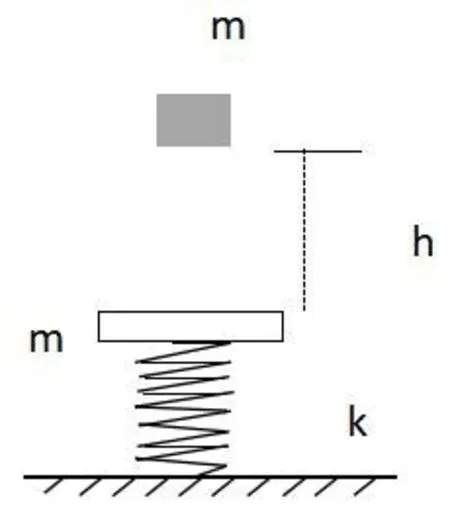
图2 简谐振动模型实际应用II

平板和物体做简谐振动,以平衡位置为坐标原点,向下为正方向,初始条件

3 实验结论

大学物理教材中一般采用动力学方程直接给出简谐振动的运动方程,学生知其然而不知其所以然。通过3种方法求解简谐振动的运动方程,不同方法在求解过程中循序渐进地培养学生逻辑思维能力。根据求解的简谐振动运动方程,结合实际工程问题模型,从已知简谐振动参量求受力问题和已知运动情况求简谐振动参量两个角度对简谐振动方程进行实际应用,提高学生解决实际问题的能力,对后续专业课程的学习起到很好的作用。