基于区间交叉效率DEA 和SMAA-2的毕达哥拉斯模糊偏好关系决策方法①

赵 珏, 刘金培, 刘迎凤

(安徽大学商学院,安徽 合肥 230601)

0 引 言

在决策过程中,决策者通常针对备选方案集给出方案两两比较后的偏好关系。但由于决策者所掌握的信息量有限,且决策环境不断变化,决策者往往不能用精确值来表示其偏好关系。基于此,Yager 等[1]在 直 觉 模 糊 集(Intuitionistic fuzzy sets,IFSs)等的基础上,首次提出了毕达哥拉斯模糊集(Pythagorean fuzzy sets,PFSs),这一方法不仅可以从隶属度、非隶属度、犹豫度三方面表示模糊信息,而且将隶属度与非隶属度的取值范围由三角形扩充为四分之一圆,是处理不确定性问题的一个强有力工具。杨艺等[2]在此基础上,提出了毕达哥拉斯模糊偏好关系(Pythagorean fuzzy preference relation,PFPR)的基础框架。近年来,关于毕达哥拉斯模糊信息的决策问题已经成为人们研究的热点[1-4]。学者们通常对偏好关系进行一致性调整后推导出其权重向量并进行排序,然而,一致性调整的方法容易歪曲决策者给定的原始评价信息,使得结果可信度较弱。此外,交叉效率DEA 作为衡量相对效率的工具之一,通过决策单元交互评价,可以使得最终评价结果更具客观性,且避免了对偏好关系进行一致性调整。但是,很少有研究将毕达哥拉斯模糊偏好关系与交叉效率DEA 进行结合。针对上述问题,提出了基于区间交叉效率DEA 和SMAA-2 的偏好关系决策方法,有效避免了决策信息的损失,具有较好的适用性与可行性。

1 预备知识

针对某一决策问题,设X={x1,x2,…,xn}为备选方案集,专家在进行决策的过程中,通常对备选方案进行两两比较,给出偏好关系矩阵R=(rij)n×n。

定义1[5,6]设X={x1,x2,…,xn}为备选方案集,若偏好关系R =(rij)n×n满足

其中rij表示备选方案xi优于xj的程度,则称R 为加性偏好关系。若该矩阵满足

则称偏好关系R 满足加性一致性。

为了表达决策者的不确定性偏好,区间模糊集、毕达哥拉斯模糊集的概念被提出。

定义2[2,7]论域X 上的区间模糊集(interval-valued fuzzy sets,IVFSs)定义如下:

其中lA(x)与uA(x)分别表示元素x 隶属于集合A 的隶属度区间的下限与上限,且满足0 ≤lA(x)≤uA(x)≤1。称[lA(x),uA(x)]为区间模糊数(interval-valued fuzzy number,IVFN),一般用α=[lα,uα]表示。

定义3[2,7]设IVFN 的中心值为center(α),不确定性程度为len gth([lα,uα])=uα-lα。对于任意两个IVFNα=[lα,uα]和β=[lβ,uβ],有如下IVFN 的比较规则:

(1)若center(α)＜center(β),则α ≺IVβ ;

(2)若center(α)=center(β),则

若len gth(α)＞len gth(β),则α ≺IVβ ;

若len gth(α)=len gth(β),则α=IVβ 。

2 决策方法

2.1 毕达哥拉斯模糊偏好关系的转换

首先利用模糊数之间的替代关系,将毕达哥拉斯模糊数转换为区间模糊数,同时毕达哥拉斯模糊偏好关系也可转换为对应的区间模糊偏好关系。

文献[2]提出,可通过等式ζ(p)=ζ(＜ρ,σ＞)=[ρ2,1-σ2],将p 转换成区间模糊数,同时也可将加性一致性PFPR 转换成加性一致性IVFPR,具体转换关系如下表1所示。

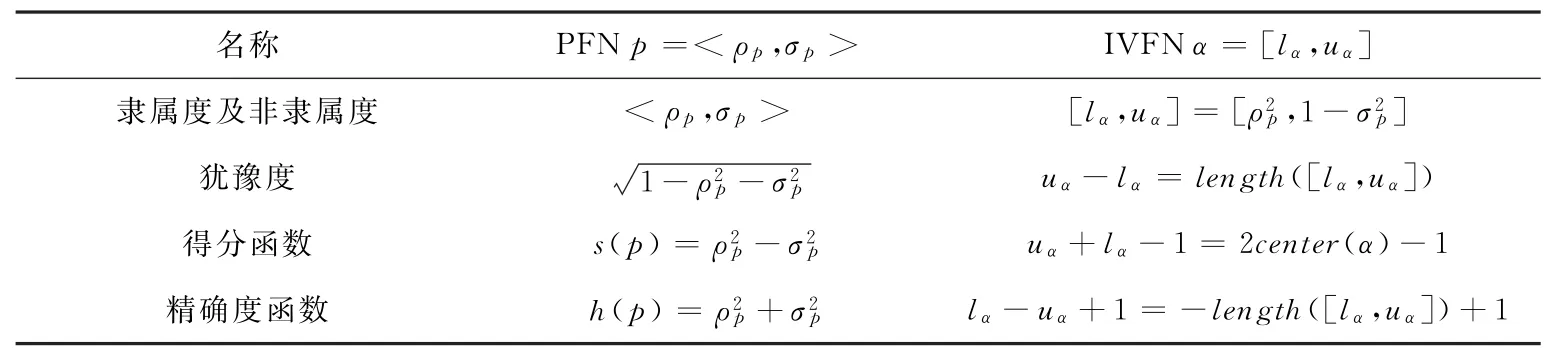
表1 PFN、IVFN 之间的替换

根据定义3、7,易得如下定理1。

定理1[2](保序性)设pi =＜ρi,σi＞(i=1,2)为两个毕达哥拉斯模糊数,若两个区间模糊数αi(i=1,2)满足αi =[ρ2i,1-σ2i](i=1,2),则p1≺Pp2⇔α1≺IVα2。

定理1表明,转换后的区间模糊数保持了原始毕达哥拉斯模糊数之间的序关系不变,说明模糊数之间的等价转换保证了信息的一致性。

2.2 毕达哥拉斯模糊偏好关系的区间交叉效率DEA 模型

在自评价效率的基础上,构建区间交叉效率DEA 模型,提出毕达哥拉斯模糊偏好关系的区间交叉效率的算法。

由表2,构建如下产出导向的CCR 模型(10),对决策单元DMUk(k=1,2,…,n)进行自评价效率计算[10],具体形式如下:

表2 基于=(ij)n×n =(＜ρij,σij ＞)n×n的投入产出表

表2 基于=(ij)n×n =(＜ρij,σij ＞)n×n的投入产出表

产出1 产出2… 产出n 虚拟投入

?

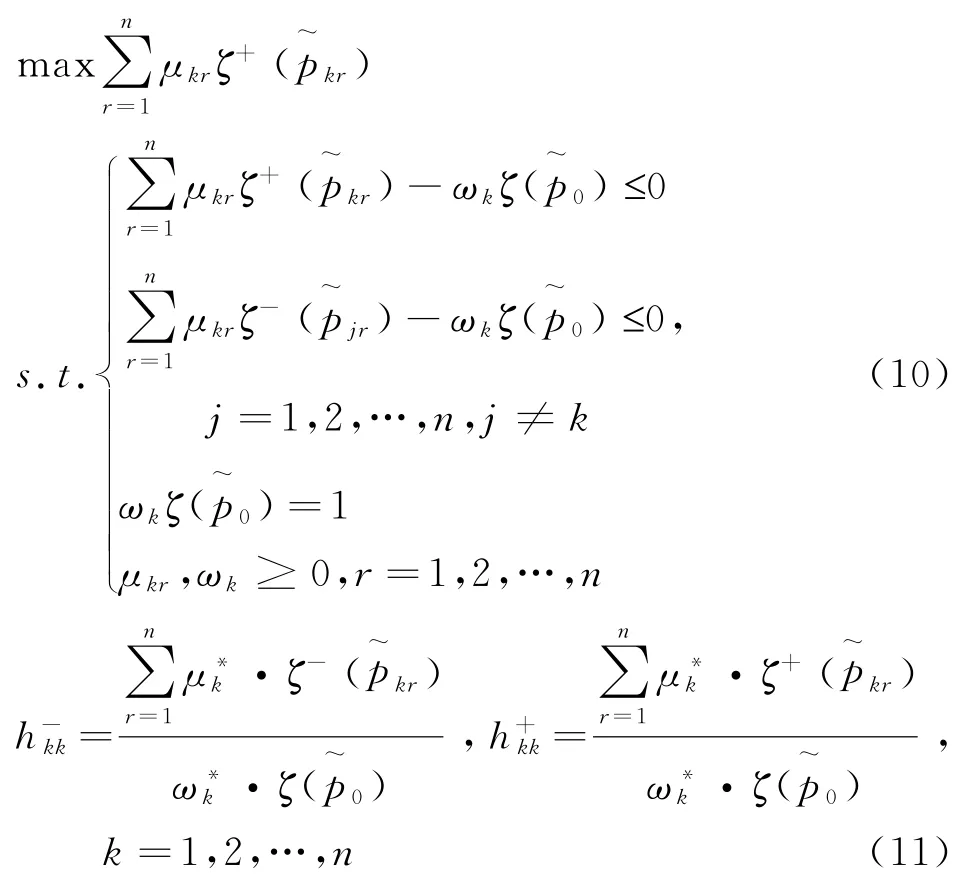
其中,ωk,μkr(r=1,2,…,n)分别表示虚拟投入变量与产出变量的权重值,对模型求解,得最优权重解(ωk*,μk*1,μk*2,…,μk*n),即使得DMUk效率最大时的权系数,以及DMUk的最优自评价效率区间[hk-k*,hk+k*]。

由于自评价效率模型存在决策单元过分夸大自身优势、回避自身缺陷等主观性偏差问题,因此引入交叉效率DEA 模型,通过将他评价效率与自评价效率相结合,提高结果的客观性。此外,决策单元的信息尚未确定,这将影响自评价与他评价效率的评估,因此传统的交叉效率模型并不适用于基于区间型数据的决策单元,基于此,建立以下模型,计算区间型交叉效率[11-13]。

首先,构建模型(12),求解得最优权重值(η*k,w*k1,w*k2,…,w*kn)以及目标函数值α*kk,即DMUk的相对效率值,其中,区间聚合函数在此基础上,构建进取型交叉效率DEA 模型(13)。该模型以保持DMUk的最优效率上限值为核心,目标在于最小化所有备选方案的全部交叉效率的下限值,求解得输入与输出变量的最优权重解uk*= (uk*1,uk*2,…,uk*n)T和vk*。因此,备选方案xk对xj的交叉效率评价值如公式(14)所示,θk-j与θk+j分别是他评价效率的区间下限与上限,即[θk-j*,θk+j*]表示方案xk对xj的评价值。

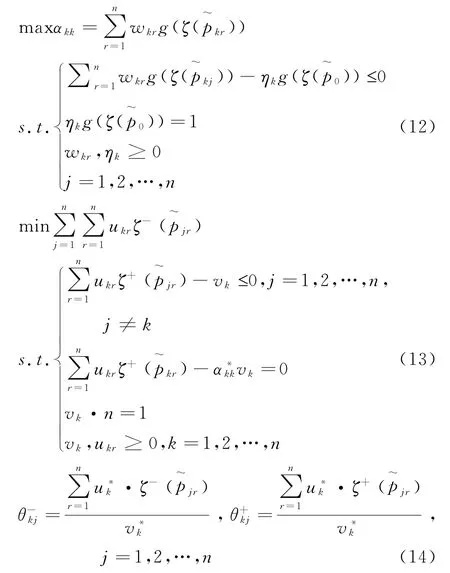
根据模型(10)、(12)以及(13),可获得区间交叉效率矩阵Θ ,即

2.3 基于SMAA-2的区间交叉效率排序

SMAA 方法能够在精确属性值、决策偏好未知或较少的情况下解决多属性决策问题,后改进的SMAA-2方法能够考虑每个方案随机排序的可接受度,这为决策者提供了一种基于多标准的指标评价方法。

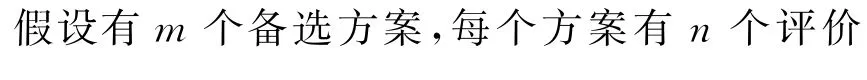
Step3 根据获得的区间交叉效率矩阵,利用模型(16)等计算出各个方案的排名可接受度指数bri(i,r=1,2,…,n)以及总体可接受度指数ahi(i=1,2,…,n),进而根据总体可接受度指数进行排序,最终得到备选方案集的决策结果。

3 算例分析

“十四五”时期是我国推进生态文明建设的关键时期,作为碳排放总量世界第一的大国,我国工业总体上仍未走出发展模式困境,环境保护仍面临能源约束、环境质量要求提高等多重压力。广东省深圳市作为全国首批 “无废城市”建设试点之一,需要进一步加快绿色发展转型,全面推动高质量发展。现有4个推动产业绿色转型发展的方案供选择:x1:培育和发展节能环保产业;x2:打造绿色产业链等,构建绿色制造体系;x3:健全完善相关政策,深化碳交易在各领域的协同减排作用;x4:发展战略性新兴产业和未来产业,打造经济增长新引擎。

为更好地响应国家政策号召,推动产业高质量发展,需要对这4个产业转型方案进行决策,专家根据自身的知识储备,给出4个备选方案的毕达哥拉斯模糊偏好关系矩阵如下:

根据表1,则毕达哥拉斯模糊偏好关系的等价 区间模糊偏好关系为:

根据模型(10)和公式(11),利用Matlab编程,计算得毕达哥拉斯模糊偏好关系的区间自评价效率值:

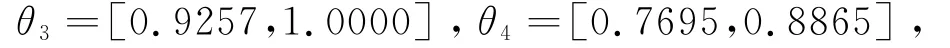
根据模型(12)和(13)的交叉效率DEA 算法,进一步计算得偏好关系的区间交叉效率值:

这里假设交叉效率值呈均匀分布,利用软件JSMAA 1.0.3版[15]中SMAA-2的方法,得出如表3所示计算结果。各方案按第二栏的总体可接受度指数进行排序,具体排序为DMU2≻DMU3≻DMU1≻DMU4,即方案1为最佳方案。

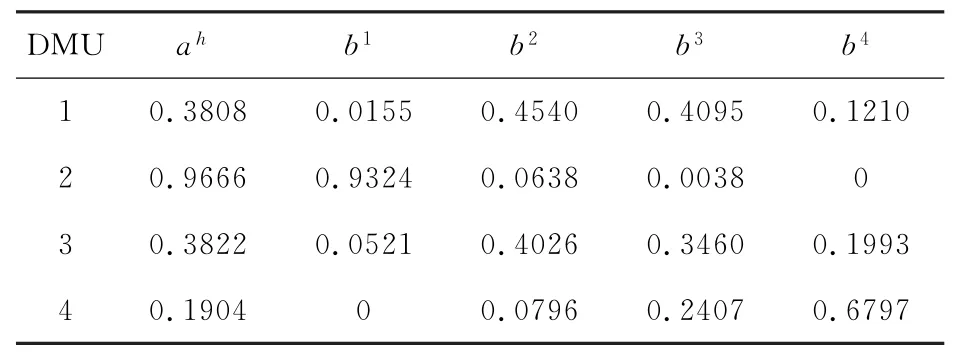
表3 总体可接受度指数及排名可接受度指数

4 结 语

针对毕达哥拉斯模糊偏好关系,本文将每个备选方案视为决策单元,提出一种新的基于区间交叉效率DEA 的决策方法。首先,将毕达哥拉斯模糊偏好关系转换为区间模糊偏好关系,构建方案自评价效率的求解模型。其次,构建偏好关系的交叉效率DEA 算法模型,得到自评价与他评价相结合的区间效率矩阵。最后,采用SMAA-2方法,获取所有备选方案的决策结果。本文提出的方法不需要对给定的偏好关系进行一致性调整,减少决策信息的损失,具有良好的适用性。