基于部分函数线性回归改进方法的CPI混频预测①

李气芳, 苏梽芳

(1.闽南师范大学数学与统计学院,福建 漳州 363000;2.华侨大学经济与金融学院,福建 泉州 362021)

0 引 言

在宏观经济和金融市场的混频数据分析中,传统的计量模型是利用加总或插值的方法转化成同频数据进行建模,这样会损失掉高频数据的大量信息。Ghysels等[1]提出混合数据抽样(MIDAS)模型,利用滞后权重函数把高频数据转化成低频数据,充分利用样本数据信息,大大提高模型的预测精度。Clements和Galvão[2]最先将MIDAS模型应用于宏观GDP 的预测。刘汉和刘金全[3]基于MIDAS 模型对中国宏观经济总量进行实时预报和短期预测。尚玉皇和郑挺国[4]提出一种包含宏观因子的混频短期利率模型对短期利率波动进行测度与预测。龚玉婷等[5]基于MIDAS-AR 模型、鲁王波和杨冬[6]基于半参数混频误差修正模型研究CPI的预测。

但是,MIDAS 模型在估计的时候,会面临权重函数类别和参数个数选择的问题。而金融领域的高频数据表现出函数型数据特征,可以利用函数型数据分析(FDA)理论来研究。该理论是由加拿大统计学家Ramsay首次提出[7],已经广泛应用到气象[8]、生物[9]、金融[10]、生态[11]等领域。于是,本文借鉴函数型数据分析思想,把高频数据看成是某个随机过程产生的函数曲线,利用部分函数线性回归模型对CPI进行混频预测,为混频数据分析提供一种新的分析方法。该模型由Zhang等[12]首次提出,程丽娟[13]把部分函数线性回归模型应用到上证指数的预测中,方连娣[14]在模型中加入辅助向量给出了极大经验似然估计。但现有部分函数线性回归模型估计和应用中,都假设函数型变量是服从独立同分布(i.i.d.)的,这显然与金融高频数据的相依特征不相符。于是针对相依的金融高频数据,本文提出部分函数线性回归模型估计的改进方法,并通过数值模拟和实例与现有的部分函数线性回归模型及MIDAS模型进行对比分析。

1 部分函数线性回归模型及改进模型的估计

1.1 模型介绍

Zhang等[12]提出了部分函数线性回归模型,包含1维标量因变量、p 维标量和1维函数型自变量,该模型把多元线性回归模型和函数线性回归模型结合在一起,具体的表达式为(1):

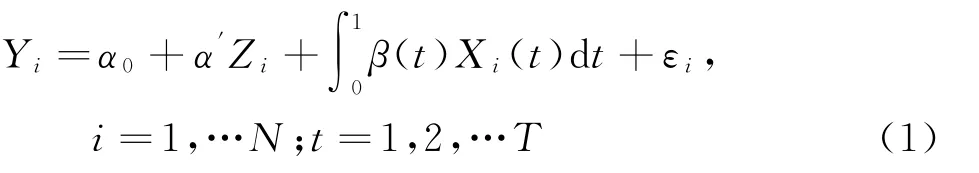
式(1)中Zi=(Zi1,Zi2,…,Zip)＇ 为p 维自变量向量,α = (α1,α2,…,αp)＇ 为p 维 回 归 系 数,Xi(t)为函数型变量且在[0,1]上平方可积,β(t)为回归系数函数,εi为随机误差项。

实际中,根据需要,很容易把模型(1)推广到两个或多个函数型自变量的情形,本文只考虑模型

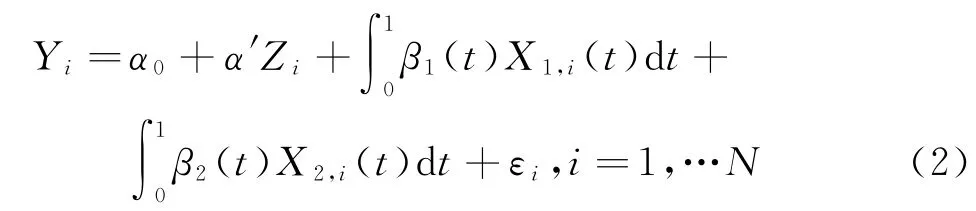
在模型估计之前,首要任务是把观测到的高频数据表示成函数曲线。

1.2 高频数据的函数表示

假设高频数据服从独立同分布(i.i.d.)假设,那么利用K-L展开式就可以表示为

由于金融系统的惯性,会导致金融高频数据之间具有相依特征,利用式(3)计算得到的样本协方差函数不再是总体协方差函数一致估计,所以式(4)的函数表示不够准确,也可能会导致模型估计出现偏差。于是把Wang等[15]的思想推广到函数型数据情形,提出一种基于残差协方差函数的函数表示方法:假设定义在时间[0,1]上的函数之间是相依的,比如金融市场今天和明天的某只高频股票价格曲线,那么在[0,1]的每个时间点t 上,N 条函数曲线的观测数据可以看成是一列相依的时间序列数据,利用AR(p)模型对每列相依时间序列数据进行拟合,从而得到i.i.d.的残差函数ηi(t),于是函数可以表示为

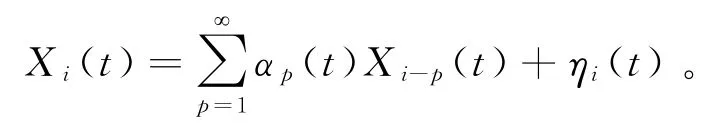
在得到i.i.d.的残差函数ηi(t)后,就可以利用i.i.d.条件下的FDA 方法计算残差协方差函数,再通过残差协方差函数计算得到残差函数主成分,进而利用K-L展开式把函数表示为

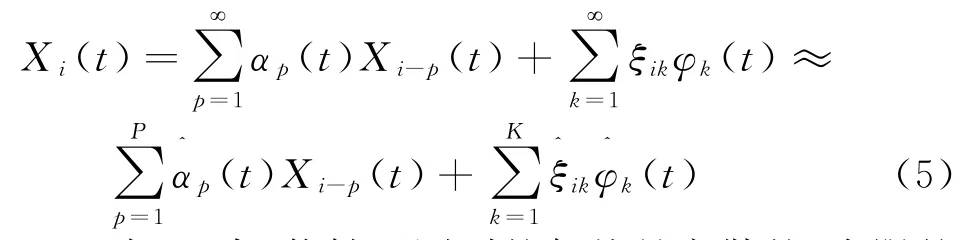
1.3 模型估计

对高频进行函数表示后,就可以代入模型进行估计,下面介绍两种估计方法:一种是现有的基于i.i.d.的协方差函数的估计方法,本文把它推广到二元情形;另一种是本文针对相依的金融高频数据提出的改进方法。

1.3.1 独立同分布(i.i.d.)条件下基于协方差函数的估计

假设函数型数据已经由式(4)表示成

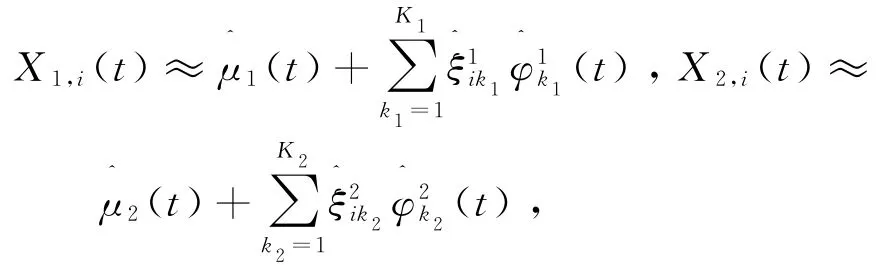
同时假设回归系数函数也可以用相同的函数主成分基线性表示,即有

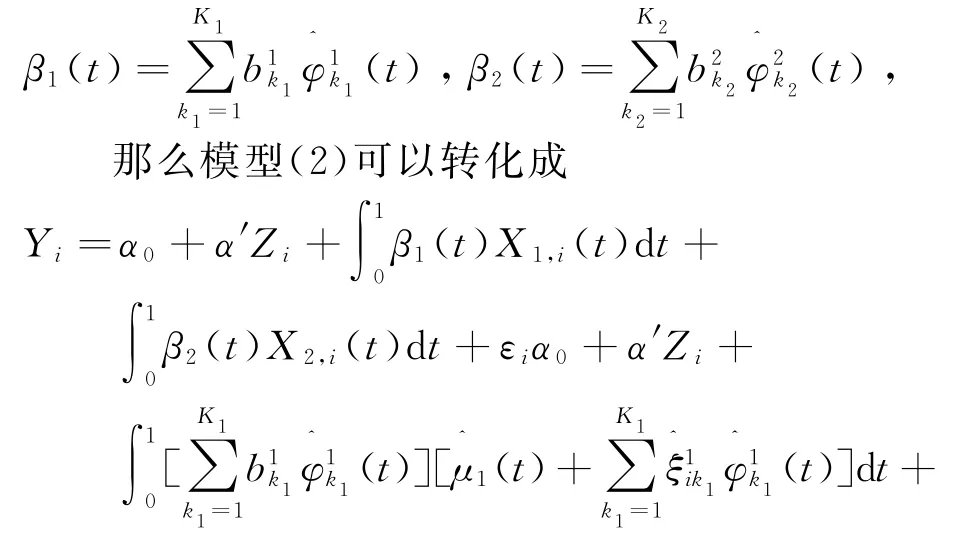
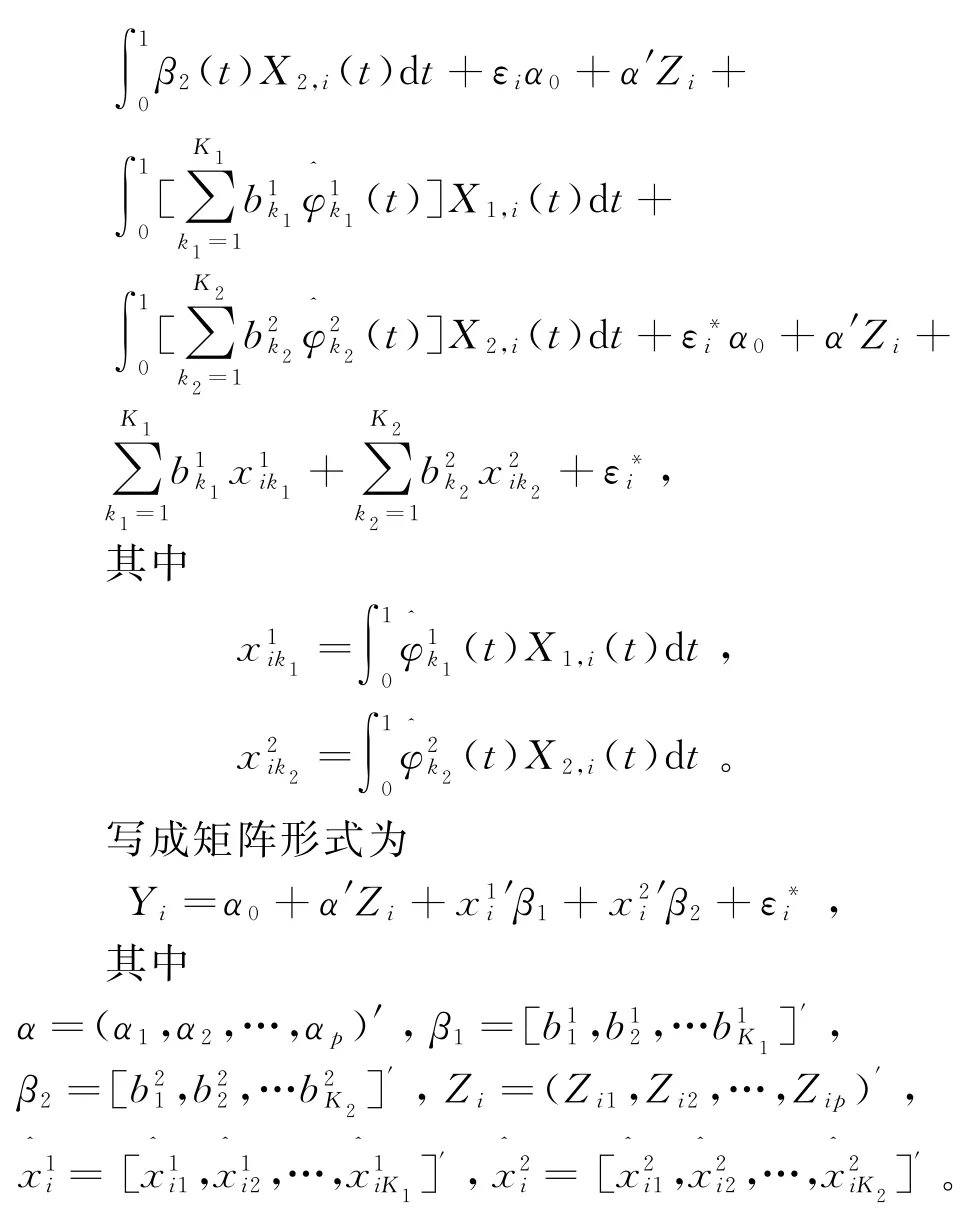
所以部分函数线性回归模型转化为多元回归模型,利用最小二乘法就可以估计得到回归系数向量

2 数值模拟

2.1 数据生成

参考已有研究,数据是由MIDAS模型

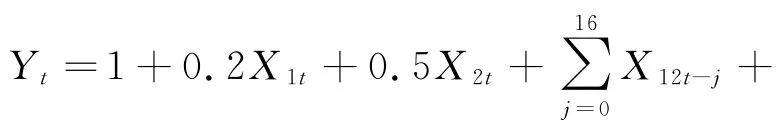
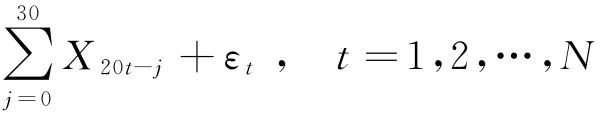
产生的,具体的模拟步骤如下:

(1)低频变量X1t和X2t由N(0,1)各生成(N+10)个数据,高频变量X3t由ARMA(2,2)生成12*(N+10)个数据,高频变量X4t由ARMA(2,2)生成20*(N+10)个数据。指数Almon 滞后权重多项式初始参数设定为γ1=（ 1 ,-0.5）＇,γ2=（ 2,0.5,-0.1）＇。 误 差 项εt由N(0,0.01)生成(N+10)个数据。这样生成的高频数据X3t和X4t具有相依特征。

(2)把生成数据代入MIDAS模型得到因变量Yt的值。前N个样本作为训练集,后10个样本作为样本外预测集。样本容量N分别50/100/200/300。

(3)利用M(2)-MIDAS和M(2)-MIDAS-AR(1)模型进行拟合,并得到样本外预测值1i和

2i。

(4)利用基于协方差函数估计方法估计回归系数函数,并进一步得到样本外预测值

3i。

(5)利用基于残差协方差函数的估计方法估计回归系数函数,并进一步得到样本外预测值

4i。

(6)计算均方预测误差平方根RMSPE。

(7)重复步骤1-6 共200 次,计算平均的RMSPE。

2.2 结果分析

数值模拟结果见表1,其中M(2)-MIDAS表示二元混频预测模型,M(2)-MIDAS-AR(1)表示滞后1期的二元混频预测模型,FPC 表示基于独立同分布(i.i.d.)条件下基于协方差函数的估计方法,RFPC表示相依条件下基于残差协方差函数的估计方法。

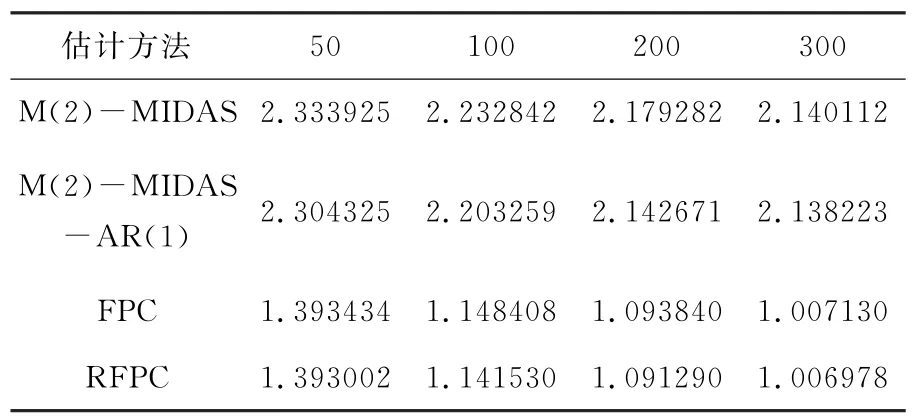
表1 不同估计方法的预测精度比较

从表1可以看出,随着样本量的增加,四种估计方法的样本外预测误差都呈现递减的趋势。在每个样本容量下,考虑了滞后1期的MIDAS-AR(1)模型比MIDAS的样本外预测误差要小;函数型数据分析方法FPC和RFPC的样本外预测误差比混频模型MIDAS和MIDAS-AR(1)的小;本文提出的基于残差协方差函数的估计方法RFPC的样本外预测误差最小。

3 CPI混频预测

影响CPI的因素很多,本文从货币供应量、生产水平、能源和农产品四个因素选择了月度同频变量M2和PPI、日度高频变量原油价格和豆类价格作为影响CPI的主要原因[5,16-17],同时考虑CPI滞后1期的影响。数据从2013年1月至2019年7月,其中2013年1月至2018年12月的月度数据和2013年1月1日至2018年12月31日的日度数据作为训练集,2019年1月至7月的月度数据和2019年1月1日至2019年7月31日的日度数据作为预测集。具体的部分函数线性回归模型为

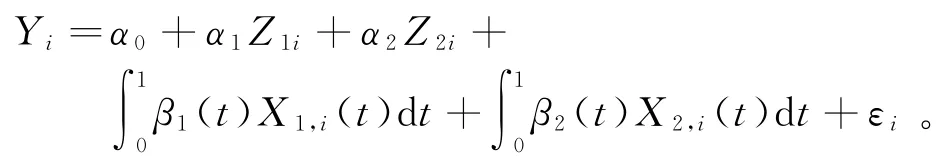
由于每个月天数28至31天不等且非交易日及节假日无数据更新,实际每个月观测18 至23天。参考已有研究,本文从每个月中选取20个交易日,对少量数据缺失部分进行插值。数据来自Choice金融终端,所有数据都以当月同比增长率来表示。基于R 语言,没有考虑CPI滞后期的预测结果见表2。

表2 不同估计方法的CPI预测精度比较

从表2可以看出,函数型数据分析方法FPC和RFPC的样本外预测误差比混频模型M(2)-MIDAS的小;本文提出的基于残差协方差函数的估计方法RFPC的样本外预测误差最小。下面加入CPI滞后1期,预测结果见表3。

表3 加入滞后1期后不同估计方法的CPI预测精度比较

从表3可以看出,加入CPI滞后1期后,三种估计方法的样本外预测误差都变小了。函数型数据分析方法FPC和RFPC的样本外预测误差还是比混频模型M(2)-MIDAS-AR(1)的小;本文提出的基于残差协方差函数的估计方法RFPC 的样本外预测误差最小。从表2和表3是可以看出,本文针对金融高频数据相依特征提出的改进方法在预测精度上具有一定的优势。

4 结 论

针对宏观经济和金融市场的混频数据,提出一种新的混频数据分析方法,把金融高频数据看成是由某个随机过程产生的函数曲线,利用部元函数线性回归模型对混频数据进行分析。并根据金融高频数据的相依特征,提出了模型估计的改进方法。结果表明:(1)数值模拟中,随着样本量的增加,四种估计方法的样本外预测误差都呈现递减的趋势,但在每个样本容量下,函数型数据分析方法FPC和RFPC 的样本外预测误差比混频模型MIDAS和MIDAS-AR(1)的小,且本文提出的估计方法RFPC的样本外预测误差最小;(2)CPI混频数据预测中,本文提出的改进方法比现有部分函数线性回归模型以及MIDAS模型的样本外预测误差要小、精度要高。