多楔带横向振动噪声仿真分析与试验研究

2022-06-27史尧臣宁凯唐武生尹春梅

机械科学与技术 2022年6期

史尧臣,宁凯,唐武生,尹春梅

(长春大学机械与车辆工程学院,长春 130022)

汽车多楔带是由带体橡胶、强力层线绳等组成的粘弹性复合材料体,一般用在汽车发动机前端传动系统中,通过带与带轮间的摩擦力将动力传递给空调压缩机、助力转向泵和发电机等附件[1-2]。由于汽车多楔带传动过程中,带与带轮之间的粘滞和滑动交替产生弹性滑动,导致张紧力幅值产生周期性变化,不可避免的产生振动和噪声[3-5]。尤其当弹性滑动产生的激励频率与带段的横向振动固有频率耦合时还会引起带体的共振和噪声[6-7]。这些异响会直接影响发动机的NVH性能。为了改善汽车多楔带传动过程中的噪声性能,Moon等通过试验发现当多楔带传动系统发生共振时多楔带振动幅值和噪声明显增大[8]。Michon等通过理论建模分析了带的横向振动幅值与外界激励频率、激励幅值之间的关系[9]。Parker等针对多轮传动系统建立了带的纵向运动梁模型,研究了张紧力和带轮转速对系统横向振动的影响[10]。epon等通过试验研究了带轮转速和张紧力对传动系统横向振动噪声的影响[11]。

目前,国内外针对多楔带传动噪声的研究主要集中在传动系统模型的建立和试验验证,在设计阶段对噪声进行预测分析的研究较少。因此,本文针对横向振动噪声,通过分析振动噪声产生机理,基于弦模型建立了多楔带振动方程,通过谐响应分析得到了多楔带振动响应,将振动响应作为边界条件预测了多楔带传动噪声的频响特性和声压分布规律,并通过两轮多楔带传动噪声试验验证了仿真分析结果。对汽车多楔带传动系统的减振降噪设计具有一定的意义。

1 多楔带横向振动噪声产生机理

汽车多楔带传动过程中的噪声主要包括带与带轮间相对滑动导致的摩擦噪声和由于振动导致的带体横向振动噪声。横向振动噪声是由于带与带轮间的粘滞滑动作用,使预紧力产生波动,导致带体在传动中产生横向振动,产生横向振动噪声。尤其当粘滑激励频率与带体固有频率耦合时,会产生较大的共振噪声。因此对多楔带横向振动噪声分析首先需要对多楔带的固有频率特性进行分析。由于多楔带的振动主要产生带跨度区域,因此建立单根带段跨度区域的振动模型如图1所示,设带与带轮楔入和楔出点间跨度长度为l,带速为v,带体的横向振动随位置和时间变化函数为w(x,t),张紧力为T。

图1 多楔带跨度区域振动分析模型图

由于多楔带截面尺寸相对跨度尺寸较小,所以一般采用弦模型建立微分方程[12-13]为

(1)

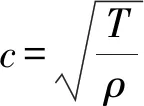
带传动过程中的带与带轮间的弹性滑动随转速变化一般可用正弦函数进行简化,设楔入处的激励频率wl(t)为

wl(t)=wlusinωt

(2)

设离楔入点距离x处的带体的稳态振动响应为

wl(x,t)=wu(x)sin(ωt+θ(x))

(3)

式中：wu(x)表示跨度区域内带体的最大振动幅值；θ(x)表示相位差。

将稳态响应代入微分方程中可得

式中：i表示虚数；W(x)为w(x,t)的复振幅。

W(x)=wu(x)eθ(x)i

(5)

将楔出和楔出处的边界条件代入式(5)得

W(0)=0 ,W(l)=wlue0i

(6)

将式(6)代入式(4)可得特征值为

(7)

设方程(4)的通解为

W(x)=Aeλ1x+Beλ2x

(8)

将特征值λ1和λ2代入式(8)得到方程通解为

(9)

依据边界条件求出特解为

(10)

已知

(11)

则特解可改写为

(12)

设跨度区域带段的一阶固有频率ω0为

(13)

则式(13)可写为

(14)

则跨度区域内带段的横向振动响应可表示为

(15)

当弹性滑动引起的激励频率与ω0的成整数倍时会因为耦合引起带段共振,产生较大的振动噪声异响[14-15]。由于带的传动速度相对波速较小,因此一般忽略带速的影响,则带段的各阶横向振动固频可简化为

(16)

2 两轮传动系统振动噪声仿真分析

为了预测由于横向振动导致的振动噪声,所以需要建立由谐响应分析和声学边界元分析组成的多楔带传动系统振动噪声分析流程。本文针对6PK汽车多楔带两轮传动系统进行仿真分析,多楔带结构参数及材料设置如表1所示。

表1 多楔带结构参数及材料设置表

将建立的两轮传动系统模型导入Workbench进行Sweep网格划分,网格划分后的传动系统如图2所示。

由于横向振动方向是导致带振动噪声的主要原因,为提高计算速度限制其它方向的自由度,通过计算求出带体的前6阶固频如表2所示。

表2 带体各阶固频仿真结果

模态分析只能得到带体的固有频率,为了进行声场仿真需要先求出带体在不同频率激励下的响应,并作为噪声仿真的边界条件进行求解。因此在带与带轮接触处施加激励,通过Workbench谐响应分析求得0～300 Hz范围内的传动系统的频响曲线，如图3所示。

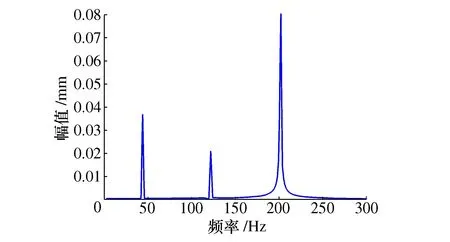
图3 两轮传动系统频响曲线图

可以看出当激励频率与带段横向振动固有频率44 Hz及其它阶频率耦合时会产生明显的响应峰值,这是由于激励频率与固有耦合而导致的共振现象。

将谐响应分析得到的带段振动数据作为边界约束进行声场仿真分析。在LMS中设置声场边界条件如表3所示。

表3 两轮传动系统振动噪声分析声场参数表

声场尺寸180 mm×150 mm×700 mm,由于带中点位置处振动最大,所以选取带跨度中点位置上的场点1和场点2进行分析,声场建立后的汽车多楔带两轮传动噪声仿真分析模型如图4所示。

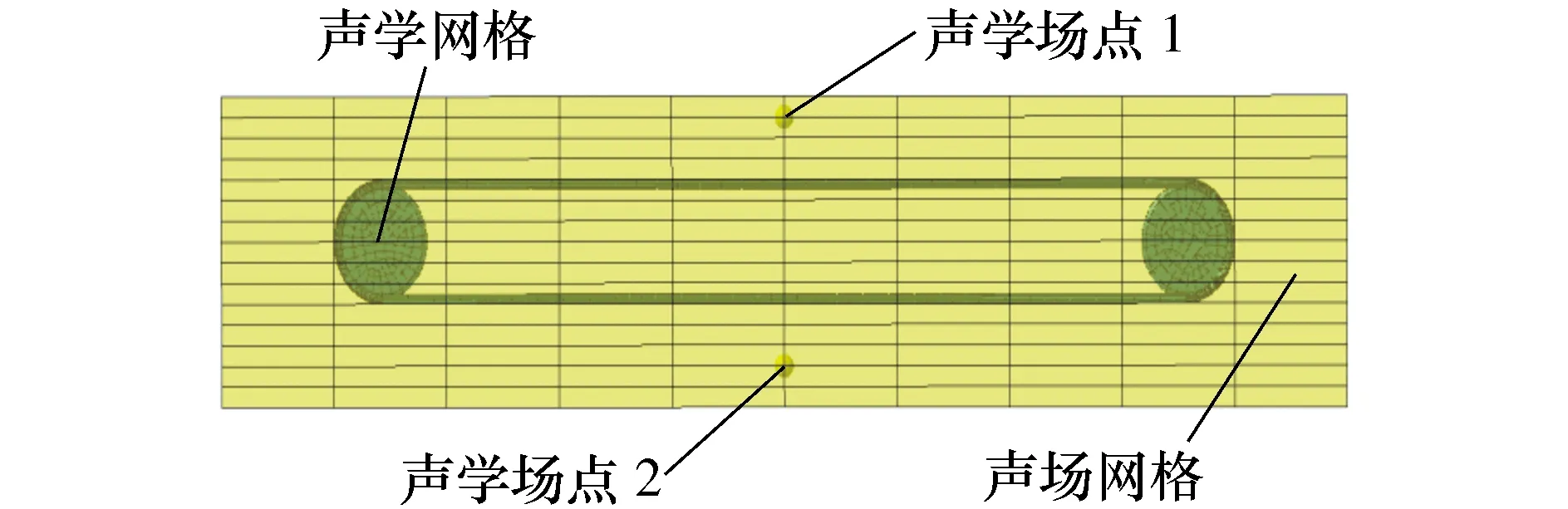
图4 多楔带两轮传动噪声仿真模型图

通过声场仿真得到场点1和2处的频响曲线如图5所示。

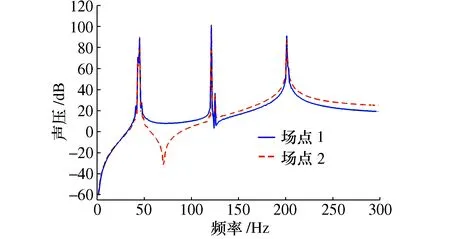
图5 场点位置处的声压频响曲线图

可以看出两个场点的噪声随激励频率变化规律基本一致,随着频率增加,噪声响应有一定的小幅度增大。当激励频率为固有频率44 Hz及其它阶固有频率时,有明显的噪声响应峰值,这是由于共振导致的明显共振噪声。

当激励频率为44 Hz时通过仿真得到多楔带两轮传动系统噪声声压分布如图6所示,可以看出噪声声源主要集中在声场中间位置,最大声压为90 dB,即上下带段跨度中点处噪声最大,这是由于中点位置处的振动幅值最大,与汽车多楔带振动噪声产生的机理分析一致。

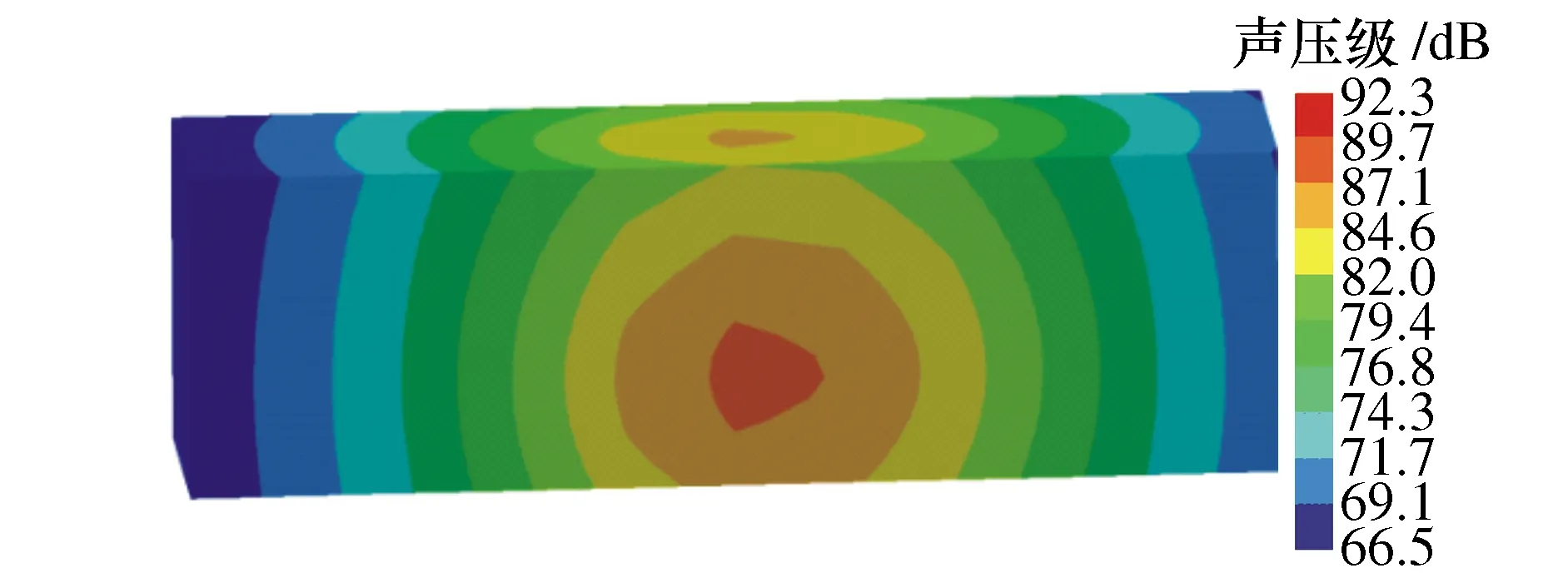
图6 44 Hz时两轮传动系统声压分布云图

3 噪声试验装置与结果分析

3.1 传动噪声试验装置

为了通过试验验证仿真分析结果,在汽车多楔带两轮传动噪声试验台上进行了6PK多楔带传动噪声试验研究。试验装置由声阵列传感器、两轮传动系统、隔音箱和振动测试系统等组成,如图7所示。多楔带带长1 260 mm,带轮节径60 mm。声压传感器采用8个INV9206声压传感器组成2行4列的阵列测试系统,行间距150 mm,列间距250 mm,声压传感器的采样频率20 kHz。振动测试采用宝利泰多普勒VXH-F-110激光测振仪,采样频率为50 kHz。

图7 汽车多楔带传动噪声试验系统图

3.2 噪声试验结果分析

通过试验得到张紧力为400 N,主动轮转速为900 r/min时的振动和噪声频域特性曲线如图8所示,声压分布云图如图9所示。

图8 多楔带振动和噪声频域特性图

图9 共振时多楔带声压分布云图

从图8中可以看出振动和噪声的频域信号均在带段固频44 Hz及其倍频处出现了较大峰值。由图9可以看出噪声声压主要集中在带段中间位置,此时最大噪声为85.3 dB,这是由于带段中间位置共振而产生的较大噪声集中,同时在带轮与带接触位置也有一定的声源分布,这是由于在楔入和楔出处的弹性滑动产生的摩擦噪声,由于相对滑动速度和滑移量较小,所占的声源比重较小。

随转速逐渐增加,激励频率逐渐增大,脱离带体横向振动的固频区域,当转速达到1 500 r/min时,通过噪声阵列测试系统得到的声压分布如图10所示,可以看出噪声已不再集中于带段中间位置,大部分噪声产生于楔入和楔出位置,以带与带轮的摩擦噪声为主,此时噪声声压也降为64.7 dB,属于正常传动时由于弹性滑动导致的摩擦噪声。