湿式离合器换段过程液压系统故障机理分析与诊断方法研究

王正幸,鲁植雄,陈元

(南京农业大学 工学院,南京 210031)

液压机械无级变速器(Hydraulic mechanical continuously variable transmission,HMCVT)是一种液压功率流与机械功率流并联的新型传动装置,通过机械传动实现传动高效率,通过液压传动的可控调速与机械传动相结合实现无级变速[1]。在实际设计过程中,机械结构基本保证了全寿命周期,但液压机械无级变速器的故障点一般出现在湿式离合器液压系统方面,因此湿式离合器液压系统的故障诊断成为不可避免的研究课题。为了使HMCVT湿式离合器液压系统具有平稳的工作特性,需要监测HMCVT工作过程中出现的故障,近年来对这一方面的研究日益增多。朱镇等利用BP神经网络、频段分步法、核方法分别识别电液比例阀、变量泵、湿式离合器液压系统故障,对液压系统的故障状态作了大致概括,构建了合理的诊断结构,实证了不同的诊断算法对于变速器的故障诊断能够给出正确结果[2]。王光明等利用湿式离合器液压系统的模拟故障,提取故障数据,并采用基于粗糙集理论与特征向量法对样本进行约减,采用基于Fisher准则与核方法对样本进行学习,对故障算法的鲁棒性进行测试,结果表明算法的平均识别率较高[3]。马冰青等通过遗传算法优化的BP人工神经网络对HMCVT湿式离合器液压系统故障进行诊断,试验结果表明遗传神经网络比传统神经网络准确率更高,故障诊断率达到94%,证明了遗传BP神经网络能够很好的解决液压系统的故障诊断问题[4]。张晓辉等利用BP神经网络对HMCVT液压系统进行故障诊断,试验结果表明BP多值分类法,对液压系统的故障诊断更加精准,从而证实油压与故障之间存在的相关联性[5]。Huang等提出了一种改进的PSO-BP液压系统故障诊断方法。首先对标准粒子群算法的惯性权值和学习因子进行改进,然后采用改进的粒子群算法对BP神经网络的权值和阈值进行优化,使得BP网络性能得到改善,该方法提高了BP网络的收敛速度,降低了诊断误差[6]。

为了解决湿式离合器在一定负载情况下,由于液压系统故障而出现离合器换段品质不良的问题,本文结合湿式离合器的工作特性提出了基于QPSO的BP人工神经网络模型,用来判定HMCVT湿式离合器换段品质不佳的故障原因。相较于传统PSO优化BP网络以及传统BP神经网络预测,能够极大的避免模型训练时进入局部极小和收敛速度慢的问题,从而更加精确的预测故障。

1 湿式离合器换段过程故障分析

1.1 液压系统压力、流量脉动故障机理分析

湿式离合器的换段过程大致分为4个阶段:第一阶段,油液迅速充满离合器活塞腔,压力刚刚克服回位弹簧初始压紧力,开始推动活塞移动;第二阶段,随着油压上升,作用在活塞上的油压推动活塞和摩擦副运动,消除钢片和摩擦片的间隙,主从动端开始产生转速差;第三阶段,摩擦副表面产生接触摩滑,随着油压的升高,摩擦表面的摩擦转矩逐渐上升,离合器主被动端的转速差逐渐减小,直至主被动端实现同步;第四阶段,当主被动端转速同步后,为保证离合器有足够的摩擦转矩储备,避免由于外力矩突然增加造成摩擦副打滑,因此该阶段使油压继续上升,最终达到系统油压设计值。在摩擦副接合阶段,控制油压上升的快慢以及幅值的大小对摩擦副主被动端接合时间影响很大,进而影响该阶段滑摩转矩。在湿式离合器换段期间内,接合充油压强不断提高,从动轴转速上升(摩擦副转速差下降)加快,缩短最终接合过程结束条件的时间;同时,接合过程的总接合转矩响应时间变快,且接合总转矩峰值也逐渐增大[7],因此在给定负载条件下,系统换段过程中充油压强的不稳定将会直接导致湿式离合器在接合过程中主从动轴长时间产生较大的转速差而一直处于滑摩状态,使湿式离合器换段品质不理想。本文将针对湿式离合器的该典型故障对液压系统进行研究。

湿式离合器工作压力、流量脉动将会影响湿式离合器接合特性,通过分析,引起该方面的主要因素:1) 液压系统管路故障带来的系统工作油压无法达到预设油压,使得湿式离合器在换段过程中无法正常接合;2) 液压系统电磁阀体的损坏、卡滞带来的故障,该故障也会引起液压路流量和压力受到扰动或者迟滞[8-9]。因此将引起湿式离合器换段不理想的液压系统故障源(包括正常状态)总结为以下5种:

1) Y0正常状态:表示液压系统处于正常工作状态,液压系统的压力、流量,等参数都正常,在这个模式下,所有的参数都是在正常指标的状态下测得。

2) Y1换段电磁阀阀芯卡滞:阀体采用电液比例换向阀,能够根据不同的输入电磁铁电流给出不同的稳态输出压力。而当杂质物质渗入时,电磁阀阀芯所受阻力增大,阀芯达到稳定正常状态所花时间比健康状态下长,或无法达到正常工作时的位置[10]。在额定流量情况下,阀芯位置的距离将直接影响换向阀的工作压差,压差的扰动将影响进入湿式离合器油腔内的油压,引起接合阶段供油压力不足,在实际台架试验的过程中多次发生电磁阀因油液杂质影响而导致换段不成功的情况，即

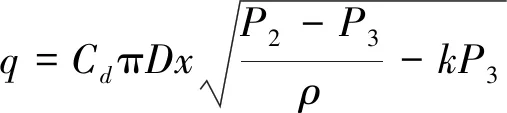
(1)

式中:Cd为阀口流量系数;D为换向阀活塞直径;x为换向阀阀芯位移;P2表示换段电磁阀进压;P3表示换段电磁发出口压力;ρ表示油液密度;k表示换向阀泄露系数。

3) Y2溢流阀阻尼孔堵塞故障:溢流阀本身组件比较多,为了保持系统的压力,湿式离合器液压系统工作频率较高,随着工作时间的延长和开关状态的不断切换,溢流阀很可能发生主阀阻尼孔的堵塞以及无法及时回位等退化问题[11]。由流经溢流阀阀口处的流量可得：

(2)

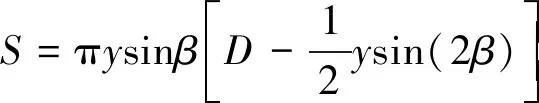
(3)

式中:α为阀口处流量系数;PL为入口压力;S表示通流面积;y表示阀芯位移;D为阀孔处孔径。当阀口阻尼孔发生堵塞时,将会导致阀孔处孔径减小,直接影响通流面积的大小,导致阀口流量的不稳定。

4) Y3液压系统泄露:液压管路由于零部件安装问题,或者在实际运行过程中振动引起的旋转接头松动导致的油液泄露故障,使得离合器动作迟缓,油压难以正常建立,该种情况难以判断。正常情况下的漏油,泄漏量很小,不会对工程装备的正常工作造成影响,本文研究的是不正常泄漏,需要进行有效预测。

5) Y4过滤器堵塞故障:湿式离合器液压系统的油液质量是保证整个系统平稳运行的前提,而过滤器过滤性能的保持,将直接决定系统的油压、流量是否满足要求。在一定的流量下,过滤器前后产生压差,这个压力差为过滤器的阻力,也是压力损失值,在其无损的情况下,其数值理论上应尽可能小[12]，即

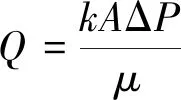
(4)

式中:k为过滤器通油能力系数;A为液体流经有效通流面积;ΔP表示进出口压差;μ表示油液动力粘度。过滤器在实际工作过程中吸力较大,将非常容易发生过滤器堵塞,在额定流量的情况下,将会导致通流截面积减小,间接引起油路压差增大,最终导致流入离合器油缸内液压油压力不足,在换段时间内使得接合不完全,离合器换段不成功。

1.2 液压系统故障数据特征提取

仿真试验以南京农业大学自行研制的HMCVT湿式离合器液压系统为研究对象。考虑到各段离合器油路构成一致,下面以其中C1离合器为例,参数见表1。

表1 C1离合器内部参数表

湿式离合器油压相关公式为

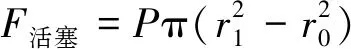
(5)

(6)

根据式(5)和式(6),初步计算湿式离合器在负载1 000 Nm情况下的正常工作最大油压为4.02 MPa,设定液压系统工作的流量为8.5 L/min,发动机转速为1 000 r/min,利用AMESim建立湿式离合器液压系统的仿真模型,将不同类型的故障模拟注入如图1所示的湿式离合器液压系统模型中[13]，为验证QPSO-BP算法提供数据来源[14-15]。

图1 湿式离合器液压系统模型图

Y1类型故障:在AMESim系统中为了模拟这一过程,可以通过改变电磁阀阀芯位移x来模拟阀芯卡滞程度。因此,模拟电磁阀卡滞则只要设置x即对应于相应的卡滞程度。

Y2类型故障:保持溢流阀的其他参数不变,设定在正常状况下的主阀阻尼孔的直径和堵塞故障状况下的主阀阻尼孔的直径D。

Y3类型故障:通过在液压管路上放置节流阀,并给定不同的输入信号k,模拟其等效的管路泄露。

Y4类型故障:通过改变过滤器管路内管路直径d,改变通流面积模拟不同程度的管路堵塞情况。

4种故障注入参数如表2所示。

表2 故障注入参数表

图2分别是注入4种故障状态后,湿式离合器在换段过程中主从动轴实际转速差。图2中可以看出湿式离合器主从动轴速度差在整个换段时间内长时间过大,产生了不同程度的滑摩,甚至打滑,换段过程不理想[16]。

图2 不同故障状态下的转速差

常见的引起湿式离合器换段不理想的故障类型主要有换段电磁阀阀芯卡滞、溢流阀阻尼孔堵塞故障、液压系统泄露、过滤器堵塞故障这4种故障模式及正常状态,将5种状态设为故障集S={y1,y2,y3,y4,y5}。湿式离合器液压系统的故障征兆则主要从油液流量L,压力P指标考虑。但是在实际数据提取的过程中,由于油压曲线较为平稳,因此只提取均方根值作为特征参数;而流量曲线波动较为明显,故利用其时域特征作为故障特征提取的参数如表3所示。

表3 时域特征参数

2 故障诊断算法及测试分析

2.1 QPSO优化BP神经网络故障诊断模型

鉴于传统的PSO算法容易陷入局部收敛,且极大依赖速度更新的范围。新引入的QPSO算法结合量子进化理论来提升全局的搜索能力。

粒子在空间中的位置和速度不能够一起确定,粒子的位置用波函数表示,求解的方法主要使用蒙特卡罗方法,本文使用MATLAB实现量子粒子群优化算法。QPSO优化算法的粒子更新位置公式为:

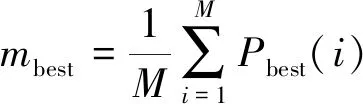
(7)

P=β·PISbest(i)+(1-β)·Gbest

(8)

式中:mbest为粒子群体所在最佳平均值；Gbest表示粒子群体所在最佳值；PISbest(i)表示粒子个体最佳值；β是随机数,β∈[0,1]。当β∈[0，1]时,粒子群在全局搜索过程中的收缩与扩张更新表达式为

(9)

式中:gen表示进化次数;maxgen表示最大进化次数。QPSO进化方程为

(10)

式中:u与b的取值范围相同;X、x分别为进化前后的最优位置。量子粒子群优化算法(QPSO)容易实现,在模型的实现过程中,所需要调节的参数少,在全局的最优解搜索能力强,不易出现局部最优[17-18]。

2.2 QPSO-BP的算法分析

故障征兆集是液压系统采集的信号经过特征提取以后的值,在BP神经网络中输入层的个数为6个。由于故障集元素有5个,所以网络中的输出层的神经元个数为5个。根据经验公式,隐藏层神经元个数为6个,隐藏层的激活函数使用Sigmoid函数。基于湿式离合器液压系统的QPSO优化BP神经网络实现流程如下:

1) 根据故障的产生原因,通过AMEsim获取不同故障情况下的故障数据,并进行特征提取,得到100组特征数据,每组6个输入,并进行归一化处理,处理后作为神经网络输入。

2) 创建BP神经网络,随机初始化权值、阈值,对神经网络权值和阈值进行编码,确定寻优维度为77。

3) 设定种群规模为10,确定粒子个数,随机初始化粒子速度与位置,速度与位置的产生范围在[0,1]之间,最后做迭代计算,确定最大寻优迭代次数为100。

4) 计算粒子适应度,选用测试样本的误差均方差作为适应度函数,且记录全局极值,设计适应度函数为

(11)

式中i表示特征值的数量。

5) 设定目标误差为0.01,通过对不同代数的权值和阈值进行更新,保证适应度函数值接近目标值。

6) 更新每个粒子的速度与位置。

7) 增加迭代进化数,判断是否收敛,记录全局极值。当系统每一次优化后的输出满足:

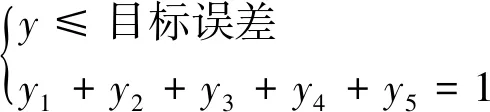
(12)

y=max{y1,y2,y3,y4,y5}

(13)

结果取本测试结果的最大值,即每一次计算的误差小于目标误差,且不同模式的故障发生概率总和为1,将此次的结果作为神经网络输出。通过标签转换为,将最终输出粒子位置设置为BP神经网络各个连接层的权值和阈值,从而优化BP神经网络。

利用QPSO算法求BP算法最优的初始化参数,为每个种群计算适应度值,并保存在f-pbest中,将最优适应度的种群参数保存在gbest中,记录最优适应度f-gbest循环迭代100次,寻找最优参数。初始化时生成随机向量β、u,计算种群参数的平均值mbest为每个种群i的参数利用公式更新。

分类结果如图3所示,其中横坐标为50组测试数据,纵坐标显示实际的输出与期望输出是否吻合。

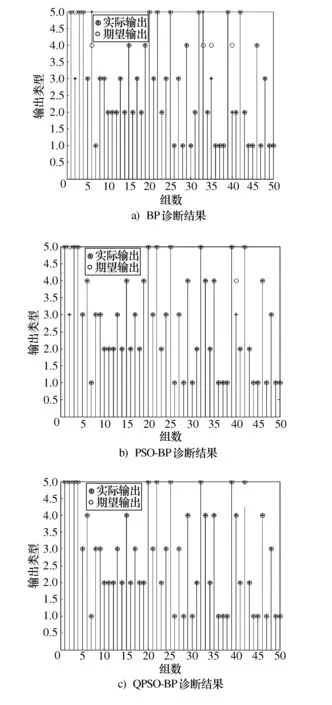
图3 故障诊断结果

QPSO-BP算法使用100组数据样本,每组样本有90个数据,通过特征提取得来。特征提取后的输入个数为6,输出类型数为5。将100组数据的50%作为训练样本,剩下的作为测试样本,由图3对比可以看出,采用BP神经网络算法的准确率为90%,传统PSO-BP的诊断效率为96%,而QPSO优化后的准确率达到了98%。通过如图4所示的算法收敛曲线可以看出QPSO算法经过15次迭代后收敛,收敛速度明显优于传统PSO算法,PSO收敛精度在0.015左右,而QPSO的收敛精度基本达到设定误差0.01,收敛精度明显更优。

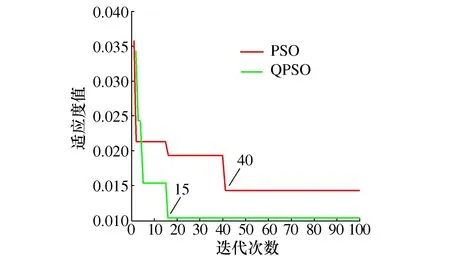
图4 算法收敛曲线

3 台架试验

如图5所示,搭建湿式离合器液压系统故障诊断试验平台,通过实际模拟4种故障,提取故障特征参数,进一步验证QPSO优化BP诊断算法的精确性。将发动机维持在额定转速1 000 r/min 附近,电涡流测功机给定负载1 000 Nm。实际台架主要设备具体选型如表4所示。

图5 湿式离合器液压系统台架

表4 试验设备

3.1 台架故障模拟试验

Y1换段电磁阀阀芯卡滞故障设计:考虑故障模拟在实际操作中的可行性,本试验设计电磁阀阀芯卡死故障进行模拟。通过在阀芯与腔体内侧塞卡滞物进行模拟(具体试验操作时,是在通油口塞入硬纸片,阻碍阀芯运动)。

Y2溢流阀阻尼孔堵塞故障设计:阻尼孔被堵塞,是比较常见且容易被忽视的问题,这是由液压油不纯,油中杂质太多引起的。试验采用使用可调阻尼孔的溢流阀,模拟故障状态。

Y3管路泄露故障设计:通过在油缸的油管接口处旁路外接节流阀,并调节节流阀的开口大小,人为的复现了不同程度泄漏的故障状态。

Y4过滤器油路堵塞故障设计:过滤器的滤网堵塞会增加滤网的阻力,其阻力值不会一直增大,而是随着系统循环泵的起停往复地变化。当滤网的滤芯严重堵塞无法恢复时,滤器的阻力会显著增加,严重影响支路流量的稳定性,本试验采用油液铁屑设计实际的堵塞故障状态。

故障模拟试验实际故障点如图6所示。

图6 实际故障点

3.2 测试结果

根据故障模拟,通过labview采集每种类型10组数据,采样频率200 Hz,共50组不同故障情况下的压力、流量数据。对于该故障诊断系统,不仅要求其能够在稳态时发现故障,也要求其具备在非稳态时发现故障的能力,因此在训练集和测试集中包含渐变故障,试验样本覆盖不同程度的故障情况。

在离合器控制油路中加装压力传感器(NS-F,0～10 MPa)与流量传感器(LWGB-4,0～0.4 m3/h)分别用于测量C1段离合器充油压力与主油路充油流量。图7和表5为在台架模拟的不同故障状态下,液压系统所采集到的实际流量与压力数据的部分图表。可以看出,在换段的第二阶段压力数据存在重叠,在未换段成功时压力数据增长的趋势基本相似;流量数据在换段阶段也无法通过简单的阈值判断实现数据样本的正确分类,样本的取值范围均与其他故障模式下存在区域重叠。因此结合QPSO-BP仿真试验算法,通过训练不同程度的故障数据来优化权值、阈值矩阵,作为试验的初始化参数,对试验模拟的故障进行预测。

图7 部分流量、压力原始数据

表5 试验结果对照表

通过表5可以看出:传统PSO优化BP相较于BP算法进一步提高准确率,但根据式(12)和式(13),QPSO的预测类型数值区分度明显,更加接近期望输出。图8最终优化后的QPSO算法准确率达到98%,算法平均时间基本可以满足实际工程应用。

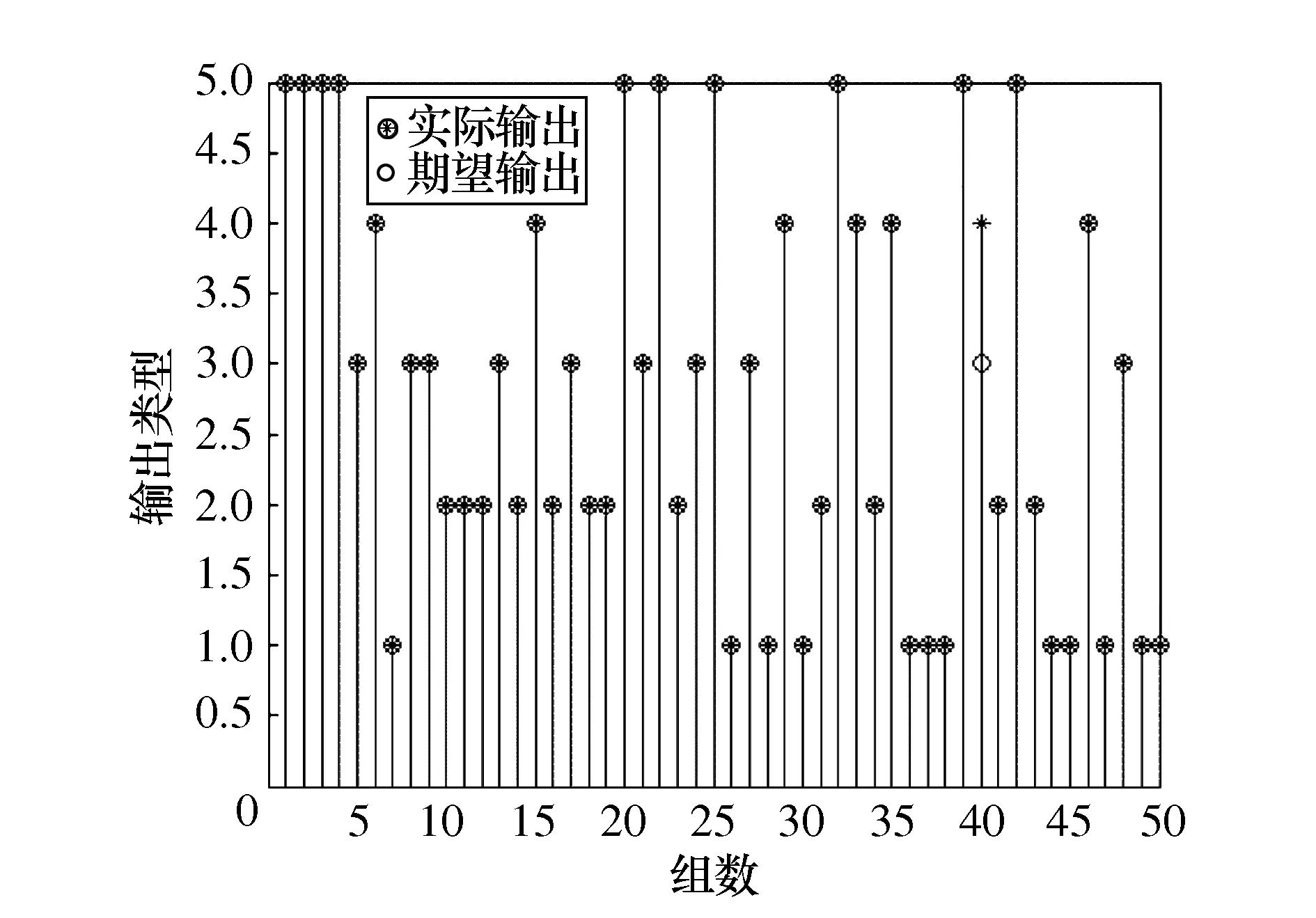
图8 故障诊断结果

4 结论

1) 通过判断引起湿式离合器换段不理想的液压系统故障类型,采用AMESim建模,模拟注入不同的故障类型,仿真湿式离合器换段状态下的输入输出轴实际转速差变化,得到该状态下的压力及流量的故障数据,采用时域特征提取方法,对数据进行5个方面的特征提取,得到的特征参数作为神经网络的输入,仿真模型的数据涵盖了不同程度的故障,能够很好的作为故障诊断系统的数据来源。

2) 针对传统PSO算法容易陷入局部最优解以及预测收敛精度不准的问题,采用QPSO优化BP神经网络对建立的故障诊断系统进行故障预测,该方法比传统PSO优化BP神经网络具有更加精确的预测精度,且具有更好的收敛效果。

3) 通过台架的故障实际模拟,利用仿真试验得到优化后的权值、阈值矩阵作为QPSO-BP的初始化参数,提升了台架故障预测的预测效率,系统运行时间为31.0128 s,预测精度为98%。通过仿真模型来获取数据并训练,再用台架数据验证,这种方法更加高效,便捷,避免了试验过程中由于故障程度的不同带来模拟试验数据集过小的问题,该方法为 HMCVT故障诊断系统工程应用提供算法依据和新的开发思路。