并联式加注机器人鲁棒轨迹跟踪控制

赵 纯，于存贵，徐 华，徐 强

（1. 南京理工大学，南京，210094；2. 上海宇航系统工程研究所，上海，201108）

0 引 言

运载火箭燃料加注的自动化是实现火箭安全发射的重要前提。考虑到加注机器人需安装在发射架摆杆上，同时需承载管路和燃料的质量，因此需具备高功质比、承载力强、动态性能好等特性。液压驱动型并联机器人满足以上所有特性要求。

并联机器人虽具有以上诸多优点，但是由于其本质上是一个多变量耦合的机械系统，其高性能控制仍是一个难点。目前针对并联机器人的控制策略主要分为两类。一类是基于分散控制方法的策略，其主要针对各个关节进行算法设计，把并联机构的动力学耦合干扰当作各关节的一项扰动进行处理，通过设计关节扰动观测器进行补偿控制。该类方法具有无需建模、算法结构简单的优点，但是其控制精度主要在于其观测器精度，对于瞬时强干扰，有可能造成系统的失稳。另一类是基于动力学模型的控制策略。目前，自适应控制、滑模控制、智能控制算法都得到了广泛应用。鲁棒控制策略从设计上来说，虽然具有一定的保守性，但是具有算法简单、稳定性好的优点，目前也得到了广泛的研究与应用。

本文以某液压驱动型并联式加注机器人为研究对象。首先建立包含并联机器人和液压驱动器动态特性的系统高阶多输入多输出模型。其次，基于反步方法设计一种加注机器人高精度鲁棒控制器，并通过Lyapunov 方法证明其稳定性。仿真结果表明，该控制器有较高的轨迹跟踪精度，能够满足实际加注场合的对接应用需求。

1 系统建模与问题描述

对于受风载作用的火箭箭体，其运动主要集中在3个平动自由度，而在3 个转动自由度上的运动量较小(不大于0.5°)。因此，自动加注机器人设计为三平动并联机构串联六自由度柔顺机构的混联结构方案，其总体结构如图1 所示。

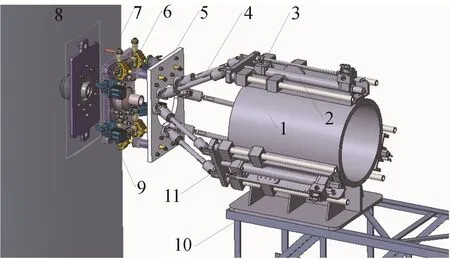
图1 并联式加注机器人结构示意Fig.1 Structural Diagram of Parallel Filling Robot

1.1 柔顺机构等效刚度模型

柔顺机构的运动简图与等效刚度模型见图2，主要用于补偿三平动并联机器人在空间六自由度上的对接误差。

图2 柔顺机构运动简图与结构等效刚度示意Fig.2 Kinematic Diagram of Compliant Mechanism and Schematic Diagram of Structural Equivalent Stiffness

柔顺机构具有六自由度的空间位姿补偿能力，但在实际加注任务中，箭体3 个偏转自由度幅值较小,因此柔顺机构在空间三平动自由度上近似解耦，其等效刚度模型如下：

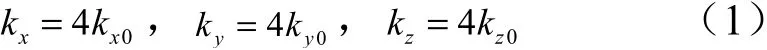
式中k、k和k分别是左右、上下和前后支链中单个弹簧的刚度系数。

1.2 3-PSS 并联机构动力学建模

3-PSS 机构结构简化单杆等效模型见图3。

图3 3-PSS 机构结构Fig.3 Structure Diagram of 3-PSS Mechanism

在基座和动平台中心点分别建立固定参考坐标系和连体参考坐标系。3-PSS 机构的动力学模型有如下形式：

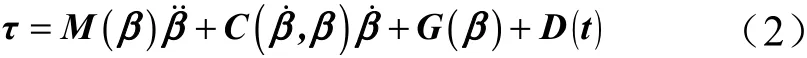
式中=[,,]为在固定坐标系中的位置矢量；()为惯性矩阵；(, ˙)为哥氏力和离心力矩阵；()为重力矢量；()为系统建模误差和外部干扰；为系统的驱动力矢量。

式（2）描述的动力学系统具有如下性质：

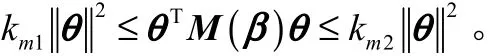
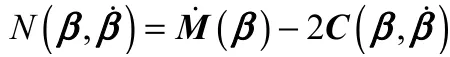
1.3 液压驱动器建模

液压驱动器的结构原理如图4 所示。

图4 液压驱动器原理Fig.4 Schematic Diagram of Hydraulic Actuator

驱动器的动态模型可以有如下表示：

式中q和q为液压缸的输出位移和速度；m为活塞杆和负载质量；d为液压缸的不匹配不确定误差；τ为驱动力；u为控制输入；d为液压缸的匹配不确定误差。

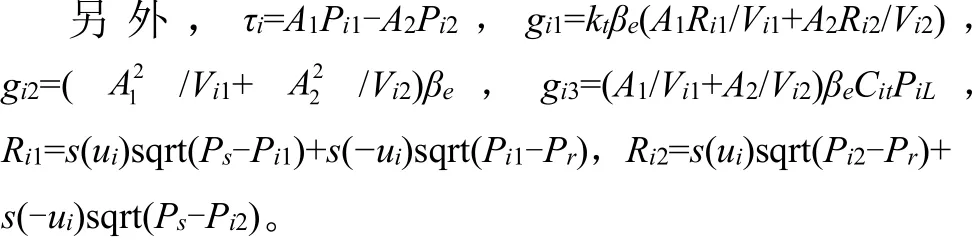
式中P和P为液压缸两腔压力；和为液压缸两腔的有效面积。V，V分别为两腔有效容积，V=V+q，V=V-q，其中V和V为其初始容积；β为油液弹性模量；C为内泄漏系数；P=P-P为两腔压差；为总的流量增益；为供油压力；为回油压力。(x)={1, ifx≥0; 0, ifx＜0}。

1.4 系统完整动力学模型

综合式（2）和（3），可得系统完整的动态模型为

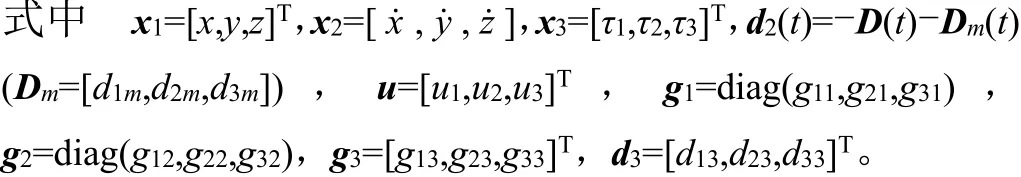
为了便于控制器设计，有如下假设：

假设1：液压驱动器在常规工况下工作，即有0＜P＜P＜P，0＜P＜P＜P。

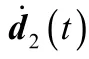
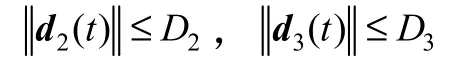
式中，均为大小已知的正数。

2 控制律设计

2.1 反步鲁棒控制器设计

步骤1：定义为笛卡尔空间期望轨迹，=-。对求导得：

定义虚拟控制量：

式中为正定对角矩阵。

步骤2：定义动态误差=-，则有：

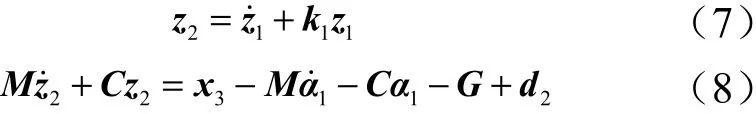
为设计一个如下形式的虚拟控制函数：

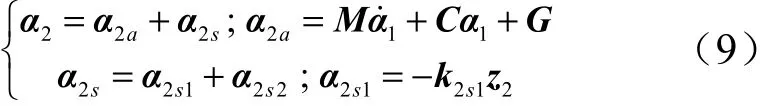
式中为系统的名义模型补偿项；为鲁棒控制项；为正定对角矩阵。

定义=-，同时将式（9）代入（8），可得：

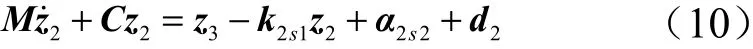
设计满足如下的镇定条件：

式中 ε为可任意小的正数。

令≥，则满足条件（11）的可以设计为

式中为正定非线性增益矩阵，为三阶单位阵。

步骤3：对求导可得：

因此，期望控制律可以设计为

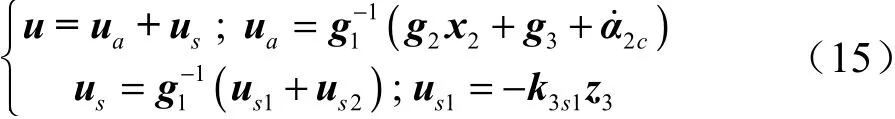
式中u为模型补偿控制项，u为鲁棒控制律，为正定对角矩阵。

将式（15）代入（13）可得：

设计u满足如下的镇定条件：

式中为可任意小的正数。

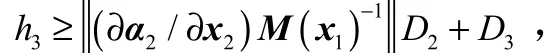
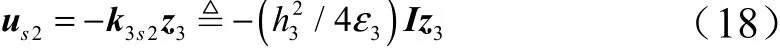
2.2 稳定性分析

定义系统Lyapunov 函数为

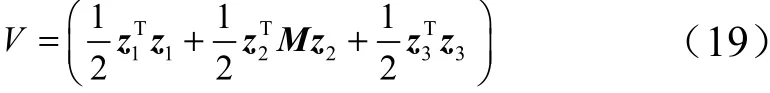
对式（19）两端求导可得：

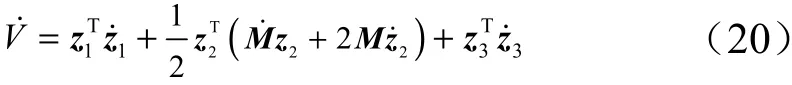
针对上式，同时注意到性质2，有：

结合式（5）、（7）、（16）、（20）和（21），可得：

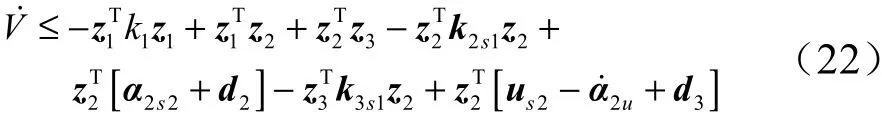
注意到式（11）和（17），因此有：

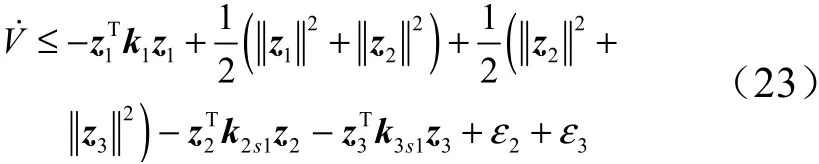
定义=()，=()，=()分别为正定对角矩阵1、21和31的最小特征值。因此有：

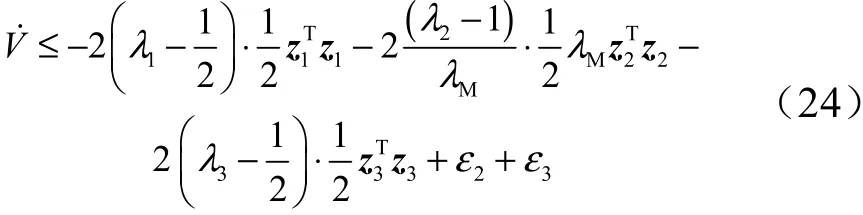
式中=()为矩阵的最大特征值。

考虑到性质1，由（25）可得：

定义=+，根据对比原理有：

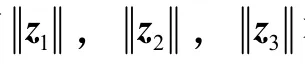
2.3 期望轨迹生成

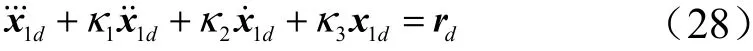
式中、和分别为滤波器系数。

3 仿真分析

3.1 系统模型参数和控制器参数

针对并联机器人，有OA=0.32 m，O’B=0.14 m，连杆长度=0.45 m，动平台及负载质量m=35 kg，连杆质量m=9.8 kg，连杆转动惯量I=I=I=0.2 kg·m，导向杆质量m=22 kg，综合弹簧刚度k=k=k=15 N/mm。

针对液压驱动器，有m=3 kg，A=1.25×10m，A=6.4×10m，β=2×10Pa，P=10 MPa，P=0，C=9×10m/s/Pa，k=4×10m/s/V/ Pa，V=1.2×10m，V=2.96×10m。

仿真步长设置为0.5 ms。为了更好的验证控制器性能，针对以下两种控制器进行仿真对比分析。

a）基于动力学模型的鲁棒控制器(Model-based Robust Control ， MRC) 。 控 制 器 参 数 设 计 为=diag{1000,1000,1000}，=+=diag(800,800,800)，=+=diag(500,500,500)，三阶滤波器的系数为=12500，=7500，=150。

b）速度前馈PID 控制器(VFPID)。控制器参数设计为：k=1200，k=600，k=2，k=10V·s/m。

3.2 仿真分析

加注机器人的加注任务可分为两个阶段的运动：对接保持阶段和随动脱落阶段。

3.2.1 工况1：对接保持阶段工况仿真

该阶段加注机器人与火箭箭体均处于封闭的发射塔架中，此时不受风载的作用，对接任务可以简化为动平台中心点一个点到点的运动。

箭/地连接器面板的对接过程示意如图5 所示。

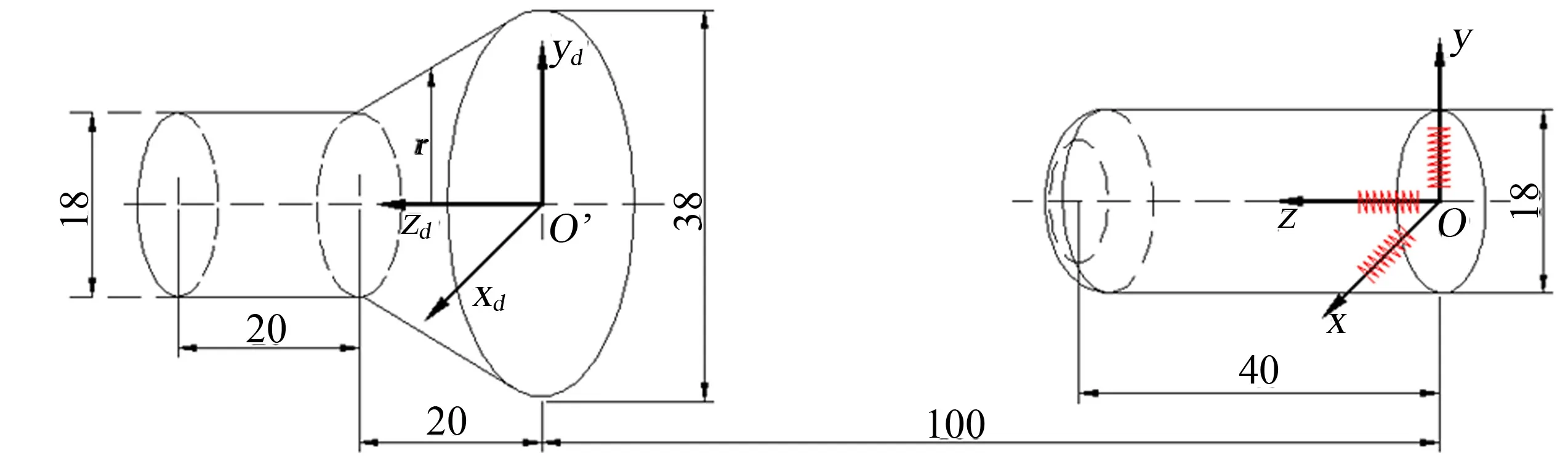
图5 对接导向杆与导向孔相对状态示意Fig.5 Schematic Diagram of Relative State of Guide Rod and Guide Hole

假设面板间的初始距离为100 mm，对接速度为10 mm/s，因此对接轨迹r可以设计为

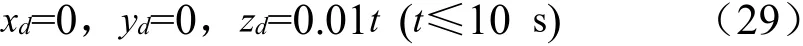
加注机器人受到的外部干扰主要由导向杆/孔对接误差引起的柔顺机构弹簧形变力。在≥98mm 时，锁紧机构完成箭/地面板的锁紧。同时，假设导向杆/孔的接触运动是顺滑的，则根据杆/孔的相对位置可以定义出箭体对加注机器人的干扰力为

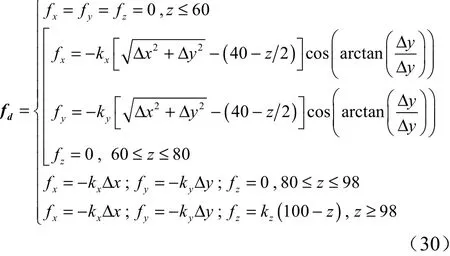
式中 △，△，△分别为加注机器人在笛卡尔空间的对接跟踪误差，△=-x，△=-y，△=-z。

由于整个对接过程加注机器人的运动速度都较为缓慢，因此其建模误差项可以认为是一恒值扰动，假设该扰动为

结合式（30）和（31），式（4）中的系统中干扰项()可以定义为

图6、图7 为MRC 和VFPID 两种算法对于低速运动期望轨迹的跟踪情况。仿真结果表明，MRC 和VFPID 这两种算法对于低速运动皆表现出较高的轨迹跟踪精度，同时MRC 控制器相对VFPID 控制器轨迹跟踪性能更优。

图6 MRC 空间跟踪误差Fig.6 Tracking Errors in Workspace of MRC

图7 VFPID 空间跟踪误差Fig.7 Tracking Errors in Workspace of VFPID

此外，在接近=10s 处，由于轨迹过渡和锁紧机构锁紧力的引入，使得两种控制器均有跟踪误差一定的放大，但是MRC 控制器误差的波动明显小于VFPID。由此可见，VFPID 虽然具有一定的抗干扰能力，但是其本质上是一种无模型控制算法，其对扰动的响应总是起作用于误差发生之后，因此当瞬时扰动(轴向锁紧力)产生时，其缺少快速响应的能力，从而造成跟踪误差相对较大的恶化。

3.2.2 工况2：随动脱落阶段工况仿真

该阶段发射塔架打开，当接收到脱落指令后，加注机器人需完成在随动过程中的3 s 脱落任务，此时箭体因风载作用会有小幅摆动行为。考虑到箭体受左右风载时，其运动状态最为恶劣，因此针对该工况进行仿真。假设箭体摆动为x=0.05sin(π)，在=10 s 时接收到脱落指令。因此，可将动平台中心点的期望轨迹设计为

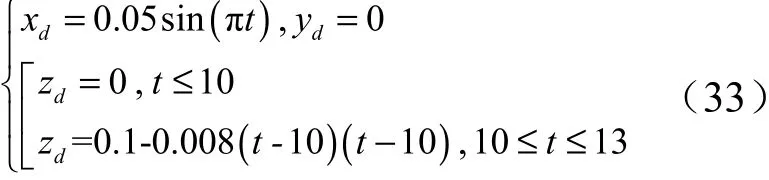
箭体对加注机器人施加的干扰力可以定义为

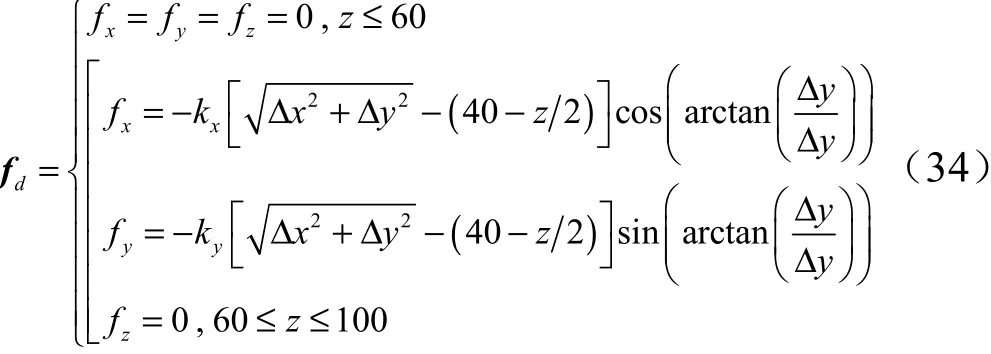
考虑到加注机器人在动态运动时，其建模误差将是一个时变的动态量，因此定义该动态误差为

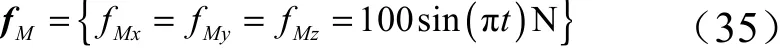
结合式（33）和式（34），式（4）中的()定义为

仿真结果如图8 和图9 所示。

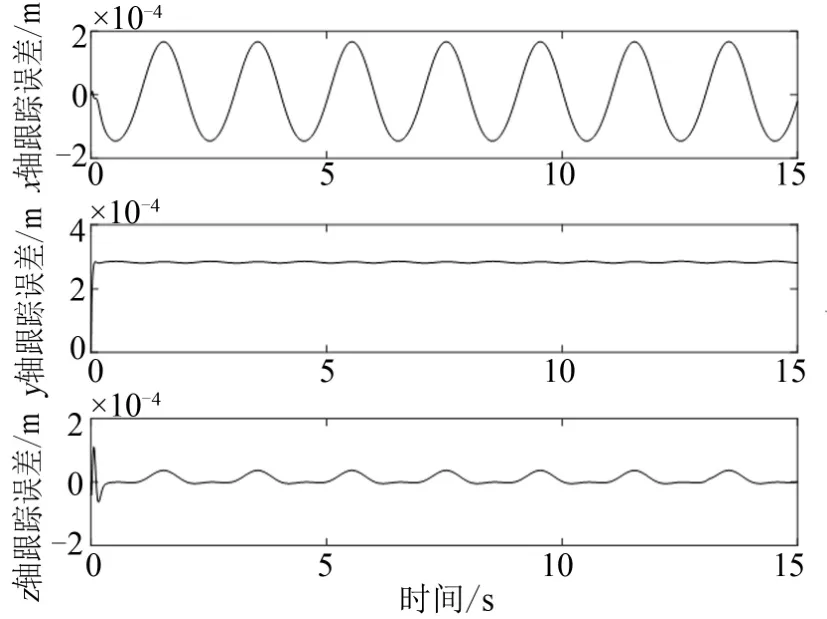
图8 MRC 空间跟踪误差Fig.8 Tracking Errors in Workspace of MRC

图9 VFPID 空间跟踪误差Fig.9 Tracking Errors in Workspace of VFPID

结果表明，对于随动脱落工况，两种控制器的跟踪误差均有一定的放大，但得益于系统较好的抗干扰能力，MRC 的控制性能仍远优于VFPID。同时，注意到在脱落阶段=(10~13) s，两种控制器并未表现出明显的轨迹跟踪性能恶化的情况，一方面这是由于脱落轨迹在设计时已经考虑到整个脱落过程的平滑性问题，即在=10 s 处对脱落原轨迹做了过渡处理；另一方面轨迹初始化技术的引入进一步保证了系统的暂态性能。

4 结 论

通过理论和仿真分析，得到了如下成果：

a）建立了包含并联机器人和液压驱动器动态特性的加注机器人完整的高阶多输入多输出模型。针对系统中存在的建模误差和外界干扰，设计了一种具有扰动抑制能力的高性能鲁棒控制策略；

b）结合加注任务剖面，完成了对接轨迹设计和加注过程扰动建模，对加注过程进行了完整的仿真分析。仿真结果表明，鲁棒控制器相较传统PID 式控制器具有更强的轨迹跟踪性能和抗干扰能力。

本文的研究成果对后续原理样机的研究开展具有较强的参考价值，同时对其它并联机器人的控制器设计同样具有一定的借鉴意义。