电静压伺服系统指数型变阻尼滑模控制算法研究
2022-06-27高诗程赵守军张春龙
高诗程,张 朋,赵守军,张春龙,冯 伟
(北京精密机电控制设备研究所,北京,100076)
0 引 言
电静压伺服系统(Electro-hydrostatic Actuator,EHA)兼具固有可靠性高和易维护等突出优点,是未来多电化、高可靠火箭推力矢量控制系统的主流作动器方案。
但传统上认为EHA 本质是一个泵控系统,其动态特性较差,频率特性不如阀控伺服,难以满足运载火箭要求。张玉强采用“比例+陷波补偿”算法进行控制,与阀控系统动态性能进行了对比分析,动态性能基本满足火箭发动机控制需求。刘璐采用“非线性PID+前馈补偿+陷波补偿”组合算法进行控制,动态特性进一步提升,达到同等电液伺服的动态技术水平,已满足运载火箭需要。为进一步挖掘电静压伺服系统的动态特性潜能,提升控制指标裕量,仍需开展更先进的控制算法研究。
近年来,针对EHA 的高性能控制策略设计,国内外许多学者在改进PID 控制、智能控制、模糊控制、滑模控制等方面开展了研究,取得了一定的成果。其中,滑模控制作为一种非线性控制方法,能够有效应对系统的外部干扰与内部参数时变性,且其结构简单、容易实现,是目前研究的热点控制策略之一。张英臣等在EHA 位置环采用滑模控制,在满足快速性的情况下,超调量减小,系统获得较高频宽。洪辉等同样在位置环采用滑模变结构控制,并采用自适应遗传算法进行参数优化,有效减小系统超调,提高快速性,减小系统静差。但张英臣等和洪辉等只给出了仿真分析,未提供试验数据。Wang M. K.等提出了一种反正切函数导数型变阻尼滑模控制算法,根据位置误差调节滑模面阻尼比,在保证系统快速性的同时抑制了超调现象,但只给出了阶跃和1 Hz 正弦指令的响应特性,对实际应用中最关注的频率特性未给出仿真和试验结果。
提出指数型变阻尼滑模控制算法,以指数函数形式调节滑模面阻尼比,平衡系统快速性与平滑性之间的矛盾。同时,引入基于正切Sigmoid 函数的跟踪微分器获取平滑的反馈速度信号,有效改善滑模算法的控制稳定性。此外,本文也针对工程适用的电静压伺服系统传递函数模型,给出了对应的状态方程及滑模算法。
建立了系统模型,搭建了试验平台,通过系统仿真及EHA 工程样机的带载试验,验证了控制算法的合理性和可行性。结果表明,相比于基于前馈的非线性PID 控制算法,在系统基础开环增益取20 rad/s 的情况下,指数型变阻尼滑模算法在系统低频段跟踪精度提升1 倍,-45°相频宽由18.4 rad/s 提升至29.6 rad/s。
1 系统及控制模型
EHA 主要由控制器、驱动器、伺服电机泵、位移传感器、作动器和负载组成。工作原理如图1 所示。根据输入指令,控制器通过驱动器控制电机的转速和转向来控制电机泵输出流量的方向和大小,进而控制作动器活塞杆的运动方向和速度。

图1 EHA工作原理Fig.1 Simplified Schematics of an EHA
EHA 基本组成如图2 所示。

图2 EHA 基本组成Fig.2 Block Diagram of an EHA
EHA 系统设计主要参数如表1 所示。
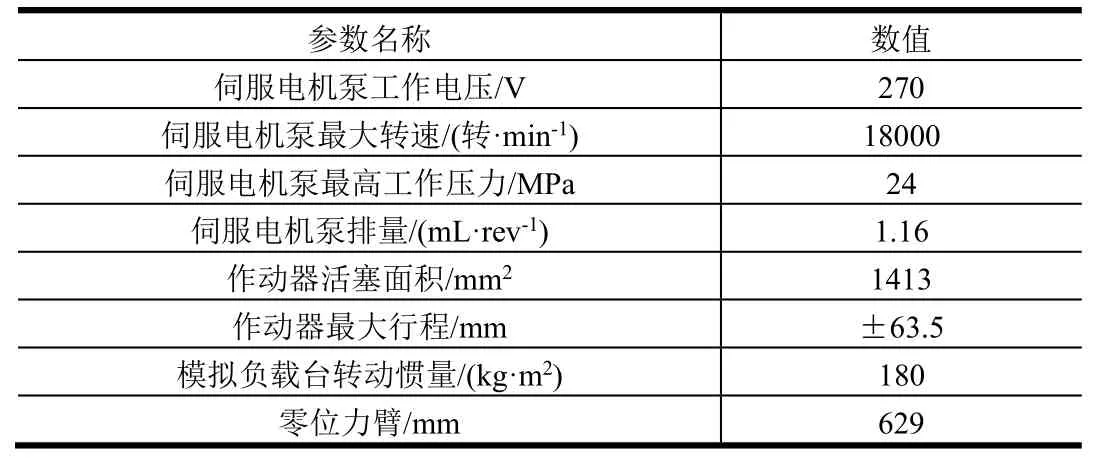
表1 EHA 基本设计参数表Tab.1 Main Design Parameters
作动器及负载简化模型如图3 所示。负载简化为一个质量体和一个与作动器连接的弹簧,表示运载火箭大推力发动机的谐振特性。

图3 作动器及负载模型Fig.3 The Physical Model of an EHA to Drive an Engine Load
系统数学模型表示为

式中为电机泵等效二阶环节传递函数;为电机泵等效二阶环节增益;为电机泵等效二阶环节无阻尼自然振荡频率;为电机泵等效二阶环节阻尼比;为柱塞泵排量;为作动器总泄漏系数;为作动器液压缸两腔总体积;为液体体积弹性模量;为负载转动惯量;为伺服机构摇摆负载力臂;为负载结构谐振频率;为负载结构等效阻尼;为液压固有频率;c为机械液压综合谐振频率;为机械液压综合谐振阻尼比;为位移反馈系数;为基础开环增益。
伺服电机为永磁同步电机,采用=0 的控制方式,电流环和转速环采用PI 控制,本文关注系统的中低频段,且关注系统位置环的控制策略,因此将电机泵等效为一个二阶环节。
由式(1)~(11)可得EHA 位置闭环规范化框图,如图4 所示。作动器及负载部分进行等效化简,将其简化为负载特性环节与负载效应环节。其中,,,r及都可在线辨识,因此相比以物理参数表达的模型实用性更好。图4 中饱和环节表示电机驱动器的电流能力,由于此饱和限制,直接采用增大增益的方法,系统动态性能通常提升有限。因此采用非线性控制算法,增大小误差信号时的增益,减小大误差信号时的增益,从而提高动态品质。而滑模算法本质是一类特殊的非线性控制,系统处于滑动模态时,对外部的干扰具有很好的鲁棒性,通过滑模面的设计,可获得系统期望的动态品质,且控制算法简单,易于工程实现。

图4 EHA 位置闭环控制规范化框图Fig.4 Normalized Block Diagram of an EHA
2 指数型变阻尼滑模控制算法
2.1 系统状态方程
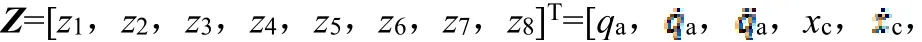
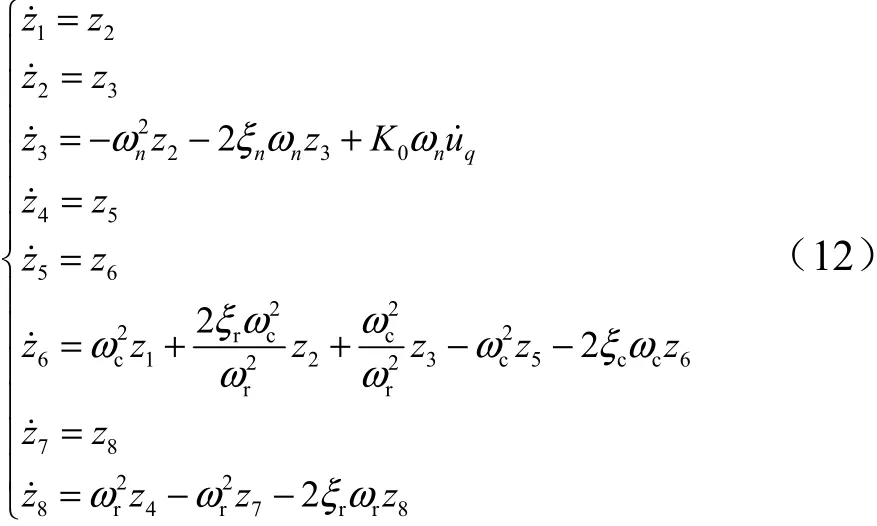
实际使用中,更关注系统中低频段,忽略表达电机环节动态特性的、,同时考虑在闭环内设计算法,去掉闭环外的、,剩余、、、项,选择作为输入项,令=[,,]=[,,]=[,,],修正后状态方程如式(13)所示:

2.2 常规滑模控制算法
取EHA 位移指令与反馈的误差及其导数作为滑模控制算法的误差向量。
跟踪误差如式(14)所示:

设计常规二阶线性滑模面,如式(15)所示:

其中:,>0 ,满足Hurwitz 条件。
由状态方程式(13)变换形式得到活塞位移三阶微分项˙˙˙,如式(16)所示:
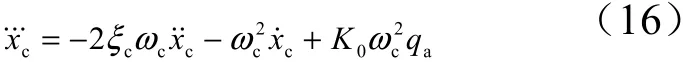
采用指数趋近律,如式(17)所示:

式中为开关函数系数;为滑模面系数。
对式(15)求导,并与式(16)一同代入式(17),得到基于指数趋近律的滑模算法,如式(18)所示:
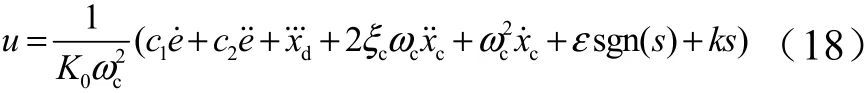
式中为滑模控制器输出量。
取Lyapunov 函数,如式(19)所示:

对式(19)求导,并将式(17)代入得到式(20):

由此可知,滑模面满足存在性和可达性,系统稳定。
2.3 变阻尼滑模控制算法
滑模控制算法性能很大程度上取决于滑模面,故滑模面设计与选择成为滑模控制器设计中最为关键的问题。式(15)表示的滑模面中包含、两个参数,将二阶线性滑模面等效为标准二阶振荡环节,其取值将影响到系统响应的快速性与平滑性。
对式(15)改进,采用指数型变阻尼滑模面,如式(21)所示:

式中为滑模面无阻尼固有频率;( )为变阻尼函数;和为最小阻尼比和最大阻尼比;为用于调节变阻尼变化快慢的敏感因子。
由式(21)可知,在滑动阶段初期,系统位置误差较大,阻尼比较小,趋近于,使系统快速趋向滑模面。随着位置误差减小,阻尼比逐渐增大,阻尼比趋近于+,使系统到达滑模面时超调量较小。变阻尼敏感因子则影响实际阻尼比趋近最大最小值的速度。与反正切函数导数型变阻尼滑模面相比,指数型变阻尼滑模面在小误差时阻尼比变化更为迅速,同样在大误差时衰减更快,从而实现更优的调节能力。
不同敏感因子下的指数型阻尼比曲线如图5所示。
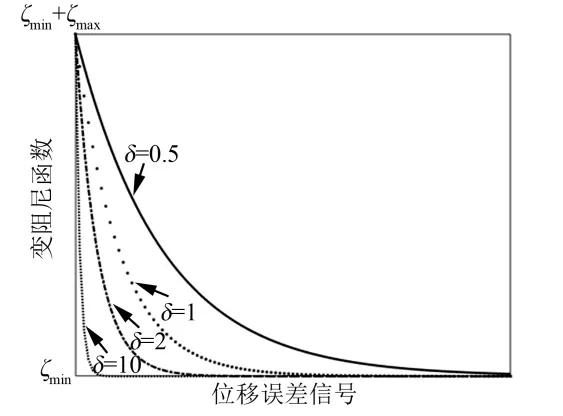
图5 指数型变阻尼曲线Fig.5 Exponential Variable Damp Curve
图5中,当=1 时,变阻尼曲线小误差和大误差情况下敏感程度适中,因此本文取=1 进行研究。
将常规滑模控制算法式(18)修正为变阻尼滑模控制算法,如式(22)所示:
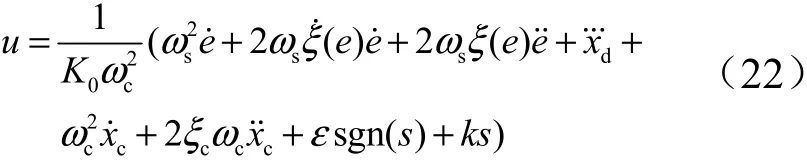
针对所关注的中低频段,一阶微分已足够满足系统控制需求,故省略控制算法中的二阶及以上微分项,修正后的变阻尼滑模控制算法,如式(23)所示:
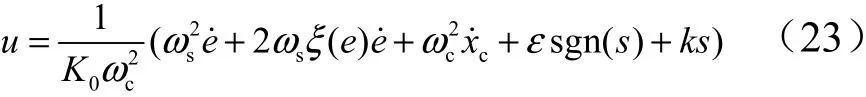
2.4 跟踪微分器
根据变阻尼滑模控制算法可知,反馈通道中速度信号的求解至关重要,一般采用位置微分得到速度信号,而工程中因噪声等因素,兼顾响应速度和平稳性有困难,不平滑的反馈速度信号会降低系统的稳定性。因此引入跟踪微分器获取反馈通道中的速度信号。
跟踪微分器是对加速度信号进行数值积分求取速度信号,相比于工程中常用的差分法,能够较好地滤除噪声。本文采用正切Sigmoid 函数改进加速度函数,其形式如式(24)所示:
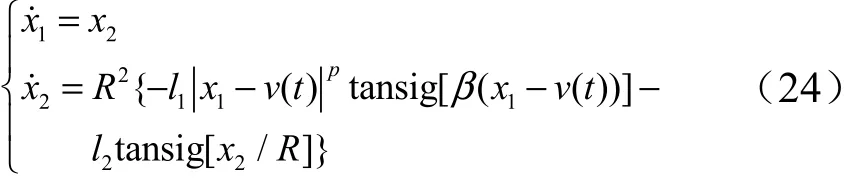
式中为微分器计算位移值;为微分器计算速度值;() 为反馈通道实际位移信号;为微分器主增益;为终端吸引子函数系数;为正切Sigmoid 函数指数因子;,为正切Sigmoid 函数幅值增益。
3 仿真分析
刘璐提出了“非线性PID+前馈+陷波”组合控制算法,其结构如图6 所示。
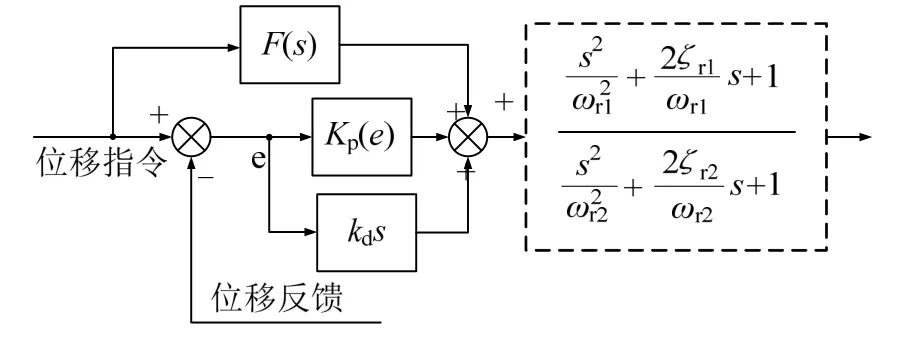
图6 组合控制算法结构Fig.6 Schematics of the Combined Control Algorithm
其中,比例增益和前馈环节表达如式(25)所示:
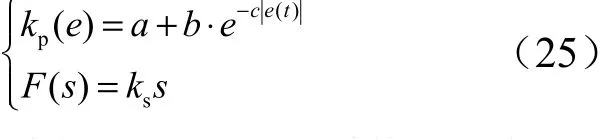
式中,,为非线性PID 比例项系数;为非线性PID 微分项系数;为前馈系数;为陷波器零点频率;为陷波器零点阻尼比;为陷波器极点频率;r为陷波器极点阻尼比。
不失一般性,为简化分析,本文仿真分析不考虑陷波器,在试验时系统基础开环增益取较小的20 rad/s,输入取小幅值信号,保证系统在谐振时的安全性;在实际使用时,直接在算法中增加陷波器即可。系统模型参数如表2 所示,基于前馈的非线性PID 控制算法参数如表3 所示,滑模控制算法参数如表4 所示。

表2 EHA 模型参数表Tab.2 Parameters for Normalized Transfer Function

表3 组合控制算法参数表Tab.3 Parameters for Combined Control Algorithm
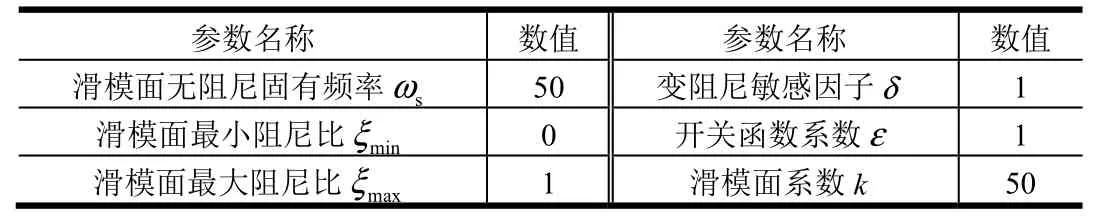
表4 滑模控制算法参数表Tab.4 Parameters for Sliding Mode Control Algorithm
3.1 位置跟踪仿真
给定系统幅值6 mm(约满量程10%),频率1 Hz的正弦位置信号,负载端角位移位置跟踪曲线见图7。

图7 正弦跟踪仿真曲线Fig.7 Simulated Sinusoidal Tracking Curve
由图7 可知,跟踪曲线幅值不超调的情况下,采用基于前馈的非线性 PID 算法跟踪最大误差为1.35 mm,相位滞后为-14.18°;而采用指数型变阻尼滑模算法跟踪最大误差为 0.53 mm,相位滞后为-6.34°,跟踪精度提高一倍,相位滞后减小约55%。
3.2 频率特性仿真
给定幅值3 mm(约满量程5%)、频率1~150 rad/s的正弦扫频信号,负载端角位移频率特性如图8 所示。
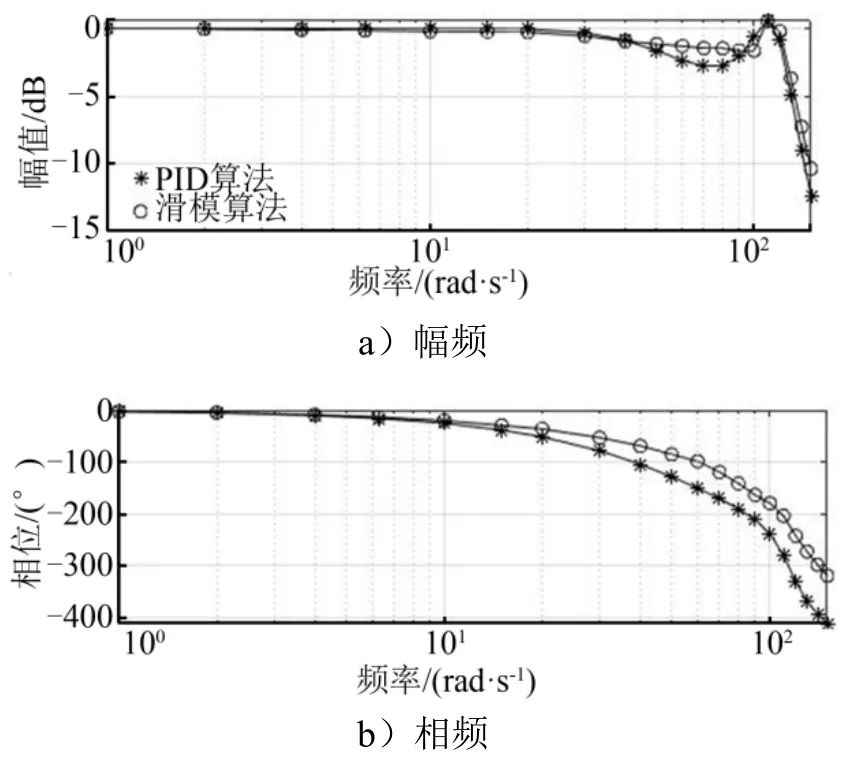
图8 频率特性仿真曲线Fig.8 Simulated Frequency Response Curve
由图8 可知,基于前馈的非线性PID 算法-45°相频宽为20.2 rad/s,而指数型变阻尼滑模算法-45°相频宽提升至30.8 rad/s,幅频曲线在中高频段幅值衰减更小,系统谐振峰值也并未增大,相频提升明显。
由仿真结果可知,由于图4 中饱和环节的存在,基于前馈的非线性PID 算法难以协调全频段中快速性与平稳性的矛盾,对于相频提升仍然有限。而滑模控制算法对于内部参数变化不敏感,能够根据控制要求设计合适的滑动模态,通过设计趋近律保证系统在有限时间内到达滑模面,使系统在保证平稳的同时进一步提高快速性,而加入指数型变阻尼滑模面之后,调节更加精细,因此提高了系统的动态性能。
4 试验研究
4.1 试验设计
搭建EHA 试验平台,系统组成如图9 所示,其中测试仪用来发送指令并记录采集数据,控制器根据位置闭环控制算法计算转速指令,驱动器根据电机转速指令控制伺服电机泵,从而控制作动器动作。
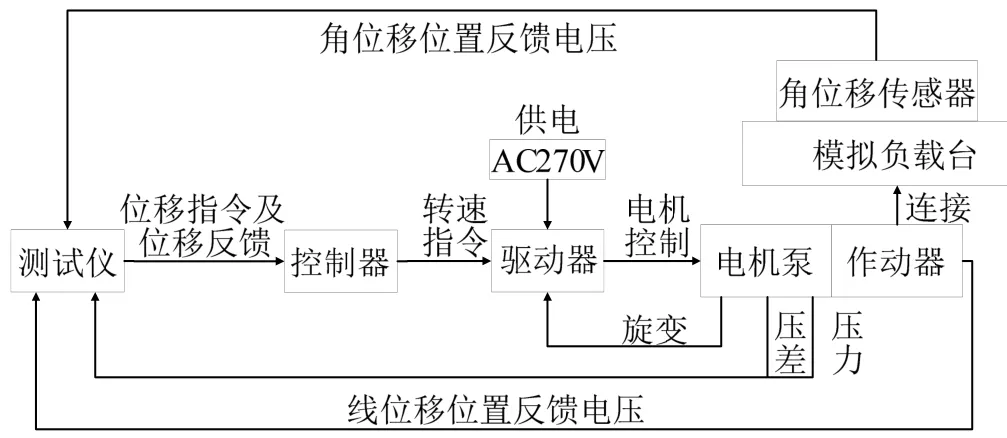
图9 试验系统组成原理Fig.9 Block Diagram of the Experiment System
EHA 负载对象以惯性负载为主,试验测试等效原理及实物如图10 所示。

图10 带载测试等效原理及实物Fig.10 Simplified Schematics and Photo of the Loaded EHA Test System
由试验数据得到系统负载结构特性见图11。由拟合数据得到负载结构谐振频率为110 rad/s,负载结构谐振阻尼比为0.097。
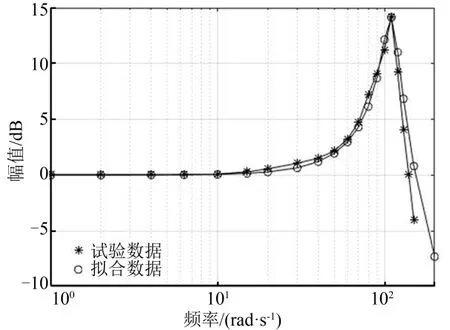
图11 负载结构特性Fig.11 The Structural Dynamics of the Load
4.2 位置跟踪试验
给定系统幅值6 mm(约满量程10%),频率1 Hz的正弦位置信号,负载端角位移输出曲线如图12所示。由图12 可知,系统位置跟踪在不衰减的情况下,采用指数型变阻尼滑模算法相比于基于前馈的非线性PID算法,其跟踪最大误差由2.18 mm 减小至1.01 mm,同时相位滞后也由-18.72°减小至-8.6°。由此可知,相比于基于前馈的非线性PID 算法,在系统的位置环采用指数型变阻尼滑模算法有效提高了系统的低频段位置跟踪精度。需要说明的是,实际系统中存在摩擦、间隙等非线性因素,与仿真相比跟踪误差及相位滞后均稍大,但改进的效果清晰。

图12 正弦跟踪曲线Fig.12 Sinusoidal Tracking Curve
4.3 频率特性试验
对系统进行频率特性试验测试,输入幅值3 mm(约满量程5%)、频率1~150 rad/s 的正弦扫频信号,得到负载端角位移频率特性如图13 所示。由图13 可知,两种算法幅频曲线基本重合,指数型变阻尼滑模算法的相频较基于前馈的非线性PID 算法有较大提升,-45°相频宽从18.4 rad/s 提升至29.6 rad/s,且高频段谐振峰值并未增大。表明指数型变阻尼滑模算法相比于基于前馈的非线性PID 算法有效改善了系统相位滞后问题,提高了系统动态性能。

图13 频率特性曲线Fig.13 Frequency Response Curve
5 结束语
本文针对EHA 的高动态响应问题,提出了一种指数型变阻尼滑模控制算法,同时采用基于正切Sigmoid函数的跟踪微分器,实现了反馈通道中平滑速度信号的获取。仿真及试验结果表明,指数型变阻尼滑模算法能够有效提高系统在低频段跟踪精度,显著提升系统相频频宽,提高系统快速性,进一步改善系统相位滞后的问题。
