惯性稳定平台自适应分数阶参数寻优方法
2022-06-27赵国新
李 晶,于 沛,赵国新,马 丹
(1. 北京石油化工学院信息工程学院,北京,102617;2. 北京航天控制仪器研究所,北京,100039;3. 中国消防救援学院,北京,102202)
0 引 言
惯性平台系统的惯性测量装置安装在台体上,台体通过框架安装在载体上,敏感角运动的陀螺仪所建立的基准轴系通过稳定回路控制框架运动,使台体在载体运动中始终保持与初始建立坐标系重合。对于惯性平台系统,稳定回路的控制精度直接影响着惯性器件在惯性平台系统发挥的精度水平,尤其是在国防技术领域,惯性平台的精度基本上决定了弹道导弹的命中精度。
惯性平台稳定系统属于镇定系统,它可以抵御外部的干扰力矩,使平台轴保持原来状态。目前,惯性平台系统中控制器广泛采用经典频率域控制器的设计方法。随着控制技术的发展,许多学者将一些新型的控制理论和控制方法在惯性平台系统中进行应用研究,目的是提高惯性平台系统的精度、鲁棒性、可靠性、环境适应性以及满足小型化等需求。
近年来相关领域学者根据控制理论的进展将控制理论的研究成功应用于稳定回路的控制中。国外方面,B. Yuri 采用滑模变结构控制方案提高了由动力调谐陀螺组成的三轴惯性稳定平台的控制精度,采用非线性函数和非线性动态算子的形式设计局部滑模,使惯性平台稳定系统的每一轴都具有期望的线性解耦输出,分别对三轴惯性平台稳定系统与设计的常规控制器和动态滑模控制器进行仿真,结果表明该控制器的性能有了显著的改善。C. Perez 在二自由度平台控制中采用了基于增益调度的控制器,用以抵抗与载体运动带来的干扰,通过该策略达到期望的性能指标。Koruba 提出了基于动基座的三轴陀螺稳定平台的模型,基于逆动力学使用LQR 方法设计了控制器。中国方面,宋金来等人设计了惯性平台稳定回路的自抗扰控制方法,通过仿真试验表明,自抗扰控制系统具有响应速度快,抗干扰能力强等优良特性。胡悦采用非线性积分滑模控制方法的进行全姿态稳定回路的控制,控制器性能更加优越,但只是停留在仿真阶段,没有在实际平台上进行控制实验。
1 惯性平台稳定回路工作原理
稳定回路工作原理为:当干扰力矩投影作用在平台稳定轴上时,平台绕稳定轴发生偏转产生角速度,平台台体上的陀螺仪敏感到该角速度后发生进动,即陀螺绕其输出轴发生转动,输出轴上的角度传感器将该转动信息转换为电信号后,送至后续电路产生相应的控制信号,平台轴端的力矩电机根据该控制信号产生负反馈平衡力矩,抵消稳定轴上的外干扰力矩作用,进而使平台台体相对于惯性空间保持稳定,即台体始终保持在初始给定的位置上。
可得到稳定回路固有传递函数为
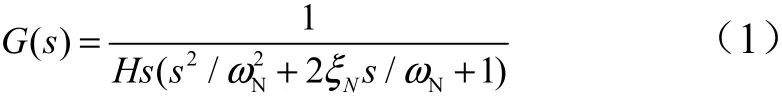
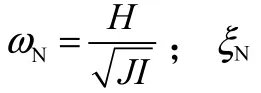
2 惯性平台稳定回路的分数阶控制方法
2.1 分数阶PID 控制方法原理
PID 控制是工业控制系统中最早发展起来的控制策略,由于PID 控制方案并不要求精确的受控对象的数学模型,且采用PID 控制的控制效果令人满意,所以PID 控制器在工业界是应用最广泛的一种控制策略。在传统的PID 控制器中,其微分与积分的阶次都是1,斯洛伐克学者I. Podlubny 教授在1999 年将分数阶微积分的概念引入PID 控制器,提出了PI D控制器的控制结构,其形式更灵活,有望得出更好的控制效果。
分数阶PID 除了与传统的PID 控制器相同的3 个待整定参数,,之外,还有2 个可调参数和。由于和允许为实数,所以控制器参数的整定范围变大。在时域状态下分数阶PID算法的数学表达式为


图2所示为分数阶PID 控制器由整数阶的点变换成分数阶的“面”,参数调节更灵活。
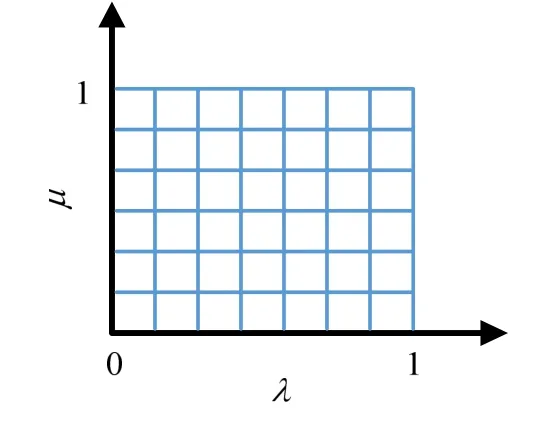
图2 分数阶PID 控制器Fig.2 Fractional Order PID Controller
对Caputo 定义的分数阶微分求Laplace 变换:

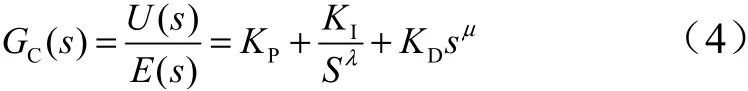
2.2 基于动态惯性权重自适应粒子群参数寻优算法
2.2.1 标准粒子群算法
粒子群算法通过假设一种无质量的粒子来模拟鸟群中的鸟,每个粒子具有两种属性:速度和位置。速度代表该粒子移动的快慢,位置代表粒子移动的方向。每个粒子在搜索空间中单独的搜索最优解,将其记为当前个体最优解;并将当前个体最优解与整个粒子群的其他粒子共享,找到最优的那个个体最优解作为整个粒子群的当前全局最优解;粒子群中的所有粒子根据自己找到的当前个体最优解和整个粒子群共享的当前全局最优解来调整自己的速度和位置。
在维空间中,有个粒子,首先粒子群初始化一群随机粒子,包括速度和位置;粒子位置:x= (x ,x,… ,x),将 x代入适应函数(x)(目标函数)求适应值;粒子速度:v= ( ,v,… ,v)。然后通过迭代找到最优解,每次迭代的过程粒子通过跟踪(,)来更新自己,粒子个体经历过的最好位置:=(p ,p,...p;种群所经历的最好位置:= (,,… ,)。找到这两个最优解后,通过下面公式来更新自己的速度和位置。
粒子的第维速度更新公式为
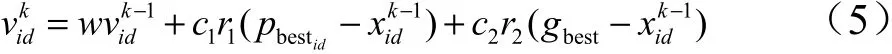
粒子的第维位置更新公式:

标准粒子群算法流程如图3 所示。
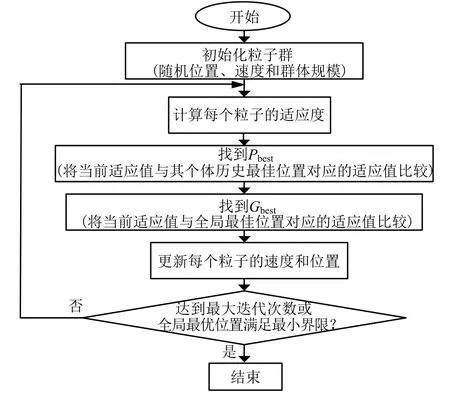
图3 粒子群算法流程Fig.3 Flow Chart of Particle Swarm Optimization
2.2.2 动态权重改进的粒子群算法
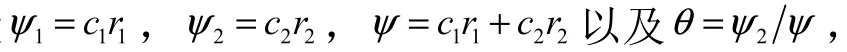
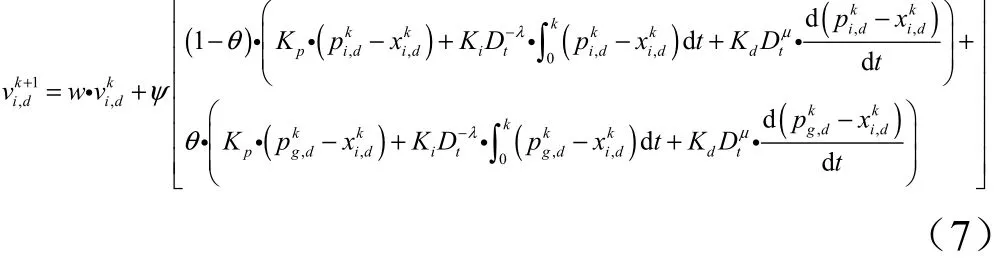
同标准PSO 算法,惯性权重用于控制算法的收敛速度,调节的值就能维持局部搜索和全局搜索的关系。因此,合适的惯性权重能极大的改善算法的最优化能力和减少迭代的次数。一般情况下,通常采用的是线性减少惯性权重,然而,这种方法仅仅适用于在全局最优值附近搜索。本文采用非线性动态惯性权重自适应方法,如下公式所示:

式中,分别为惯性权重的最大值和最小值;为迭代的次数;为迭代的最大次数;,为控制因子。
采用改进PSO 算法整定分数阶PI D 控制器的5 个参数 (,,,,),在综合考虑超调量和控制回路平方误差积分2 个方面因素后,采用如下优化目标函数公式:
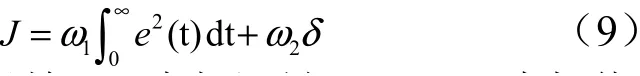
式中() 为系统误差;为超调量;,为权值。
3 仿真试验
采用上节中提出的动态权重改进粒子群算法对稳定平台系统伺服回路分数阶PID控制器的5 个参数(,,,,)进行优化设计,利用Matlab/Simulink 建立稳定平台系统伺服回路分数阶控制器的控制模型,利用Matlab 的M 文件编写动态权重改进粒子群算法,经过反复迭代后得到优化后分数阶PID控制器的5 个参数 (,,,,),其运算过程见图4。

图4 动态权重优化分数阶参数运算流程Fig.4 Dynamic Weight Improved Particle Swarm Optimization Fractional Parameter Operation Flow Chart
采用图4 所示的方法,在Simulink 中进行迭代仿真计算,将迭代次数设置为20 次,可看出在经历4 次迭代后,得到了经过PSO 整定后的PI D 确定了5 个参数。图5、图6 和图7 显示了各种参数与迭代次数之间的关系,可以看出参数的最优值非常小,这是由平台特性决定的,和实际使用情况一致。
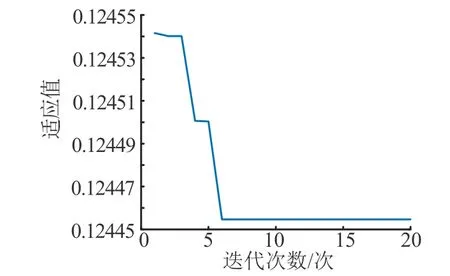
图5 最优个体适应值与迭代次数关系Fig.5 Relationship between the Optimal Individual Fitness Value and the Number of Iterations
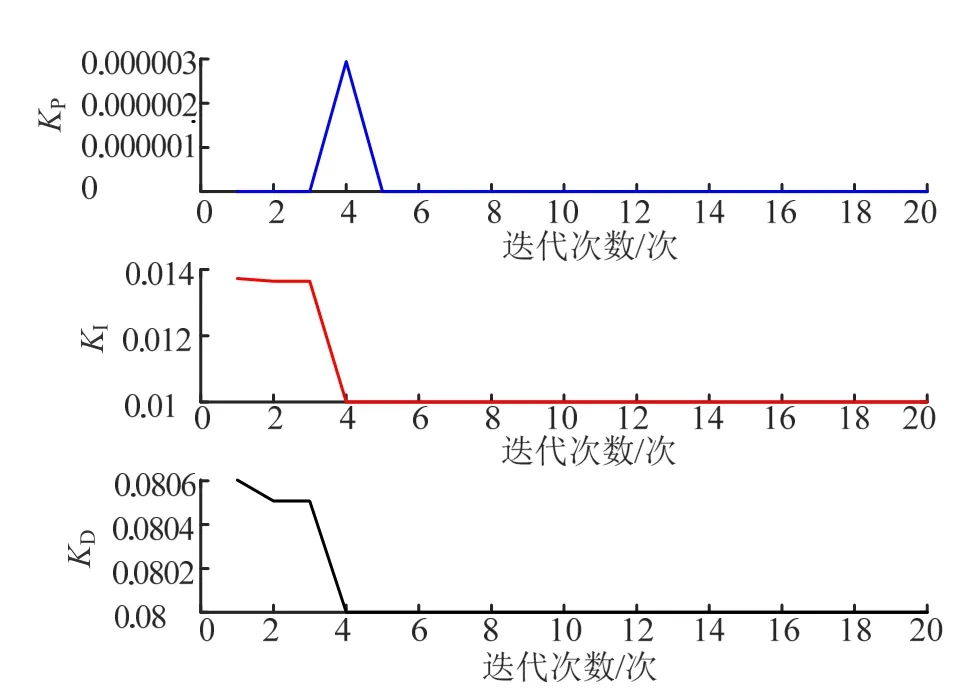
图6 kP,kI,kD 与迭代次数关系Fig.6 Relationship between kP,kI,kD Value and the Number of Iterations

图7 λ,μ 与迭代次数关系Fig.7 Relationship between λ,μ Value and the Number of Iterations
将整定好后的5 个参数带入带到惯性平台稳定回路的仿真模型中,将仿真时长设置为0.2 s,加入阶跃反应,得到如图8 所示的阶跃响应对比。
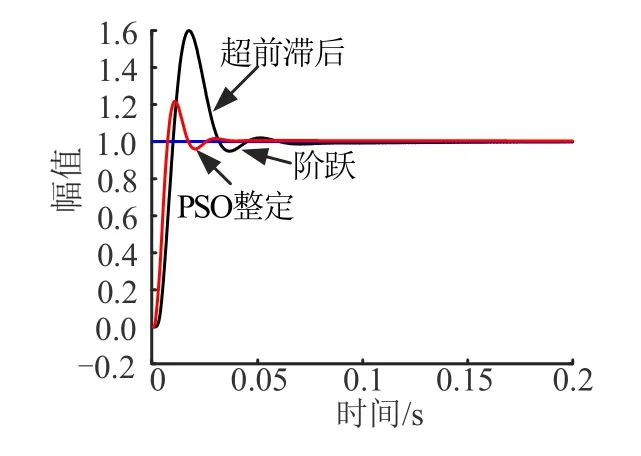
图8 阶跃响应对比Fig.8 Step Response Comparison Chart
控制力矩的数值结果如表1 所示。仿真结果表明,本文提出的方法,将最大控制力矩由原来的1.6 N·m,提高到了1.2 N·m,稳定时间从0.07 s 缩短至0.04 s,稳态误差从 8 × 10N·m 减小至 7 × 10N·m,比原来超前滞后算法提高了时域指标,仿真试验结果说明了本文提出算法的正确性和优越性。

表1 不同算法的控制性能比较Tab.1 Comparison of Control Torque with Different Algorithms
4 半实物试验验证
为验证惯性平台稳定回路实际的控制效果,搭建快速验证控制策略的半实物仿真验证环境。被控对象为稳定回路的平台系统本体,包括力矩电机、陀螺仪及对应环架。选择NI CompactRIO 平台作为半实物仿真验证平台,实现硬件控制的核心控制,用于实现陀螺仪角速度信号采集、校正网络控制计算、输出PWM等功能。由于NI CompactRIO 输出的电流为毫安级,需经过功率级电路放大后作用到平台本体的力矩电机完成整个回路的控制功能,因此设计了功率放大板,稳定回路半实物仿真验证环境的硬件实物如图9所示。

图9 稳定回路半实物仿真验证环境的硬件实物Fig.9 Hardware Physical Diagram of the Stabilizing Loop Hardware in the Loop Simulation Verification Environment
图9中,外接电源调整到28 V,用来给外接功率放大板供电;上位机将程序下载至NI CompactRIO 中进行稳定回路半实物验证;NI CompactRIO 外接功率放大板通过转接盒,连接至惯性平台用来驱动平台力矩电机。
将半实物仿真平台通过电缆连接至惯性平台上,如图10 所示,将电源柜连接市电进行供电,惯性平台和计算机柜依次上电,给陀螺仪进行加温,加温至温控点后,启动陀螺仪马达。待陀螺仪马达启动好的灯亮后,采用半实物仿真平台来实现稳定回路的功能。
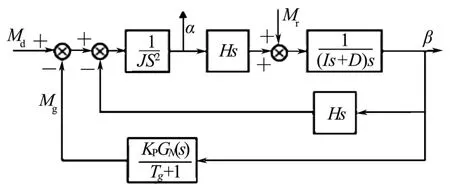
图1 惯性平台稳定回路结构Fig.1 Structure Diagram of Inertial Platform Stabilization Loop
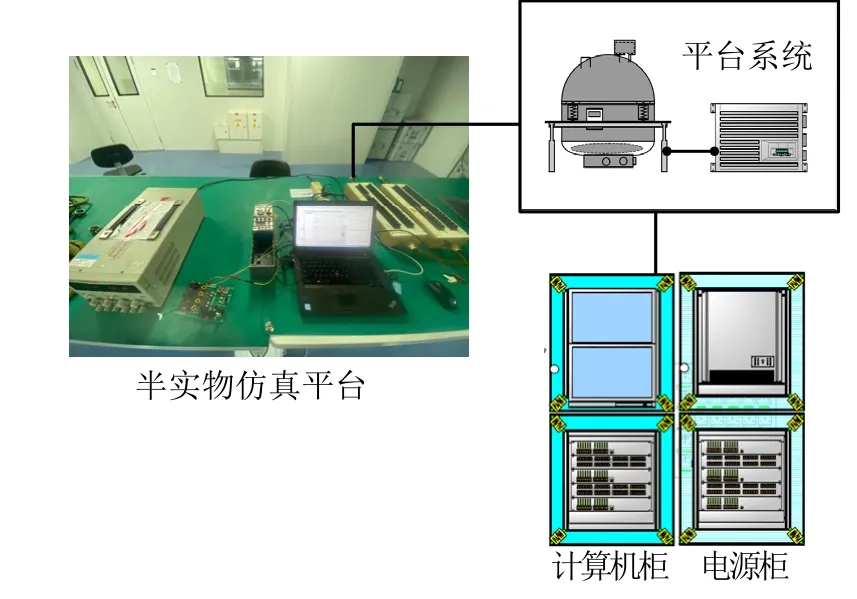
图10 惯性平台稳定回路半实物仿真验证系统Fig.10 Hardware in the Loop Simulation and Verification System of Inertial Platform Stability Hardware in the Loop Simulation Verification Environment
图11所示为分别采用传统的超前滞后方和分数阶控制器分别闭合稳定回路时的前放输出。由于系统每次启动时的初始位置随机,所以比较相应算法的稳态输出。表2 整理了两种控制器的稳定时间和稳态误差。将结果进行对比,分数阶控制器较传统超前滞后控制器相比其稳定时间从58 ms 缩短至40 ms,其稳态误差也较传统控制方法有明显的提高,为9.58222×10。由于陀螺仪输出在半实物仿真程序设计时仅采用4 次平均的方法进行滤波,所以试验中有较大的噪声,将在后续对陀螺仪输出进行滤波方法的研究。
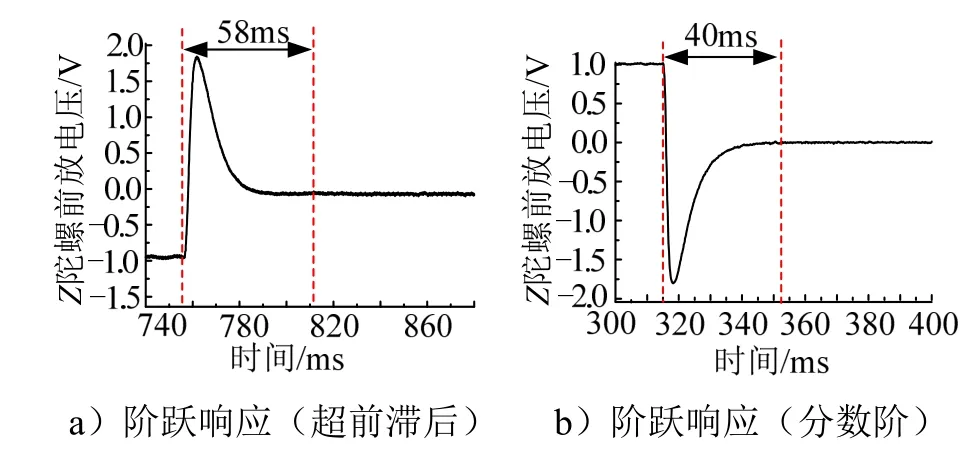
图11 半实物试验验证结果对比Fig.11 Comparison of Verification Results in Hardware in the Loop Test
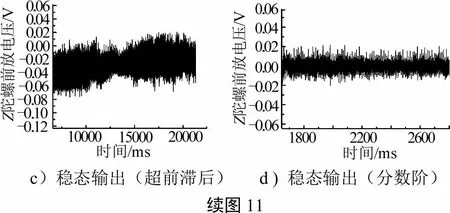

表2 不同算法闭合稳定回路Z 陀螺前放电压输出Tab.2 Different Algorithms to Close Stable Loop Z-gyro Forward Voltage Output
5 结束语
惯性平台稳定回路输入信号为陀螺信号,可以直接测得的状态变量很少,且模型存在一定的不确定性。本文采用分数阶控制器对惯性平台稳定回路进行控制,提出了一种非线性动态惯性权重自适应法改进粒子群算法的惯性平台稳定回路的分数阶控制方法,通过优化算法找寻出分数阶PID 的5 个参数,通过仿真分析及半实物试验表明,采用分数阶控制器比整数阶控制器具有更好的动态性能、更强的鲁棒性以及抗干扰能力。
