基于RBF 神经网络和SQP 算法的再入跳跃轨迹优化

杨 奔，李天任，马晓媛

（中国运载火箭技术研究院研究发展部，北京，100076）

0 引 言

跳跃式飞行器是一种在大气层内波动飞行的再入飞行器，能够通过自身携带的动力装置进行多次开关机，补充大气阻力消耗的能量，实现“向下俯冲-动力转弯-惯性爬升”的波浪式飞行。本文主要针对跳跃飞行轨迹特性进行分析，进而探讨该类飞行器轨迹的优化方法。从本质上来讲这是一种带过程约束的两点边值问题，解决该问题目前有2 种主流的算法，分别为基于非线性优化理论的直接法和基于极大值原理的间接法。1955 年，Eggers和 Seiff在简化模型下，理论推导出再入飞行器射程的解析表达式，并据此分析了平衡再入和跳跃再入轨迹的射程与气动力/气动热关系。Istratie考虑了热流密度和剩余速度，基于极大值原理研究了跳跃轨迹的优化问题。雍恩米基于高斯伪谱法对再入飞行轨迹进行了优化，验证了伪谱法具有较高的求解速度和效率。施剑锋等利用混沌粒子群法研究了跳跃飞行器在满足过程约束和航程约束的前提下实现总加热量最小的轨迹优化问题。间接法需要很强的数学理论知识，且该方法几乎无法有效解决较复杂问题；应用直接法对多阶段问题的建模较为繁琐；而粒子群法等启发式算法对于计算量大、优化参数多的复杂模型优化问题，需反复交叉、变异、迭代，计算效率较低。

20 世纪90 年代以来，由于神经网络较大的非线性拟合能力，在鲁棒飞行控制方法、气动参数在线辨识及故障诊断等方面引起了学者们广泛地研究。从原理上来讲，控制系统设计是基于模型的，因此建模是至关重要的，而对于跳跃飞行器这类非常复杂的系统，建立准确模型方法及关键参数的准确辨识问题一直无法有效解决，鉴于神经网络具有较强的映射能力优点，理论上对于对象复杂程度多高，均能快速适应。因此，成为辨识非线性系统的一种有效途径，被广泛应用于飞行器轨迹规划及控制中。

再入飞行器由于长时间在大气层内飞行，所面临的热、力等环境比较严峻，如何快速准确的实现其轨迹规划问题也显得尤为重要。本文采用RBF 神经网络对含动力的再入模型进行辨识，避免了强非线性、多阶段优化模型难以建立的困难，然后基于该辨识系统利用序列二次规划算法进行轨迹优化，在计算时间和寻优结果上均比传统方法更具优势。

1 飞行器再入轨迹优化问题

德国科学家Eugen Sänger 最早提出大气层内跳跃飞行轨迹样式，带补能装置的跳跃再入轨迹形式如图1所示。这种轨迹最显著的特点是飞行高度起伏变化大且不具规律性，相比于传统的抛物形、平衡再入式轨迹，其特征参数更加不易获取。除此之外，由于长时间在高空飞行，可以减少速度损失和降低热载，具备一定的工程应用价值。

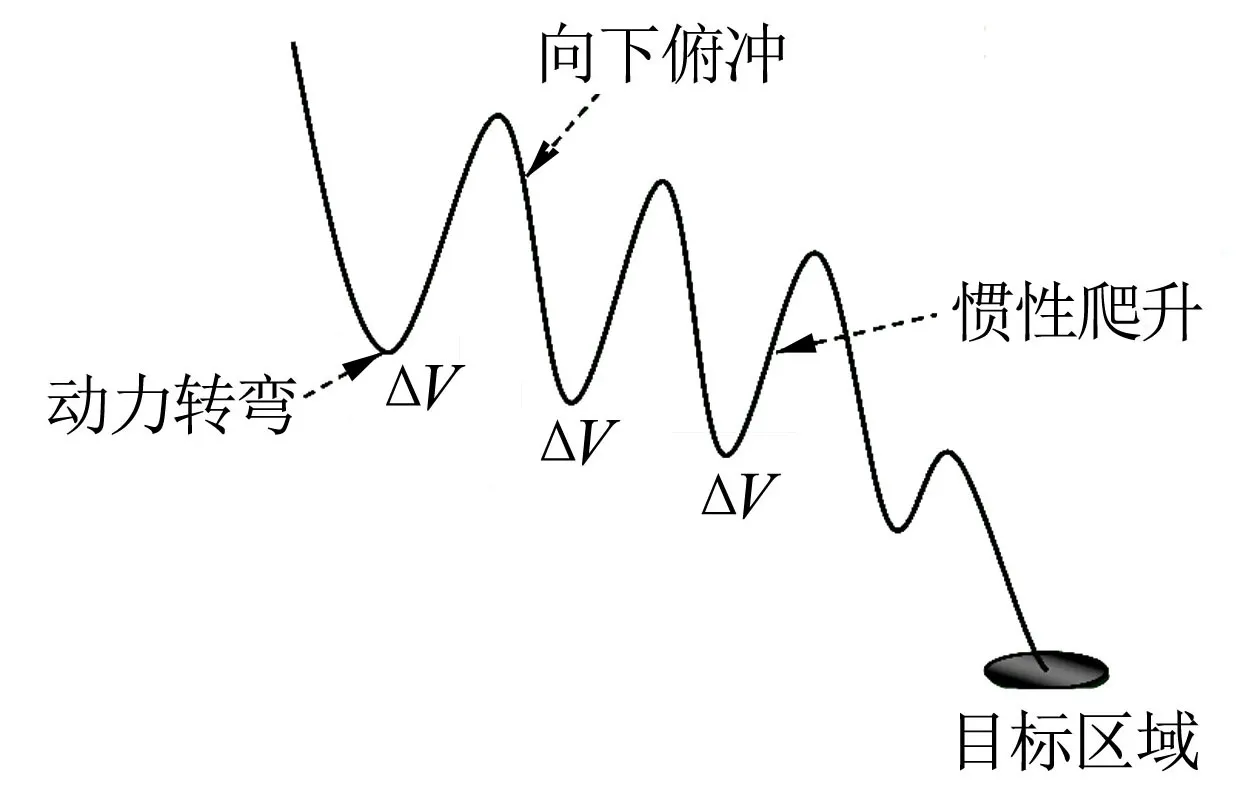
图1 跳跃轨迹示意Fig.1 Schematic Diagram of Skip Trajectory

1.1 再入动力学模型

为简化问题，只研究再入飞行器纵向平面内的运动，假定地球为一静止的圆球，带动力的再入飞行器无量纲动力学模型为

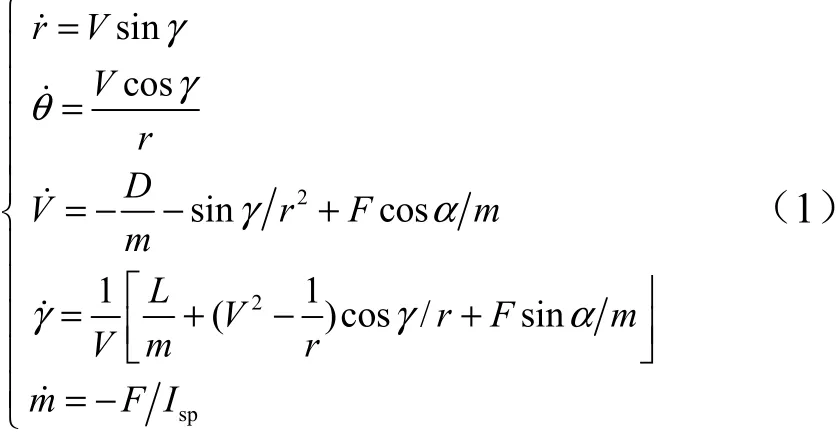
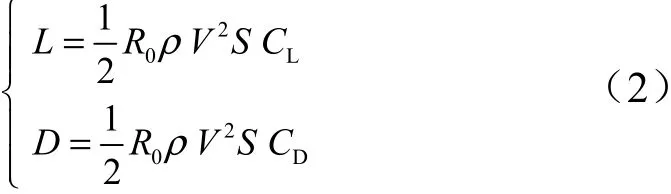
式中为大气密度；为飞行器质量，=907 kg；为参考面积，=0.4839 m；为升力系数；为阻力系数，均参考国外滑翔飞行器CAV-H。对升力系数和阻力系数进行拟合，得到两者对攻角的关系式：

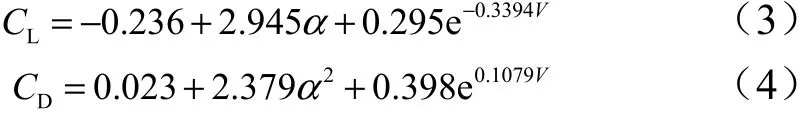
1.2 优化问题描述

再入跳跃轨迹优化问题一般可以转化为包含路径约束、边值约束以及补能发动机工作时间约束的优化问题。本文主要研究不同飞行策略对末级发动机开关机时间点的影响，暂不考虑攻角对结果的影响，因此借鉴航天飞机的程序攻角设计方法，采用典型的二次分段标称攻角剖面，其具体表达形式为

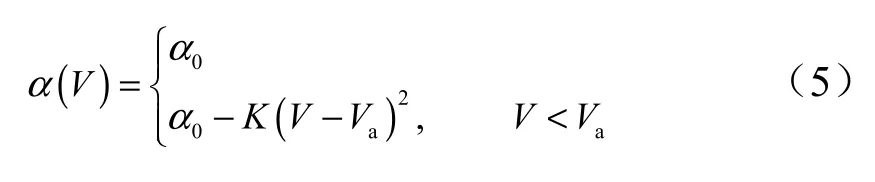
式中为再入初始攻角，在再入段的初始阶段，以大攻角飞行，避免飞行器超过热流的约束；为飞行攻角设置的速度阈值；为常量系数。

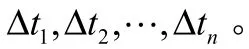
再入轨迹优化问题一般是考虑射程最远为优化指标，但防热问题也是再入飞行器在大气层内飞行时需要考虑的一个重要方面。本文将两者综合考虑，将热流约束通过罚函数策略加入到性能指标中，因此选择两者的加权作为设计的优化指标，并讨论不同飞行策略下的开关机方案，即：

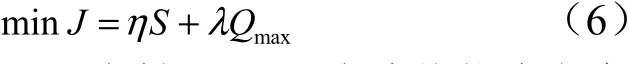
式中为性能指标；为射程；为峰值热流密度；，分别为射程和峰值热流的权值系数。

2 基于RBF 神经网络的再入跳跃系统辨识

针对该多阶段优化模型，文献[5]中基于混沌粒子群法进行计算，但该方法中选择、变异、混沌化以及轨迹积分等操作过程需要大量迭代运算，计算量大，且实际求解过程中的计算精度难以保证，难以满足实时性要求。

因此，本小节将引入RBF 神经网络，利用其强大的非线性映射能力，构建以末级发动机3 次波谷的工作时间和适应度值的映射关系，完成基于RBF 神经网络的再入跳跃系统辨识。

2.1 RBF 神经网络的原理

RBF 网络是一种包含输入层、隐含层和输出层的前馈神经网络，输入端到输出端的映射关系是非线性的，但中间层到输出端的映射是线性的，该网络一般结构如图2 所示。

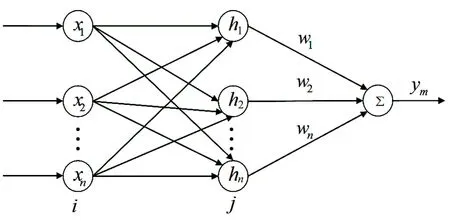
图2 RBF 神经网络拓扑结构Fig.2 RBF Neural Network Topology

图2中：a）输入层：由感知单元组成，主要是用来感知外部环境变化。b）隐含层：也可称为激励函数，是网络对输入条件产生局部调节。c）输出层：该层的节点对隐含层的输出数据进行线性处理，从而形成输入端到输出端的映射空间。因其网络结构简单、训练简洁、学习收敛速度快，适合实时控制的要求。

本文中，为避免直接求解非线性、多阶段的优化问题的困难，将末级发动机3 次的工作时间作为输入，射程、热流以及两者的加权函数等不同飞行策略指标作为输出，利用RBF 网络实现对发动机每次波谷工作时间与适应值函数非线性系统的辨识。

2.2 RBF 神经网络的训练

在网络结构中，= [,, …, x]为网络的输入向量。设基向量= [,,… , h]，其中,为底函数，即：

式中 第个节点的中心向量为

设基宽向量为= [,,… , b]，为节点的基宽参数，且为大于零的数。网络的权向量为

则，RBF 网络的输出为

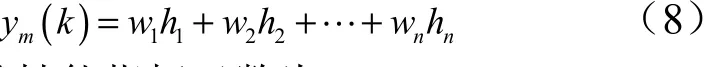
网络逼近的性能指标函数为

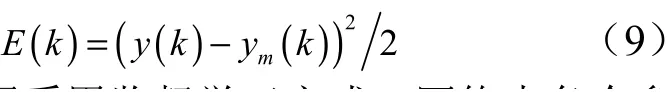
网络学习过程采用监督学习方式，网络中各个参数的迭代算法如下：

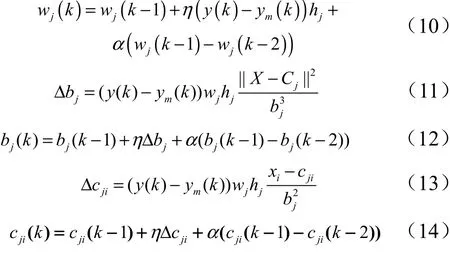
式中为学习速率，∈[0 ,1 ]；为动量因子，∈[0 ,1 ]。

2.3 序列二次规划算法

序列二次规划算法的原理是在参考点处，降阶求解二次规划的子问题，通过寻优结果更新参考点，使其逐步逼近原优化问题的最优解。由于该算法具有全局最优性的同时保持部分超1 次收敛性能，成为目前求解非线性规划问题最受欢迎的算法之一。

设,,分别表示性能指标、等式与不等式约束，考虑如下最优控制问题（P）：

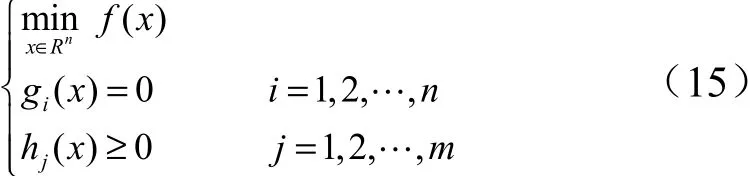
在 x处，与式（15）对应的二次规划子问题（QP）表示为

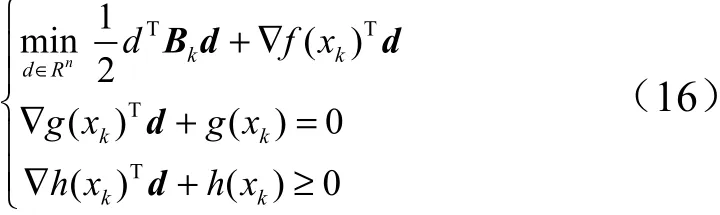
式中 ∇(x)，∇(x)，∇(x)分别为函数,,在 x处的梯度；矩阵B为问题（P）的 Lagrange 函数(,,) =() +() −()在Hessian 矩阵的拟牛顿近似矩阵；为搜索方向。为使算法具有收敛性，通常要求B对称正定。对于式（16）的二次规划问题，一般可采取罚函数等方法进行快速优化。

2.4 训练样本的产生和算法流程

假设再入飞行器携带燃料一定，并规定燃料在前3 次波谷阶段完全燃烧。在此基础上，随机生成组Δ、Δ和Δ数据，分别为每次波谷发动机的工作时间。正如第1.2 节所分析的，选择发动机开机时刻为波谷点，体现在时间-地心距曲线上即曲线的凹点，其表示为

式（17）中所表示的是连续系统的波谷点，但实际仿真过程是一系列的离散点，所以必须对式（17）进行处理，从而得到式（18）表示的开机点时刻。

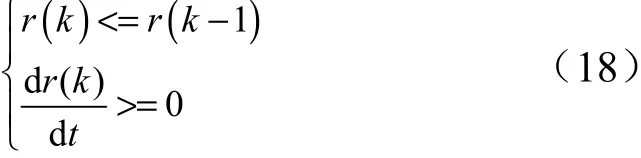
随后，从再入飞行器的初始状态通过龙格库塔四阶积分，直到飞行器达到末端高度约束，计算每组数据所对应的适应值，从而形成大量的样本用于RBF 网络训练。

基于上述辨识系统，利用序列二次规划算法对其进行轨迹优化。

3 数值仿真及分析

为验证本文方法的准确性和有效性，选取美国通用飞行器的再入任务进行仿真分析，该飞行器总质量为907 kg，参考面积为0.48 m。标称攻角剖面为：0=22°，=16，=0.11。飞行器的初始飞行状态如表1 所示。飞行器所携带燃料为16 kg，末级发动机推力为2000 N，比冲为=49 000 m/s。

表1 飞行器再入点参数Tab.1 Reentry Point Parameters

3.1 RBF 网络辨识结果分析

按照第2.2 节中数据产生的方式，生成10 000 组发动机各个波谷点工作时间组合以及对应的适应值数据，作为监督学习的数据库。网络输入层感知单元为3 个，输出神经元的数量为1，考虑网络的映射能力和学习效率，隐含层节点数量为112。

在网络训练过程中，随着逐步迭代，其输出与样本真值之间的差值逐渐减小，最终收敛至稳定，误差最终收敛于 1 × 1 0，表明网络达到了较高的收敛精度。

为验证所建立的RBF 神经网络对原非线性、多阶段系统的逼近程度，随机生成100 组Δ、Δ和Δ数据，输入到RBF 网络模型中，并同时将其带入到式（1）中进行飞行参数计算，将两者所得的结果比较，作为网格辨识精度的评价标准，进行误差分析。在随机生成100 组输入量的状态下，所训练的网格成功得到了输入量对应的的适应值。与真实值相比，最大误差2.5 × 10。说明该网格可以实现对原有系统的准确辨识，准确地建立了3 次波谷发动机工作时间和与适应度函数的非线性映射模型。

3.2 序列二次规划算法对辨识系统的轨迹优化

基于第3.1 节中RBF 神经网络对原复杂系统的逼近模型，采用序列二次规划算法进行轨迹优化。下例中，规定式（6）中=1，=70 综合考虑射程最优和热流约束。通过给定不同的初始参考点，对比分析其优化结果（见表2），说明该模型对初始值的依赖较低，可以很好地避免对原系统直接优化不易建模的困难。

表2 轨迹优化结果对比Tab.2 Result Contrast

由表2 可知，3 组不同的初始方案，得到的优化结果一致，说明基于RBF 神经网络和SQP 算法跳跃轨迹优化方法对初值敏感度低，并且在较少的迭代次数后达到收敛，迭代结果如图3 所示，3 种情况耗时均在0.275 s 左右。

图3 不同初始轨迹的优化结果Fig.3 Optimization Results of Different Initial Trajectories

图3是不同初始参考值所对应的优化结果，由于本次仿真所选取的性能指标是综合考虑了射程最优和热流约束，所以优化结果是第2 次波谷时刻发动机工作时间最长，其次是第1 次波谷时刻，第3 次发动机并未开机，在此之前燃料已经消耗完毕。在第3.4 节里，会对不同飞行策略的轨迹特性进行分析对比，并说明其对每次波谷发动机工作时间的影响。

由图3 可知，末级发动机分别在108.4 s 和361 s时刻开始点火，并分别持续工作17.62 s 和22.38 s。在前2 次波谷附近内，速度有短暂的增加，轨迹倾角和高度变化并没有发生突变，过渡比较平稳，说明该优化方案是可行的。

3.3 与混沌粒子群法寻优结果对比

粒子群算法对性能指标和约束条件的限制较少，具有较强的全局寻优能力，优化模型简单、通用性强，但对于较为复杂的问题，受其交叉、迭代等步骤的影响，粒子群法的优化效率较低，优化时间一般在几十分钟甚至小时量级。在传统粒子群算法中，初始化是随机设置的，可能导致某些可行域被遗漏，无法保证种群空间的随机性与多样性，很难求得最优解。将混沌算法与粒子群算法相结合，将其应用于优化搜索中，利用混沌运动的随机性、充分调整种群的进化方向，最大程度上避免陷入局部最优解。

为验证本文算法的准确性和高效性，将优化结果与混沌粒子群算法的寻优结果进行对比，粒子群算法主要参数设置为：学习率==1.4，最大迭代次数为=45，粒子空间为3 维，种群数量维为100。具体的对比结果见表3 和图4。

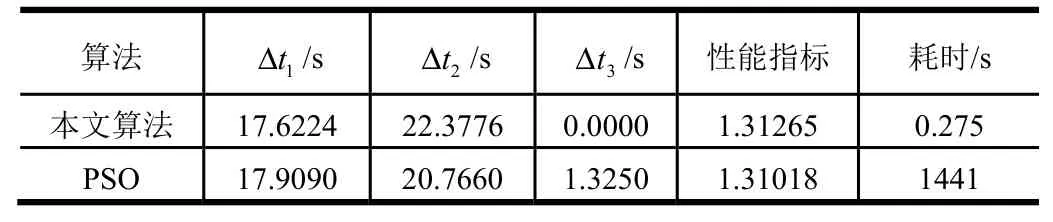
表3 寻优结果对比Tab.3 Comparison of Optimization Results

图4 两种算法优化的射程-高度曲线Fig.4 Range-height Curve Optimized by Two Algorithms

由表3 和图4 知，采用基于混沌粒子群法的寻优过程在经过44 次反复迭代寻优、交叉变异步骤后，计算结果与本文算法基本一致，总计耗时1441 s 左右，时效性不高，寻优结果与本文算法计算结果相比，无论是从计算效率还是结果的最优性方面，基于RBF 神经网络和SQP 算法的跳跃轨迹优化结果都表现出绝对的优势。

3.4 不同飞行策略的轨迹特性对比

为了分析不同的飞行策略对末级发动机各波谷工作时间的影响，本小节通过设置不同的适应值函数以及对应的优化指标，分别采用RBF 神经网络对原多阶段系统进行逼近，随后利用序列二次规划算法对其进行轨迹优化，具体方法同第3.1 节和第3.2 节。

分别采用如射程最远、最大热流密度最小化等不同的飞行策略，研究其对末级发动机各波谷工作时间的影响。仿真结果见表4、图5、图6 等。

表4 不同飞行策略的结果对比Tab.4 Comparison of Results under Different Flight Strategies

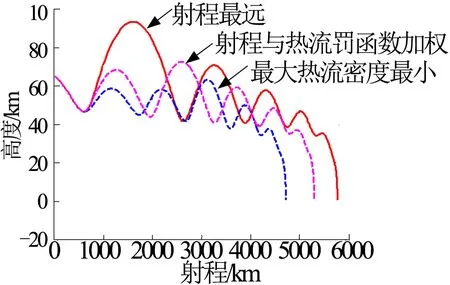
图5 不同飞行策略对应的射程-高度曲线Fig.5 Range-altitude Curve Corresponding to Different Flight Strategies

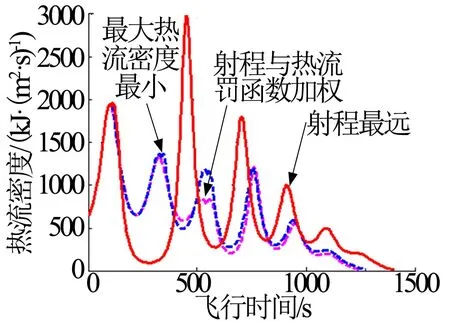
图6 不同飞行策略对应的热流密度曲线Fig.6 Heat Flux Curves Corresponding to Different Flight Strategies

由图6 可知，在只考虑热流密度约束时，所优化的结果是，发动机工作时间比较靠后，反而第1 次发动机工作时间只有1.0432 s，这也与第1种情况相对应。因此可以得到，发动机工作时间越靠前，射程越远，但热环境压力大。发动机工作时间越靠后，能减轻热环境压力，但却严重减小了飞行器的射程。在这种情况下，本文综合考虑射程与热环境条件，以射程与热流罚函数加权为优化指标，达到兼顾两者的效果。

4 结束语

本文通过采用RBF 神经网络对原强非线性、多阶段的再入跳跃式轨迹模型进行辨识，借助神经网络强大的非线性映射能力，建立了末级发动机3 次开机点时间和与适应度函数的非线性映射模型。在此基础上，采用序列二次规划算法进行轨迹优化，避免了直接求解该优化问题的困难。并与基于混沌粒子群算法的寻优结果进行对比，验证了该方法的准确性和高效性。

另外，讨论了射程最大、热流最小等不同的飞行策略对开关机时间的影响，并从实际工程角度出发，为兼顾不同的性能指标，提出以射程和热流罚函数加权为优化指标，并通过对大升组比再入飞行器CAV-H进行仿真分析，得到了较优的轨迹，具有一定的工程应用价值。