基于三维模型空间离散的固体发动机装药燃面计算方法

费 阳，解红雨，张治宇，冯 翔

（中国人民解放军96901 部队，北京，100094）

0 引 言

装药燃面计算是固体火箭发动机内弹道性能预示的重要内容，其计算精度直接影响发动机优化设计效果和性能预示精度。传统的药柱燃面计算方法包括作图法、解析公式法和通用坐标法；对于三维复杂药型，可用CAD 实体造型法和数值算法等。CAD 实体造型法目前在发动机工业设计部门使用较普遍，需要对UG、SolidWorks 和ProE 等商业软件进行二次开发，燃面设计时，需要专业人员干预操作；有学者利用最小符号距离算法和惠更斯原理，实现了复杂三维药柱燃面计算，但是该方法在非并行计算条件下计算效率较低。基于体素离散化的药柱燃面计算方法，利用MC 界面重构算法实现了复杂构型装药燃面计算，但MC 算法的体素表存在二义性问题，在计算网格稍粗的情况下可能影响计算精度。Level-set 界面追踪法通用性较强，但是该方法初始燃面定义十分复杂，需要手动进行代码定义，因此药型定义精度受限；另外，该算法追踪燃面时，需要燃面附近多层“窄带”网格点信息的迭代计算（重新初始化计算），此特性不仅降低计算效率，还导致燃面过早下降。

针对现有燃面计算方法的缺陷，本文利用SolidWorks 商业软件对三维复杂构型药柱芯模进行建模，将芯模表面（初始燃面）生成STL 数据文件，将初始燃面三维笛卡尔坐标系中进行离散描述，通过空间距离场算法计算空间离散点到初始燃面的最小符号距离，然后利用空间离散点最小符号距离信息快速计算燃面。此方法充分利用已有实体建模软件，初始燃面定义快捷精确，燃面计算过程中无需迭代计算；针对最小符号距离计算量较大的问题，可将三维笛卡尔离散空间划分成多个计算区域，进行多线程并行计算，极大提高计算效率。

1 燃面计算方法

1.1 总体思路

本文燃面计算方法总体思路如图1 所示。

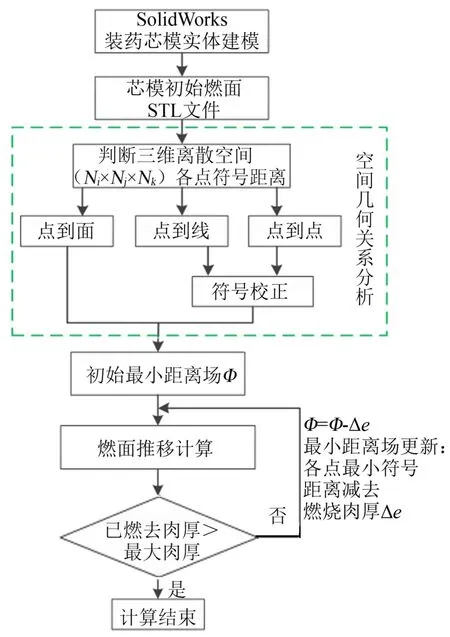
图1 燃面计算总体思路Fig.1 The Outline for Burning Surface Calculation

首先利用SolidWorks或ProE等商业软件对推进剂药柱芯模进行实体造型，然后将芯模实体构成初始燃面的表面生成STL 文件。构造一个恰好能包络药柱、以{,,}为单位正交基底的三维笛卡尔空间区域，将空间区域在、、方向上离散成N ×N ×N个空间点，将方向设置为药柱轴向，且空间坐标轴原点与STL 文件坐标轴原点重合。通过空间几何关系分析，得到各空间点到初始燃面的最小符号距离Φ , 。然后，利用面积积分算法对燃面进行计算。假设燃烧肉厚为Δ，将各空间点最小符号距离Φ, 进行更新Φ , ,Φ , Δ，重复上述步骤，即可得到不同燃烧肉厚的燃面。

1.2 装药芯模初始燃面STL 文件

STL 文件格式用三角面片表达实体表面数据信息。ASCII 码STL 文件格式如表1 所示，ASCII 码格式STL 文件逐行给出三角面片的几何信息，每行以1个或2 个关键字开头。在STL 文件中，由多个三角形面片facet 信息构成，每1 个facet 由7 行数据组成，第1 行facet normal 为三角形面片的单位法向量，在本文中，单位法向量由燃面指向药柱内部。第3 至第5行为三角形的3 个顶点坐标，且单位法向量方向与3个顶点的依次顺序遵循右手法则关系。

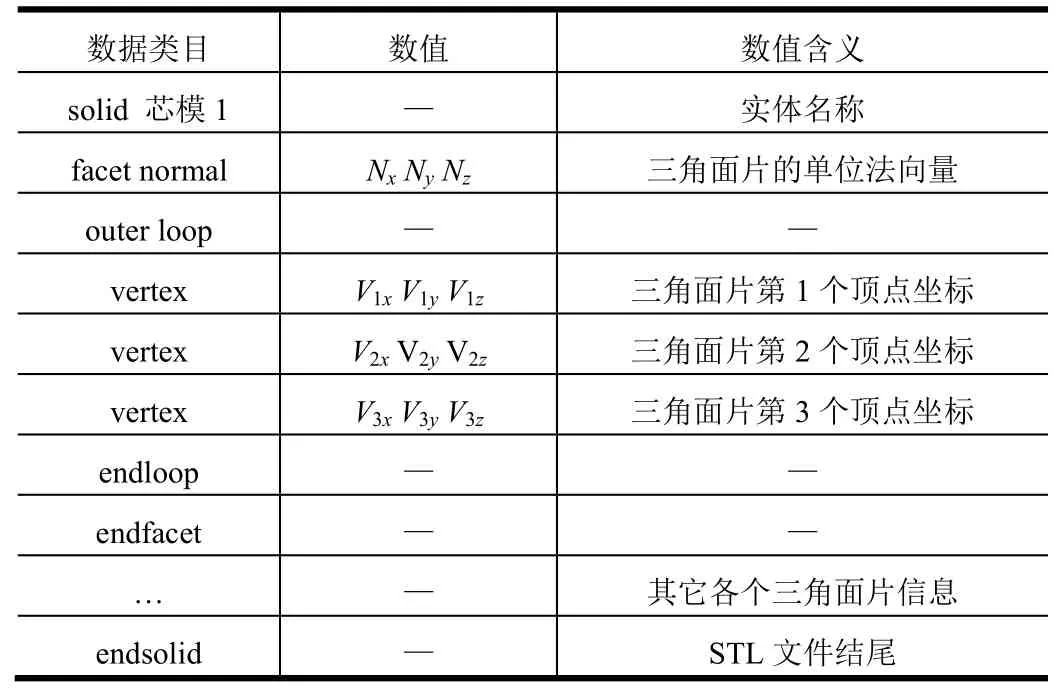
表1 初始燃面STL 文件格式Tab.1 The Data Format of the Initial Burning Surface STL File

1.3 空间最小符号距离计算

最小符号距离场是指在以{,,}为单位正交基底的空间直角坐标系中，三维笛卡尔离散空间中（N ×N ×N），每一个空间离散点到燃面的最小符号距离Φ, ，Φ, ,> 0表示当前空间点处于药柱内部，Φ , ,=0表示当前空间点恰好位于药柱燃烧表面，Φ, ,< 0表示当前空间点位于燃烧室空腔。因此，除了计算最小距离之外，最小距离符号的判断十分重要。利用STL 文件准确计算初始最小距离场是实现燃面计算的关键。

燃面计算总体思路如图2 所示。

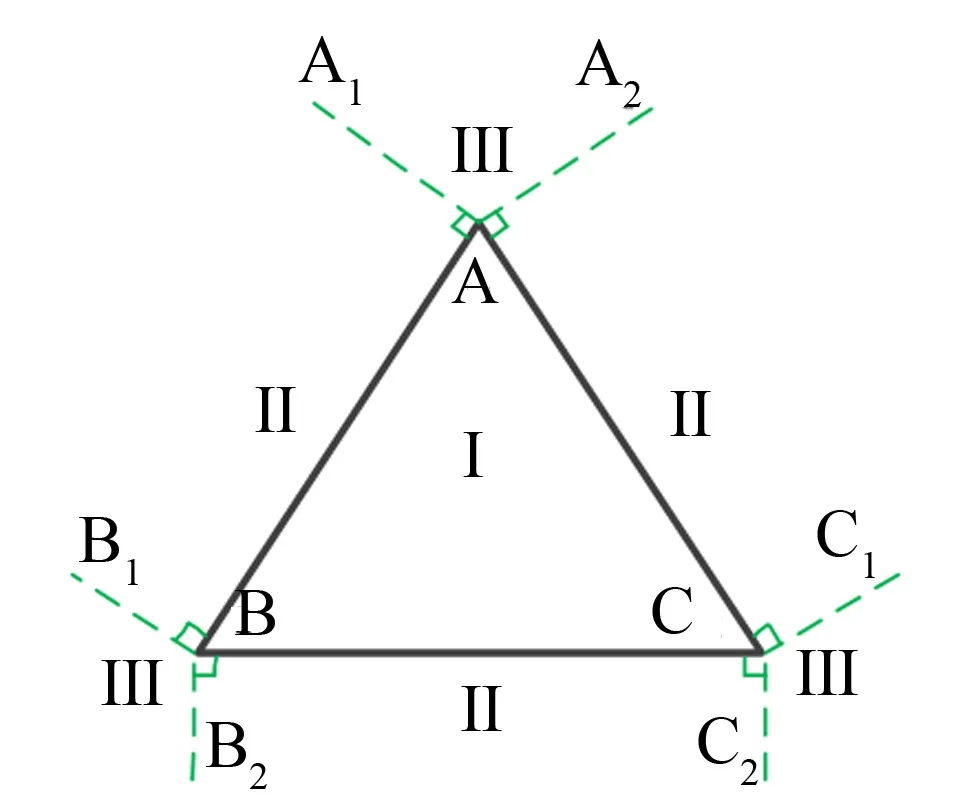
图2 燃面计算总体思路Fig.2 The Outline for Burning Surface Calculation

如图2 所示，以三角形面片 ΔABC为例，设为其单位法向量，、为垂直于AB 边并指向三角形外部的单位向量，、为垂直于BC 边并指向三角形外部的单位向量，、为垂直于AC 边并指向三角形外部的单位向量。这些有向线段和三角形面片将平面区域划分成7 块、共3 种情况的子区域。假设空间点为，讨论不同情况最小符号距离计算方法。

1.3.1 点到面

如图2 所示，若空间点P 点需满足式（1），P 到Δ ABC 所在平面的投影在区域I（ ΔABC内部），空间点P 到 ΔABC的最小距离就是P 到 ΔABC的垂直距离，可由式（2）计算，最小距离的符号可由式（2）直接确定。

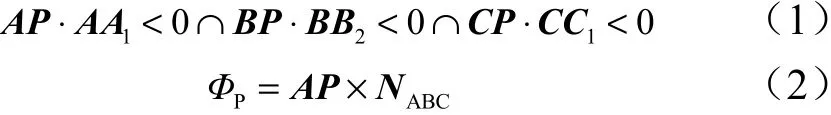
1.3.2 点到点

如图2 所示，当空间点P 到 ΔABC所在平面的投影在区域III 时，空间点P 到 ΔABC的最小距离就是P 到Δ ABC 顶点的直线距离。若点P 需满足式（3），则P点到顶点A 距离最近；若点P 需满足式（4），则点P到顶点B 距离最近；若点P 需满足式（5），则点P 到顶点B 距离最近。

多个三角形共点的情况下符号判断见图3。

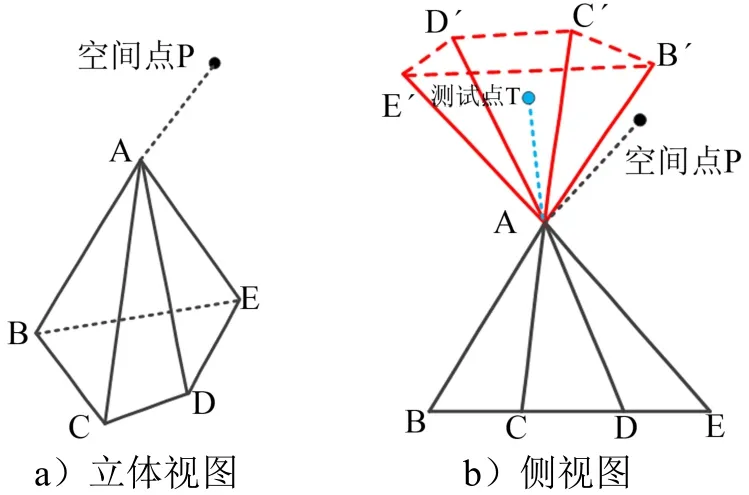
图3 多个三角形共点的情况下符号判断Fig.3 Sign Identification when the Adjacent Triangles Share One Point

如图3a 所示，当顶点A 被多个三角形面片公用时，由式（2）确定的符号可能随三角形的不同而变化，因此，需要构造测试点T，T 到所有三角形的最小符号距离符号相同。如图3b 所示，以A 点为起点，沿着、、、分别构造单位向量′、′、′、′，测试点T 在坐标系中的位置可由式（6）确定，然后利用式（7）确定符号。

1.3.3 点到边

如图2 所示，当空间点P 到 ΔABC所在平面的投影在区域II 时，空间点P 到 ΔABC的最小距离为P 到Δ ABC 某条边的垂直距离。若点P 需满足式（8），则点P 到边AB 距离最近；若点P 需满足式（9），则点P 到边BC 距离最近；若点P 需满足式（10），则点P 到边AC 距离最近。

三角形共边情况下符号判断见图4。以点到BC边的最小距离为例，如图4a 所示，当BC 边被2 个三角形（ ΔABC、 ΔBCD）共享，且两三角形平面夹角小于90°时（图4b），若点P 处于1、3 区域，由 ΔABC、Δ BCD 判断点P 的符号不一致。如图4c 所示，在 ΔABC和 ΔBCD的夹角平分面上构造测试点T，T 到 ΔABC、Δ BCD 有相同的距离符号。利用式（11）、式（12）在面ABC、面BCD 上构造单位向量、，且、垂直于BC。记BC 中点为M，测试点T 坐标可由式（13）确定，然后利用式（14）确定符号。

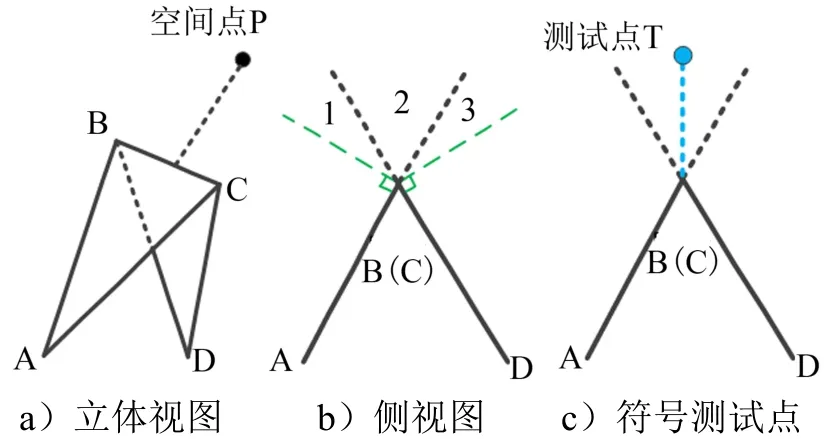
图4 三角形共边情况下符号判断Fig.4 Sign Determination when the Adjacent Triangles Share One Edge

1.4 燃面积分

获得计算空间内各离散点的最小符号距离后，就可利用各种面积计算方法求得燃面。将包覆层等阻燃物质转化为数学描述的积分限，记燃烧室内部区域为。对于复杂三维装药，直接引入面积计算公式（15），该计算公式被Level-set 计算程序广泛采用，仅需要燃面附近1~2 层离散点信息：

式中为时刻燃面面积；下标为计算区域中任意一点(,,) ；() 为当地最小距离函数。式（15）中函数定义为

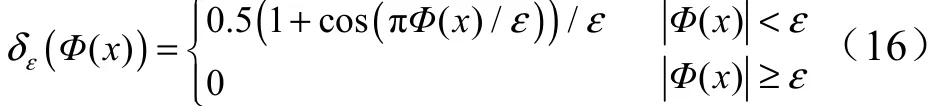
式中= 1.5min( Δ,Δ, Δ)。

2 算例分析

利用燃面计算方法对星孔型二维药柱和翼柱型三维药柱进行燃面计算，将计算结果与CAD 实体造型法进行对比，验证计算方法的正确性和准确性。计算所用工作站CPU（Xeon E3-1230）核心数为16，核心主频为3.5 GHz。

具体过程为：对算例药柱内部空腔（即药柱芯模）进行SolidWorks 实体建模，选取所有空腔表面（即药柱初始燃面），以装药尾部端面中心为三维笛卡尔坐标原点，轴和轴所在平面垂直于药柱轴向，轴为装药轴向由尾部指向头部，输出STL 文件（文件格式如表1 所示），燃面计算模块读取STL 文件，在相同坐标系下，根据药柱外径、长度信息自动构建恰好能包裹装药的长方体计算空间，根据芯模最小特征尺度（如翼宽、星尖半径等）合理设置计算网格尺度Δ、Δ、Δ，然后进行1.3 节所述的燃面计算过程。

2.1 星孔型二维药柱

星孔型装药结构如图5 所示。

图5 星孔型装药结构示意Fig.5 A Structure Representation of A Star-shaped Propellant Grain

算例1 采用图5 所示星孔型装药，两端及外侧包覆，内表面燃烧。星孔型装药燃面计算虽有精确的解析公式，但解析公式无法计算燃面达到包覆层后面积迅速下降的过程，为全面检验本文方法准确性，本算例与CAD 实体造型法进行对比。实体造型法被工业部门广泛应用，精度较高。初始燃面最小符号距离计算过程中，药柱芯模STL 文件三角面片数量为1158，计算网格数量为300×300×500，将包覆层转化为积分上限，若燃面超出包覆层，则不对其积分。计算采用32个并行线程数，计算时间为25.325 s。图6 为星孔型装药燃面计算结果对比曲线，二者吻合较好，平均相对误差为1.25%，最大相对误差为3.36%。燃去肉厚达50 mm 时，燃面抵达侧面包覆层，燃面迅速下降。

图6 星孔型装药燃面计算结果对比Fig.6 A Comparison of the Burning Surface Results between this Method and Cad Modeling Method

2.2 翼柱型三维药柱

为进一步考察燃面计算方法的通用性、准确性，算例2 采用图7 所示翼柱型装药，两端及外侧包覆，内表面燃烧。利用本文方法对其平行层推移过程进行仿真。三维翼柱型装药燃面没有解析公式，本算例与CAD 实体造型法计算结果进行对比。初始燃面最小符号距离计算过程中，药柱芯模STL 文件三角面片数量为3152，计算网格数量为350×350×1000。同样，程序中将包覆层转化为积分限，若燃面超出包覆层，则不对其积分。计算采用32 个并行线程数，计算时间为127.559 s。

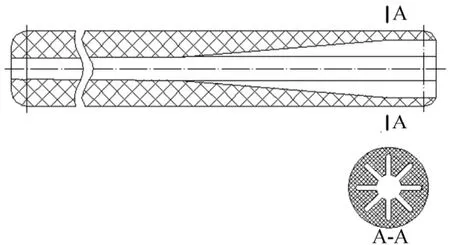
图7 翼柱型装药结构示意Fig.7 A Simplified Structure of A Back-wing Propellant Grain

图8为翼柱型装药燃面计算结果对比。

图8 翼柱型装药燃面计算结果对比Fig.8 A Comparison of the Burning Surface Results between this Method and Cad Modeling Method

二者吻合较好，平均相对误差为1.33%，最大相对误差为3.07%。图中A-A 截面为后翼剖视图。

3 结束语

本文对固体发动机药柱芯模进行CAD 实体建模并生成STL 文件，利用最小符号距离算法，将STL 文件生成初始燃面空间最小符号距离场，通过最小符号距离场信息实现复杂三维药柱燃面计算。计算结果与CAD 实体造型相比，吻合较好。利用多线程并行计算技术，极大提高了计算效率。该方法无需通过代码定义药柱构型和迭代计算，可直接用于不同固体发动机药柱设计。