浅析数形结合思想在小学数学教学中的应用

付红波

摘 要：数形结合既是一种重要的数学思想，又是一种常用的数学方法，在小学数学教学中广泛应用，本文介绍相关概念并结合人教版小学数学教材，初步整理了数形结合思想方法在各教学领域的渗透与应用。

关键词：小学数学;数形结合

数形结合思想是小学数学中的一种重要思想。它是在数与形之间的本质联系上，以“形”直观的表达数，以“数”精确的研究形的思想方法。在數形优势互补的基础上，把抽象的数量关系与直观的图形结构结合起来，使数量的精确刻画与空间形式的直观形象巧妙、和谐的结合在一起。充分利用这种结合，寻找解题思路的一种思想。利用数形结合思想可以解决许多数学问题。数学家华罗庚说：“数缺形时少直观，形少数时难入微，数形结合百般好，隔离分家万事休”。利用树形结合能使“数”和“形”结合起来。以形助数、以数辅形，可以使许多数学问题变得简单化。那么如何在教学中有效渗透数形结合的思想，下面就结合我的教学实践谈一些粗浅的认识。

一、以形助数，化抽象为直观

1.刻画概念本质

例如：在教学《义务教育教科书》（人教版）三年级数学上册《倍的认识》这一课时。可以利用图形直观的呈现两个量之间的倍数关系，让学生在两组图形的观察比较中由“几个几”转化为“倍”，借助几何直观把复杂的数学问题变得简明、形象，使学生对“倍”的认识由浅入深，对“倍”的感性认识上升到理性认识，最终建立“倍”的概念。

再比如四年级下册《小数的意义》的学习中，小数是一个十分抽象的概念，它与分数相比更加抽象。我们同样是通过数与形的结合，帮助学生理解掌握小数的意义、小数的大小、小数的性质。通过1米=10分米，让学生理解1分米=0.1米，并类推出1厘米=0.01米，1毫米=0.001米;通过数与形完美的结合——数轴，让学生理解小数的组成、小数大小的比较、小数与整数的关系等。总之，这种数形结合直观的帮助学生进行对比、理解，使学生在自我思维里清晰的刻画了概念的本质。

2.明晰数量关系

数形结合不仅是一种数学思想，也是一种很好的学习方法。把数量关系和空间形式结合起来去分析问题、解决问题，这就是数与形结合思想。教学中引导学生应用数形结合的思想可以把复杂问题简单化，把抽象思维具体化，把数量具体化、清晰化、量与量之间的关系就更清晰。

例如：画图解决分数应用题

新人教版数学六年级上册第16页练习三

第5题：鸡的孵化期是21天，鸭的孵化期比鸡长。鸭的孵化期是多少天？

要解决这个问题，需要理解鸡和鸭孵化期的数量关系，但单凭文字，数量关系就比较抽象，这个时候借助画图可以化繁为简、变抽象为直观，明晰了两个量之间的数量关系。

如图：

鸡的孵化期：

鸭的孵化期：

从图上直观的看出鸭的孵化期是鸡的，解决鸡的是多少就是鸭的孵化期。通过这样的画图分析，使学生明了了两个量之间的关系，并轻松的解决了这样难以理解的问题。以后学生可以利用这样的方法，分析问题并解决问题。

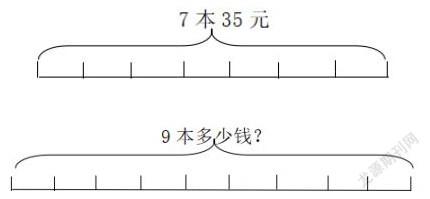
又如：新人教版数学三年级上册有关倍的内容

小强买7本笔记本，用去了35元。买9本同样的笔记本，一共需要多少钱？

解决买9本需要多少钱，对于逻辑思维差的学生来说，是难以解决的。这个时候借助画图，能让学生清晰的看出把35元平均分成7份，每份就是一本的价格，根据一本的价格从而解决9本多少钱这个问题。

从图中可以看出7本一共35元，1本就是5元，那么求9本多少钱，其实就是就9个5是多少。通过画图，使学生直观的看出要先解决单价，才能明晰求9本多少钱其实就是求9个5也就是5的9倍是多少。

3.直击问题本质

数形结合能把抽象性问题清晰化，便于观察，并直击问题的根源和本质，运用数形结合的思想来解决问题，揭示问题的本质，可促进学生形象思维和抽象思维的协调发展，更能促进学生的可持续发展。

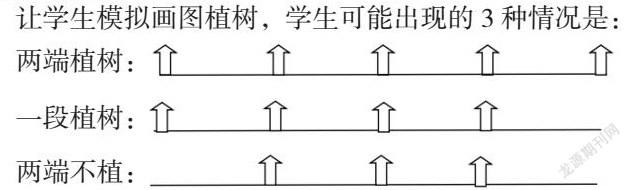
例如：“植树问题”。在一条20米的小路上植树，每隔5米植一棵，可以植多少棵？

让学生模拟画图植树，学生可能出现的3种情况是：

两端植树：

一段植树：

两端不植：

学生通过图形的观察建立了棵数和段数之间的联系，并通过理解探索出棵数和段数之间的联系——归根结底就是一一对应的关系，既棵数和段数一一对应。两端植树就是棵数和段数一一对应后，还剩一棵树，棵数=段数+1。只植一端就是棵数和段数刚好一一对应，棵数=段数。两端都不植段数和棵数一一对应后，段数比棵数多1，棵数=段数—1。通过数形结合这样的方式，揭示了问题的本质，使学生更易理解，树立了学生的数学自信，提高了学生的逻辑思维能力。

二、以数辅形，拓展思维

“形”的优势是直观形象，但缺少“数”的精准刻画，就难以准确表达。所以以简洁的数学描述、形式化的模型才能更好的体现数学抽象化和形式的魅力。

比如对几何图形的判断：比较周长相等的长方形和圆，哪个图形的面积大？如果仅仅图形的对比很难辨别出哪个的面积大，这个时候就需要“数”的精准刻画。假如两个图形的周长都是20厘米，那么正方形的面积等于（20÷4）2=25平方厘米，圆面积等于3.14X（20÷6.28）2≈31.8平方厘米。比较31.8>25，由此得出圆的面积大。这样通过具体的数量之间的对比由此得出正方形和圆在周长相等的情况下，圆的面积大。所以正如数学家华罗庚说：“数缺形时少直观，形少数时难入微，数形结合百般好，隔离分家万事休”。只有“数”与“形”有机的结合，才能诠释其数形结合的魅力。

总之，数形结合思想是将抽象的数学语言与直观图形结合起来，使抽象思维与形象直观结合起来，让数学思维直观的表达，更便于理解、分析、解答问题。所以数形结合不仅能使概念本质化、解题过程简单化、学生学习主动化，还能发展学生的空间观念和形象思维，更好地展现知识的建构过程。教师在教学中有机的渗透数形结合思想，能激发学生的学习兴趣，提高学生的数学思维能力和数学素养，促进学生情感、态度、价值观的发展。

参考文献：

[1]林丽静. 浅析数形结合思想在小学数学教学中的应用策略[J].2021.

[2]何丽岩. "浅析数形结合思想在小学数学教学中的应用."（2019）.