基于非等覆盖半径的前置仓选址

赵琨　赵刚　赵永健　梁晨

摘要：为解决城市物流配送中心出现的配送效率低的问题，研究配送中心前置仓选址问题。基于非等覆盖半径思想，结合前置仓选址特性，建立以企业总成本最低和客户满意度最高为目标的前置仓选址优化模型。结合第二代非支配排序遗传算法（nondominated sorting genetic algorithm Ⅱ， NSGAⅡ）与差分进化（differential evolution， DE）算法对模型进行求解。利用Python进行算例分析，得出企业总成本与客户满意度之间的Pareto解集，给出Pareto解集在二维空间的分布。该研究可为不同类型企业提出多种前置仓选址方案。

关键词：  前置仓; 非等覆盖半径; 多目标遗传算法; 客户满意度

中图分类号：  U113;F272文献标志码：  A

Location selection of front warehouses based on

unequal coverage radius

Abstract： In order to solve the problem of low distribution efficiency in urban logistics distribution centers， the location issue of distribution centers’ front warehouses is studied. Based on the idea of the unequal coverage radius， combined with the characteristics of the front warehouse location， a front warehouse location selection optimization model with the goals to minimize the total cost of an enterprise and maximize the customer satisfaction is established. The model is solved combined with the nondominated sorting genetic algorithm Ⅱ （NSGAⅡ） and the differential evolution （DE） algorithm. Through the example analysis by Python， the Pareto solution set between the enterprise total cost and the customer satisfaction is obtained， and the distribution of the Pareto solution set in the twodimension space is given. The research can propose a variety of front warehouse location selection solutions for different types of enterprises.

Key words： front warehouse; unequal coverage radius; multiobjective genetic algorithm; customer satisfaction

引言

21世紀以来，中国电子商务产业迅速兴起，市场规模逐年扩大[1]，2014年全国线上零售额仅27 898亿元，到2019年已增长至106 324亿元[2]。城市交通压力的不断增加，以及新制造模式和新零售模式的不断发展，对城市快速物流配送提出了新的要求，前置仓就在这种情况下应运而生。前置仓是一种仓配模式，中央大仓只需对门店供货，就能够覆盖“最后一公里”，具有距离客户近、辐射范围有限、选址相对灵活、初期资金投入高等特性。前置仓可以满足客户的及时化、分散化、定制化需求[3]，因此探讨和研究前置仓的选址问题具有重要的理论与实践意义。

目前前置仓可分为两大类：一类是以大型电商企业为主体，采用“总仓+分仓”二级仓储形式布局，此类前置仓仓储规模较大，辐射半径可达600 km左右;另一类是基于O2O服务模式的电商，采用“城市配送中心+前置仓”的模式，将前置仓布局在市中心，此类前置仓的规模较小，仓储面积为80～100 m2，辐射半径一般在3～5 km。相较于传统的选址问题，前置仓选址一般选在离消费者较近但人流量很少的地方，比如某个办公楼或者社区内的小型仓库等;由于前置仓仅提供配送服务而不对外营业，所以前置仓的选址对地理位置的要求很低，选址时只需要做到覆盖住户数量大、环境有利于货物储存即可。

国内外学者对物流设施选址问题进行了深入研究，已经取得了诸多成果。周愉峰等[4]建立了一个适用于震后救援初期的应急设施选址分配模型，并设计了一种混合遗传算法进行求解。赖志柱等[5]建立了多目标应急物流中心选址的确定型模型和鲁棒优化模型。马云峰等[6]建立了考虑时间满意度的选址模型，并提出拉格朗日松弛求解算法。肖建华等[7]提出非等覆盖半径选址概念，设计一种基于自适应遗传算法的动态膜算法求解模型。陈诚等[8]建立了基于分级顾客满意度的选址路径优化模型。武明帅等[9]建立了以配送中心总成本最低为目标函数的选址模型，应用布谷鸟算法进行求解。李茂林[10]提出一种基于非线性调节因子的猴群优化算法对选址模型进行优化。倪卫红等[11]以新冠肺炎为背景，采用聚类重心法对应急物流配送中心选址问题进行研究。

最大覆盖选址问题（maximal covering location problem，MCLP）已被证明是最有用的选址模型之一。传统的最大覆盖选址模型更多从企业的角度建立模型，并且存在各设施点的最大覆盖半径难以确定的问题，同时在传统的最大覆盖选址模型中，所有设施点的覆盖半径均相同，较少考虑需求点的不同参数对设施点覆盖半径的影响。前置仓设置在城市中，需要根据实际情况对各个前置仓的覆盖范围进行灵活调整，因此对选址模型中设施点覆盖半径的确定有着较高的要求。本文引入非等覆盖半径的思想，结合前置仓的特性，构建基于非等覆盖半径的前置仓选址模型。结合第二代非支配排序遗传算法（nondominated sorting genetic algorithm Ⅱ， NSGAⅡ）与差分进化（differential evolution， DE）算法对模型进行求解。本文将该组合算法记为DENSGAⅡ。通过算例验证模型和算法的有效性和可行性。

1基于非等覆盖半径的前置仓选址模型构建该模型主要包括各需求点的最大选址半径计算、前置仓候选区域确定、前置仓数量确定和前置仓选址优化模型构建四部分。

1.1需求点的最大选址半径计算

候选区域的人口状况、经济状况等直接影响前置仓的选址。因此，选择候选区域人口状况作为关键指标来确定各需求点的最大选址半径。

候选区域人口状况主要从人口密度、人口年龄结构和人口性别结构方面来描述。

人口密度。前置仓的选址不仅需要考虑人口规模，还需要结合土地面积综合分析人口在一定区域的分布。本文将人口密度分为五级，由一级到五级人口密度递减。用ki表示需求点i的人口密度等级，ki∈{1，2，3，4，5}，ki越小，该需求点的人口密度就越大。

人口年龄结构。生鲜电商主要消费群体的年龄为20～35岁，年龄稍大的人群主要通过菜市场、线下实体水果店等满足需求。用αi表示需求点i的20～35岁人口数占总人口数的比例。

人口性别结构。一般认为女性较男性有更明显的消费动机，但事实并非如此。统计数据显示，2019年男性使用生鲜电商产品的比例为60.3%，略高于女性。用ρi表示需求点i的女性数量占比。

在客户实际下单过程中，客户可能会选择自提或进店消费（例如叮咚买菜、盒马鲜生等），此时订单不需要配送，但并不会影响以配送业务为主的前置仓选址。自提或进店消费占比λi=（qi-q′i）/qi，这里qi为需求点i的需求量，q′为需求点i的配送量。

在实际配送过程中，需求点的最大配送服务半径与配送运输速度相关，而配送运输速度又与路况系数有关。本文引入需求影响因子μi，则需求点i的最大配送服务半径可表示为 式中：wi和li分别为需求点i的人口年龄结构和人口性别结构影响因子，且wi+li=1;ri为路况系数，ri ∈[0，1]，路况越好，前置仓服务半径越大;vi为平均运输速度。

1.2前置仓候选区域确定

利用求解出的需求点最大配送服务半径和平面圓交集覆盖理论，确定前置仓候选区域。Ci表示以需求点i为圆心，以βi为半径的圆;（xi，yi）为需求点i的位置;d′ij为需求点i到需求点j的距离。

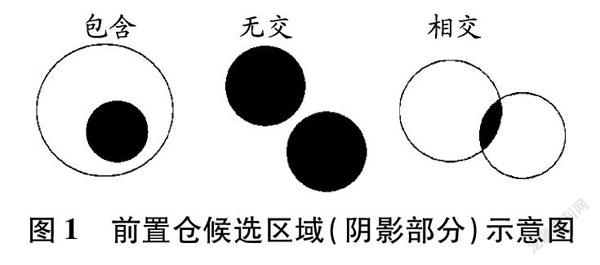
每个需求点所对应的配送中心必须位于该需求点的最大配送服务半径内，才能满足需求点的需求。对于2个需求点，基于非等覆盖半径思想，对前置仓候选区域分3种情况讨论，见表1。前置仓候选区域示意图见图1。

在实际选址中，假设有n个需求点，每个需求点的最大配送服务半径和位置坐标已知，则n个需求点对应的Ci是否相交的判断可以转化为求解以下不等式组是否有解：

若不等式组有解，则可在交集区域建立前置仓，否则需建立多个前置仓来满足需求。

1.3前置仓候选区域中的前置仓数量确定

前置仓选址具有灵活性，可以在已知的候选区域充分利用闲置、偏僻的物业、地下室等资源，因此可先对候选区域内可用作前置仓的位置进行粗选，再利用数据包络分析法、层次分析法等定量方法进行细选，按比例选出一定的前置仓候选点。一般在每个候选区域内，选择2～3个候选点即可。

1.4前置仓选址优化模型构建

前置仓选址优化问题属于一个NP难问题。模型假设如下：仅在前置仓候选区域内进行选址;为前置仓配送货物的配送中心位置确定，且货量充足;已知每个需求点的位置和需求，并在一段时间内需求无波动;每个需求点有且仅有一个前置仓为其提供配送服务;已知各候选前置仓的建设费用和运营管理费用;忽略竞争对前置仓选址的影响;忽略货物在运输过程中的损耗;忽略天气因素的影响。

符号和变量说明：I为需求点集合（也为顾客集合），i∈I;J为前置仓集合，j∈J;S（tij）为顾客i对前置仓j的配送时长满意度函数;p为要设置的前置仓个数;qi为需求点i的需求量;mj为前置仓j的最大货物储存量;Qj为前置仓j的最大处理能力;Aj为前置仓j的建设成本;Bj为前置仓j单位产品的运营成本;dij为需求点i到前置仓j的距离;dj为配送中心到前置仓j的距离;cij为从前置仓j到需求点i的单位运费;cj为从配送中心到前置仓j的单位运费;xij为01变量，xij=1表示前置仓j可以覆盖需求点i，否则xij=0;yj为01变量，yj=1表示在候选点j设置前置仓，否则yj=0。

通过上述对前置仓选址特点的分析，从企业角度和客户角度出发，确立两个目标：企业总成本最低和客户满意度最高。由于前置仓选址对时间的敏感度较高，故需要选择一种能准确反映客户对时间偏好的满意度函数。根据前期调研可知：当配送时间超出客户可接受范围时，客户将感到十分不满意，严重降低客户对平台的忠诚度;当配送时间在客户可接受范围内时，客户满意度也会随配送时间增加而降低。因此，本文引入路况系数，选择凹凸时间等待成本函数来拟合客户满意度：式中：[T1，T2]为客户可接受的配送时间窗;η为时间敏感系数;货物从前置仓j配送到顾客i的时刻tij=dij/（rivi）。

综上，综合企业总成本最低和客户满意度最高的前置仓选址模型如下：（1）

（2）（3）

（4）

（5）

（6）

xij∈{0，1}，yj∈{0，1}（7）式（1）和（2）为2个目标函数：式（1）表示企业总成本最低，该成本包括前置仓建设成本、从配送中心到前置仓的配送成本、前置仓运营成本和从前置仓到客户的配送成本;式（2）表示客户满意度最高。式（3）～（7）为约束条件：式（3）表示顾客的总需求量不超过前置仓的最大处理能力;式（4）表示设置的前置仓数量小于候选前置仓数量p;式（5）限制每个需求点只能被一个前置仓覆盖;式（6）表明前置仓与需求点之间的关系，需求点只能在前置仓被选中时才被该前置仓覆盖;式（7）是对决策变量的01约束。

2模型求解算法

前置仓选址优化问题多采用启发式算法求解。NSGAⅡ算法在运行后期易出现收敛速度慢的情况，故利用DE算法良好的全局搜索能力进行弥补;NSGAⅡ算法的快速非支配排序和种群多样性保持策略可以很好地弥补DE算法容易丢失Pareto解的问题：故将两种算法组合，命名为DENSGAⅡ算法[12]。算法基本流程见图2。

步骤1将种群个体进行非支配排序分层，见图3。搜索非支配个体集的具体步骤如下：①选定个体i;②对于种群中其他所有的个体j，按照Pareto最优比较个体i与j之间的支配与非支配关系;③若不存在任何一个个体j优于i，则标记个体i为非支配个体;④遍历所有个体，直到找出所有的非支配个体。

通过上述步骤得到的非支配个体集是种群的第一级非支配层;忽略这些已标记的非支配个体，再遵循步骤①～④，就会得到第二级非支配层;以此类推，直到整个种群被分层。

步骤2同层个体拥挤度比较，见图4。

设每个个体的拥挤度为0;针对每个目标，对种群进行非支配排序，令边界的两个个体拥挤度为无穷;对其他的个体i进行拥挤度的计算，计算式为2j=1Fj，i+1-Fj，i-1，其中Fj，i+1和Fj，i-1分别表示个体i+1和i-1的第j个目标值。

对种群个体进行非支配排序分层和同层拥挤度计算后，每个个体都会得到两个属性：所属的非支配层和拥挤度。在个体i与j的比较中，个体i只要符合下面的一个条件，则个体i获胜：（1）个体i所处的非支配层优于个体j所处的非支配层;（2）i、j处于相同层级，但个体i比个体j的拥挤度大。第一个条件确保被选择的个体属于较优的非劣等级。对于处于同一非劣等级而不分胜负的两个个体，第二个条件确保选择位于较不拥挤区域的个体（有较大拥挤度的个体）。胜出的个体进入下一步操作。

步骤3进行DE算法的变异、交叉、选择操作确定子代个体，具体步骤如下：

①对候选前置仓采用01编码方式编码，生成初始种群。

②采用随机引导变异方法对种群进行变异操作：式中：下标i表示第i个个体;下标G表示第G代种群;下标r1，r2和r3分别表示第G代的第r1、r2和r3个个体;xi，G是目标向量;vi，G是变异向量;Fi为缩放因子，用于对差分向量进行缩放，控制搜索步长。

③交叉操作。将生成的变异向量vi，G与目标向量xi，G进行交叉，得出实验向量ui，G。本文采用的二项式交叉方式如下：

xij，G，其他式中：下标“ij，G”表示第G代种群中第i个个体的第j个基因，j=1，2，…，D;rij表示第i个个体的第j个基因对应的[0，1]内的随机数;jrand为[1，D]内的一个随机整数;Cr为交叉概率，用来控制算法的收敛速度，Cr∈[0，1]。

④选择操作。采用高强度贪婪选择策略，将目标向量与实验向量进行逐一比较，胜出者为本代子代个体，方法如下：其他步骤4精英选择策略。在NSGAⅡ算法中，将父代与子代中所有个体混合后进行非支配排序，可较好地避免父代中优秀个体的流失[13]。精英选择策略如图5所示：先将第t代迭代后产生的新种群Qt与父代种群Pt合并成种群Rt，种群规模为2N;然后对种群Rt进行非支配排序，产生一系列非支配解集Zi并进行拥挤度计算。因为子代和父代个体都包含在种群Rt中，经过非支配排序后得到的非支配解集Z1在所有非支配解集中是最优的，所以先将Z1放入新的父代种群Pt+1中。如果Pt+1的种群规模小于N，则向Pt+1中填充下一级非支配解集;若添加Z3时Pt+1的规模超出N，则对Z3中的个体进行拥挤度比较，选择拥挤度大的个体放入Pt+1中，直到Pt+1的规模达到N。

3数值实验

本节利用Python编程求解模型并分析求解结果。所有的工作均在一台计算机上完成。根据本节数值实验结果，确定算法的最大迭代次数、交叉概率、变异概率等参数。

3.1算法对比

从多个角度对比DENSGAⅡ与NSGAⅡ，测试DENSGAⅡ的稳定性以及优势。参数设置：最大迭代次数为5 000，交叉概率为0.8，变异概率为0.1。不同参数下的算法对比见表2。

从算法收敛性能看，DENSGAⅡ比传统的NSGAⅡ具有更好的收斂性能。从收敛次数看，NSGAⅡ的平均收敛次数是DENSGAⅡ的2倍左右，且求解问题的复杂度越高，DENSGAⅡ的收敛性能就越优。程序迭代动画显示，DENSGAⅡ在运行初期便可以较快地收敛到Pareto前沿面，而NSGAⅡ在运行后期也会存在Pareto前沿面刻画不完全的问题。

从算法求解时间看，DENSGAⅡ与NSGAⅡ的求解时间相差不大。然而，DENSGAⅡ的收敛性优于NSGAⅡ的，因此当需要达到同样的求解效果时，DENSGAⅡ的求解速度更快。当问题的复杂度足够高时，不宜采用最大迭代次数为算法结束条件，此种情况下更能凸显DENSGAⅡ的求解优势。

从得出的Pareto前沿解看，DENSGAⅡ得出的Pareto前沿解远多于NSGAⅡ的，较多的Pareto前沿解可以更好地描述多目标解空间的复杂度，更能进行精准的方案选择。

3.2最大迭代次数确定

算法的最大迭代次数主要与问题规模有关，本节只讨论在相同数量级情况下，候选前置仓个数与需求点个数对算法运行速度及结果的影响。

设种群内染色体的数目为100，交叉概率为0.8，变异概率为0.1。不同参数条件下DENSGAⅡ的收敛效果见表3。

综合算法求解时间、Pareto解个数以及问题规模，得出算法最大迭代次数设置范围为500～3 000，具体取值可根据问题规模灵活调整。

3.3交叉、变异概率确定

将交叉概率取不同值，将变异概率固定为0.10，计算候选前置仓个数为40、需求点个数为500时的Pareto解个数和算法求解时间。对表4结果进行分析，确定本算法交叉概率为0.90。

然后，将变异概率取不同值，将交叉概率固定为0.90，计算候选前置仓个数为40、需求点个数为500时的Pareto解个数和算法求解时间。对表5结果进行分析，确定本算法变异概率为0.10。

4算例

以某生鲜移动电商在太原市小店区进行前置仓选址为例。对该区80个需求点进行调研得到，该区平均运输速度为30 km/h，需求点的人口年龄结构和人口性别结构影响因子为[0，1]之间的随机数，自提或进店消费占比为0.15。需求点位置、需求量、客户可接受时间窗、路况系数、需求影响因子和人口密度等级等部分数据见表6。利用非等覆盖半径选址模型确定候选前置仓位置，并通过调研得出候选前置仓建设成本和运营成本，部分数据见表7。

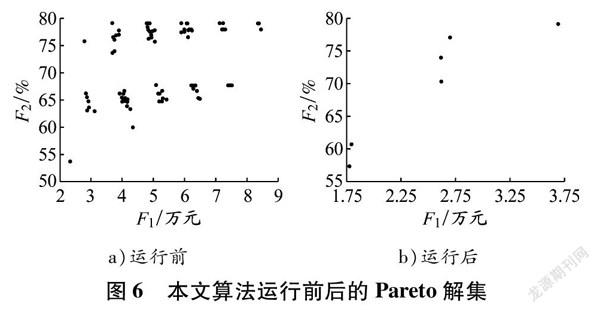
利用DENSGAⅡ算法，使用Python 3.0编程，在Intel（R） Core（TM） i510210U处理器和16 GB内存的硬件环境下运行，其中变异概率为0.10，交叉概率为0.90，种群密度为50，最大迭代次数为10 000，运行结果见图6。

考虑到实际选址中过低的客户满意度并无意义，从44个Pareto解集中选择客户满意度高于90%的20个选址方案作为候选方案，各方案前置仓选择、企业总成本及客户满意度见表8。

企业可以根据需要选择不同的前置仓选址方案：（1）若企业资金雄厚且侧重于提高客户满意度，则可选择方案15～20，这些方案的客户满意度高达99%。（2）若企业侧重于节省成本，则可选择方案1～6，这些方案不仅可使客户满意度达到90%以上，而且其选址成本也偏低。（3）若企业同时考虑客户满意度和企业总成本，则可选择方案7～14。

5结论

前置仓作为物流“最后一公里”问题的新的解决方案，其选址是否科学以及布局是否合理关系到整个供应链体系的成本和效率。多方面因素的考量、准确简单模型的建立、快速精确的求解算法、多样化方案选择对丰富前置仓选址模型以及指导企业合理实践具有重要意义。本文针对已有选址模型的不足，引入非等覆盖半径的思想，结合选址区域内人口密度、人口年龄结构、人口性别结构等特性，构建基于非等覆盖半径的前置仓选址模型。结合第二代非支配排序遗传算法（NSGAⅡ）与差分进化（DE）算法对模型进行求解。以某生鲜移动电商在太原市小店区的前置仓选址为例，得出多个前置仓选址方案，验证了模型和算法的合理性。

参考文献：

[1]何振绮， 陈宏志. 电子商务时代的企业国际供应链管理模式研究[J]. 物流技术， 2007， 26（8）： 144146.

[2]巴旭成. 我国生鲜电商新零售模式的研究[J]. 环渤海经济瞭望， 2020（3）： 2526.

[3]衡欢乐. 基于生鲜前置仓的选址研究[D]. 北京： 北京交通大学， 2019.

[4]周愉峰， 陈娜， 李志， 等. 考虑设施中断情景的震后救援初期应急物流网络优化设计[J]. 运筹与管理， 2020， 29（6）： 107112.

[5]赖志柱， 王铮， 戈冬梅， 等. 多目标应急物流中心选址的鲁棒优化模型[J]. 运筹与管理， 2020， 29（5）： 7483.

[6]马云峰， 杨超， 张敏， 等. 基于时间满意的最大覆盖选址问题[J]. 中国管理科学， 2006， 14（2）： 4551.

[7]肖建华， 王飞， 白焕新， 等. 基于非等覆盖半径的生鲜农产品配送中心选址[J]. 系统工程学报， 2015， 30（3）： 406416. DOI： 10.13383/j.cnki.jse.2015.03.011.

[8]陈诚， 檀晓琳， 邓颖. 基于分级顾客满意度的水果电商物流配送网络选址路径问题[J]. 华东交通大学学报， 2019， 36（4）： 8894. DOI： 10.16749/j.cnki.jecjtu.2019.04.012.

[9]武明帅， 王巍， 孙理越. 基于布谷鸟搜索算法的物流配送中心選址[J]. 经济师， 2021（2）： 252253， 255.

[10]李茂林. 基于改进猴群优化算法的物流配送中心选址研究[J]. 太原学院学报（自然科学版）， 2020， 38（2）： 4450. DOI： 10.14152/j.cnki.2096191X.2020.02.0010.

[11]倪卫红， 陈太. 基于聚类重心法的应急物流配送中心选址[J]. 南京工业大学学报（自然科学版）， 2021， 43（2）： 255263. DOI： 10.3969/j.issn.16717627.2021.02.017.

[12]李岩， 张光武. 混合NSGAⅡ和DE的优化算法及应用[J]. 哈尔滨理工大学学报， 2018， 23（5）： 7579. DOI： 10.15938/j.jhust.2018.05.013.

[13]许玉龙， 潘旭， 王忠义， 等. 利用帕累托非支配关系实现高效三目标差分进化的方法[J]. 计算机应用研究， 2019， 36（3）： 817823， 828. DOI： 10.19734/j.issn.10013695.2017.09.0909.

（编辑赵勉）

收稿日期： 20210321修回日期： 20210821

基金项目： 北京市社会科学基金（17GLB020）

作者简介： 赵琨（1978—），女，辽宁本溪人，副教授，硕导，博士，研究方向为物流工程、最优化方法、数据挖掘，（Email）piaopiao_zk@163.com