基于信息熵的船舶轨迹自适应分段压缩算法

杨家轩　马令琪　

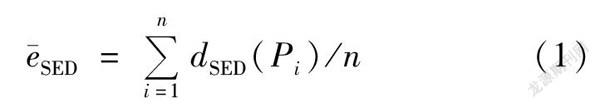
摘要：針对目前轨迹压缩研究仅考虑船舶位置而忽略船舶操纵特征以及目前轨迹分段研究需确定多种阈值等问题，提出一种基于信息熵的船舶轨迹自适应分段压缩算法。该算法综合考虑船舶位置、航向和速度等信息，引入信息熵作为评判轨迹特征点的指标，从船舶轨迹中提取分段关键点，进而自适应划分出多条子轨迹，再利用自顶向下时间比（topdown time ratio， TDTR）算法分别对子轨迹进行压缩。以老铁山水域船舶交通数据为实验样本，从压缩误差、运行效率等方面对比分段前后的轨迹压缩效果。结果表明，该算法能根据船舶的航向和速度信息对船舶轨迹进行自适应分段，分段后再压缩可大幅降低各种压缩误差，提升压缩效率，特别在轨迹数据量较大情况下效果更佳。

关键词：  船舶轨迹; 分段; 压缩; 信息熵

中图分类号：  U675.7;U697.3文献标志码：  A

An adaptive segmentation and compression algorithm of ship

trajectory based on entropy of information

Abstract： Aiming at the current trajectory compression research that only considers the ship position but ignores the ship maneuvering characteristics， and the current trajectory segmentation research that needs to determine multiple thresholds， an adaptive segmentation and compression algorithm based on the entropy of information is proposed. The algorithm comprehensively considers the ship position， heading and speed， introduces the entropy of information as an index to judge the trajectory feature points， extracts the key segmentation points from a ship trajectory to adaptively divide the trajectory into multiple subtrajectories， and then compresses subtrajectories separately using the topdown time ratio （TDTR） algorithm. The ship traffic data of Laotieshan waters are taken as the experimental sample， and the effects of trajectory compression before and after segmentation are compared in terms of the compression error and efficiency. The results show that， the algorithm can adaptively segment a ship trajectory according to the ship heading and speed information， and the segmentation compression can significantly reduce various compression errors and improve the compression efficiency， especially in the case of large amount of trajectory data.

Key words： ship trajectory; segmentation; compression; entropy of information

引言

海洋约覆盖了71%的地球表面，大多数国际贸易都是通过海运完成的。面对愈加复杂的海上航行环境，利用船舶自动识别系统（automatic identification system， AIS）感知海上态势越来越重要[1]。不同的船舶由于运动模式的不同，以大约2 s～6 min的时间间隔发送AIS信息，因此AIS数据量非常大[2]。为减少AIS数据处理过程中的存储和计算成本，通常需要对轨迹进行压缩。

目前，船舶轨迹压缩主要有在线压缩和离线压缩两类方法。在线压缩方法无须得到整艘船的轨迹。高邈等[3]将改进后的滑动窗（sliding window，SW）算法应用到AIS轨迹压缩中。SUN等[4]基于扫描拾取移动（scanpickmove，SPM）和SW的思想提出SWSPM算法。ZHANG等[5]提出一种考虑位置、方向和速度的在线多维船舶轨迹压缩算法。而离线压缩方法考虑完整的轨迹，比在线压缩方法更容易实现全局优化。道格拉斯普克（DouglasPeucker，DP）算法是一种常用的离线压缩方法。除地理位置信息之外，AIS数据还包含时间、速度、航向等重要信息[6]。一些学者在使用船舶位置进行船舶轨迹离线压缩的基础上拓展考虑了时间、速度、航向等其他信息。MERATNIA等[7]提出了自顶向下时间比（topdown time ratio， TDTR）算法，以同步欧氏距离（synchronous Euclidean distance， SED）代替欧氏距离对DP算法进行改进。QI等[8]提出一种识别船舶航向变化并提取船舶轨迹代表点的方法。ZHAO等[9]考虑轨迹点的航向信息，对DP压缩算法进行了改进。ZHU等[10]考虑轨迹点的位置、航向和航速，提出一种多维特征距离计算方法。根据航向和速度等信息对轨迹进行分段预处理可以使压缩轨迹保留航向和速度信息。YUAN等[11]提出一种基于轨迹转向角的分段方法，但该方法只考虑了轨迹方向的突变。何爱林等[12]考虑了转向角突变及其累计变化，但没有考虑速度因素。韩陈寿等[13]通过在给定距离内找轨迹的开放角和变速点对轨迹进行分段。金佳龙等[14]和盛凯等[15]提出基于船舶运动模式的轨迹分段算法。宋鑫等[16]在进行压缩前对轨迹进行了分段处理。这几种船舶轨迹分段方法虽然考虑了船舶的航向或速度信息，但需要人为确定航向阈值、速度阈值甚至时间阈值，不同的阈值对结果影响较大，因此具有一定局限性。F6AB678E-6402-4886-AC74-C9922E3EE7A6

对时间跨度长、空间跨度大、数据量极大的船舶轨迹进行压缩时，分段是必不可少的一步，以子轨迹段为分析对象也有利于发现轨迹的局部相似运动模式。因此，本文提出一种基于信息熵的船舶轨迹自适应分段压缩算法，根据船舶的航向和速度等特征对轨迹进行无须确定多种阈值的自适应分段，再对子轨迹段分别进行基于自适应阈值的TDTR压缩。

1基本定义和算法

1.1轨迹相关的基本定义

原始轨迹：原始AIS轨迹T为若干有序轨迹点数据的集合，可被表述为T={pii=1，2，…，n}，其中pi=（xi，yi，ti，ci，si），xi、yi、ti、ci和si分别代表第i个轨迹点所对应的经度、纬度、时刻、航向和速度。

压缩轨迹：对原始轨迹T采用压缩算法删除若干轨迹点（除首、尾点）后得到的轨迹，用T′表示，T′={p′ii=1，2，…，m;m≤n}。

子轨迹：在原始轨迹T（或压缩轨迹T′）中，任意两点之间轨迹点组成的轨迹称为T（或T′）的子轨迹。

1.2压缩性能评估方法

轨迹压缩会带来不同维度上的损失[17]。本文选取航向误差、SED误差、速度误差、压缩率、运行时间等5个指标评估轨迹压缩算法的性能。

定义压缩率为r=1-T′/T，其中T代表原始轨迹点的数目，T′代表压缩后轨迹点的数目。运行时间指对轨迹进行压缩需要的时间，是衡量压缩算法执行效率的重要依据。

平均SED误差SED的计算公式为                             （1）式中：Pi指原始轨迹中的第i个点;n指原始轨迹点数。当Pi被保留在压缩后的轨迹中时，dSED（Pi）=0;当Pi未被保留在压缩后的轨迹中时，dSED（Pi）为以压缩后轨迹上Pi前后两个相邻的点为基准点计算的Pi的同步欧氏距离。

平均航向（或速度）誤差指原始轨迹中每个点的航向（或速度）误差的平均值。当Pi被保留在压缩后的轨迹中时，Pi的航向（或速度）误差为0;当Pi未被保留在压缩后的轨迹中时，Pi的航向（或速度）误差为Pi的航向（或速度）与压缩后轨迹上Pi前后两个相邻点的平均航向（或速度）差值的绝对值。

1.3TDTR算法

TDTR算法是一种基于DP算法的考虑全局特征的压缩算法。不同于DP算法直接采用欧氏距离作为压缩衡量标准，TDTR算法采用的是SED。SED是一种将位置和时间考虑在内的距离度量，如图1所示，点Pm的SED（用dSED（Pm）表示）为点Pm与其同步点P′m之间的欧氏距离，计算式如下：

（2）

（3）

（4）

2基于信息熵的轨迹分段算法

信息熵常被用来作为一个系统信息含量的量化指标，能衡量随机事件的不确定性。随机事件不确定性越高，信息熵值越大。设X是一个取有限值的离散随机变量，其概率分布为                             （5）则随机变量X的信息熵定义为                               （6）对于一条轨迹，当且仅当轨迹中每个轨迹点的某一特征均不同时，该轨迹这一特征的信息熵值最大。轨迹中至少有一个位置总是使两段子轨迹之间的差异最大，基于此，可对轨迹进行基于航向和速度特征的分段。进行基于信息熵的轨迹分段前需先利用k均值聚类算法获得轨迹的航向和速度区间，然后根据航向和速度区间确定轨迹的航向标签和速度标签。轨迹的航向信息熵En，course（T）计算式如下：                              （7）

（8）式中：Li，course为根据航向区间划分得到的航向标签;Lcourse为航向标签总数;N（Li，course）为Lcourse中某一相等标签出现的总次数;ci表示各类航向标签在Lcourse中出现的频率。速度信息熵En，speed（T）计算式如下：（9）

（10）式中：Li，speed为根据速度区间划分得到的速度标签;Lspeed为速度标签总数;N（Li，speed）为Lspeed中某一相等标签出现的总次数;si表示各类速度标签在Lspeed中出现的频率。

将轨迹T1，n-1在第i（1≤i≤n-1）个轨迹点处进行分段，分成两段子轨迹T1，i和Ti+1，n-1，根据式（11）依次计算在不同的轨迹点处分段的信息熵En，split（T1，n-1）（以基于航向信息熵的分段为例），选择En，split（T1，n-1）值最小处为最终分段的位置。En，split（T1，n-1）=N1NEn，course（T1，i）+N2NEn，course（Ti+1，n-1）（11）式中：N1、N2和N分别代表T1，i、Ti+1，n-1和T1，n-1的轨迹点数。

基于信息熵的轨迹分段伪代码如下：

输入：k1，k2，T={p1，p2，…，pn}，En，threshold

输出：分段后的轨迹Taftersplit

/*第一阶段，从原始轨迹中获取轨迹的航向和速度信息*/F6AB678E-6402-4886-AC74-C9922E3EE7A6

1. for each point in T do

2. courselist.append（p[3]）/*获取航向信息courselist*/

3.speedlist.append（p[4]）/*获取速度信息speedlist*/

4. end for

/*第二阶段，基于k均值聚类的航向和速度区间获取*/

5. c←kmeans（k1，courselist）/*k均值函数将航向聚成k1类，得到k1个中心点*/

6. courseinterval←c.sort（）/*对k1个航向中心点升序排列，得到航向区间courseinterval*/

7. s←kmeans（k2，speedlist）/*k均值函数将速度聚成k2类，得到k2个中心点*/

8. speedinterval←s.sort（）/*对k2个速度中心点升序排列，得到速度区间speedinterval*/

/*第三阶段，对轨迹进行考虑航向的划分*/

9. Lcourse←courseinterval（courselist）/*根据航向区间，得到航向标签Lcourse*/

10. entropycourse←En，course/*计算航向信息熵entropycourse*/

11. if entropycourse≥En，threshold then

12. find min（En，split（T））/*找到最小En，split，在该点处进行分段*/

13. Tcourse1←T1，i/*该点之前的点组成一条轨迹段Tspeed1*/

14. Tcourse2←Ti+1，n-1/*该点之后的点组成一条轨迹段Tcourse2*/

15. else

16. Tcourse1←T/*该轨迹无须分段*/

17. Tcourse3←Tcourse1 1，i/*对Tcourse1和Tcourse2继续上述分段操作，得到新子轨迹Tcourse3和Tcourse4*/

18. Tcourse4←Tcourse1 i+1，n-1

19. Taftercoursesplit←{Tcourse1，Tcourse2，…，Tcoursem}/*Taftercoursesplit為经过航向信息熵分段的子轨迹*/

/*第四阶段，对轨迹进行考虑速度的划分*/

20. for each trajectory T′ in Taftercoursesplit do

21. Lspeed←speedinterval（speedlist）/*根据速度区间，得到速度标签Lspeed*/

22. entropyspeed←En，speed（Lspeed）/*计算速度信息熵entropyspeed*/

23. if entropyspeed≥En，threshold then

24. find min（En，split（T′））/*找到最小En，split，在该点处进行分段*/

25. Tspeed1←T′1，i/*该点之前的点组成一条轨迹段Tspeed1*/

26. Tspeed2←T′i+1，n-1/*该点之后的点组成一条轨迹段Tspeed2*/

27. else

28. Tspeed1←T′/*该轨迹无须分段*/

29. Tspeed3←Tspeed1 1，i/*对Tspeed1和Tspeed2继续上述分段操作，得到新的子轨迹Tspeed3和Tspeed4*/

30. Tspeed4←Tspeed1 i+1，n-1

31. Taftersplit←{Tspeed1，Tspeed2，…，Tspeedn}

32. end for

33. end

在利用k均值聚类算法对各轨迹点的航向和速度进行聚类时，需要确定k值，即确定得到几个航向或速度区间。为确保分段前后TDTR算法压缩性能对比的合理性，本文将轨迹分段数控制在10以内。将航向聚类数k1分别取1、2、3与速度聚类数k2分别取1、2、3的聚类结果进行两两组合，选取将轨迹分段数控制在10以内且分段数最多的k1、k2值。基于信息熵的分段无须确定航向阈值、速度阈值或者时间阈值，只需一个信息熵阈值En，threshold，阈值越小，分段越精细。比如，阈值设为0时，信息熵分段算法可以将包含n个轨迹点的轨迹分成n-1段（即每两个相邻轨迹点之间的轨迹为一条子轨迹）。3实验和结果

3.1实验数据来源

实验数据来自20170310至20170311老铁山水域的部分船舶轨迹。船舶轨迹及船舶速度变化情况（颜色越深对应速度越大，颜色越浅对应速度越小）见图2。

3.2轨迹分段效果展示

本文设置En，threshold=0.3。为证明分段算法的合理性，可视化呈现了3条代表性船舶轨迹的分段结果，见表1。由表1可以看出：轨迹a的船舶航向几乎没有变化，基于航向信息熵的处理没有对轨迹a分段，基于速度信息熵的处理把轨迹a分为2段，分段处的船舶速度变化较明显。轨迹b比较曲折，基于航向信息熵的处理将其在明显弯曲处分成4段子轨迹。由于轨迹b上船舶速度几乎没有变化，基于速度信息熵的分段处理没有得到新的子轨迹。轨迹c上船舶航向和速度变化都比较大，基于航向信息熵的处理将其在航向变化较大处分成4段，后续基于速度信息熵进一步将其分段，最终得到5段子轨迹。

利用基于信息熵的分段方法分别对轨迹进行考虑航向信息和速度信息的分段，可得到轨迹的航向和速度特征点，即子轨迹段的起止点。文献[16]提出了航向和速度特征点检测方法，即若某点与相邻点的距离差值、航速差值、航向差值均大于各自对应的阈值，则称该点为特征点。选取MMSI为636011643的船舶轨迹（见图3）进行对比实验，比较用文献[16]方法与基于信息熵检测方法检测出的特征点，结果见图4。文献[16]将航向阈值和速度阈值分别设为5°和5 kn，但该阈值并不适用于MMSI为636011643的船舶轨迹，本文依据该轨迹情况重新设定阈值。基于航向信息熵对该轨迹进行分段，可以看到5个航向特征点位于明显弯曲的位置，如图4a所示。图4b和4c为用文献[16]的方法在设置不同航向阈值时得到的结果。由图4b可以看出，用该方法可以检测到若干航向特征点，但检测出的特征点缺乏代表性。由图4c可以看出，在航向阈值为2°时仅能检测出该轨迹的一个航向特征点，可表1代表性轨迹分段结果呈现轨迹原始轨迹速度变化情况根据航向分段后的轨迹根据速度分段后的轨迹abcF6AB678E-6402-4886-AC74-C9922E3EE7A6

见检测结果易受航向阈值影响。用基于速度信息熵的方法检测出4个速度特征点（见图4d），结合图3可看出检测结果的合理性，即速度明显变化处被认定为速度特征点。而用文献[16]的方法检测得到的结果差别大，在速度阈值为0.1 kn时仅能检测出一个速度特征点，在速度阈值为0.2 kn时未能检测出速度特征点。这是因为该船的速度变化缓慢，其相邻轨迹点之间速度变化均没有超过0.2 kn。

综上可知，相比于其他需要人为确定航向或速度阈值的特征点检测方法，基于信息熵的检测方法可以自适应地对轨迹特征点进行检测，且效果不受航向或速度变化幅度的影响，检测出的特征点更具有代表性。

3.3分段压缩和不分段压缩对比实验

利用TDTR算法分别对未分段轨迹和分段后轨迹进行压缩，压缩阈值根据文献[18]提出的自适应分数来确定。该分数表示每一次轨迹压缩后误差比分与轨迹点数比分之和，分数越低表示轨迹压缩效果越好。分段前后轨迹压缩性能的对比结果见表2。由表2可知，在压缩率略微降低的情况下，无论是在压缩耗时还是在各种误差方面，对分段后轨迹进行压缩的结果都大大优于对未分段轨迹进行压缩的结果。

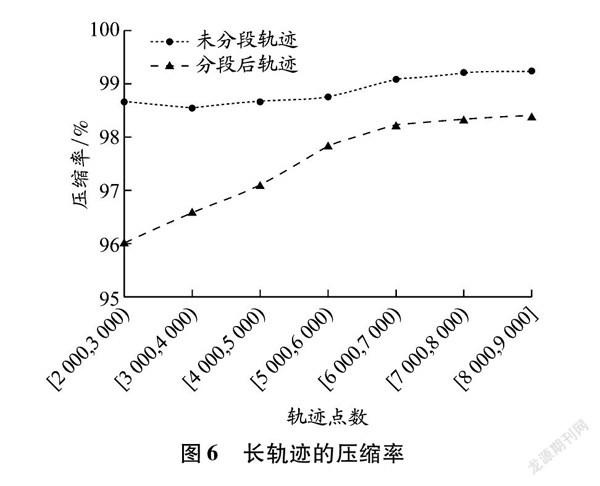
根据轨迹点数将轨迹分成短轨迹、中等轨迹和长轨迹三类（见表3），其中轨迹长度指一条轨迹所有相邻轨迹点之间距离的累加值。计算各类轨迹的压缩误差和压缩率的平均值，结果见图5。从航向误差、速度误差和SED误差来看，随着轨迹数据量的增大，无论是未分段轨迹还是分段后轨迹的压缩误差都逐渐增加。相比较而言，分段后轨迹的各种压缩误差增幅很小且一直明显低于未分段轨迹的压缩误差，尤其是SED误差。从压缩率来看，虽然未分段轨迹的压缩率一直高于分段后轨迹的压缩率，但未分段轨迹的压缩率随着数据量的增大没有明显变化，而分段后轨迹的压缩率随着数据量的增加却在缓慢增加，逐渐逼近未分段轨迹的压缩率。为证实这一点，对轨迹点数超过2 000的其他水域的长轨迹进行进一步实验，结果见图6。随着轨迹点数的增加，分段后轨迹与未分段轨迹的压缩率差距逐渐减小。因此，无论是从压缩误差还是从压缩率都可以看出，分段后轨迹压缩性能的优越性随着轨迹长度的增加越来越明显。

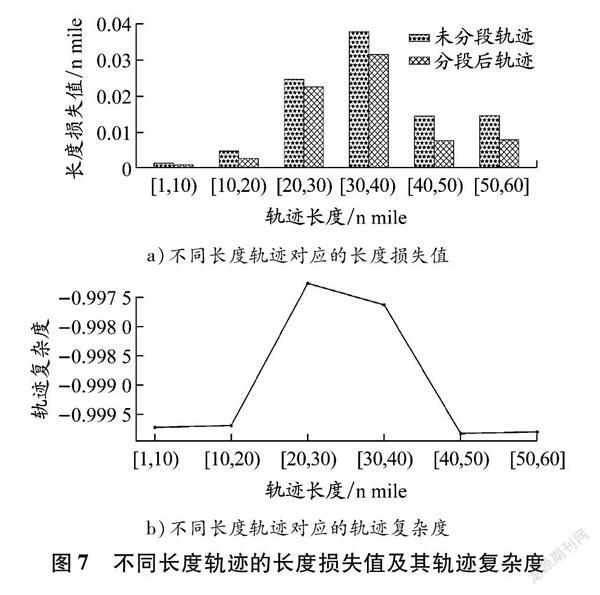
由于AIS发送数据的频率随船舶状态的变化而变化，轨迹点数多并不一定代表轨迹长。由表2也可知，部分中等轨迹的长度小于短轨迹，部分长轨迹的长度小于中等轨迹。因此，本文利用轨迹长度损失值对分段后轨迹和未分段轨迹压缩性能进行对比。轨迹长度损失值指原始轨迹与压缩后轨迹的实际长度差值。将轨迹按实际长度分为不同数据集并计算轨迹长度损失值，统计结果见图7。由图7可以看出：分段后轨迹的长度损失值一直小于未分段轨迹的长度损失值。整体上看，轨迹长度损失值随着轨迹长度的增加而增加，但20～40 n mile的轨迹长度损失值异常大。这是因为这一部分轨迹的复杂度较大，如图7b所示。轨迹复杂度为每个轨迹点拐角余弦的平均值，主要反映轨迹的弯曲程度，其值越大说明轨迹越曲折。

运行时间是衡量轨迹压缩效果的另一重要指标，图8为轨迹分段前后压缩耗时。由图8可知：轨迹分段前后压缩耗时都随着轨迹点数量的增加而增加;分段后轨迹压缩耗时明显低于未分段轨迹压缩耗时，且差距随着轨迹点数量的增加而增加，这说明

对长轨迹进行分段预处理是必要的。图9展示了自适应确定TDTR压缩阈值的计算时间。由图9可以看出：对轨迹分段后再压缩的计算效率较高;对未分段轨迹的自适应阈值计算时间随轨迹点数量的增加显著增加，而对分段后轨迹的阈值计算时间增加量不大，这是因为自适应阈值的计算需要迭代到每一个轨迹点，轨迹点越多，计算阈值的耗时必然越久。

4结论

针对船舶轨迹压缩算法忽略操纵信息和分段算法确定阈值难的问题，引入信息熵理论，考虑速度和航向，提出一种基于信息熵的船舶轨迹自适应分段压缩算法。采用老铁山水域的部分船舶轨迹数据进行对比实验，结果表明，该算法可以对船舶轨迹进行合理的分段。相比于未分段轨迹压缩，在压缩率略微降低的情况下，对轨迹分段后再压缩可大幅降低压缩误差和运行时间，且随着轨迹数据量的增加性能更好。在处理规模巨大的轨迹时，船舶轨迹的自适应分段压缩算法表现出更好的性能，这对海上交通态势感知和船舶交通信息的挖掘具有重要价值。

参考文献：

[1]WU X B， WU L， XU Y J， et al. Vessel trajectory partitioning based on hierarchical fusion of position data[C]//Proceeding of IEEE 18th International Conference on Information Fusion. IEEE， 2015： 12301237.

[2]SHENG P， YIN J B. Extracting shipping route patterns by trajectory clustering model based on automatic identification system data[J]. Sustainability， 2018， 10（7）： 2327. DOI： 10.3390/su10072327.

[3]高邈， 史國友， 李伟峰. 改进的Sliding Window在线船舶AIS轨迹数据压缩算法[J]. 交通运输工程学报， 2018， 18（3）： 218227. DOI： 10.19818/j.cnki.16711637.2018.03.022.

[4]SUN S， CHEN Y， PIAO Z J， et al. Vessel AIS trajectory online compression based on scanpickmove algorithm added sliding window[J]. IEEE Access， 2020， 8： 109350109359. DOI： 10.1109/ACCESS.2020.3001934.F6AB678E-6402-4886-AC74-C9922E3EE7A6

[5]ZHANG Y Q， SHI G Y， LI S， et al. Vessel trajectory online multidimensional simplification algorithm[J]. Journal of Navigation， 2019， 73（2）： 122. DOI： 10.1017/S037346331900064X.

[6]QI L， JI Y Y. Ship trajectory data compression algorithms for automatic identification system： comparison and analysis[J]. Journal of Water Resources and Ocean Science， 2020， 9（2）： 4247. DOI： 10.11648/j.wros.20200902.11.

[7]MERATNIA N， DE BY R A. Spatiotemporal compression techniques for moving point objects[C]//International Conference on Advances in Database Technology. DBLP， 2004： 765782. DOI： 10.1007/9783540247418_44.

[8]QI L， ZHENG Z Y. Vessel trajectory data compression based on course alteration recognition[J]. International Journal of Simulation： Systems， Science & Technology， 2016： 18. DOI： 10.5013/IJSSST.a.17.01.05.

[9]ZHAO L B， SHI G Y. A method for simplifying ship trajectory based on improved DouglasPeucker algorithm[J]. Ocean Engineering， 2018， 166： 3746. DOI： 10.1016/j.oceaneng.2018.08.005.

[10]ZHU F X， MIAO L M， LIU W. Research on vessel trajectory multidimensional compression algorithm based on DouglasPeucker theory[J]. Applied Mechanics and Materials， 2014， 694： 5962. DOI： 10.4028/www.scientific.net/AMM.694.59.

[11]YUAN G， XIA S X， ZHANG L， et al. An efficient trajectoryclustering algorithm based on an index tree[J]. Transactions of the Institute of Measurement & Control， 2012， 34（7）： 850861. DOI： 10.1177/0142331211423284.

[12]何爱林， 周德超， 陈萍， 等. 基于轨迹聚类的运动趋势分析[J]. 海军工程大学学报， 2017， 29（5）： 103107. DOI： 10.7495/j.issn.10093486.2017.05.022.

[13]韩陈寿， 夏士雄， 张磊， 等. 基于速度约束的分段轨迹聚类算法[J]. 计算机工程， 2011， 37（7）： 219221. DOI： 10.3969/j.issn.10003428.2011.07.074.

[14]金佳龙， 周伟， 姜佰辰. 基于行为模式的海上目标轨迹分段算法[J]. 信号处理， 2020， 36（12）： 115. DOI： 10.16798/j.issn.10030530.2020.12.014.

[15]盛凯， 刘忠， 周德超， 等. 基于运动模式的船舶轨迹分段压缩算法[J]. 海軍工程大学学报， 2018， 30（6）： 5057. DOI： 10.7495/j.issn.10093486.2018.06.009.

[16]宋鑫， 朱宗良， 高银萍， 等. 动态阈值结合全局优化的船舶AIS轨迹在线压缩算法[J]. 计算机科学， 2019， 46（7）： 333338. DOI： 10.11896/j.issn.1002137X2019.07.051.

[17]梁明， 陈文静， 段平， 等. 轨迹压缩的典型方法评价[J]. 测绘通报， 2019（4）： 6064. DOI： 10.13474/j.cnki.112246.2019.0113.

[18]LIN C Y， HUNG C C， LEI P R. A velocitypreserving trajectory simplification approach[C]//2016 Conference on Technologies and Applications of Artificial Intelligence. IEEE， 2016： 5865. DOI： 10.1109/TAAI.2016.7880172.

（编辑贾裙平）

收稿日期： 20210519修回日期： 20210917

基金项目： 国家自然科学基金（41861144014）;中央高校基本科研业务费专项资金（3132021154）

作者简介： 杨家轩（1981—），男，山东济宁人，副教授，博士，研究方向为海上交通工程、航海安全保障、AIS数据挖掘、水面无人航行器避碰等，（Email）yangjiaxuan@dlmu.edu.cnF6AB678E-6402-4886-AC74-C9922E3EE7A6