Encoding-Decoding-Based Recursive Filtering for Fractional-Order Systems
2022-06-25BoJiangHongliDongYuxuanShenandShujuanMu
Bo Jiang, Hongli Dong,,Yuxuan Shen, and Shujuan Mu
Corresponding author: Yuxuan Shen.
Citation: B. Jiang, H. L. Dong, Y. X. Shen, and S. J. Mu, “Encodingdecoding-based recursive filtering for fractional-order systems,”IEEE/CAA J.Autom. Sinica, vol. 9, no. 6, pp. 1103-1106, Jun. 2022.
The authors are with the Artificial Intelligence Energy Research Institute,Northeast Petroleum University, Daqing 163318, and the Heilongjiang Provincial Key Laboratory of Networking and Intelligent Control, Northeast Petroleum University, Daqing 163318, and also with the Sanya Offshore Oil & Gas Research Institue, Sanya 572025, China (e-mail: jiangbonepu@126.com; shiningdhl@vip.126.com; shenyuxuan5973@163.com; msj_4001@163.com).
Color versions of one or more of the figures in this paper are available online at http://ieeexplore.ieee.org.
Digital Object Identifier 10.1109/JAS.2022.105644
Dear editor,
This letter focuses on the encoding-decoding-based recursive filtering problem for a class of fractional-order systems. For the purpose of protecting security of the wireless communication network, a dynamic-quantization-based encoding-decoding mechanism is introduced to encrypt the transmitted measurement. Specifically, the measurement outputs are first encoded by the encoder into codewords which are then transmitted over the wireless communication network. After received by the decoder, the codewords are decoded and then sent to the filter. In light of the mathematical properties of truncated Gaussian distribution, the variance of the encoding-decoding-induced error between the decoded measurement and the real measurement is derived. An upper bound on the filtering error covariance is first obtained based on the variance of the encoding-decoding-induced error. Then, the minimal upper bound is derived by choosing proper filter gain. Finally, the efficiency and superiority of the proposed algorithm are verified through a simulation example.
The fractional calculus is a generalization of the integral calculus,which was first mentioned by Leibniz and Laplace hospital in 1695[1]. In recent decades, the fractional calculus has attracted great attention in the field of dynamic modeling and control engineering.In contrast to the classical integer calculus, the fractional calculus is able to model the complex systems more accurately. At the same time, some research results further demonstrate that the fractionalorder system has its unique advantages. For example, in [2], the dynamics of packet channels in TCP/IP networks has been described by fractional calculus, which provides a new mathematical idea for describing the characteristics of packet traffic behavior. The fractional-order model of ultracapacitors has been constructed to estimate the charge state more accurately in [3]. It is worth mentioning that the Kalman filter is regarded as an optimal estimator for solving the filtering problem of fractional-order system on account of the concise recursive form and excellent real-time online computing capability [4], [5].
On the other hand, with the rapid development of the wireless communication networks, the network security problem becomes a really hot research topic [6], [7]. To secure data from leakage and theft during transmission, the digital communication strategy has been widely used because of the high anti-interference and data encryption ability [8]. In recent years, the encoding-decoding mechanism (EDM) has received considerable research attention in the state estimation problems [9]-[12]. For example, in [13], a distributed filtering method for smart grid with concatenated coding is proposed to alleviate the limitation of communication resources. A multiple description video coding scheme is applied to heterogeneous communication chain to improve the robustness of video diversity[14]. Under the EDM, the encoder first maps the measurement into codewords according to specific rules, and the codewords are then transmitted to the decoder. The decoder restores the received codewords and sends the decoded information to the filter. Finally,the filter estimates the system state based on the decoded information. Due to the encoding-decoding process, the security of the measurement is improved to prevent attackers from stealing useful information.
It is worth noting that, although the EDM has unique advantages in improving the network security, there are also some noteworthy problems. Due to the introduction of the EDM, the decoded measurement might deviate from the real measurement. As such, the main challenges are identified as: 1) how to characterize the encodingdecoding-induced error between the decoded measurement and real measurement and 2) how to mitigate the filtering performance deterioration from the encoding-decoding-induced error should be seriously taken into consideration in the filtering problem under the EDM.In this letter, we aim to solve these two problems by considering the recursive filtering problem for the fractional-order system under the EDM. The main contributions of this letter are identified as: 1) the filtering problem is, for the first time, considered for the fractionalorder system under the EDM; 2) a random variable is introduced to represent the encoding-decoding-induced error, and the exact variance of the introduced random variable is calculated; and 3) a minimized upper bound is ensured on the filtering error covariance(FEC).
Problem formulation: Consider the following discrete fractionalorder system:





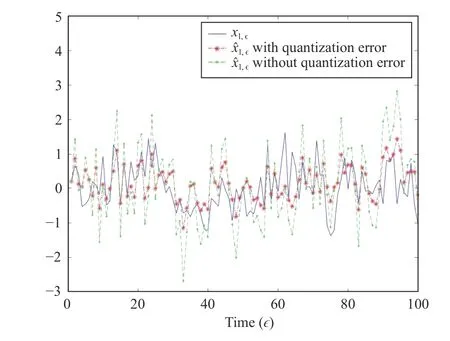
Fig. 1. State x1,ϵ and its estimate.
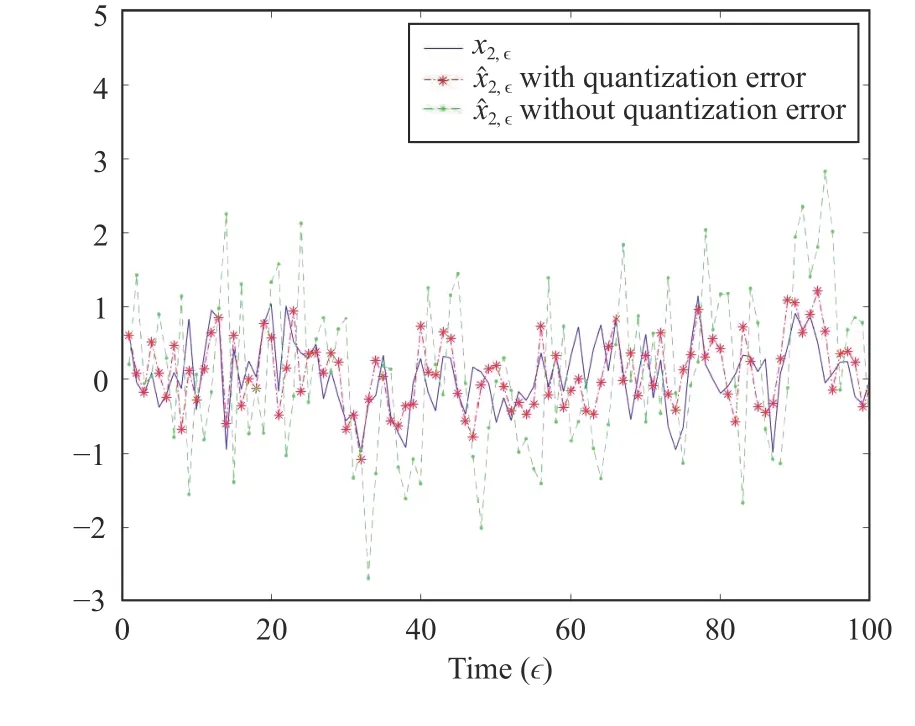
Fig. 2. State x2,ϵ and its estimate.
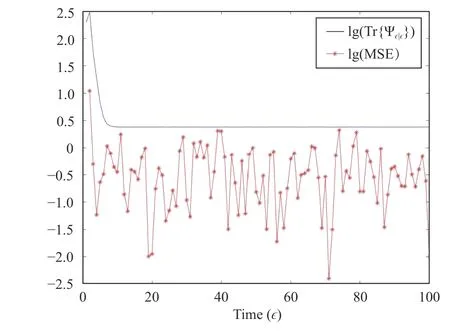
Fig. 3. The trace of Ψ ϵ|ϵ and the MSE.
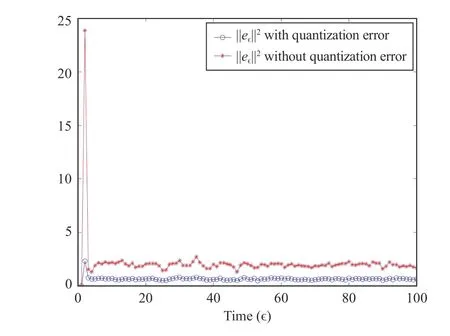
Fig. 4. Filtering error with and without quantization error.
Conclusions: In this letter, the encoding-decoding-based recursive filtering problem has been addressed for a class of fractional-order systems. The dynamic-quantization-based EDM has been introduced into the wireless communication network to encrypt the measurement data. A quantization error has been introduced to characterize the relationship between the decoded output and the real measurement,and the exact variance of the introduced quantization error has been calculated. By solving two Riccati difference equations and appropriately designing the filter gain, a minimum upper bound on the FEC has been attained. Finally, the effectiveness of the proposed filtering algorithm has been verified by a simulation example.
Acknowledgments: This work was supported in part by the National Natural Science Foundation of China (U21A2019, 61873058,61933007, 62103095), the Hainan Province Science and Technology Special Fund (ZDYF2022SHFZ105), the Natural Science Foundation of Heilongjiang Province of China (LH2021F005), and the Alexander von Humboldt Foundation of Germany.
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Exponential Continuous Non-Parametric Neural Identifier With Predefined Convergence Velocity
- Exploring Image Generation for UAV Change Detection
- Wearable Robots for Human Underwater Movement Ability Enhancement: A Survey
- A Scalable Adaptive Approach to Multi-Vehicle Formation Control with Obstacle Avoidance
- Fuzzy Set-Membership Filtering for Discrete-Time Nonlinear Systems
- Distributed Fault-Tolerant Consensus Tracking of Multi-Agent Systems Under Cyber-Attacks
