Exponential Continuous Non-Parametric Neural Identifier With Predefined Convergence Velocity
2022-06-25MarianaBallesterosRitaFuentesAguilarandIsaacChairez
Mariana Ballesteros, Rita Q. Fuentes-Aguilar, and Isaac Chairez
Abstract—This paper addresses the design of an exponential function-based learning law for artificial neural networks (ANNs)with continuous dynamics. The ANN structure is used to obtain a non-parametric model of systems with uncertainties, which are described by a set of nonlinear ordinary differential equations.Two novel adaptive algorithms with predefined exponential convergence rate adjust the weights of the ANN. The first algorithm includes an adaptive gain depending on the identification error which accelerated the convergence of the weights and promotes a faster convergence between the states of the uncertain system and the trajectories of the neural identifier.The second approach uses a time-dependent sigmoidal gain that forces the convergence of the identification error to an invariant set characterized by an ellipsoid. The generalized volume of this ellipsoid depends on the upper bounds of uncertainties,perturbations and modeling errors. The application of the invariant ellipsoid method yields to obtain an algorithm to reduce the volume of the convergence region for the identification error.Both adaptive algorithms are derived from the application of a non-standard exponential dependent function and an associated controlled Lyapunov function. Numerical examples demonstrate the improvements enforced by the algorithms introduced in this study by comparing the convergence settings concerning classical schemes with non-exponential continuous learning methods. The proposed identifiers overcome the results of the classical identifier achieving a faster convergence to an invariant set of smaller dimensions.
I. INTRODUCTION
NON-PARAMETRIC identification represents a key tool to develop adaptive control for uncertain systems. Some of these identifiers apply approximation theory to obtain a useful model of a system with uncertainties [1]. If the model could represent the input-output relationship with enough(according to the designer) accuracy, then, this model can be used to design disturbance canceling feedback controllers [2].
Usually, the approximate model considers a linear combination of either states or functions, which formed a basis in a specific Hilbert space. The non-parametric approximation strategy individualizes the model by adjusting theweights(linear parameters) of each component (state or functions) in the basis [3]. In consequence, most of these identifiers use different variations of the least mean square method (LMS) to obtain the specific model that fits better (in terms of the norm used to define the performance index to be minimized by the LMS) with the input-output relationship [4], [5].
Few results consider a nonlinear dependence of the weights characterizing the uncertain model. The selection of functions to form the basis establishes a particular form of the approximate model. In the context of this study, the basis is composed of sigmoid functions yielding to the concept of a non-parametric neural identifier [6], [7]. Neural identifiers use the approximation properties of artificial neural networks(ANNs) [8]-[11]. The specific form of sigmoid functions satisfies the definition introduced by Cybenko [12]. Then,Logistic, S-shaped, or inverse tangent can be feasible selections of the elements forming the basis.
Over the past decades, the notion of neural identifier has solved the problem of designing approximate models for diverse systems using a simplified one-layer (output-layer)structure [13]. Many other identifiers used adaptive theory to obtain the estimation of the weights, even in more complex topological forms with multiple layers. Notice that, most of these identifiers were not able to predefine the convergence velocity of identification error and they only can ensure the upper bound of the convergence region for the trajectories of the identification error.
The potential application of a neural identifier within the design of the adaptive controller demands thefastest possibleconvergence of the identification error. This vague concept can be reinterpreted in terms of the prescribed performance idea proposed in [14]-[16]. The prescribed performance idea considers that the tracking error should converge to an arbitrarily small residual set with convergence rate greater or equal than a pre-specified value. In literature, prescribed performance usually introduced a nonlinear transformation that converts the original design into a stabilization problem that can be solved by proposing a suitable Lyapunov function candidate. The nonlinear transformation considers the application of an exponential function that appears hidden in the design of the approximate model based on ANNs.
The idea of storing past information of states in the uncertain system serves to design the concurrent learning solution, which leads to prescribed exponential bounds for the identification error [17], [18]. Nevertheless, the continuously growing storage of past states limits the application of such class of solutions. The velocity gradient method is another remarkable variant of the methods developed to fix the convergence velocity [19]. Different variants of LMS solutions to estimate the weights have been studied recently with interesting results, but still providing an ex-post characterization of the exponentially convergence bounds. An example of the design of adaptive controllers where the estimated weights used on the identifier structure yielding a compensating structure and a linear correction element on the tracking error using Barrier Lyapunov functions is presented in [20]. A different option to enforce a prescribed performance for the modeling process using ANNs is based on the socalled control Lyapunov function (CLF). These functions have been considered a keystone element in the design of feedback controllers. In the context of non-parametric modeling, CLFs are central elements to design different weights estimation rules that provide diverse characteristics to the stability of the origin in the space of the identification error. In contrast to the classical CLF where the control design is the main objective,the application of such class of CLF in non-parametric modeling yields to define learning laws that can force prescribed transient behavior.
This study proposes two particular forms of CLF that have exponential associated functions modifying the transient performance for the identification error. The main novelties and contributions of this work are:
1) We use a CLF to design the learning laws in the neural identifiers with the peculiarity of adding exponential elements to enhance the convergence of the identification error. This exponential control Lyapunov function (ECLF) is conformed by the classical quadratic elements and an additional exponential structure depending on either the identification error or a pure time depending variable.
2) The motivation for using ECLF arises from other identification and control fields as time delay control theory or optimal control [21]-[23], where such a class of functions is used in performance indexes with a discount. Indeed, the application of ECLF provides faster convergence of the states to the equilibrium point when the optimal solution is applied as a stabilizing controller [24]. This study presents a contribution to adaptation by including the ECLF in the design of adaptive weights.
3) We present two ECLFs for the design of adaptive laws for the developed exponential identifier, the first exponential element depends on the identification error, and the second uses a time-dependent sigmoidal function that grows with predefined velocity.
4) The two variants of exponential learning laws justify a predefined transient performance for both algorithms developed in this study.
The paper is organized as follows: In Section II, notation and useful mathematical preliminaries are described. Section III defines the class of uncertain systems and the approximation properties of the ANN with continuous dynamic used in this study. Section IV describes the first identifier as well as the exponential convergent learning laws, and in the last subsection, the design of the second identifier based on a time-dependent gain for the adjustment of the weights is described. In Section V, the use of the invariant ellipsoid method to minimize the convergence region of the identification error is described. Section VI describes the numerical results used to demonstrate the benefits achieved by the methods introduced in this paper. Finally, Section VII concludes the paper with some remarks.
II. PRELIMINARIES
In this section, the notation used through the paper is defined and some important concepts for the design of the identifiers are explained.
A. Notation

B. Mathematical Background
Comparison functions are useful tools for the analysis of the stability and boundedness of control systems. In this work, the design of the neural identifier and the analysis of the identification error use this class of functions. The definitions for these functions are
Definition 1:Comparison functions:

Prescribed performance has been considered within the robust and adaptive control theories. Usually, prescribed performance used an auxiliary performance function that formalizes it in terms of generalized states such as the tracking error. In this study, the same auxiliary is also considered, but it uses the trajectories of identification error as the characterizing states.

III. UNCERTAIN NONLINEAR SYSTEMS
The class of nonlinear systems with uncertain structure satisfies the following mathematical description:


A. Neural Network Representation of the Uncertain System



IV. EXPONENTIAL NEURAL IDENTIFIER

The structure of the neural identifier can be presented in a general form as sigmoid multipliers. The second part defines the vector field associated with the control action using the second set of adaptive parametersW2(t). Indeed, the structure of the neural identifier is
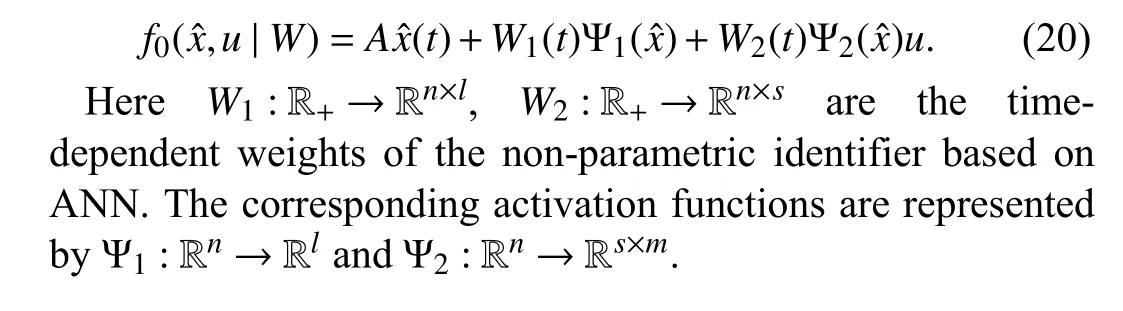
A. Problem Statement



C. Identifier With Predefined Velocity of Convergence
The structure of the neural identifier with predefined velocity considers the same general form of (19)


V. ANALYSIS OF THE CONVERGENCE REGION AND VELOCITY
This section analyzes the effect of introducing the exponential dependent functions on the DNN identifier design.
A. Identifier 1
Considering the inclusion (33) and the result of Theorem 4,the following differential inclusion is valid:

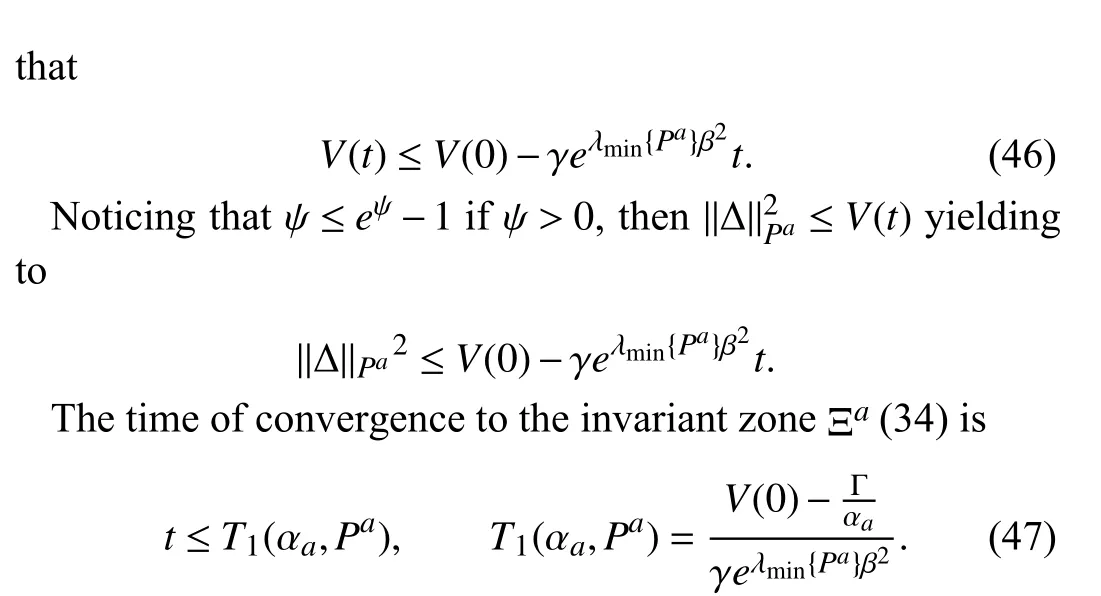
Notice that the right hand-side of (47) is a nonlinear function of the matrixPaand the positive parameter αawhich are intemately related by the solution of the bilinear matrix inequality (25). This nonlinear relation can be optimized (if such optimal solution exists with the aim of minimizing the guaranteed convergence time). Guaranteed parameter estimation is considered as an efficient tool for designing controllers, observers and parameter identifiers, including their convergence time. This approach offers remarkable advantages such as the need to know only the lower and upper bounds for the uncertain section of the system. However, the computational cost and the conservatism of the resulting estimates are two major inconveniences of this method.Guaranteed estimation method has been improved using the invariant (attractive) ellipsoid method if the uncertainties and perturbations fulfil a quadratic ellipsoidal constraint. In this paper, this condition is considered in the set of assumptions including at the beginning of this study. It is usual that parameters estimation based on the ellipsoid technique is obtained by a recurrent algorithm that estimates the intersection of ellipses. However, recent research works have brought another possible solution that is going to be used in this study. This problem can be formally stated as the following minimization problem:


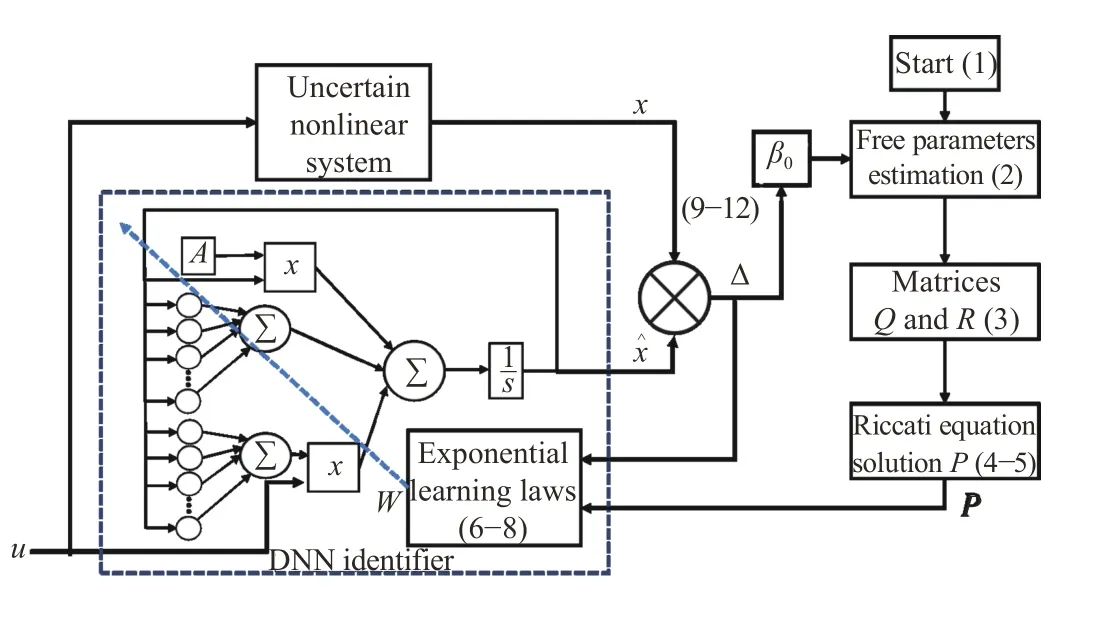
Fig. 1. Diagram of the implementation for both identifiers.
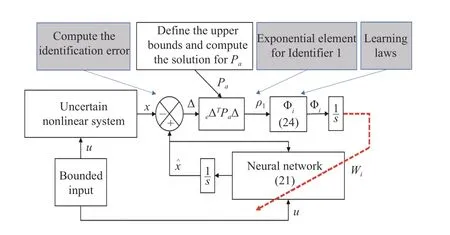
Fig. 2. Diagram of the implementation for Identifier 1.
B. Identifier 2
Considering the inclusion (42) and the result of Theorem 5,the following differential inclusion is valid:

Fig. 1 depicts a diagram with the stages to implement the proposed DNN identifiers.
Algorithm 1 describes the learning procedure, as well as how the identifier is proposed. The numbers in parentheses in Fig. 1, represent the steps from Algorithm 1.
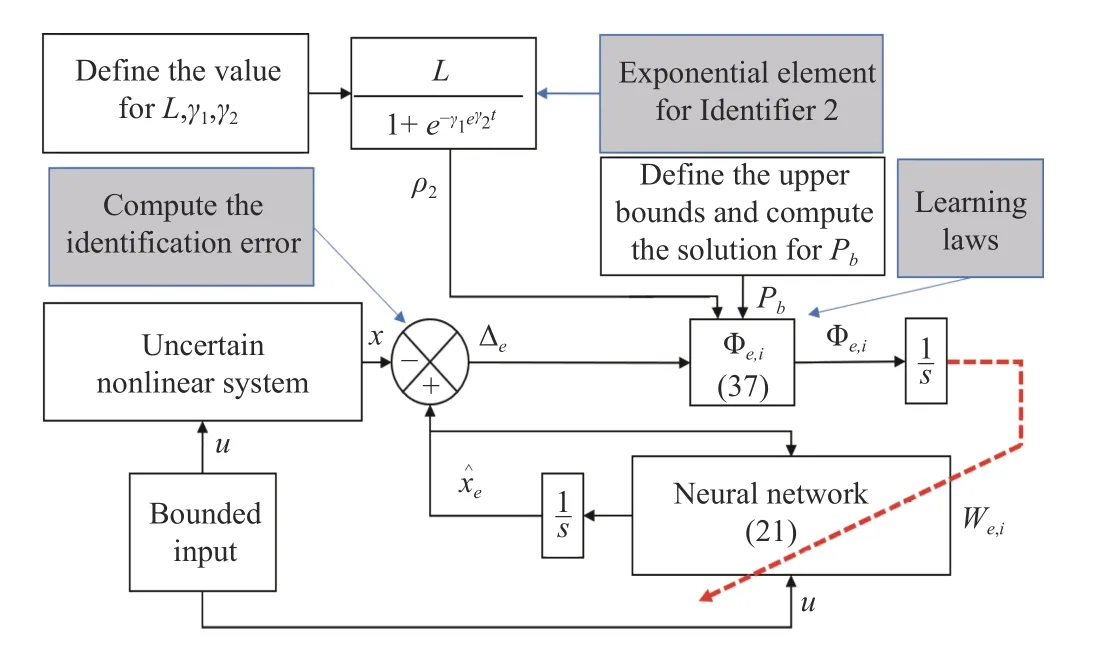
Fig. 3. Diagram of the implementation for Identifier 2.
Figs. 2 and 3 are a graphical representation of each algorithm, respectively. In both figures, the computation of the exponential element for each identifier is represented.Notice that the main difference in the design relay on the exponential. In Fig. 2, the function consists of the exponential term dependent on the identification error, while Fig. 3 depicts how the time-dependent exponential element is included in a sigmoidal. The steps and parameters needed for the implementation are shown in these figures.

Algorithm 1: Identifier Implementation 1: Start 2. Estimate the upper values for the fixed weights and ,that is and ,3: Define the values for matrices R and Q that are part of the Riccati equation 4: Implement the computational method to get the positive definite solution P of the Ricatti equation 5: If the solution of the Riccati equation exists, then:W0,1 W0,2 W+0,1 W+0,2

6: Implement the ordinary differential equation corresponding to the RDNN identifier to get the dynamic evolution of with the exponential modification 7: Implement the matrix differential equations for the three weights forming the dynamic structure of the proposed RDNN W1, and W2 8: Fix the initial values for the states of the identifier as well as for the weights W1, and W2 9: Evaluate the numerical performance of the identifier comparing the evolution of its states in comparison to the actual trajectories of the system with uncertain dynamics with uncertain model, with the estimation of the root mean square of the identification error.10: If the root mean square of the identification error is smaller than the predefined quality indicator β0, then the algorithm is finished.11: Else Modify the initial weights of the RDNN taking the final value of matrices W1, and W2 from the numerical evaluation. Then,restart the numerical evaluation with the initial weights and evaluate the root mean square value.12: Repeat this procedure until the convergence quality estimation is gotten.ˆx?
VI. NUMERICAL RESULTS
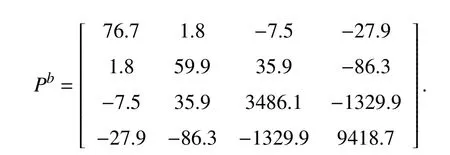
The proposed identifiers were tested on a virtual model of a robot manipulator with two degrees of freedom. The model was obtained using the Simescape MultibodyTMtoolbox of Matlab®. The dynamics is assumed uncertain but, due to the well-known characteristics of the robot modeling [35], the model satisfies all the assumptions presented in Section III, as well as the structure of the class of systems considered in this paper. Notice that for this testing, the model served as a data generator and no information from the model was considered in the identifiers design. Some parameters used in simulations are shown in Table I while the rest are in matrix form presented in this section.

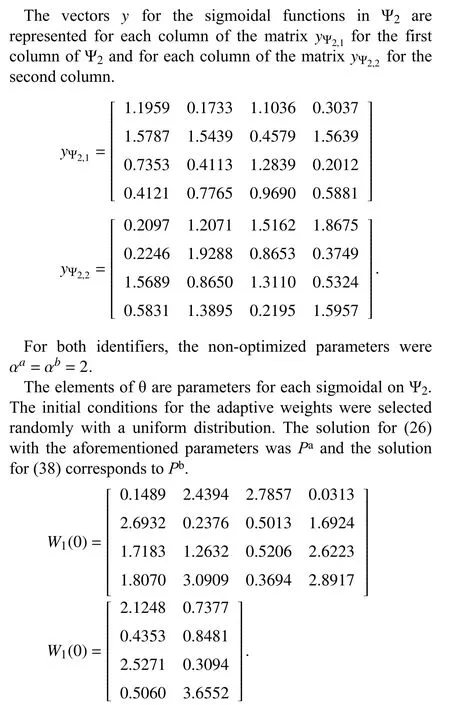
All the initial conditions, the number of neurons and the free-parameters were selected equally for the three identifiers.For the second proposed identifier γ1=1, γ2=2 andL=5.
As it can be noticed, most of the parameters were selected considering the calculus of the matrix inequality proposed in(26), estimating the upper values for the weights using the trial and evaluating procedure. This procedure leads to obtaining the value of the matrixP. The only free parameters in the learning laws were matricesK1andK2. The initial conditions for the weights and the identifier were selected randomly with a uniform distribution. The parameters considered in the activation functions for the identifier were taken from the reference [5]. The foundation principles of artificial neural network design claim that these parameters in the sigmoidal functions can be selected randomly if the number of activation functions is high enough.

and the solution for (37) corresponds to
Figs. 4-7 depict the identification result for each state of the planar manipulator of two degrees of freedom. Each figure shows the comparison between the evolution of the state for both identifiers, the state of the simulated system and a Classical DNN identifier.
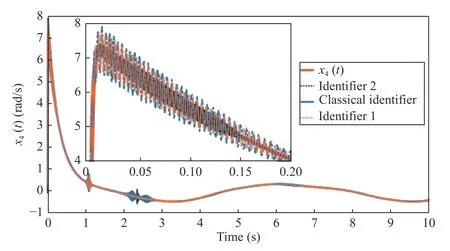
Fig. 7. Comparison of the identification results for the fourth state (angular velocity of the second link) using both of the proposed identifiers and a classical DNN identifier.
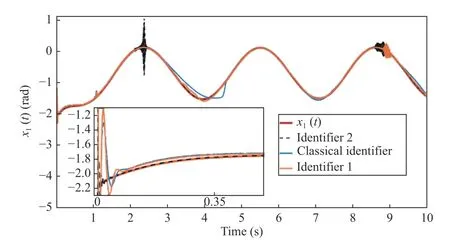
Fig. 4. Comparison of the identification results for the first state (angular position of the first link) using both of the proposed identifiers and a classical DNN identifier.
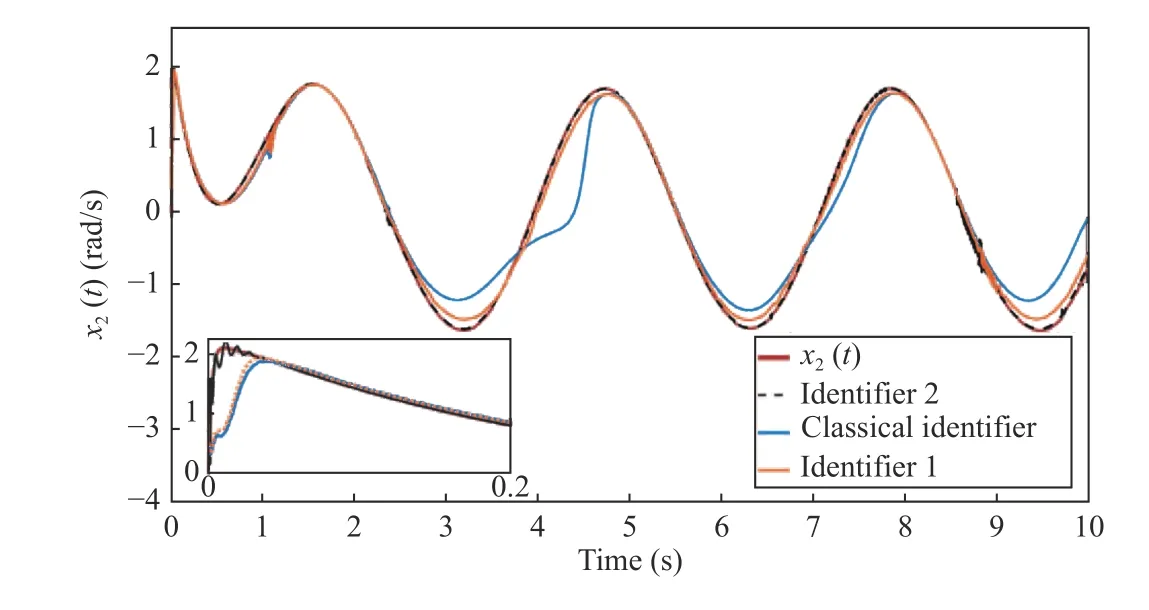
Fig. 5. Comparison of the identification results for the second state (angular velocity of the first link) using both of the proposed identifiers and a classical DNN identifier.
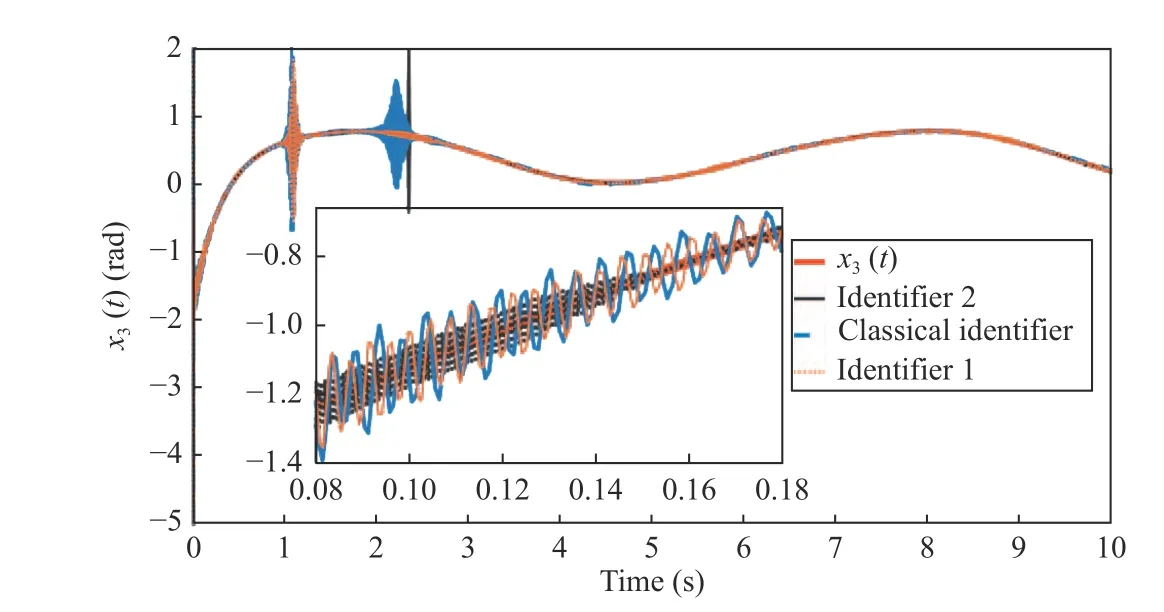
Fig. 6. Comparison of the identification results for the third state (angular position of the second link) using both of the proposed identifiers and a classical DNN identifier.
In Fig. 4, it can be appreciated how the second identifier converges faster to the system trajectory of the first state. This identifier converges in less than 0.1 seconds. In the zoomed view, the detail depicts the convergence of the classical identifier and the first proposed identifier. Notice here that the first identifier converges faster and presents oscillations of larger amplitude before 0.1 seconds. For this state, the classical identifier presents oscillations of smaller amplitude.However, the convergence to the actual state of the uncertain system was better for both proposed identifiers in this study.
The convergence of the second state of the manipulator system for the classical and the proposed identifiers is showed in Fig. 5. In this figure, one may notice the difference between the convergence of both identifiers and the classical DNN identifier (depicted with the continued blue line). In the detailed view for the first seconds, it is appreciated the fastest convergence of the second identifier (compared to the classical one) before 0.1 seconds, then the first identifier convergences and the classical identifier is the last to converge.
Fig. 6 shows the result for the convergence of the considered identifiers for the third state. In this case, the classical identifier presents oscillations of larger amplitude(comparatively). In the detailed view, the second identifier has smaller amplitude and high-frequency oscillations and converges faster (before 0.16 seconds). The first proposed identifier converges faster than the classical identifier to the position of the second link.
Similar to the previous figures, in Fig. 7, the results for the identification in the fourth state are shown. These results confirm that the classical DNN identifier presents oscillations with larger amplitudes than the proposed identifiers. In the detailed view, it is shown the fastest convergence (before 0.15 seconds) of the first proposed identifier (black line).
In Fig. 8, the comparison of the three mean square errors for the Classical identifier, First and Second proposed identifiers are depicted. In this figure, the norm for the identification error using the classical identifier has bigger oscillations and a slower convergence. This analysis justifies the design of the proposed identifiers and provides a substantial basis for the inclusion of the time varying exponential functions in the learning design.
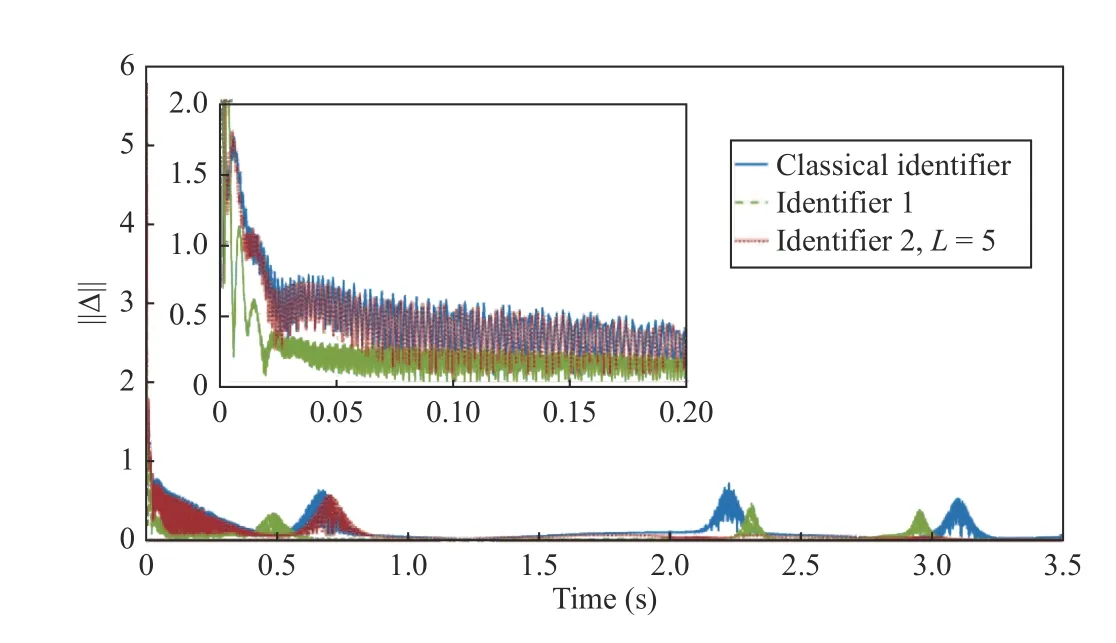
Fig. 8. Norm of the identification error using a Classical DNN identifier and the proposed DNN identifiers.
For the second identifier, Fig. 9 shows a comparison of the norm for the identification error using different values forL,the red line depicts the result for anL=5 and the blue dotted line for anL=20. This comparison using different values shows the relation of the parameterLin the velocity of convergence. Moreover, this comparative result emphasizes the possibility of fixing the convergence characteristics for the designed identifier with the learning laws presented in (36).
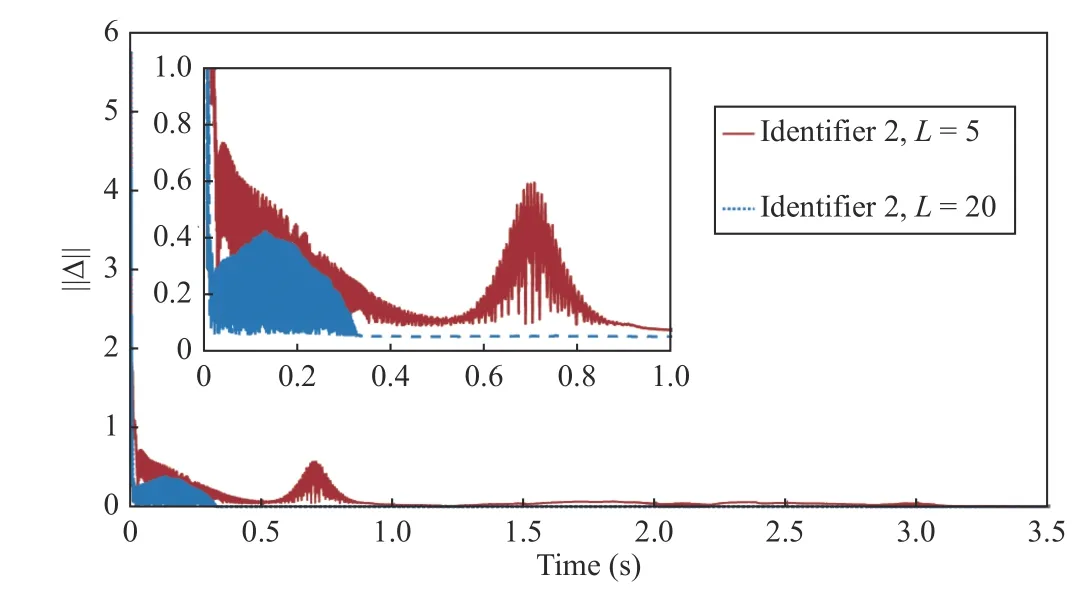
Fig. 9. Norm of the identification error. Comparison between the results of the second proposed identifier selecting different values for the L parameter.
As it has been revised, the proposed ECLF provides a transient constraint for the trajectories of the identification error. This fact appears as a significant improvement over the traditional CLF which is not able to regulate the converged velocity for the identification error.
VII. CONCLUSION
This paper discussed the design of the learning laws for an ANN structure devoted to system identification. The design included the addition of exponential functions in the Control Lyapunov function. The exponential functions were selected considering the concept of performance functions or prescribed performance. The Lyapunov analysis for the convergence of the identification error and the weights error was developed and the ultimate bound of the proposed designs was obtained. The analysis gave an estimation of the time of convergence to the invariant set around the origin using the exponential functions. For the second design one of the free parameters,Lcan be used to obtain a prescribed-like performance or improve the velocity of convergence. In the first identifier, the parameters of the identifier affect both, the size of the zone of convergence around the origin and the velocity of convergence. This study introduced a methodology to regulate the convergence velocity of the identification error enforced by the class of DNN proposed here. This accelerated convergence could be used to design hyper-exponential convergence for the identification error, uniform convergent identifier as well as the design of identifiers for delay systems with exponential convergence. Notice that all the improved characteristics of the exponential convergent identifier can be exploited in the design of adaptive controllers using the approximated model based on DNN.
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Exploring Image Generation for UAV Change Detection
- Wearable Robots for Human Underwater Movement Ability Enhancement: A Survey
- A Scalable Adaptive Approach to Multi-Vehicle Formation Control with Obstacle Avoidance
- Fuzzy Set-Membership Filtering for Discrete-Time Nonlinear Systems
- Distributed Fault-Tolerant Consensus Tracking of Multi-Agent Systems Under Cyber-Attacks
- Adaptive Control With Guaranteed Transient Behavior and Zero Steady-State Error for Systems With Time-Varying Parameters
