A Scalable Adaptive Approach to Multi-Vehicle Formation Control with Obstacle Avoidance
2022-06-25XiaohuaGeQingLongHanJunWangandXianMingZhang
Xiaohua Ge,, Qing-Long Han,, Jun Wang,, and Xian-Ming Zhang,
Abstract—This paper deals with the problem of distributed formation tracking control and obstacle avoidance of multivehicle systems (MVSs) in complex obstacle-laden environments.The MVS under consideration consists of a leader vehicle with an unknown control input and a group of follower vehicles,connected via a directed interaction topology, subject to simultaneous unknown heterogeneous nonlinearities and external disturbances. The central aim is to achieve effective and collisionfree formation tracking control for the nonlinear and uncertain MVS with obstacles encountered in formation maneuvering,while not demanding global information of the interaction topology. Toward this goal, a radial basis function neural network is used to model the unknown nonlinearity of vehicle dynamics in each vehicle and repulsive potentials are employed for obstacle avoidance. Furthermore, a scalable distributed adaptive formation tracking control protocol with a built-in obstacle avoidance mechanism is developed. It is proved that, with the proposed protocol, the resulting formation tracking errors are uniformly ultimately bounded and obstacle collision avoidance is guaranteed. Comprehensive simulation results are elaborated to substantiate the effectiveness and the promising collision avoidance performance of the proposed scalable adaptive formation control approach.
I. INTRODUCTION
MULTI-vehicle systems (MVSs) have found their widespread applications in both military and civilian areas, such as formation flying, target tracking, surface combat operations, border patrol and surveillance, intelligent transportation, coastal environmental monitoring and mapping. A key feature of such MVSs lies in that multiple autonomous vehicles, which can be extensively deployed on the ground, in the air, at sea, and underwater, cooperate with each other through some networked medium so as to fulfill a variety of coordinated control tasks. Among various research hotspots on MVSs, formation control that aims to steer a fleet of autonomous vehicles, via collaborative and distributed information processing, into forming a specific geometric pattern in terms of their states (e.g., position, heading) has attracted intensive attention; see, e.g., the recent surveys[1]-[4], and the references therein.
Depending on whether there is any leader, the existing results on formation control of MVSs and general multi-agent systems (MASs) can be roughly classified into three types:formation producing[5]-[10], where there is no leader involved;formation tracking[11]-[19], where is only one leader, either virtual or real, guiding a team of formable follower vehicles; andformation-containment[20]-[23],where a team of follower vehicles is to navigate into a convex hull formed by another team of formable leader vehicles.Several approaches are reported to analyze the MVS formation behaviors and design various formation control strategies [1]-[4].
The completion and performance of coordinated control tasks for MVSs are significantly affected by nonlinearities,and their effects become particularly adverse for small vehicles due to their low inertia and small size. For example,the navigation and control of unmanned aerial vehicles can be substantially affected by uncontrolled nonlinearities including wind gusts and gravity gradients. In addition, autonomous surface and underwater vehicles usually suffer from environmental influences induced by turbulent ocean waves and currents. In this sense, some existing formation control strategies dedicated to known or linear dynamical vehicle/agent models (e.g., [5]-[8], [10], [11], [13], [16]) may no longer be applicable. Therefore, the first challenge for nonlinear MVS formation control is to deal with the unknown nonlinearities in vehicle dynamics. On the other hand,practical formation maneuvers of a team of mobile vehicles are often implemented in some unknown and obstacle-laden environments without anya priorimap knowledge. In such a scenario, there is a strong need for a safety guarantee of collision avoidance for the vehicles in some cluttered environments while maintaining task completion of the formable vehicle team. More specifically, an effective obstacle avoidance strategy is essential to be embedded in the desired formation control protocols and algorithms. However,how to realize the intrinsic collision-free formation control of MVSs in an obstacle-laden setting remains a challenge due to its complexity in analysis and design procedures [14].
Neural networks (NNs) have been well exploited for modeling complex dynamic systems due to their great potential for identifying the unknown nonlinearities and/or uncertainties in system dynamics. For example, robust distributed adaptive NN controllers are designed for cooperative tracking control of higher-order nonlinear MASs with a nonautonomous dynamic leader [24]. Distributed NN synchronization controllers are proposed for solving the leader-follower synchronization problem of uncertain nonlinear dynamical MASs [25]. Event-based distributed cooperative NN learning control strategies are presented for different nonlinear MASs [26], [27]. Based on adaptive NN and prescribed performance control, the problem of distributed cooperative compound tracking of a platoon of vehicles of nonlinear third-order dynamics is resolved in finite time [28]. For a class of nonlinear MASs in a nonstrict feedback form, a finite-time adaptive NN fault-tolerant control method is developed to tackle actuator faults, unknown symmetric output dead zones and control coefficients [29]. An adaptive NN leader-following tracking method is proposed for a class of fractional-order MASs with unknown matched uncertainties [30].
In order to ensure the safe mission completion of MASs,several obstacle and collision avoidance methods are available in the literature. For example, building on the concept of barrier certificates, a control barrier function-based method[31], [32] is adopted to preserve collision-free formation behaviors in MASs. Nevertheless, each agent typically relies on a formally designed nominal controller together with a tailored collision avoidance controller to make agents swap behaviors between formation maneuvers and collision avoidance navigation. Viewing the collision avoidance conditions as some design constraints, a model predictive control method [33], [34] is also employed to accomplish collision-free formation control. However, such a method may lead to some high-dimensional nonconvex and nonlinear optimization problems that are difficult to solve. On the other hand, an artificial potential field (APF) method [35] is intensively explored in the multi-vehicle (robotics) control literature. The rationale behind such a method is that an obstacle is treated as a high-potential point and a suitable repulsive potential is constructed for keeping each vehicle away from the obstacle. During a maneuver, each vehicle follows the gradient of the potential and is repelled by obstacles once it moves into a predefined range around obstacles. For example, the APF method andH∞analysis are combined to cope with the formation tracking and obstacle avoidance of a class of stochastic second-order MASs [14].Based on virtual and behavioral structures, the formation control of a team of mobile robots is studied [36], where rotational potential field is applied for obstacle avoidance of robot swarming and regular polygon formations. For linear and deterministic second-order MASs, a potential functionbased formation tracking algorithm is proposed [37] to deal with communication constraints among agents, and a timevarying formation tracking control protocol based on an improved distance- and velocity-dependent potential function[38] is developed to ensure collision avoidance among agents.Interested readers are referred to the survey [39] for more results on collision avoidance. To the best of the authors’knowledge, for MVSs with unknown nonlinearities and uncertainties, how to develop an effective formation control approach to both desired formation tracking and assured obstacle avoidance in obstacle-laden environments has not been adequately addressed hitherto, which motivates this study.
In this paper, we address the adaptive and collision-free formation tracking issue of MVSs maneuvered in an unknown and cluttered setting. In contrast to some existing formation control frameworks which assume that vehicle (or agent)dynamics are either free of any nonlinearity or perturbation, or are subject to nonlinearity and disturbance with explicitly known bounds, a general framework of time-varying formation tracking control is established to account for simultaneous unknown heterogeneous nonlinearities and external disturbances in every follower vehicle dynamics and also unknown nonzero control input in the leader. The novelty of this paper lies in the development of a scalable adaptive formation control approach to MVSs over a directed interaction topology, which achieves simultaneous formation tracking and obstacle avoidance guarantees under unknown nonlinearities and disturbances as well as obstacles, while not relying on global information of the interaction topology of the MVS.
The main contributions of this paper are twofold. 1)A scalable adaptive formation tracking control protocolis developed such that each individual vehicle only needs the information of its underlying neighbors and itself to compute its protocol parameters. Note that the challenge of the protocol design is to guarantee that both the formation tracking control protocol and the NN parameter tuning laws adopt merely local information available at each vehicle, and do not depend on the global topology information. It makes a distinctive difference between this work and some existing formation control laws, where their formation control protocols necessitate certain global knowledge of either nonzero eigenvalue in the Laplacian or eigenvectors related to the Laplacian, and thus may not be practically implementable by every vehicle (or agent); and 2)An efficient collision avoidance mechanismis delicately embedded into the desired distributed formation control protocol in such a way as to achieve guaranteed formation maneuver safety in obstacleladen environments. Furthermore, a design algorithm is provided to detail the main steps for the design of the desired scalable adaptive formation tracking control laws, through which the protocol gain and adaptive parameters as well as the repulsive force for collision avoidance can be determined. It is proved that all controlled variables are uniformly ultimately bounded and obstacle avoidance is guaranteed for every vehicle in formation maneuvering.
The remainder of the paper is organized as follows.Preliminaries are provided in Section II. The formulation of the main problem is given in Section III. The main results with a detailed design algorithm and rigorous stability analysis on the resulting closed-loop MVS are stated in Section IV.Simulation results are discussed in Section V. Concluding remarks are made in Section VI.
II. PRELIMINARIES
A. Notations

B. Graph Theory Fundamentals

III. PROBLEM FORMULATION
A. Vehicle Dynamics



B. Vehicle Formation Geometry

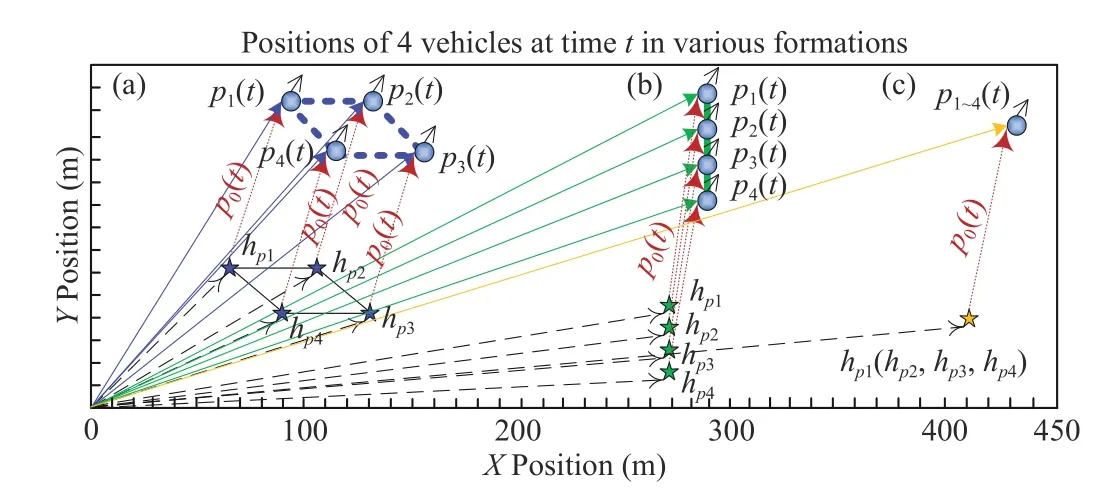
Fig. 1. Three illustrative examples of four vehicles moving in the X Y plane in various formations: (a) a parallelogram formation; (b) a straight line formation; and (c) a point formation (consensus).

C. Obstacle Avoidance Function

encounter bulky obstacles during formation maneuvering,making the entire vehicle team quite difficult, if not impossible, to pass by. To model a bulky obstacle properly, it is natural to assume that a bulky obstacle can be suitably approximated with some convex polyhedra. As a result, one can further take some critical sample points on the boundary of the polyhedra to approximate the bulky obstacle. In practice, this can be accomplished by using suitable cameras,sonars, or laser range finders on vehicles, to provide effective identification of the boundary surface of the polyhedra together with some signal and image processing techniques.Then, the obstacle avoidance functions can be derived from the surface integrals on boundary of the obstacle. Generally,more samples on the boundary of the polyhedra surely make the modeling of the bulky obstacle more explicit and accurate.Thus, the desired obstacle avoidance performance becomes apparent.

D. The Problem to Be Addressed

obstacles during formation maneuvers.
IV. MAIN RESULTS
In this section, we first specify the desired scalable adaptive formation tracking control protocol. We then present an algorithm for determining the gain parameters and NN parameter tuning rules for the desired control protocol.Finally, we derive the resulting closed-loop formation tracking error dynamics and perform a rigorous stability analysis by proving that all the closed-loop signals remain uniformly ultimately bounded and the desired formation tracking objective can be achieved with assured obstacle avoidance.
A. Scalable Adaptive Formation Tracking Control Protocol


B. Design Algorithm


C. Stability Analysis





Remark 9:The importance of the proposed scalable adaptive formation tracking control design approach is fourfold.(i)The developed Algorithm 1 for realizing distributed adaptive formation tracking control can adequately accommodate the unknown nonlinearity and external disturbance in follower dynamics as well as the unknown nonzero control input in the leader dynamics in a unified framework. This is contrast to some existing formation control approaches [5]-[8], [10], [11], [13], [16], [17] which assume that the vehicle (or agent) dynamics are free of any nonlinearity or external perturbation.(ii)Although the bounding conditions are exposed in Assumptions 2-4, it is clearly shown in Algorithm 1 that the bounds of the unknown disturbancewi, the unknown nonzero leader control inputu0,the signals and matrices φi,εi,Wiin NNs, and the obstacle avoidance functions ψisare not required to be knowna priorifor the design of desired distributed adaptive formation tracking protocols. It represents a clear difference from some existing results such as [12], [14] where the design criteria or algorithms necessitate the information of relevant bounds.(iii)Further to the discussion in Remark 4, the proposed design algorithm can be tailored to deal with several important cooperative control issues in MVSs/MASs, such as bounded(practical) leaderless consensus, leader-following consensus,and target enclosing and pursuing.(iv)In contrast to some existing formation (tracking) control approaches which require some global knowledge of either the nonzero eigenvalues in the Laplacian [10], [11], [16] or the eigenvectors related to the Laplacian (or matrix H ) [14], [37],the proposed adaptive formation tracking protocol (11) for each vehiclei, however, relies on only the information of itself and its underlying neighbors, and thus enjoys a scalability property. Moreover, the distributed formation tracking problem herein is pursued under a directed interaction topology, which is more difficult than that under a undirected topology [5], [7], [11], [38].
V. ILLUSTRATIVE EXAMPLES
In this section, two illustrative examples are provided to demonstrate the effectiveness and merits of the proposed scalable adaptive formation control approach with guaranteed collision avoidance.
A. Multi-Vehicle Formation Tracking in An Obstacle-Laden 2D Plane


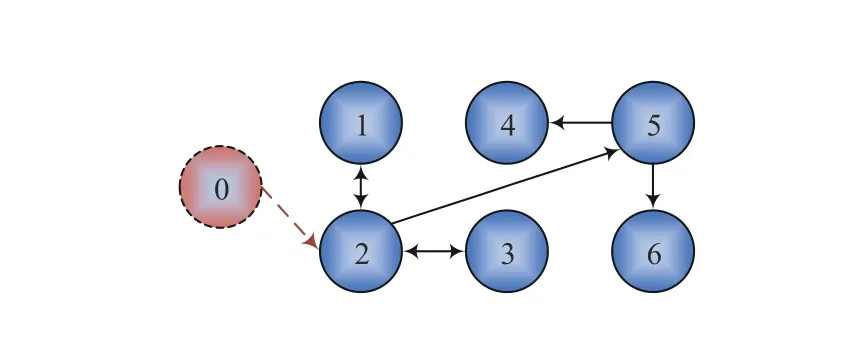
Fig. 2. Communication topology of six followers and the virtual leader 0.



Fig. 3. Formation tracking behaviors of the controlled vehicle fleet in an obstacle-laden environment: (a) The six follower vehicles eventually follow the virtual leader’s motion trajectory with the desired hexagon pattern subject to small formation tracking errors, while successfully avoiding collision with the obstacles during the formation maneuver; (b) The velocities viX(t) of the six follower vehicles in the X plane achieve bounded consensus on that of the virtual leader; (c) The velocities viY(t) of the six follower vehicles in theY plane achieve bounded consensus on that of the virtual leader; (d) Bounded control input uiX(t) in the X plane; (e) Bounded control input uiY(t) in theY plane; and (f) Adaptive coupling gains αi(t) is convergent to some steady values in finite time, i ∈V.
We then evaluate the MVS formation tracking and obstacle avoidance performance by resorting to the proposed Algorithm 1. Fig. 3 (a)-(c) illustrates that all six follower vehicles smoothly bypass all obstacles without colliding with any of them, while still being capable of successfully tracking the virtual leader with the desired hexagon formation.Moreover, Fig. 3 (d)-(f) depicts that the bounded closed-loop signals, including the control inputsuiXanduiYas well as the convergent adaptive coupling gains αi. Fig. 4 illustrates six snapshots of the resultant vehicle formation at different times.Fig. 5 depicts the nonlinearityfiand its approximationfˆifor every vehicle, wherein the nonlinear functionsfiin six follower vehicles are well estimated by the RBF NN.

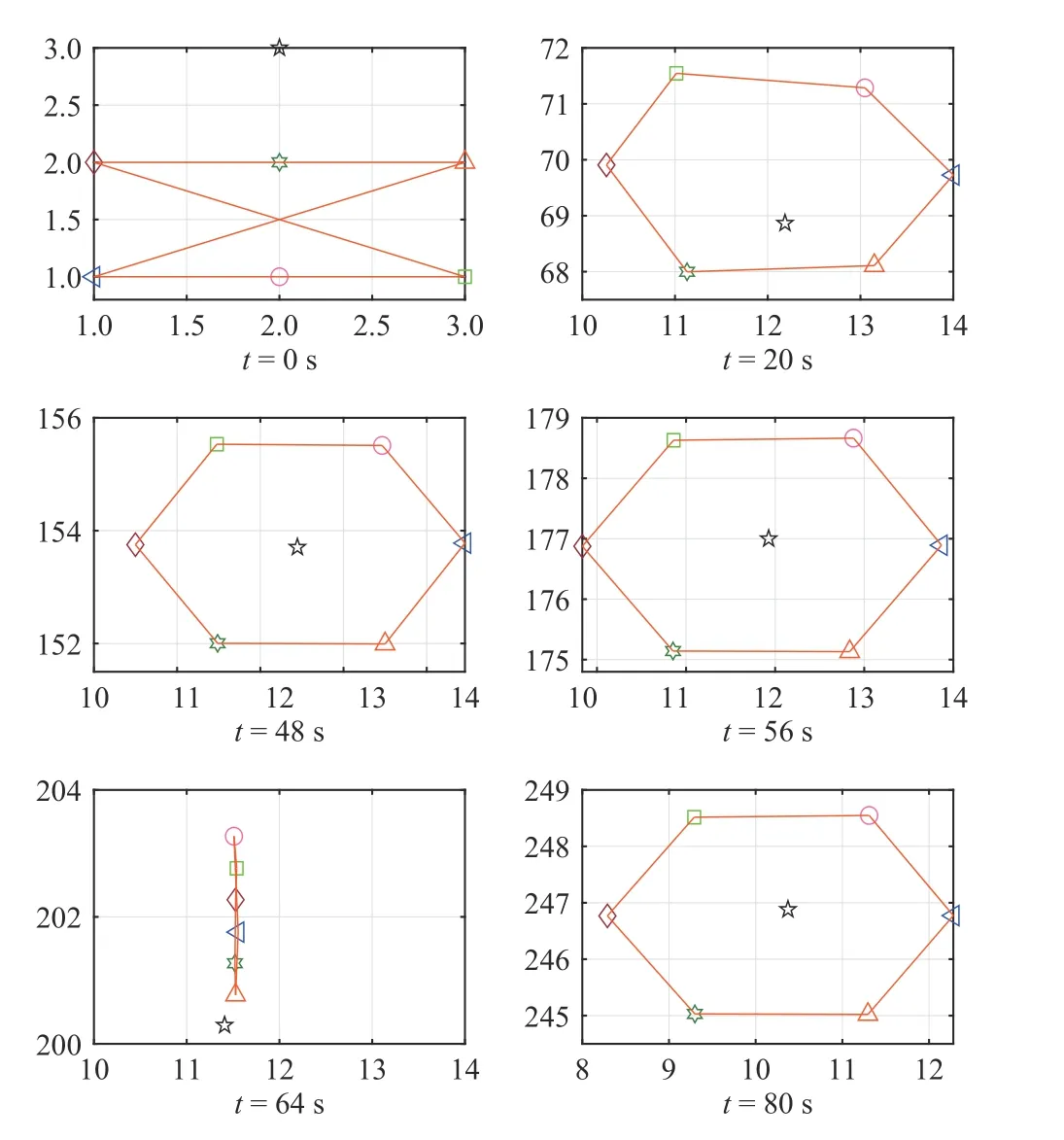
Fig. 4. Snapshots of the vehicle formation at different times of t=0 s,t=20 s, t =48 s, t =56 s, t =64 s, and t =80 s.
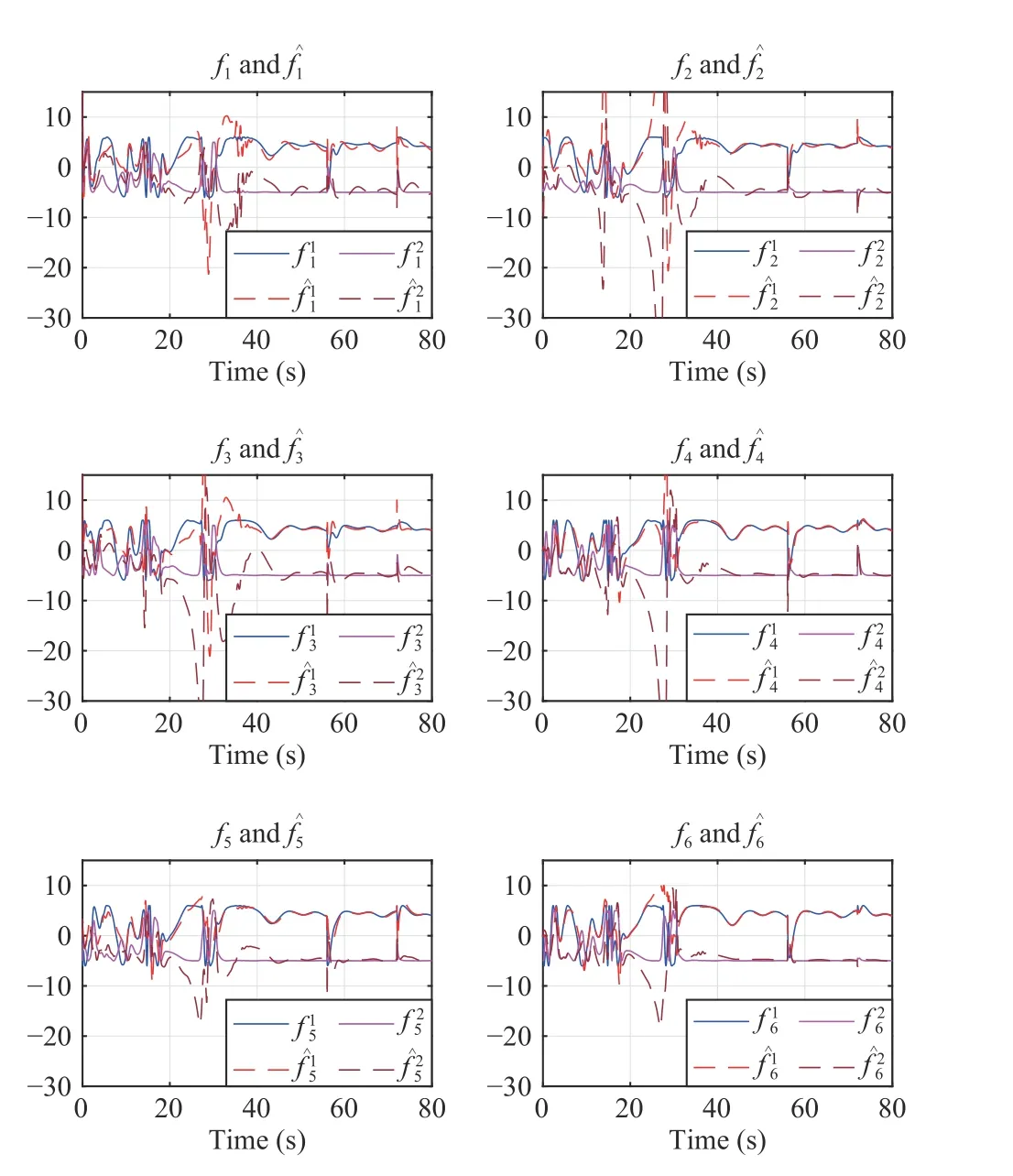
Fig. 5. NN approximation fˆi(·)=[ fˆi1 (·), fˆi2(·)]T of the nonlinear fi(·)=[fi1 (·),fi2 (·)]T for each follower vehicle, i ∈V.


In summary, the above simulation results adequately demonstrate that the proposed scalable adaptive formation tracking control approach can not only steer a fleet of follower vehicles to follow the desired virtual leader but also guarantee the obstacle avoidance during formation maneuvers in complex obstacle-laden environments.
B. Collision-Free Vehicle Platooning in A Longitudinal Plane



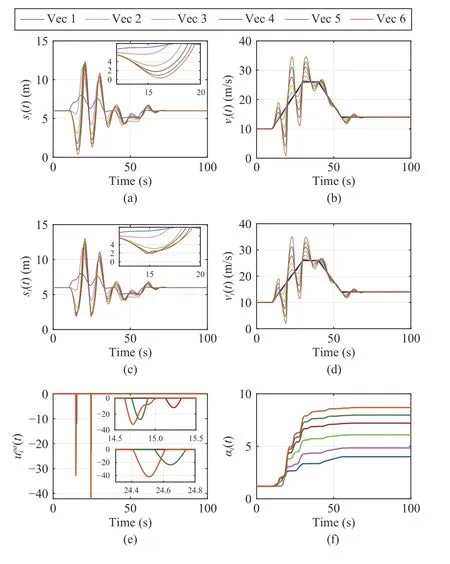
Fig. 6. Platooning and collision avoidance performance under the desired constant spacing ( si-1,i=6 m) in the presence of external disturbance input wi(t) and leader control input u0(t): (a) Inter-vehicle distancessi(t)=pi-1(t)-pi(t) between each platoon member i and its direct predecessor i-1, i ∈V,without the collision avoidance function ψ i,i-1(di,i-1(t)); (b) Vehicle velocities vi(t), i ∈V~ , without the collision avoidance function ψ i,i-1(di,i-1(t)); (c) Intervehicle distance si(t)=pi-1(t)-pi(t), i ∈V, in the presence of ψi,i-1(di,i-1(t)); (b) Vehicle velocities vi(t), i ∈V~, in the presence of ψi,i-1(di,i-1(t)); (e) Repulsive force uoi a(t), i ∈V, for collision avoidance; and(f) Adaptive coupling gains α i(t), i ∈V in the presence of ψ i,i-1(di,i-1(t)).
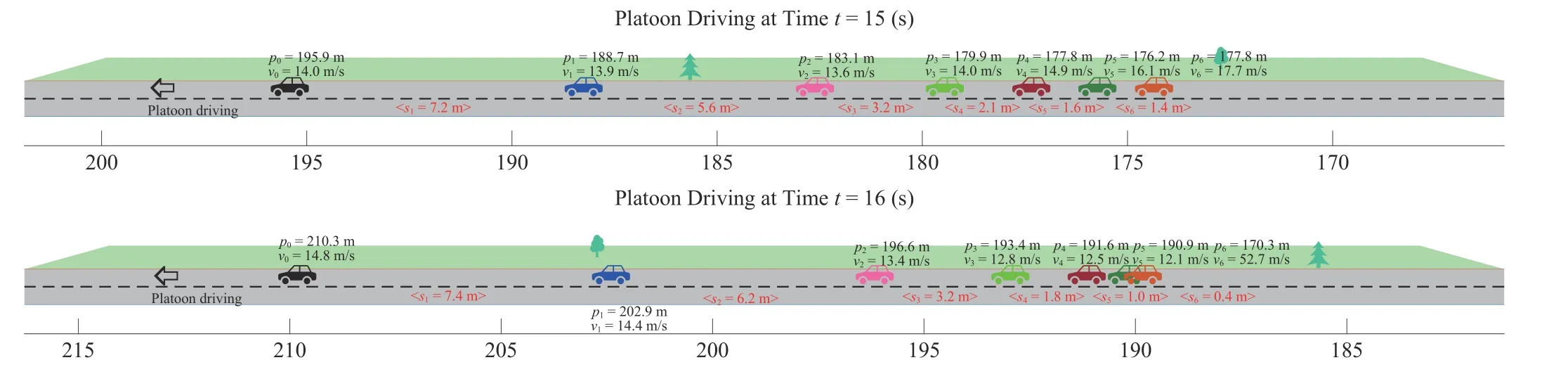
Fig. 7. Snapshots of the simulated platoon driving maneuver under the desired constant spacing (6 m) without the collision avoidance function ψ i,i-1(di,i-1(t)),where potential collisions occur among followers 4 ,5, and 6 given that s 6(t)=0.4 m and s5(t)=1.0 m at time t =16 s.

Fig. 8. Snapshots of the simulated platoon driving maneuver under the desired constant spacing (6 m) with the collision avoidance function ψi,i-1(di,i-1(t)),where the spacings among followers 4 ,5, and 6 at time t =16 s are enlarged to s 6=2.7 m and s5=2.6 m.

VI. CONCLUSIONS
The distributed adaptive formation tracking control is tackled for MVSs operating in unknown and cluttered environments. RBF NNs are used to model the unknown nonlinear dynamics of vehicles. Furthermore, repulsive potentials are introduced for vehicles to achieve collision avoidance with obstacles in the workspace. To accomplish the formation tracking task with promised obstacle avoidance, a scalable distributed adaptive formation tracking control protocol is developed without the need for any global information on the directed topology. It is theoretically proved that all signals of the resulting closed-loop dynamics are uniformly ultimately bounded. The efficacy of the proposed MVS formation control protocol and design algorithm is substantiated with the simulation results on some challenging formation maneuvers.
Notice that the proposed distributed adaptive formation tracking control approach necessitates continual data communication among interacting vehicles. This may be inapplicable in a resource-constrained communication setting.Event-triggered control has yet received intensive research interests in recent years due to its prominent advantages in maintaining desired system performance and satisfactory communication efficiency; see, e.g., the recent surveys[45]-[47]. To the best of the authors’ knowledge, it remains challenging to develop a novel event-triggered scalable adaptive formation control approach which promises both satisfactory communication efficiency and collision-free formation control performance for MVSs. This constitutes one of our future works. It would be also interesting to provide secure scalable distributed adaptive control solutions that ensure successful completion of safety-critical formation maneuvering tasks in the presence of adversarial cyber attacks.
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Exponential Continuous Non-Parametric Neural Identifier With Predefined Convergence Velocity
- Exploring Image Generation for UAV Change Detection
- Wearable Robots for Human Underwater Movement Ability Enhancement: A Survey
- Fuzzy Set-Membership Filtering for Discrete-Time Nonlinear Systems
- Distributed Fault-Tolerant Consensus Tracking of Multi-Agent Systems Under Cyber-Attacks
- Adaptive Control With Guaranteed Transient Behavior and Zero Steady-State Error for Systems With Time-Varying Parameters
