Fuzzy Set-Membership Filtering for Discrete-Time Nonlinear Systems
2022-06-25JingyangMaoXiangyuMengandDeruiDing
Jingyang Mao, Xiangyu Meng, and Derui Ding,
Abstract—In this article, the problem of state estimation is addressed for discrete-time nonlinear systems subject to additive unknown-but-bounded noises by using fuzzy set-membership filtering. First, an improved T-S fuzzy model is introduced to achieve highly accurate approximation via an affine model under each fuzzy rule. Then, compared to traditional prediction-based ones, two types of fuzzy set-membership filters are proposed to effectively improve filtering performance, where the structure of both filters consists of two parts: prediction and filtering. Under the locally Lipschitz continuous condition of membership functions, unknown membership values in the estimation error system can be treated as multiplicative noises with respect to the estimation error. Real-time recursive algorithms are given to find the minimal ellipsoid containing the true state. Finally, the proposed optimization approaches are validated via numerical simulations of a one-dimensional and a three-dimensional discrete-time nonlinear systems.
I. INTRODUCTION
MANY applications involve nonlinear systems and unwanted noises. The noise arises from inputs of the system and outputs derived with the aid of a noisy sensor.Filtering is necessary to obtain information about some quantities that are essentially internal to the system. As a result, an extensive body of theory relating to filter design has grown, such as the famous Kalman filter and its extensions[1]-[4], the H∞filter [5]-[7], and several others [8]-[10].Kalman filter is a minimum variance estimator, and theH∞filter minimizes the worst-case estimation error. The system noise, including process noise and measurement noise, is normally assumed to be statistically known in the Kalman filtering framework. Nevertheless, the bound of noises can be obtained in many practical applications, such as radar, voltage control [11], system guidance and navigation, and target tracking and attacking. This leads to set-membership filtering[12]-[14]. The idea of set-membership filtering is to give an ellipsoid centered at the state estimate containing the true state, and the size of the ellipsoidal set is subsequently minimized. A reliable localization problem was discussed in[15] for autonomous mobile robots in an unstructured environment. The need of statistical information of the noise was relaxed and linearization errors were taken into account by the proposed set-membership filter. Set-membership filtering was recently implemented in radar applications in[16] to estimate the position of an octorotor. Note that a great many applications involve linear systems, as it spurs linear set-membership filtering. However, most applications involve nonlinear systems. By comparison, nonlinear set-membership filter design is very hard, if not impossible, in many instances.For this reason, there has been a lack of attention for nonlinear set-membership filters. An attempt is made in this article to design fuzzy set-membership filter algorithms for nonlinear systems.
Due to its high-precision modeling and low-complexity computation, we first use a Takagi-Sugeno (T-S) fuzzy model to approximate the nonlinear system. T-S fuzzy modeling is based on a fuzzy partition of the state space, known as IFTHEN rules. Under each fuzzy rule, a basis system is formed.The fuzzy model is given by the aggregation of the basis systems, that is, a convex combination of the basis systems weighted by membership functions. The commonly used basis systems are linear systems [17]-[26]. However, nonlinear systems in general are hard to be approximated with high accuracy by using only the combination of linear systems. To increase the accuracy of the T-S fuzzy model, we use affine basis systems. Based on the obtained T-S fuzzy model, two fuzzy set-membership filters are constructed to find minimal ellipsoids centered at the estimated states that contain the true states. Previous works addressed the problem of setmembership filtering usingprediction-type observers [19],[27], that is,ykandxˆkare used to estimatexk+1. Our constructed filter is comprised of both prediction and filtering.The prediction step will be executed usingxˆk, the fuzzy model and the knowledge of the process noise; the filtering step involves updating the predicted value ofxk+1with measuresyk+1. Furthermore, we exploit properties of membership functions, which is critical to address the stability problem of the estimation error system. However, set-membership filtering problems in the literature usually do not include the stability analysis, as we do in this article. The problem of finding a minimal ellipsoid which contains the true system state is eventually transformed into linear objective minimization with linear matrix inequality (LMI) constraints.
The main contributions of this article are summarized as follows.
1) Under each fuzzy subspace, we utilize an affine model to achieve a more accurate approximation compared with linear models when the same fuzzy rules are applied. A complete procedure for identifying the T-S fuzzy model is given.
2) Two fuzzy set-membership filters, namely, FSMF1 and FSMF2, are proposed, where the structure of both filters consists of prediction and filtering. Compared with theprediction-type observers, the proposed filters can further reduce the state estimation error by using the most recent measurements.
3) Both the proposed filters are capable of stabilizing the estimation error system and attenuating noises, while filters in most previous studies focus on noise attenuation only. In addition, the design of FSMF2 takes full advantage of the locally Lipschitz continuous condition of the membership function, which has not been explored in previous studies. The simulation example shows a case that FSMF2 completely rejects the measurement noise for a stable nonlinear system.
The remainder of this article is structured as follows. First,the fuzzy set-membership estimation problem is formulated in Section II where the T-S fuzzy model is discussed and two fuzzy set-membership filters are designed to cater to different scenarios. Then, the filter designs are discussed to ensure that the true state is contained in an ellipsoidal set centered at the estimated state in Section III. In Section IV, a onedimensional nonlinear system and a vertical mass-spring system are given to evaluate the estimation performance of the proposed two filters. Our conclusions and discussions of future research are included in Section V. The proofs of lemmas are given in Appendices.
II. PROBLEM FORMULATION AND FILTER DESIGN
A. Nonlinear Plant


B. Fuzzy Model and Fuzzy Filter

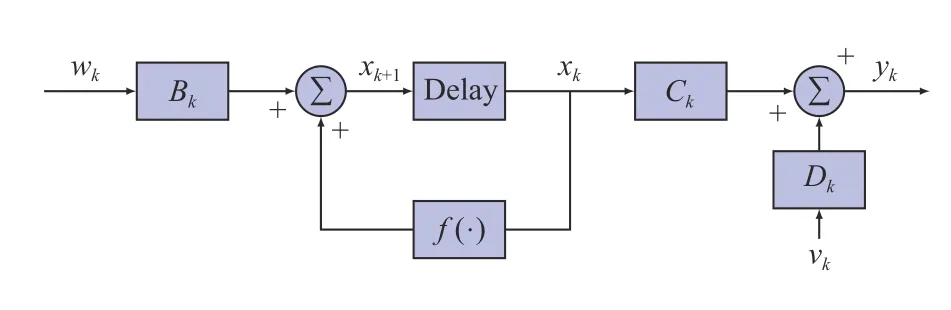
Fig. 1. Finite-dimensional nonlinear systems serving as basic signal model.

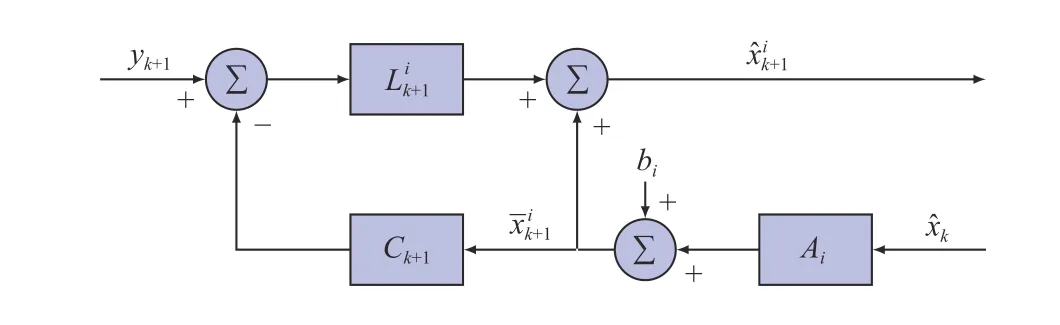
Fig. 2. Fuzzy filter under filter rule i.
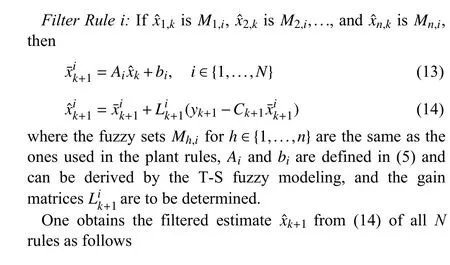

Fig. 3. Fuzzy filtering fusion.

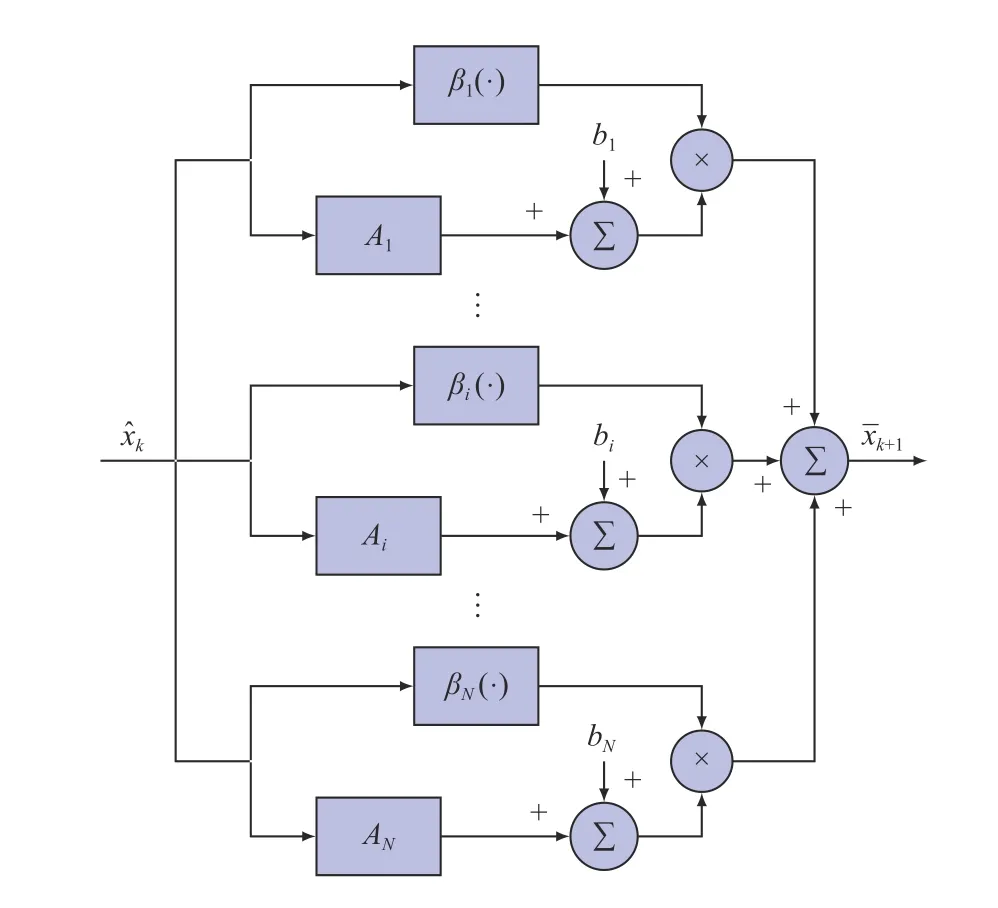
Fig. 4. Fuzzy prediction.

Fig. 5. Fuzzy filtering.

C. Objective

III. MAIN RESULTS
A. Preliminaries

B. Design of FSMF1
Define the estimation error under fuzzy ruleias
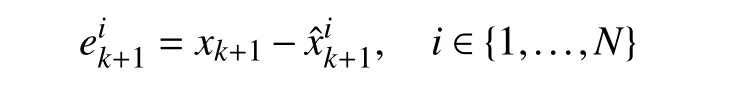



C. Design of FSMF2




IV. SIMULATION
In this section, two nonlinear systems are given to show how the proposed two filters work and to prove the validity.
A. One-dimensional Nonlinear System


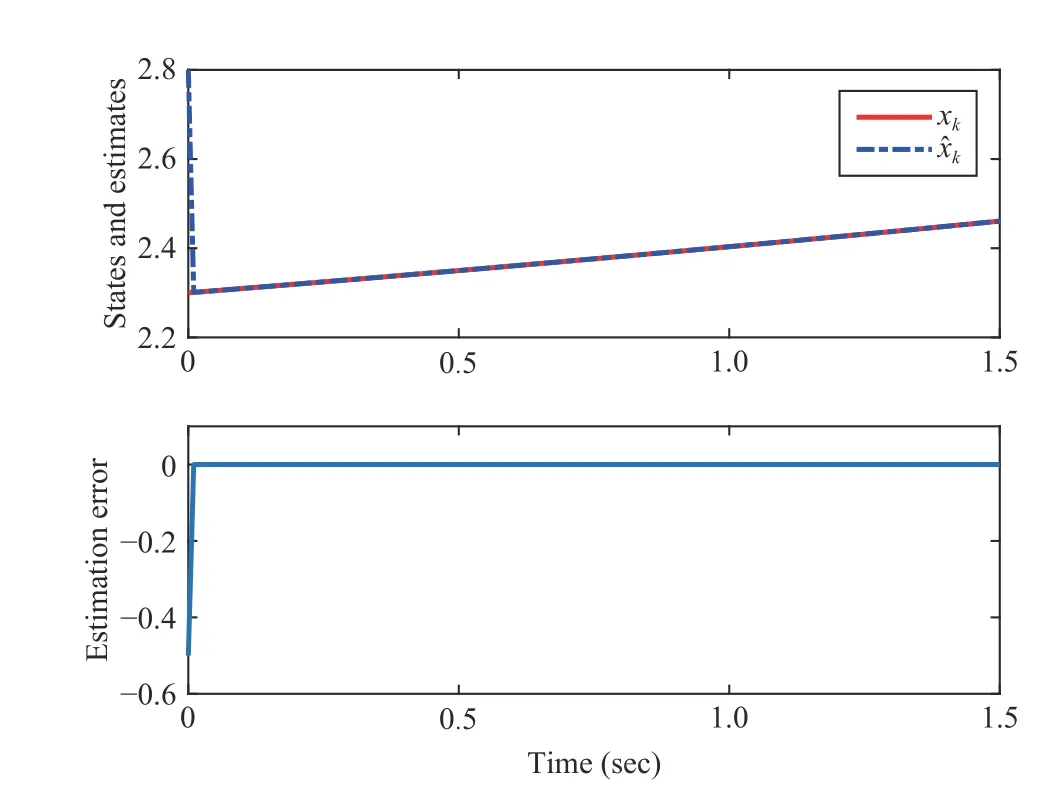
Fig. 6. System states and their estimates without noises.

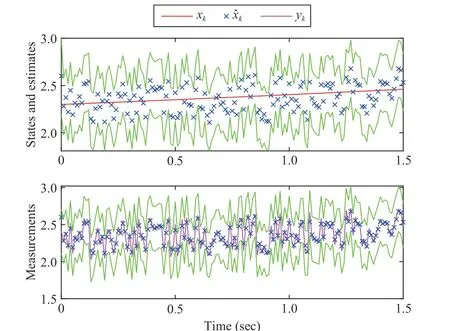
Fig. 7. Bounds of xk and yk when ρ =1 and R =0.09.

Fig. 8. Pk and e Tk P-k 1ek when ρ =1 and R =0.09.
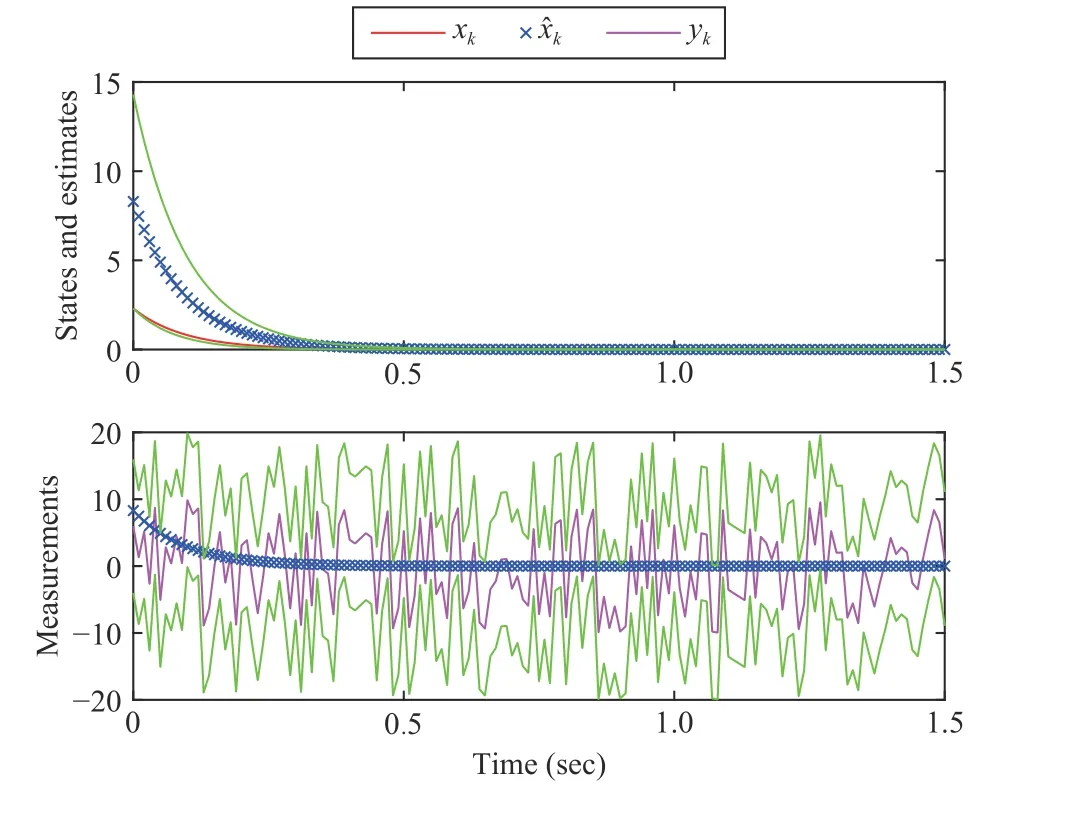
Fig. 9. Bounds of xk and yk when ρ =1 and R =100.
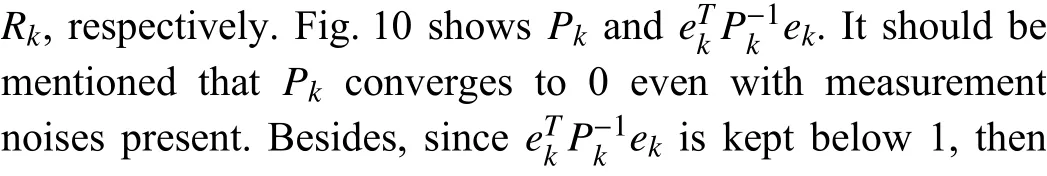
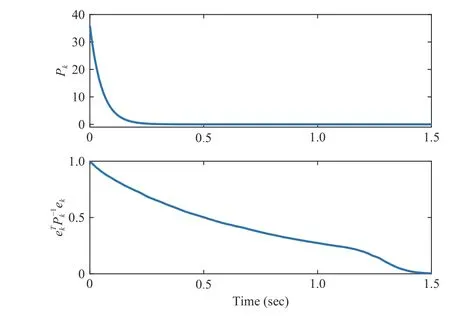
Fig. 10. P k and e Tk P-k 1ek when ρ =1 and R =100.

B. Vertical Mass-Spring System



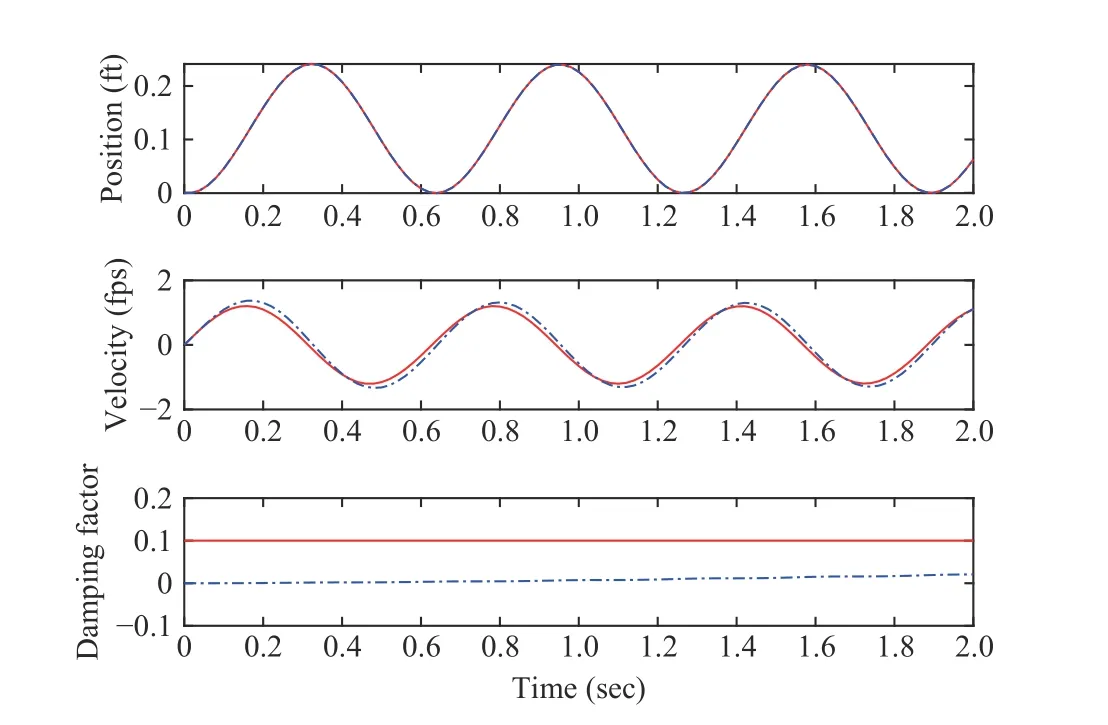
Fig. 11. System states and their estimates of the vertical spring-mass system.
In summary, both filters can be implemented online based on real-time data except the T-S fuzzy modeling, which is
Fig. 12. tr( Pk) and e Tk P-k 1ek of the vertical spring-mass system.

V. CONCLUSIONS AND FUTURE RESEARCH
In this article, the state estimation problem was studied for discrete-time nonlinear systems subject to unknown-butbounded noises. An improved T-S fuzzy model was introduced to achieve highly accurate approximation. Two fuzzy set-membership filters, namely, FSMF1 and FSMF2,were proposed that consider both the prediction and the filtering. Some features of the membership functions were utilized in the filter design so that the stability of the estimation error system can be ensured. Computational procedures were given for finding the minimal ellipsoid. Both filters can run online recursively to provide the state estimate.The methods were validated in simulation. FSMF2 showed the ability to stabilize the estimation error system and reject measurement noises.
The estimation performance is very sensitive to the parameters in the fuzzy model. Finding a satisfactory filter becomes challenging when the number of fuzzy rules increases. This is especially true when the state of the nonlinear system does not converge to zero. Possible directions for future work are the co-design of the fuzzy model and the fuzzy filter and to employ nonnegative polynomials to obtain a less conservative version of Lemma 2.In addition, we plan to extend our results to networked control systems by taking into account event-triggered communication, packet loss, etc.
APPENDIX A PROOF OF LEMMA 1


which is the same as (21).
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Exponential Continuous Non-Parametric Neural Identifier With Predefined Convergence Velocity
- Exploring Image Generation for UAV Change Detection
- Wearable Robots for Human Underwater Movement Ability Enhancement: A Survey
- A Scalable Adaptive Approach to Multi-Vehicle Formation Control with Obstacle Avoidance
- Distributed Fault-Tolerant Consensus Tracking of Multi-Agent Systems Under Cyber-Attacks
- Adaptive Control With Guaranteed Transient Behavior and Zero Steady-State Error for Systems With Time-Varying Parameters
