A Linear Algorithm for Quantized Event-Triggered Optimization Over Directed Networks
2022-06-25YangYuanLiyuShiandWangliHe
Yang Yuan, Liyu Shi, and Wangli He,
Dear Editor,
This letter investigates a class of distributed optimization problems with constrained communication. A quantized discrete-time eventtriggered zero-gradient-sum algorithm (QDE-ZGS) is developed to optimize the sum of local functions over weight-balanced directed networks. Based on an encoder-decoder scheme and a zooming-in technique, an event-triggered quantization communication is designed. Theoretical analysis shows that the exact convergence to the global optimal solution is guaranteed when the triggering threshold is bounded and the scaled sequence introduced by the zooming-in technique is quadratic summable. When the scaled sequence is bounded by an exponential decay function, QDE-ZGS converges linearly to the unique global optimal solution. Numerical simulations are conducted to demonstrate the theoretical results.

Most of literature, including aforementioned ones, heavily relies on the accurate state information, which inevitably brings great challenges for the communication capacity due to bandwidth constraints. To address this problem, the quantized communication was deployed widely in the network environment [8]. On this front,the zooming-in based quantized communication was introduced for average consensus subject to constrained data rate [9]. Leveraging the same mechanism, a series of subgradient based distributed optimization algorithms have been designed under constrained communication over undirected [10] and directed networks [11],[12], where only sublinear convergence was guaranteed. For the linear convergence, auxiliary-variable quantized algorithm was developed [13], resulting in the inevitable increase of computation cost. For a communication-efficient algorithm, it is expected to achieve fast convergence with less computation cost.
Besides, based on the fact that communication is contributed to more energy consumption compared with computation [14], the data transmission at every iteration puts strict requirements on the communication capacity, which is beyond the ability of agents with limited energy. Considering the communication bandwidth limitation, the event-triggered communication mechanism has been introduced from distributed control [15], [16] into distributed optimization [17], [18]. Based on the zooming-in technique, an event-triggered quantized communication mechanism was developed in [19] over time-varying communication networks, which is not applicable over fixed networks. A distributed constrained optimization problem was solved through the zooming-in technique based event-triggered quantized communication in [20]. The authors in [21]focused on the same problem in the continuous-time setting and inexact convergence was achieved. It should be noted that only the sublinear or asymptotic convergence was guaranteed in [19]-[21]. It is of practical significance to design a linear convergence algorithm with constrained communication.
Motivated by above discussions, this letter incorporates the eventtriggered quantized communication mechanisms into the discretetime ZGS algorithm and the linear convergence is achieved over directed networks. The main contributions are summarized as follows:
1) A zooming-in based event-triggered quantized communication mechanism is designed, where only the bounded triggering threshold is required.
2) The exact convergence is achieved under event-triggered quantized communication on the condition that the scaled sequence introduced by the zooming-in technique is quadratic summable.
3) When the scaled sequence is bounded by an exponential decay function, the linear convergence is established, which is faster than other quantized algorithms [10], [11], [13] and event-triggered based algorithms [19]-[21] without any auxiliary variables.





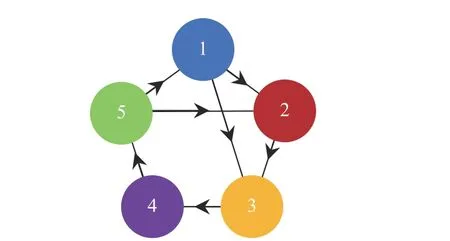
Fig. 1. Communication network.

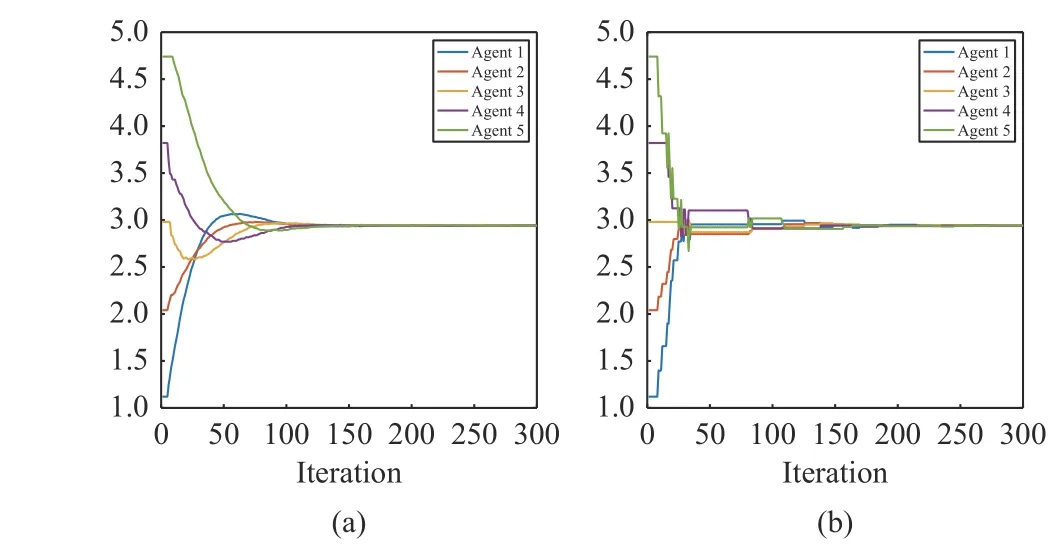
Fig. 2. Time evolutions of state xi,i ∈V for different s(k) . (a)s(k)=10/(k+1) ; (b) s (k)=10×0.98k.
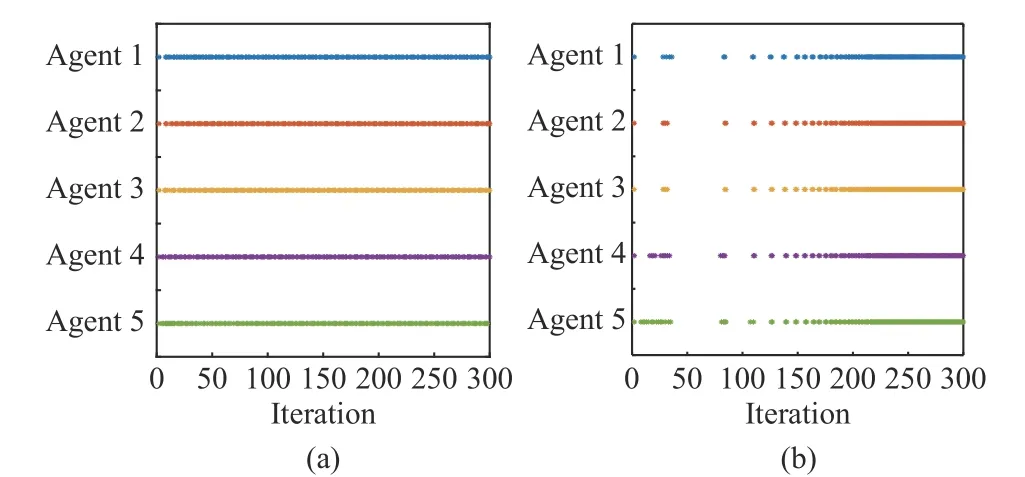
Fig. 3. Triggering instants for different s(k) . (a) s(k)=10/(k+1); (b)s(k)=10×0.98k.
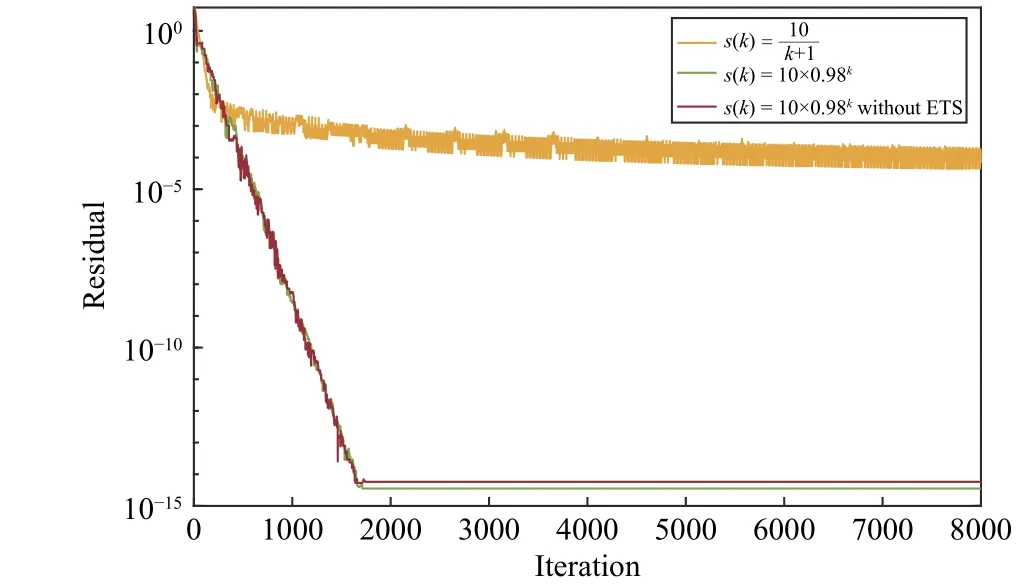
Fig. 4. Performance comparison.
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Exponential Continuous Non-Parametric Neural Identifier With Predefined Convergence Velocity
- Exploring Image Generation for UAV Change Detection
- Wearable Robots for Human Underwater Movement Ability Enhancement: A Survey
- A Scalable Adaptive Approach to Multi-Vehicle Formation Control with Obstacle Avoidance
- Fuzzy Set-Membership Filtering for Discrete-Time Nonlinear Systems
- Distributed Fault-Tolerant Consensus Tracking of Multi-Agent Systems Under Cyber-Attacks
