Adaptive Control With Guaranteed Transient Behavior and Zero Steady-State Error for Systems With Time-Varying Parameters

Hefu Ye and Yongduan Song,

Abstract—It is nontrivial to achieve global zero-error regulation for uncertain nonlinear systems. The underlying problem becomes even more challenging if mismatched uncertainties and unknown time-varying control gain are involved, yet certain performance specifications are also pursued.In this work, we present an adaptive control method, which,without the persistent excitation (PE) condition, is able to ensure global zero-error regulation with guaranteed output performance for parametric strict-feedback systems involving fast time-varying parameters in the feedback path and input path. The development of our control scheme benefits from generalized tdependent and x-dependent functions, a novel coordinate transformation and “congelation of variables” method. Both theoretical analysis and numerical simulation verify the effectiveness and benefits of the proposed method.

I. INTRODUCTION

WE consider the following SISO nonlinear systems with fast time-varying parameters [1]:

However, real-word engineering systems with fast timevarying parameters are frequently encountered. For instance,the value of a circuit resistor might change with temperature,and some morphing aerial vehicles are normally designed with varying structures and parameters in order to complete some specific tasks, where the parameters might change with time or system states swiftly [11], [12]. For these types of systems,traditional adaptive methods might not be able to ensure desired control performance in terms of transient behavior and convergence accuracy, or even maintain the stability of the system. Efforts have been made (see, for instance [13] and[14]) in developing adaptive control methods with the aid of persistence of excitation to achieve exponential stability of linear time-varying systems. In [15], it is shown that the PE condition is not necessary to stabilize a linear time-varying system. The results in [16] and [17] implement the asymptotic/exponential tracking of robotic systems with/without time-varying parameters. In [18]-[20], along with observer based adaptive control, a projection algorithm is proposed to ensure the boundedness of the slow time-varying parameter estimate. In the context of adaptive control for time-varying nonlinear systems, [21] explores a soft sign function based approach to deal with unknown time-varying parameters. Recently, an elegant method based on the“congelation of variables” method is proposed in [1]-[3] to asymptotically stabilize a class of nonlinear system with fast time-varying parameters, which is further extended to address multi-agent systems in [22] and [23]. Thus far, meaningful results on adaptive control of systems with unknown and fast time-varying parameters are still limited, rendering the underlying problem interesting yet challenging.

In this note, we address the stabilization problem of fast time-varying system as described in (1) and our goal is to achieve zero-error full state regulation while at the same time maintaining global output performance, i.e., regulating each state to zero asymptotically and meanwhile confining the convergence process of the output within a prescribed boundary. Our development consists of three major steps: i)disassociating the recursive controller design from the initial condition of system (1) via two generalized functions and a novel coordinate transformation, thereby obtaining a global prescribed performance controller; ii) designing adaptive laws via the “congelation of variables” method to estimate fast time-varying parameters involved in the constrained systems;and iii) separating the lumped nonlinear terms and exploiting additional nonlinear damping terms in each virtual control input to completely offset the undesired perturbations caused by unknown time-varying control gain to achieve asymptotic convergence. With this comprehensive treatment, output convergence transient behavior is well preset and asymptotic(zero-error) regulation is achieved in the presence of mismatched time-varying uncertainties.

Unlike most prescribed performance control methods that only achieve uniformly ultimately bounded (UUB) stability for nonlinear systems with unknown but constant parameters[24]-[32], the proposed method ensures zero-error stabilization and global output performance for systems with fast time-varying parameters and mismatched uncertainties.

II. PRELIMINARIES

A. Two Useful Functions and Coordinate Transformation

B. Control Objective

III. MOTIVATING EXAMPLE

Consider the following first-order system2:

VI. SIMULATION

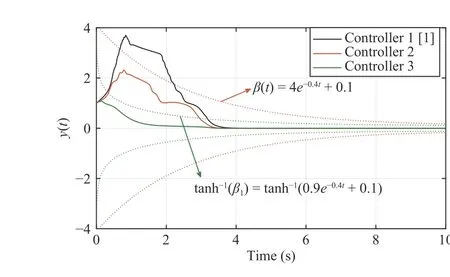
Fig. 1. The evolution of y (t).

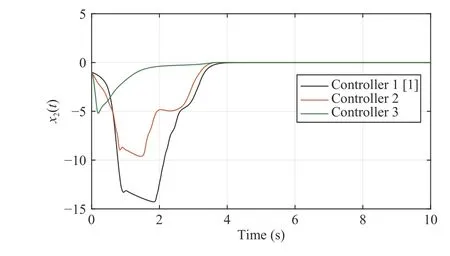
Fig. 2. The evolution of x2(t).

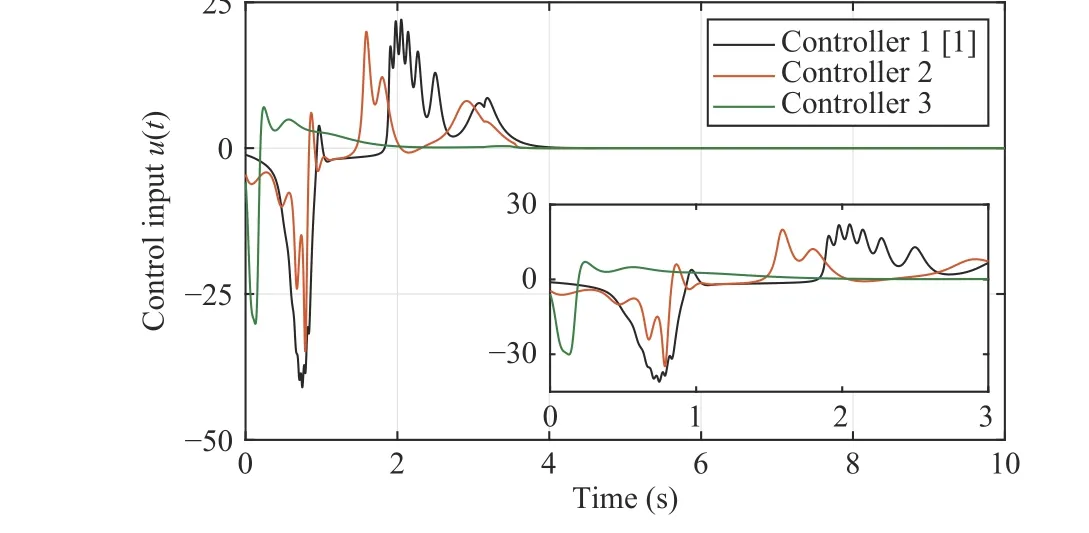
Fig. 3. The evolution of u (t).

To verify the effectiveness of the proposed control method,we consider the following system3:a counterintuitive phenomenon, that is, a faster system response can be achieved without increasing the control effort for the same choice of controller parameters. In short, all results show that the proposed methods are powerful enough to stabilize the nonlinear system with fast time-varying parameters.

VII. CONCLUSION

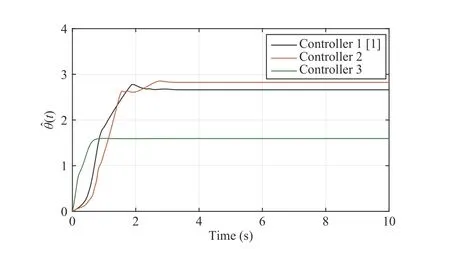
Fig. 4. The evolution of θ ˆ(t).

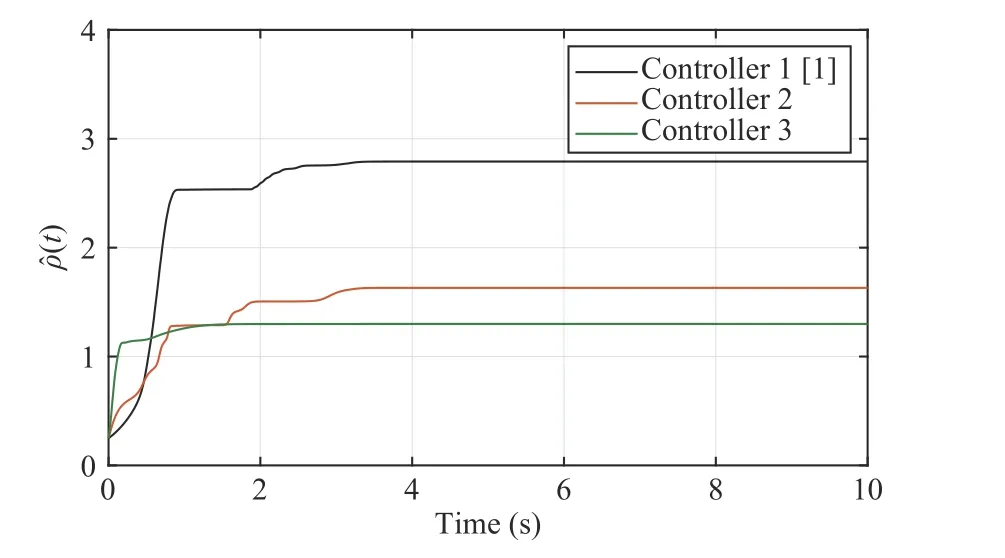
Fig. 5. The evolution of ρ ˆ(t).

Fig. 6. System time-varying parameters θ (t) and b (t).

This work presents an adaptive control strategy with guaranteed performance for strict-feedback nonlinear systems involving fast time-varying parameters. It is shown that with this strategy, not only each system state is regulated to zero asymptotically, but also the system output is strictly confined within an exponentially decaying boundary, making system output well behaved during the transient period and steadystate phase. We start with a simple scalar system with timevarying parameters in the feedback path and input path to illustrate our core idea in addressing time-varying parameters and output performance constraints simultaneously. By using classical backstepping technology and nonlinear damping, we then extend our method to a higher-order system and remove the need for overparametrization. Furthermore, the diversity of performance function selection and the diversity of normalized function selection together with the independence on initial conditions imply the universality of our controller,and simulation comparisons confirm the effectiveness and benefits of these methods.

Prior to this work, the prevailing wisdom in adaptive control in the context of exponential stability for time-varying systems was that certain persistent excitation conditions(sufficiently rich signals) must be present. Here in this work we develop a method that achieves exponential convergence,pointwise in time, without the need for PE conditions.Interesting future research topics include studying exponential/finite-/prescribed-time regulation of nonlinear systems with unknown time-varying parameters and control directions,studying robustness with respect to external disturbances via adaptive disturbance rejection, and borrowing the ideas in[38]-[40] to explore the distributed control of multiagent/large-scale systems with time-varying parameters.