Fixed-Time Lyapunov Criteria and State-Feedback Controller Design for Stochastic Nonlinear Systems
2022-06-25HuifangMinShengyuanXuBaoyongZhangQianMaandDemingYuan
Huifang Min, Shengyuan Xu, Baoyong Zhang, Qian Ma, and Deming Yuan
Abstract—This paper investigates the fixed-time stability theorem and state-feedback controller design for stochastic nonlinear systems. We propose an improved fixed-time Lyapunov theorem with a more rigorous and reasonable proof procedure.In particular, an important corollary is obtained, which can give a less conservative upper-bound estimate of the settling time. Based on the backstepping technique and the addition of a power integrator method, a state-feedback controller is skillfully designed for a class of stochastic nonlinear systems. It is proved that the proposed controller can render the closed-loop system fixed-time stable in probability with the help of the proposed fixed-time stability criteria. Finally, the effectiveness of the proposed controller is demonstrated by simulation examples and comparisons.
I. INTRODUCTION
AS is well-known, many practical systems are nonlinear;e.g., robot systems, inverted pendulums, tunnel diode circuits, etc. The controller design of nonlinear systems has attracted increasing attention in the past few decades and many useful tools have emerged [1]-[10]; for example, the backstepping technique [1], the addition of a power integrator method [2], the Lyapunov function criteria method [3], the prescribed performance control (PPC) method [4]-[6], and so on. Since stochastic noises extensively occur in real engineering field, the investigation of stochastic nonlinear systems is necessary and significant. Due to good transient response performance, the backstepping technique has been successfully extended to stochastic nonlinear systems in [11],which together with basic stochastic stability theories[12]-[14] allows for remarkable developments on the controller design and analysis of stochastic nonlinear systems;see, [15]-[25] and the references therein.
Considering the faster convergence speed, higher accuracies, and better disturbance rejection ability of finite-time stability, it is rather meaningful to ensure stochastic nonlinear systems converge in finite time. To this end, [26]-[29] made the first attempt to establish the definitions of finite-time stability for stochastic nonlinear systems and obtained the related Lyapunov theorems. Then, based on the finite-time stability theory, the finite-time controller design has obtained many results in [30]-[35] for stochastic nonlinear systems in various structures. In [36], a general Lyapunov theorem of stochastic finite-time stability and some important corollaries with more general conditions were further presented.Recently, a definition of semi-global finite-time stability in probability was presented in [37] and a related stochastic Lyapunov theorem was established to state-feedback stabilize stochastic nonlinear systems with full-state constraints.
However, the bound estimate of the settling time in finitetime control is dependent on system initial states. This impedes its practical applications since the estimate of the settling time and desirable characteristics cannot be derived without knowledge of initial conditions. As an evolution of the finite-time control, the fixed-time control whose settling time estimate is independent of a system’s initial states has gradually attracted scholars’ attention. In [38], the fixed-time control technique was used to handle stability issues of linear systems. Since then, fixed-time control was frequently considered for deterministic systems in [39]-[42].
For a stochastic nonlinear system, the fixed-time prescribed performance on the output tracking error was investigated by developing a novel performance function and using traditional Lyapunov bounded in probability stability [43]. Motivated by finite-time stability in probability using the Lyapunov criteria,the authors established the concept of fixed-time stability and used the Lyapunov theorem for stochastic nonlinear systems in [44]. Then, [45] used it to study the global fixed-time stabilization of switched stochastic nonlinear systems and [46]considered stochastic pure-feedback nonlinear systems. In[47], the fixed-time controller was designed for stochastic interconnected nonlinear large-scale systems. However, the obtained upper-bound of the settling time is conservative in[44]-[47]. Motivated by the above discussions, two natural issues arise: Can we further improve the proof of the fixedtime Lyapunov theorem in [44]? How do we use it to stabilize stochastic nonlinear systems with a less conservative settling time?
This paper aims to solve the above two issues. The contributions are listed as follows:
1) An improved fixed-time Lyapunov theorem with more reasonable and rigorous proof is given for stochastic nonlinear systems.
2) A corollary with a less conservative bound estimate of the settling time is obtained.
3) Based on the backstepping technique and the addition of a power integrator method, a state-feedback controller is skillfully designed for a class of stochastic nonlinear systems.By using the proposed fixed-time stability criteria, it is proved that the proposed controller guarantees the closed-loop system to be fixed-time stable in probability.
The remainder of this paper is organized as follows. Section II gives the preliminaries. A fixed-time stability theorem is given in Section III. In Section IV, the state-feedback controller is designed and analyzed. Section V shows an example, which is followed by Section VI to end this paper.
Notations:Throughout the whole paper, R+is the set of the non-negative real numbers; Ristands fori-dimensional Euclidean space;XTdenotes the transpose of a given vector or matrixXand ‖X‖ denotes its Euclidean norm withTr{X}being its trace whenXis square; Cirepresents the family of all the functions with continuousith partial derivatives; a classK function is continuous, strictly increasing and vanishes at zero; K∞is the set of all functions γ(x) which are of classK and radially unbounded (γ (x)→∞asx→∞).
II. MATHEMATICAL PRELIMINARIES





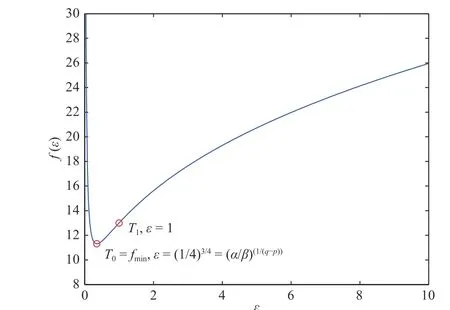
Fig. 1. The response of f(ε).
IV. STATE-FEEDBACK CONTROL FOR STOCHASTIC NONLINEAR SYSTEMS


A. Controller Design
The following coordinate transformation is given to start the design procedure:


B. Stability Analysis
The following theorem shows the stability given by the designed controller.


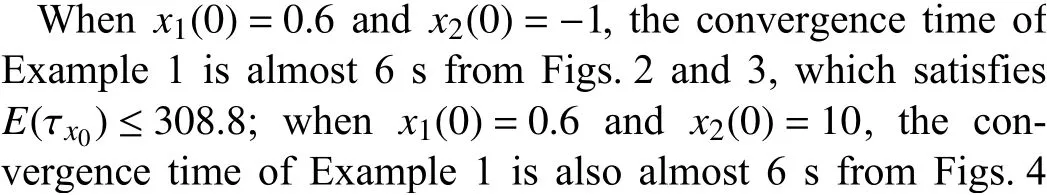
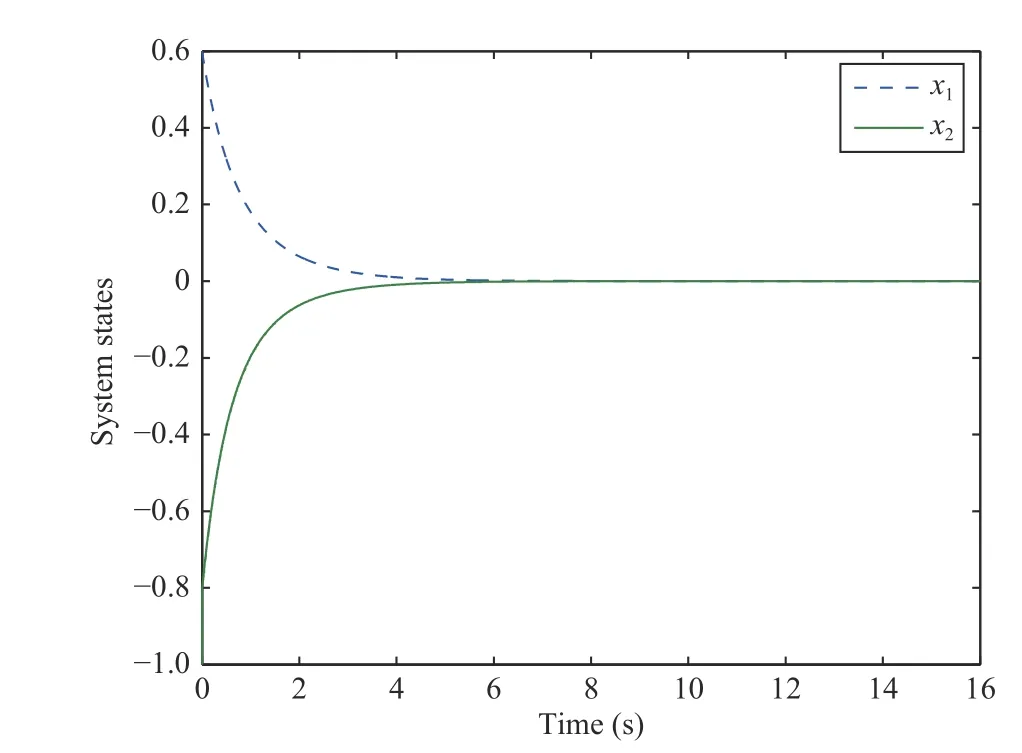
Fig. 2. The response of states with x 1(0)=0.6 and x 2(0)=-1.
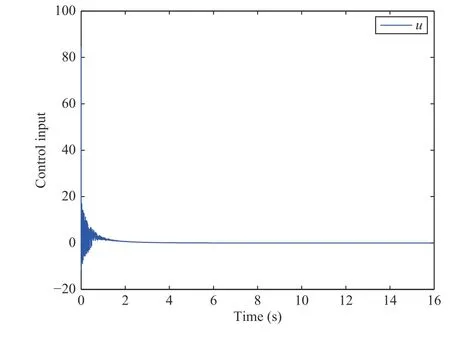
Fig. 3. The response of control input with x1(0)=0.6 and x 2(0)=-1.

Fig. 4. The response of states with x 1(0)=0.6 and x 2(0)=10.

Case 2:To show the difference between fixed-time (FxT)control and finite-time control, we show the finite-time (FT)controller given by [32] as

Fig. 5. The response of controller with x1(0)=0.6 and x2(0)=10.

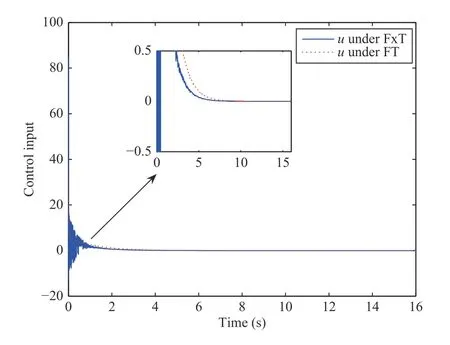
Fig. 6. The response of controller with x1(0)=0.6 and x2(0)=-1.
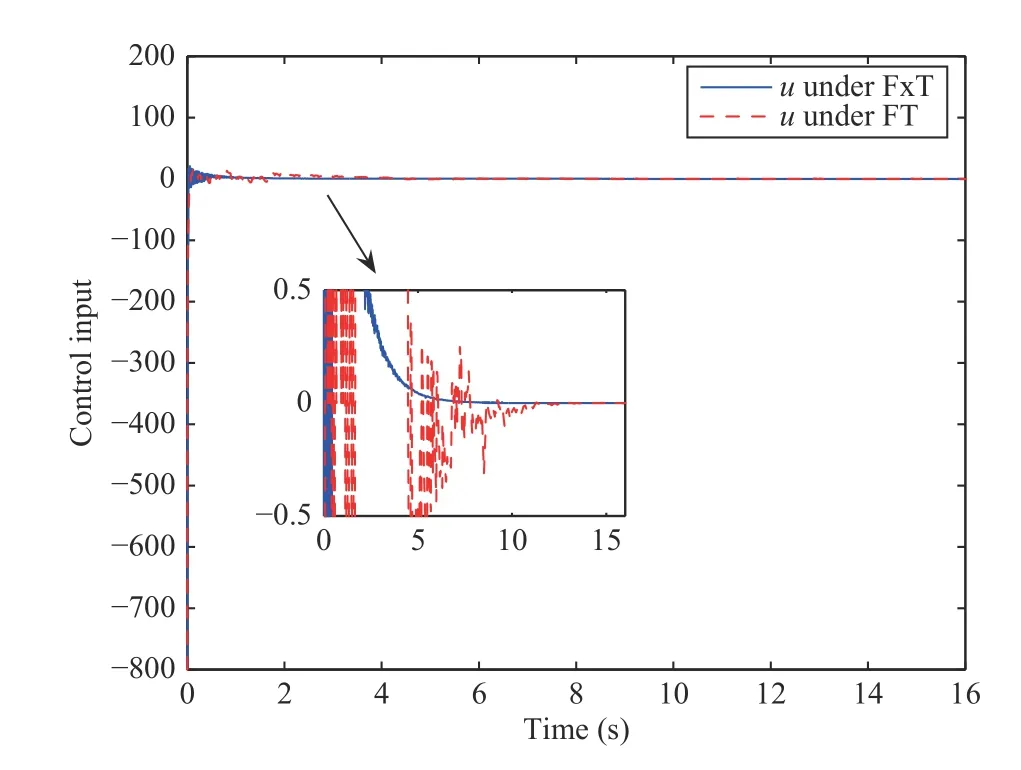
Fig. 7. The response of controller with x1(0)=0.6 and x2(0)=10.


Fig. 8. The response of Example 2.
VI. CONCLUSIONS
In this paper, the Lyapunov criteria of fixed-time stability for stochastic nonlinear systems has been improved.Compared with existing results, the upper-bound estimate of the settling time is less conservative with rigorous and reasonable analysis. In addition, with a backstepping design, a state-feedback controller is designed for stochastic nonlinear systems, which ensures the closed-loop system to be fixedtime stable in probability. There are still problems to be investigated: i) Determining how to use the proposed stability to give the output-feedback controller design for more general stochastic nonlinear systems. ii) For stochastic nonlinear systems with inverse dynamics, determining how to obtain the fixed-time stability theorem and design the controller.
APPENDIX
Proof of Proposition 1:Firstly, from (19), (26) and Itô’s rule, one has




杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Exponential Continuous Non-Parametric Neural Identifier With Predefined Convergence Velocity
- Exploring Image Generation for UAV Change Detection
- Wearable Robots for Human Underwater Movement Ability Enhancement: A Survey
- A Scalable Adaptive Approach to Multi-Vehicle Formation Control with Obstacle Avoidance
- Fuzzy Set-Membership Filtering for Discrete-Time Nonlinear Systems
- Distributed Fault-Tolerant Consensus Tracking of Multi-Agent Systems Under Cyber-Attacks
