改进适应度遗传算法在泵站优化调度中的应用
2022-06-25符向前
李 娜,符向前
(1.中国灌溉排水发展中心,北京 100054;2.武汉大学动力与机械学院,武汉 430072)
0 引 言
泵站是水利工程建设中的关键设施,随着我国泵站规模的扩大和工程规模愈发复杂,泵站优化运行理论和实践有待进一步深化研究。由于泵站调度存在较多非线性影响因素,且具有多阶段规划运行和多属性的特点[1],如何设计泵站最优调度策略,成为实现泵站经济稳定运行的关键。
针对上述问题,相关领域的研究人员对此展开了深入的研究和探索。其中,在泵站调度优化算法领域,动态规划法、神经网络算法、遗传算法、模拟退火算法、粒子群算法等均得到了有效的实践应用。不少学者从耗电量最小或费用最低为优化目标,利用动态规划算法对泵站调度模型优化求解[2-4]。魏良良等[5]以泵站的实际运行数据和水泵水力特性为基础,设计BP神经网络模型进行数据训练,以水泵的最小运行功率为训练目标,计算满足最小运行功率下的泵站调度方案。吴帮等[6]提出的基于混合粒子群算法的泵站最优灌排模型设计以灌排量平衡理论为基础,在满足泵站安全运行要求的前提下,采用线性加权法构建最优灌排优化调度模型,并利用动态规划法针对泵站的动态运行参数进行分析,最终采用粒子群算法计算最优灌排量。另有不少学者采用遗传算法对城市供水泵站调度模型进行求解计算,制定了最优泵站运行方案[7,8]。
遗传算法结合随机选择的偶然性和生物遗传的必然性特点,能在搜索过程中获取和积累搜索空间的相关知识,并自适应控制搜索过程,以求得最优解[9]。传统遗传算法由于自适应函数的正态分布特性,易导致早期收敛,陷入局部最优。本文采用一种基于顺序非线性的改进适应度遗传算法,求解泵站优化运行模型,通过其实际表现,验证了该改进算法的有效性。
1 泵站调度模型
1.1 水泵基本性能曲线
水泵的基本性能曲线包括流量-扬程曲线、流量-功率曲线、流量-效率曲线三种。为准确描述水泵的基本性能,采用数学描述法进行描述,即在额定工作参数下,对泵站的各性能曲线进行拟合。
针对流量-扬程曲线的拟合,本文采用二次抛物线法,拟合方程为:

式中:H为扬程;Q为水泵的流量;a0、a1均为拟合参数。
流量-功率曲线采用如下公式进行拟合:

式中:P为水泵的运行功率;b0、b1、b2均为拟合参数。
流量-效率曲线采用如下公式进行拟合:
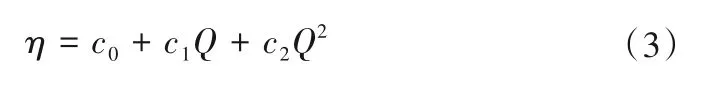
式中:η为水泵运行效率;c0、c1、c2均为拟合参数。
以水泵的比例率为基础,采用调速比进行相似率表示,表示结果如下:

式中:K为调速比;QN、HN、PN为水泵基本性能上的点。
综合上述公式可得,在不同水泵运行参数下,水泵的流量-扬程曲线可表达为:

流量-功率曲线可表达为:

流量-效率曲线可表达为:

1.2 泵高效运行区间
通过调节水泵调速比增加原水泵的高效运行区间以适应泵站运行的不同工况,高效运行区间由原来定速泵最高效率点附近10%,扩展到一个范围区间[8]。从图1可知,水泵高效区间在ABCD范围内。

图1 水泵高效运行区间
1.3 目标函数和约束条件的设定
泵站优化调度是指在满足时段需水量和扬程等约束的前提下,设定泵站运行优化目标,在此目标和约束条件下,计算泵站整体最优调度的运行参数,得出最优运行方案。
1.3.1 目标函数
本文以时段内泵站最小耗电量为目标函数,其目标函数的定义式可表达为:

式中:F表示时段内泵站最小运行耗电量;n表示泵站水泵台数;ρ和g分别为水的密度和重力加速度,本文均取标准值。Qi和Hi分别表示第i台泵的流量和扬程;ηimot和ηi表示第i台水泵机组的电机效率和水泵工作效率;m表示泵站运行时段;Tj表示第j个时段的时长。
1.3.2 约束条件
(1)扬程约束。各水泵扬程应满足最低进出口水位差约束,且满足在水泵的高效区间运行。本文各水泵并联,因此满足:

式中:HΔ为泵站进出口水位差。
(2)流量约束。泵站运行需满足时段内调水量需求,且每台机组流量在过流能力区间内。为达到最优目标,应让流量在满足过流能力的基础上,在泵的高效区间运行,即:

式中:Q为供水量;Qmin和Qmax分别为泵高效区间运行的流量下限和上限。
2 改进适应度函数的遗传算法理论
2.1 遗传算法介绍
遗传算法是一种结合进化论和群体遗传论的全局自适应搜索算法,利用遗传算法进行求解其本质是以生物进化机制为基础实现全局优化搜索,其优势在于可从群体角度出发进行最优解搜索,相对一单角度搜索寻优能力更强,可针对多个峰值进行比较,整体收敛性较强,便于获取全局最优解,相较于其他寻优算法,针对复杂性、非线性数学概念的优化问题处理具有一定的优越性。
基于遗传算法的目标最优求解过程,是按照一定编码规则把待求解问题排列为字符串形式,引入遗传学理论,每一个字符串对应遗传学中一个单独的染色体,不同的染色体构成一个染色体种群。首先初始化染色体种群,初始化的目的是使染色体种群中每一个染色体具有一个函数适应值,然后经过选择、交叉、变异等遗传操作,不断进行染色体种群迭代和净化,直至生成待求解问题的最优解。具体步骤如图2所示。
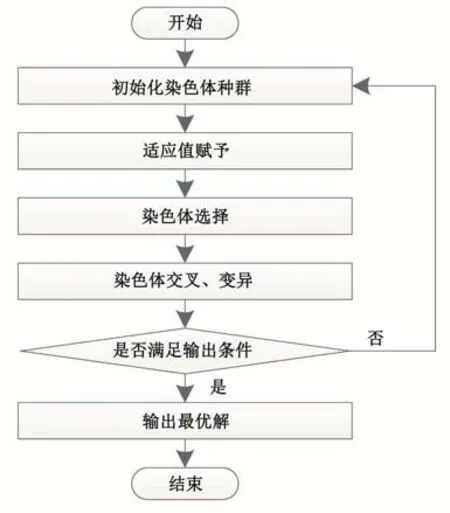
图2 遗传算法求解步骤
步骤(1):在一定约束条件下对染色体种群进行初始化,采用向量u对每一个染色体进行编码,向量u的分量可理解为遗传学上的基因,该基因对应的染色体的某一决策向量。
步骤(2):根据目标函数和约束条件每一条染色体所对应的目标函数值,该目标函数值被称为对应染色体的适应值,适应值的大小决定该染色体适应程度,也是决定该染色体的可利用价值。
步骤(3):根据染色体的适应值大小按照从高到低的顺序进行排列,选择适应值较高的染色体生成优质染色体群进行繁殖。
步骤(4):通过交叉、变异等基本遗传操作产生子代染色体,其中,突变操作生成的染色体子代具有双亲没有的突变基因。
步骤(5):更新染色体种群,重复步骤(2)~(4),每一个染色体的适应值不再发生变化时,即可输出全局最优解。
2.2 遗传算法的适应度函数改进
适应值的选取,决定了染色种群的可利用价值。通过选择合适的适应度函数,能加快目标函数寻优效率,且避免陷入局部最优解。当适应度函数的设计不当时,为了加快最优寻解,在算法最开始迭代时,就选出了一些较优的个体,这些个体的存在,进一步左右后续迭代,导致整个寻优过程,一开始就可能朝着局部最优的方向发展,陷入早熟收敛。基于顺序的适应度函数的构造方法[10],将目标函数值进行降序排列,然后将顺序排好的个体按照映射关系,计算相应的适应值。因此,通过该适应度函数选择的个体仅与其个体在种群中的位置有关。适应度函数如下:

式中:i表示种群按优劣排序后的个体顺序值;β为适应度参数,一般取值0.01~0.3之间。
由此可知第i个个体被选中的概率为:

将式(11)代入式(12),分子分母约去β,再令α=1-β,其中α∈(0,1),则适应度函数可表示为:

3 基于改进适应度遗传算法的泵站优化调度
以某取水泵站为例,该泵站安装了4 台KP16203-DV 型号水泵机组,额定扬程30 m,额定流量0.63 m3/s,电动机功率250 kW,电动机效率0.96。由此可知,泵站单日最大供水量为21.8万m3。
3.1 调度模型
采用最小二乘法对机组的流量-扬程曲线和流量-效率曲线进行拟合,拟合方程分别如式(14)和(15)所示:

泵站日常取水量16.9 万m3,日耗电1.94 万kWh。在满足日常最低取水量的基础上,基于式(8)、(9)、(10)、(14)、(15)建立泵站日调度模型。该泵站4 台水泵均为变频泵,通过变频调速控制水泵运行。
3.2 模型求解结果
分别采用传统遗传算法(SGA)和本文设计的改进适应度函数的遗传算法(FFGA),对泵站日调度模型进行最优求解。为了避免单次结果受遗传个体的随机性选择干扰,分别对每个算法进行20 轮计算,每轮计算均设置种群规模150,最大迭代次数800次。
3.2.1 寻优性能比较
SGA 和FFGA 两种算法求得的日最小运行耗电量如图3所示。
由图3可知,FFGA 和SGA 算法计算的20 轮平均耗电量分别为17 835 kWh和18 179 kWh,前者平均耗电量比后者平均耗电量低1.77%。虽然SGA 在第13 和19 轮结果好于FFGA,但稳定性较差,整体变异系数达到1.31%,远高于FFGA 算法的0.23%。由此可见,改进适应度函数的遗传算法不仅寻优稳定性更好,且能一定程度上避免早熟收敛,获得更优的结果。
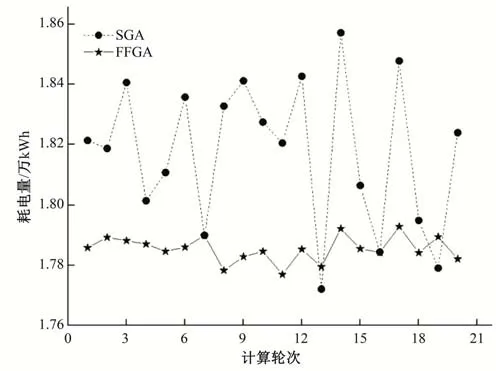
图3 耗电量比较
对比迭代次数,FFGA 平均迭代221 次达到收敛,比SGA 多29 次(图4)。这是由于SGA 算法在每轮遗传迭代过程中,倾向于按照初次分配的适应值的遗传方向迭代,因此迭代次数少于FFGA算法。

图4 迭代次数比较
3.2.2 泵站日运行方案
基于20 次FFGA 求解结果,取平均值,最终得到泵站日运行方案如表1所示。在满足日流量需求的前提下,4台机组24 h开机运行,总计功率743 kW,日耗电量比经验运行耗电省8.07%。

表1 泵站各机组日调度方案
4 结 语
(1)采用基于顺序的非线性函数,对遗传算法适应度函数进行改进,虽然造成寻优迭代次数增加,但能有效克服算法早熟收敛和不稳定性问题。
(2)通过泵站实际运行优化案例,证明了改进适应度函数的遗传算法(FFGA)能稳定地寻找到比传统遗传算法(SGA)更优的调度运行方案。以泵站日运行总耗电量为目标函数,FFGA 得出的泵站耗电量相比SGA 和通过经验制定的运行方案分别低1.77%和8.07%。
