枞阳仿自然鱼道水流条件优化数值模拟研究
2022-06-25胡乔一王晓刚
祝 龙,胡乔一,王 程,王晓刚
(1.南京水利科学研究院,南京 210029;2.通航建筑物建设技术交通行业重点实验室,南京 210029;3.长江勘测规划设计研究有限责任公司,武汉 430000)
0 引 言
引江济淮工程地跨皖豫两省,涉及江淮两大水系,是国务院要求加快推进建设的172项节水供水重大水利工程之一。然而闸坝等水利工程的建设在给人们带来社会效益和经济效益的同时,也破坏了河湖的连通性,阻碍了鱼类在河湖中的自由通行,破坏了原有区域的生态平衡,为此需要修建过鱼设施[1-4]。引江济淮工程枞阳引江枢纽过鱼设施的建设,便是为了恢复长江干流与菜子湖之间的鱼类洄游通道,满足江湖洄游鱼类的入湖和出湖需求,起到江湖鱼类资源互补,促进鱼类增殖和恢复鱼类种质资源的作用。考虑长河枞阳老闸段在引江枢纽建成后将废弃,因此工程拟利用此部分废弃河道改造为仿自然通道,利用原始边坡进行布置,由仿自然通道段、工程鱼道段及调节池组成,从而形成鱼类的上溯洄游通道。
仿自然鱼道是一类重要的过鱼设施,与传统工程鱼道不同的是,仿自然鱼道的断面结构比较复杂,其大多利用工程现场材料(地形特征、渠道底部物质及石块)来设计和建造,更加注重与生态环境的整体协调性,其目的在于尽可能满足不同鱼类的上溯要求,保护水生生物多样性,同时还可以形成景观廊道[5,6]。目前,国内外学者对于以竖缝式鱼道为主的工程鱼道研究较多。李秀萍等[7]论证了竖缝宽度对双侧竖缝式鱼道水力特性的影响。王晓刚等[8]分析了竖缝位置、池室长度、增设辅助隔板等对竖缝式鱼道直段休息池、转弯段休息池水动力特性的影响。董志勇等[9]则剖析了溢流堰和竖缝组合式鱼道水池内时均流速、紊动强度、雷诺应力、相关函数、紊动尺度等紊流结构。GAO等[10]采用一种欧拉-拉格朗日方法模拟了鱼道中虚拟鱼的运动轨迹。BALLU 等[11]研究了竖缝鱼道池室底部存在宏观粗糙度(混凝土圆柱体)对水流流动的影响。仿自然鱼道传承了隔墙竖缝的基本型式,对鱼道建筑材料和结构形式进行仿自然优化,其结构型式更趋于多样化。马卫忠等[12]对比了仿自然鱼道竖缝式和竖缝-表孔组合式两种不同结构型式的鱼道池室水力特性。李广宁等[13]定量分析了透水性卵石墙对鱼道水力特性的改善效果。王智娟等[14]对窄深型仿自然鱼道的收缩卡口布置和内部消能措施进行了一定研究。徐进超等[15]则建立了仿自然鱼道整体物理模型,论证了鱼道池室水流条件和深潭补水方案。由于其断面型式的多样化,边底材质粗糙,存在较多不确定性等原因,目前对于仿自然鱼道尚无完善的研究方法,因此设计难度较大。本文针对枞阳仿自然鱼道,采用概化模型的方式开展三维紊流数值模拟研究,初步判断鱼道内的水力特性,优化鱼道内部断面结构参数,获得相对较为合理的仿自然鱼道池室结构布置,为相关部门确定最终方案提供参考。
1 数学模型建立及验证
1.1 基本方程
数学模型采用RNGk-ε双方程模型模拟鱼道内复杂的紊流结构,其控制方程为:
连续方程:

动量方程:
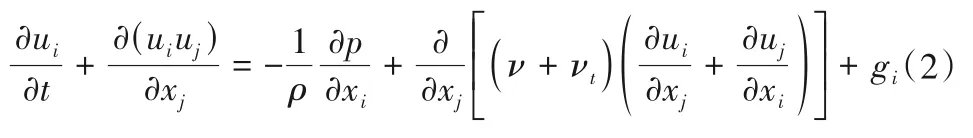
k方程:
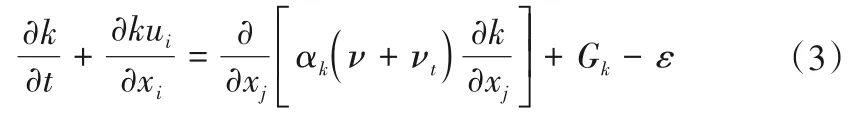
ε方程:
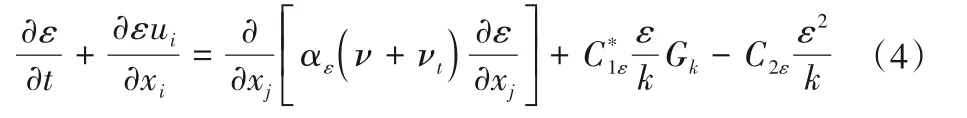
式中:ui和uj为速度分量,m/s;xi和xj为坐标分量,m;t为时间,s;ρ为流体密度,kg/m³;p为修正压力,Pa;ν为分子黏性系数,m2/s;νt为紊流黏性系数,m2/s,计算公式为νt=Cμk2/ε;gi为重力体积力,m/s2;k为紊动能,m2/s2;ε为紊动能耗散率,m2/s3;Gk为平均速度梯度引起的紊动能产生项,m2/s3;方程中的其他参数:
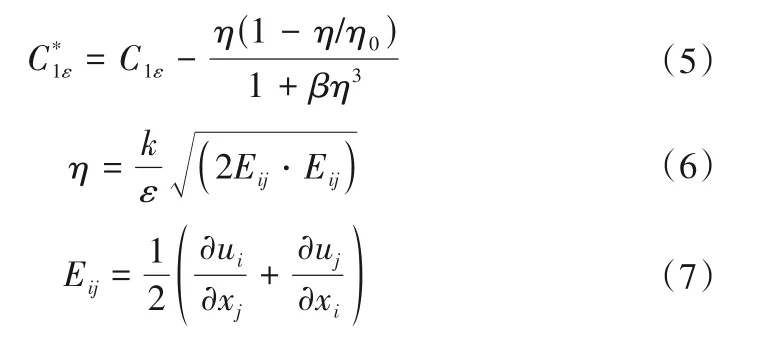
方程中的经验常数Cμ=0.084 5,αk=αε=1.39,C1ε=1.42,C2ε=1.68,η0=4.38,β=0.012。
采用VOF 方法捕捉水气两相流自由液面,求解如下输运方程:
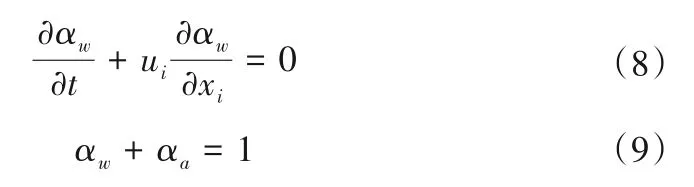
式中:αw表示液体的体积分数;αa表示气体的体积分数。
鱼道上下游计算边界设定为相同水深1.5 m,上表面边界为空气边界,其余边界为无滑移壁面,采用PISO 算法求解鱼道内瞬态水力特性直至计算稳定。
1.2 计算区域及网格划分
根据设计型式,仿自然鱼道采用梯形断面,渠底宽2 m,边坡为1∶2,底坡为1∶242,正常运行水深取1.5 m,每间隔10 m 布置一道隔墙,隔墙采用浆砌块石结构,隔墙厚度取0.8 m,隔墙过水断面为竖缝结构,竖缝宽1.0 m,竖缝中心偏离池室中心线距离(简称竖缝偏心距)为0,鱼道整体为连续弯道布置,以“三弯道一直道”布置分布。过鱼设施的设计流速是关系到鱼类是否可以通过的重要参数,通常是由过鱼对象的克流能力及鱼道的长度决定。根据相关部门提供的资料,本工程的过鱼对象较多,主要有四大家鱼、鳡鱼、长颌鲚、日本鳗鲡等,同时既有成鱼也有幼鱼,根据主要对象的克流能力,鱼道的设计流速指标取为0.7~0.9 m/s。
数值仿真概化模型计算区域包括17个普通池室以及上、下游各15 m 的平段,长度约200 m,鱼道数学模型如图1所示。因仿自然鱼道结构比较复杂,对计算区域采用四面体单元进行网格划分,对鱼道竖缝处进行局部加密,模型约136 万网格单元,网格划分情况如图2所示。鱼道竖缝流速为过鱼设计的关键,为了分析鱼道沿程缩窄断面的流速,选取图1中1号~12号竖缝及竖缝附近区域统计缩窄断面最大流速。本文开展的多组鱼道池室结构优化计算工况如表1所示,其中工况1 为原设计方案,针对鱼道内的水流条件,工况2~6 分别对鱼道池室长度、池室底宽、竖缝宽度以及竖缝偏心距进行优化(本文中鱼道池室边坡均取1∶2)。
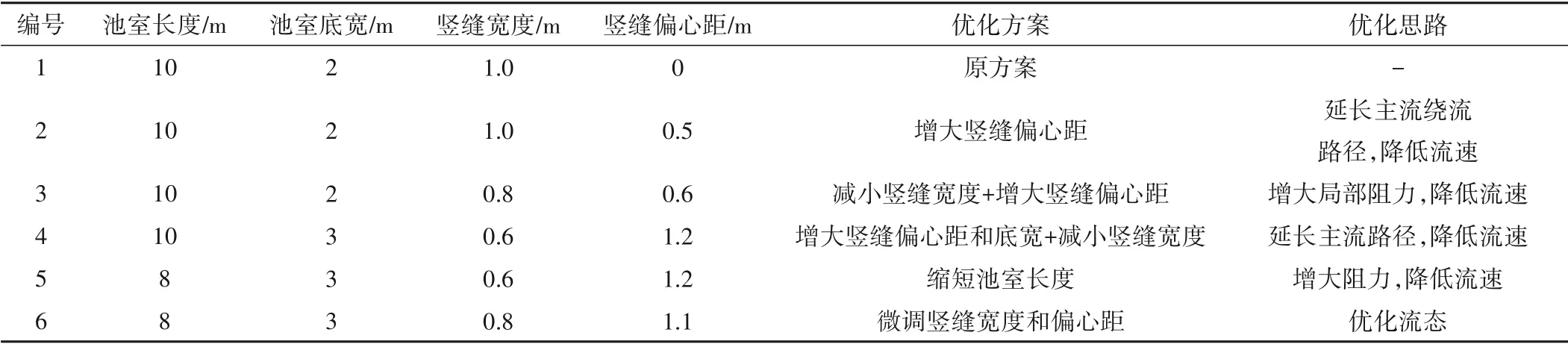
表1 鱼道数学模型计算工况Tab.1 Calculation conditions of fishway mathematical model
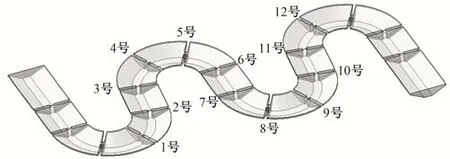
图1 鱼道数学模型Fig.1 Numerical model of fishway

图2 鱼道数学模型网格划分Fig.2 Simulation mesh of fishway
1.3 模型验证
枞阳仿自然鱼道物理模型包含约30 m长的工程鱼道段、整个过渡调节池和249 m 长的仿自然通道段,模型几何比尺为5。其中,仿自然通道段基本尺寸按照数学模型工况6 推荐的鱼道布置尺寸建立,即池室长度8 m,池室底宽3 m,竖缝宽度0.8 m,竖缝偏心距1.1 m(竖缝贴坡布置),试验中控制仿自然通道段中的原型水深为1.5 m。对鱼道设计中最为关键的缩窄断面最大流速进行验证,因物理模型中的弯道布置与数学模型存在差异,所以仅对物理模型和数学模型各缩窄断面最大流速的统计值进行验证,物理模型实测各缩窄断面最大流速最大值、最小值和平均值分别为1.03、0.72 和0.86 m/s,数学模型计算各缩窄断面最大流速最大值、最小值和平均值分别为1.04、0.71和0.89 m/s,两者差别不大,可见数学模型计算参数选取合理,可用于工程实际研究。
2 结果与分析
2.1 原方案鱼道池室水流条件
枞阳仿自然鱼道原设计方案(工况1)鱼道每级池室长10.0 m,底宽2.0 m,底坡1∶242,边坡1∶2,竖缝宽度1.0 m,竖缝偏心距为0 m。在该布置型式下,鱼道内整体流场分布如图3所示,鱼道池室局部不同水层流速分布如图4~图6所示,其中底层、中层、表层分别以0.2h、0.5h、0.8h进行划分(h为鱼道水深),本文图中左侧均为上游侧,右侧为下游侧。由图可知,由于底宽仅2.0 m,鱼道水深为1.5 m,整体下窄上宽的梯形断面构造使得鱼道内三维水力特性较为明显,因过水断面由底层向表层逐渐扩大,鱼道池室水流的扩散程度也依次上升,因此,鱼道底层的流速水平较高,中层次之,表层流速水平相对较低,表层水流相较中底层更为紊乱;在弯道作用下,鱼道沿程各池室流速存在一定的差异,弯道布置具有一定的消能作用,虽然竖缝偏心距为0,但池室内并未产生直冲射流,主流蜿蜒前进,在池室内绕行,各水层主流较为明确,在主流两侧存在不同范围的回流,回流区流速较低,可作为鱼类上溯的休息区域;水流在竖缝处存在一定的偏流集中效应,竖缝处流速分布不均,其最大流速主要位于竖缝附近偏下游侧,竖缝附近大范围流速在1.0 m/s 以上,整体流速较高,难以满足设计流速指标要求,需要进行优化。
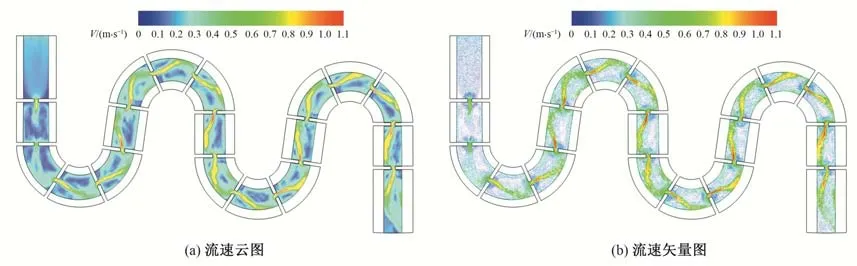
图3 鱼道池室整体流场分布Fig.3 Overall flow field distribution in fishway pools
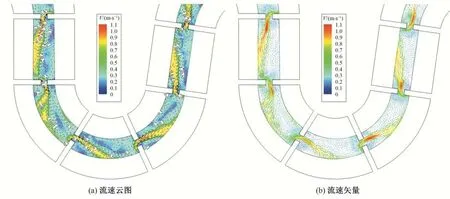
图4 鱼道池室底层流场分布Fig.4 Flow field distribution in the bottom layer

图5 鱼道池室中层流场分布Fig.5 Flow field distribution in the middle layer
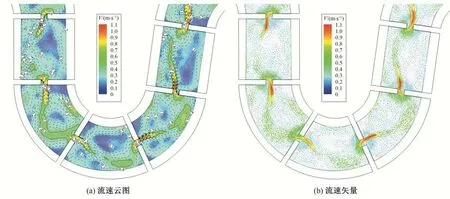
图6 鱼道池室表层流场分布Fig.6 Flow field distribution in the surface layer
2.2 优化方案鱼道池室水流条件
2.2.1 工况2~3鱼道池室水流条件
为了降低鱼道竖缝的流速,先从鱼道隔墙结构着手优化,即保持鱼道池室长度和池室底宽不变,将竖缝贴坡设置,即竖缝偏心距为0.5 m(工况2),仍保持竖缝贴坡设置,降低竖缝宽度至0.8 m(工况3),以鱼道池室中层为例,工况2~3鱼道池室水流条件如图7~图8所示,统计工况1~3 鱼道沿程各竖缝及附近区域最大流速如表2和图9所示。为了对竖缝内流速范围进行定量分析,选取2号、5号、8号、11号竖缝为典型断面,取每个竖缝下游侧边缘为统计断面,其位置示意如图10所示,每个统计断面上布置98 个测点,因鱼道的设计流速指标为0.7~0.9 m/s,定义流速超过0.7 m/s为大流速,以大流速点数占统计点数的比例为大流速占比,以此近似估计竖缝内的大流速范围。

图7 工况2鱼道池室中层流场分布Fig.7 Flow field distribution in the middle layer of fishway in condition 2
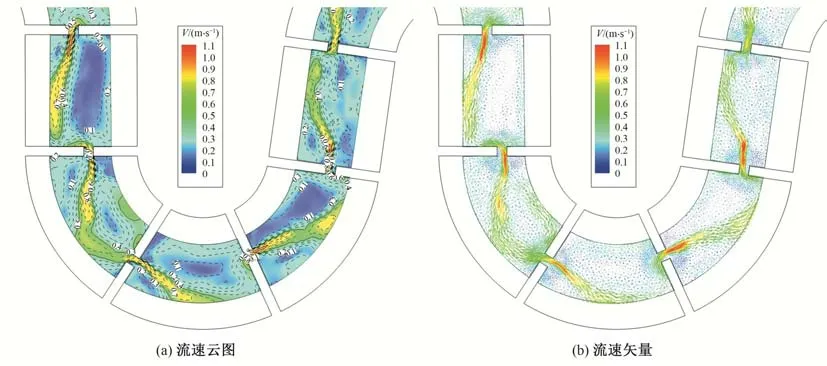
图8 工况3鱼道池室中层流场分布Fig.8 Flow field distribution in the middle layer of fishway in condition 3
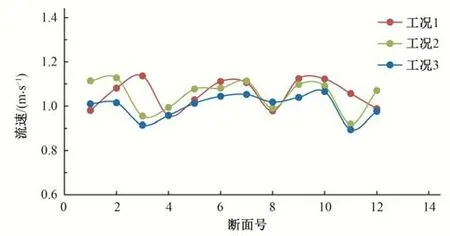
图9 工况1~3沿程竖缝区域统计最大流速Fig.9 Statistical maximum velocity along vertical slot area of fishway in condition 1~3

图10 竖缝下游侧边缘测量位置示意Fig.10 Measuring position of downstream edge of vertical slot
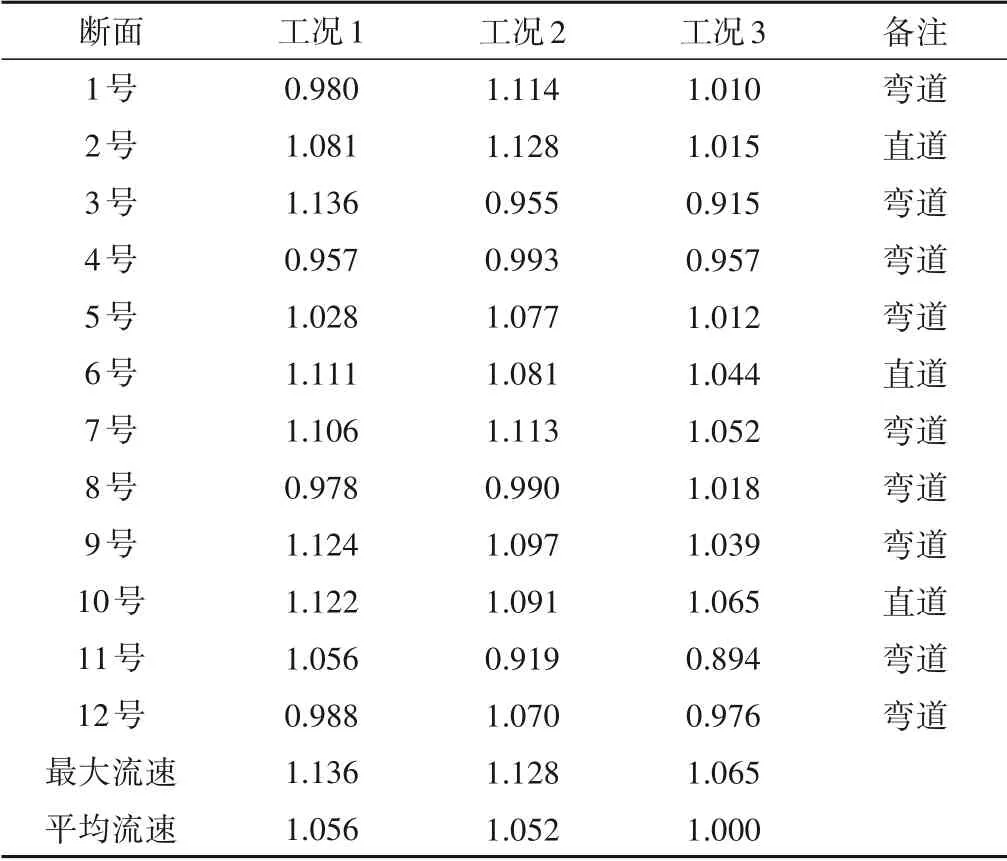
表2 工况1~3鱼道沿程竖缝区域统计最大流速 m/sTab.2 Statistical maximum velocity along vertical slot area of fishway in condition 1~3
由图表可知,工况2 鱼道内流速分布与原布置方案基本类似,在底宽为2.0 m 的情况下,增大竖缝偏心距对竖缝处流速影响不明显,工况1 和工况2 竖缝附近区域的最大流速分别达到了1.136 和1.128 m/s,最大平均流速分别达到了1.056 和1.052 m/s,竖缝最大流速远超设计流速0.7~0.9 m/s 的要求,竖缝处流速分布不均,根据统计结果,超过0.7 m/s 的大流速范围基本占全断面50%左右。究其原因,是由于竖缝宽度达到1.0 m,宽度过大,导致水流通路过大,消能不够充分,所以需考虑减小竖缝宽度。减小竖缝宽度后的工况3 竖缝处流速有所降低,竖缝附近统计最大流速和平均流速分别为1.065 和1.000 m/s,设计流速指标仍不满足要求,大流速范围仍占50%左右,需要进一步优化。
2.2.2 工况4~6鱼道池室水流条件
由于目前鱼道底宽较小,即使已将竖缝贴坡布置,实际上相邻池室竖缝之间的间距并不大,水流在池室内部偏转有限,致使竖缝处消能仍显不足,无法满足设计流速条件,特别是在直道池室,竖缝流速较高,仍有形成类似直冲射流的隐患。考虑到鱼道设计流速仅为0.7~0.9 m/s,与目前工况计算流速仍有较大差距,工况4 进一步将竖缝宽度减小至0.6 m,并将底宽拓宽至3.0 m,竖缝仍然贴坡布置(竖缝偏心距1.2 m),其计算结果如图11所示。由图中可知,该工况竖缝处流速得到了明显改善,但仍有一定范围的流速超标,竖缝偏心距较大,局部主流显得较为扭曲,但由于池室内流速并不高,回流并不剧烈,鱼类能够比较容易地找到主流完成上溯。综合考虑,该工况仍不能很好地满足设计要求,还需进一步对鱼道池室结构进行优化。
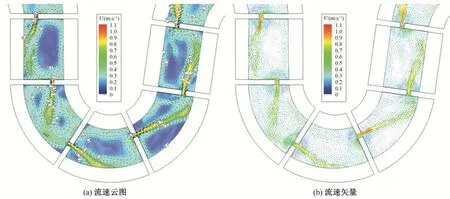
图11 工况4鱼道池室中层流场分布Fig.11 Flow field distribution in the middle layer of fishway in condition 4
为此,在上一个工况的基础上将鱼道池室长度缩短至8.0 m,其余保持不变(工况5)。计算结果如图12所示。由图中可知,随着池室长度的缩短,单位池室消耗的水头减小,鱼道竖缝处的流速得到了进一步改善,目前鱼道竖缝处最大流速基本在0.9 m/s 以下,存在较大范围可上溯的流速通道,局部流速虽略有超标,但超标范围不大,能够满足设计流速要求。在弯道以及竖缝异侧贴坡布置等影响下,鱼道池室内水体较为紊乱,各池室流速和流态存在较为明显的差异,部分池室主流趋于池室中央,部分池室水流偏转比较明显,总体上各池室能够形成较为明确的主流,使鱼类能够寻其方向完成上溯,在主流两侧存在不同程度的回流,大部分回流流速在鱼类感应流速以下,基本不会对过鱼产生太大影响,即鱼道池室内形成了相应的“大流速区”和“小流速区”,可以满足鱼类上溯的基本要求。
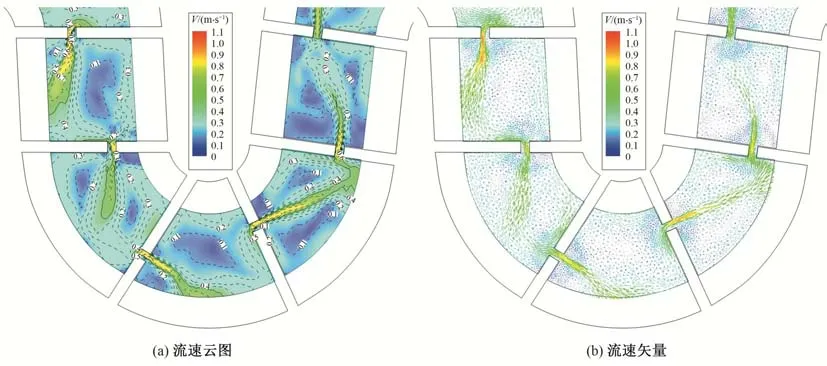
图12 工况5鱼道池室中层流场分布Fig.12 Flow field distribution in the middle layer of fishway in condition 5
考虑到工况5部分池室水流偏转较大,水流流态略为紊乱,本文补充了工况6 的计算,即在工况5 的基础上,加宽竖缝宽度为0.8 m,结果如图13所示。从中可以看出,鱼道池室内水流流态较前述工况有所改善,水流更为平顺,坚缝处有局部区域最大水流流速超过了0.7~0.9 m/s 的设计流速指标,但竖缝处水流本身流速分布不均,在竖缝加宽至0.8 m 后,控制断面大部分区域流速仍在0.9 m/s 以内,分析认为,该工况亦能够基本满足设计要求。
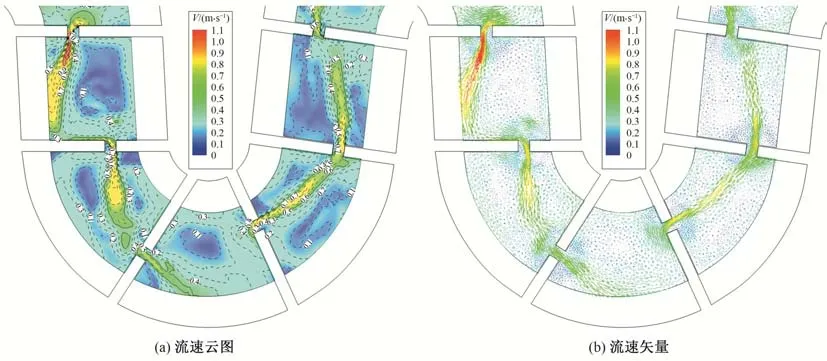
图13 工况6鱼道池室中层流场分布Fig.13 Flow field distribution in the middle layer of fishway in condition 6
以上优化工况(工况4~工况6)鱼道沿程竖缝附近区域最大流速统计如表3和图14所示。从图表中可以看出,当竖缝宽度为0.6 m,底宽3.0 m,竖缝贴坡设置时,鱼道沿程竖缝区域最大流速和最大平均流速分别达到了1.035 和0.946 m/s,较之前工况有了较大的改善,但仍然在设计流速标准以上,根据统计结果,典型竖缝断面大流速范围(0.7 m/s 以上)占比仍在50%左右,当进一步缩短池室长度至8.0 m 时,流速降低比较明显,其最大流速和最大平均流速分别降低至0.945 和0.849 m/s,竖缝区域最大流速基本能控制在0.7~0.9 m/s 之间,满足设计流速指标,典型竖缝断面大流速范围占比最大为38%,存在较大范围可供上溯的流速通道;在此基础上,将竖缝加宽至0.8 m,沿程竖缝区域最大流速和最大平均流速分别为1.039 和0.886 m/s,流速指标虽有所上升,但最大平均流速仍能够控制在0.9 m/s 以下,典型竖缝断面大流速范围也比较小,综合前述分析结果,可以认为该工况基本满足设计流速指标。
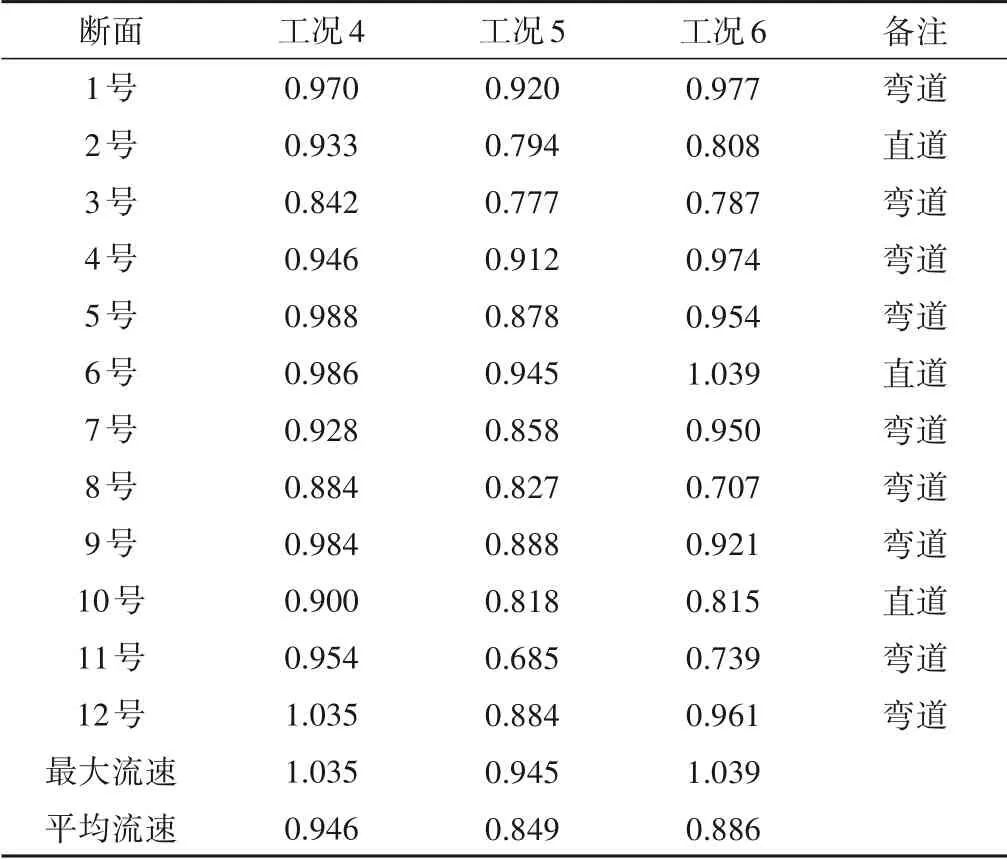
表3 工况4~6鱼道沿程竖缝区域统计最大流速 m/sTab.3 Statistical maximum velocity along vertical slot area of fishway in condition 4~6
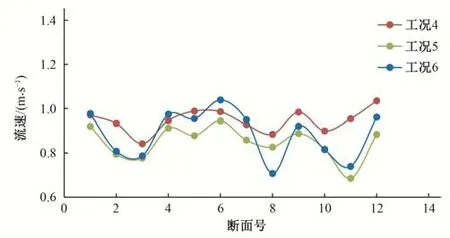
图14 工况4~6沿程竖缝区域统计最大流速(单位:m/s)Fig.14 Statistical maximum velocity along vertical slot area of fishway in condition 4~6
综合上述计算结果,推荐枞阳仿自然鱼道池室结构布置参数为:竖缝宽度0.6~0.8 m,底宽3.0 m,竖缝贴坡设置,即竖缝偏心距1.1~1.2 m,池室长度8.0 m。
3 结 语
仿自然鱼道比传统工程鱼道更能满足生物多样性的要求,在实际工程中越来越受到人们的重视,限于仿自然鱼道断面结构的复杂性,目前尚缺乏完善的研究手段。本文以枞阳枢纽仿自然鱼道为例,对“连续弯道布置”的鱼道池室建立三维概化紊流数学模型,优化池室内水流条件,获得的主要成果如下。
(1)提出了仿自然鱼道水流条件的优化思路:通过增大竖缝偏心距,延长主流绕流路径,减小竖缝宽度,增大局部阻力,缩短池长,增大池室级数,增大阻力等措施可降低池室流速,满足鱼类上溯需求;
(2)仿自然鱼道水流流态受到弯道、竖缝宽度、竖缝偏心距、池室底宽、池室长度等综合影响,流态复杂,在利用各种措施消能降低流速时,应控制主流弯曲度,避免上下池室竖缝中心线偏离过大,引起流态紊乱;
(3)对于仿自然鱼道,由于竖缝宽度较宽,即使竖缝区域最大流速超标,依然有可以上溯的流速通道;
(4)经过5种方案的逐步优化,推荐了枞阳仿自然鱼道隔墙布置方案,该方案下,鱼道池室水流条件良好,沿程竖缝区域最大流速基本能够控制在0.7~0.9 m/s,池室内主流明确,能够形成明显的“大流速区”和“小流速区”,满足过鱼基本要求,相关研究策略能够为类似工程提供参考。
