基于METRIC理论的超大规模卫星星座多级备份策略

骆天溯, 赵灵峰, 冯蕴雯,*, 薛小锋, 路 成

(1. 西北工业大学航空学院, 陕西 西安 710072; 2. 中国科学院微小卫星创新研究院, 上海 201203;3. 复旦大学航空航天系, 上海 200433)

0 引 言

传统的星座备份策略的应用对象为小型星座,卫星数量少、单颗卫星可靠度高、故障次数少,因此只需考虑使用少量备份卫星,采用一级或两级备份策略即可满足星座性能要求。而在超大规模低轨星座普及的今天,星座中卫星的数量是传统星座中的几十倍上百倍。同时,由于卫星的小型化以及运载火箭运力的提升,在实际工程中往往采用一枚火箭将多颗卫星送入轨道(一箭多星)的技术来降低发射成本。在星座的实际运行过程中,为了保证星座持续高性能运行,将卫星进行备份是一种常见且有效的手段,特别是在建设超大规模卫星星座中,设计者为了降低制造成本以及缩短制造时间通常会选择可靠性较低的商业元器件而非宇航级元器件,这导致了相较于传统小规模卫星星座,超大规模星座中的卫星在运行过程中更易出现失效,也凸显出备份策略之于超大规模低轨卫星星座的重要性。以铱星星座为例,在最初发射的一批卫星中有20颗需要更换,备份卫星数量占据了星座总卫星数量的30%。随着星座规模的不断增大,卫星失效次数也会逐渐增多,传统卫星星座备份策略对于这些庞大星座的求解效率以及适用度都很低,因此亟需提出一种新型备份策略来保证星座运行时的性能。

国内外学者对星座备份策略和可维修备件多级保障库存技术(multi-echelon technique for recoverble item control, METRIC)理论的研究十分广泛并取得了一定的成果。在多级备件库存优化中一个非常重要的问题就是如何确定各级库存点的备件数量。METRIC模型最早由Sherbrooke于1968年建立,该模型假设所有设施都有充足的修理能力,并服从库存控制策略,模型目标是在库存投资费用约束下,使预期延迟订货最小。Sherbrooke基于METRIC模型开发了一个能够寻找在横向供应下预期延期订货的准确近似值的仿真程序。Rustenburg把备件的供应分为初始供应和再供应两个过程,以费用为约束条件,用Petri网分别模拟了这两个过程并建了相应的数学模型。Thonemann等建立了以单个及多个备件订单的完成率为约束的库存模型,且根据该模型设计了一种求解模型的启发式算法。Willem等研究了以可靠性为中心的维修(reliability centered maintenance, RCM)过程,提出了以RCM过程中的费用数据来决定备件短缺费用的方法。上述文献均为METRIC方法论奠定了理论上的基础,然而由于时间久远且没有实际应用,因此不能直接用于解决超大规模星座备份的问题。

METRIC模型被广泛地应用在了各领域的复杂系统上。在航空领域,Muckstadt以民用飞机发动机为研究对象,考虑多订单、多备件情况,建立了以最小化订货成本为优化目标的METRIC模型。薛陶等以民用飞机为研究对象,建立了考虑资源共享以及备件报废的飞机修理级别和备件联合优化模型。冯蕴雯等结合准更新理论、排队论和VARI-METRIC模型提出了考虑维修比例的民机可修件多级库存规划方法。Wong等基于航空货运公司的真实数据研究了基于横向供应和等待时间约束的多级备件供应模型。在船舶领域,Sleptchenko和Rustenburg等将METRIC理论应用于海军舰船装备保障,建立了舰船备件的多级库存分配模型。阮旻智等在METRIC理论的基础上建立了备件的初始库存优化模型,并通过海军装备研究算例表明分层边际优化算法可大幅提高运算效率。在其他装备领域,王乃超等研究了多约束条件下备件库存优化问题,建立了多约束条件下备件库存优化模型并给出了优化算法。Bachman等针对美国航空航天局(National Aeronautics and Space Administration, NASA)未来太空探索需求研究备件保障问题,根据太空探索工具的特点将体积和质量约束加入到优化模型当中。由上述文献可见,METRIC模型在各种大型系统中有着诸多成熟应用的先例,但鲜有学者将METRIC模型应用在超大规模星座这一大型系统上,这是因为超大规模星座的概念最近才被重视并实践,因此METRIC模型在超大规模星座上的应用显得尤为重要。

传统的由少数高可靠度卫星组成的卫星星座备份策略的研究十分广泛,Thomas等通过研究Walker等多种星座构型建立了考虑“一箭三星”发射的100颗卫星规模的备份模型,并求解出最少备份卫星的配置方式。Lansard等通过研究大型通信卫星星座建立了以运行可用性为优化约束,发射费用和制造费用为优化目标的备份模型,从而获得考虑多标准的星座配置方案。Cornara通过研究全球卫星导航星座,建立了考虑星座发射策略、部署策略以及在轨重构过程的分别使用地面备份、停泊轨道备份和星座平面备份模式的备份策略,得出了各种备份模式的优缺点以及选择原则。Ereau考虑了火箭发射成功率和备份卫星失效率,建立了基于Petri网的星座模型,并求出最优的星座部署及维护策略。Kelley使用Markov模型来评估卫星系统的生命周期成本,提出了综合考虑采购、补给和运营成本因素下的星座备份模型。胡敏等进行了基于Petri网的Walker导航星座备份策略研究,给出了在轨和地面同时备份情况下的星座可用度计算模型。王尔申等提出了基于Markov过程的全球导航卫星系统(global navigation satellite system, GNSS)星座备份策略,并评估了不同数量的备份卫星对星座可用度的影响。侯洪涛对GNSS系统进行了多层可用性分析,并计算了考虑备份卫星时的星座可用性。上述文献中的研究对象均为不超过100颗卫星的小型星座,上述文献中的方法在应用于超大规模星座时存在着局限性,Markov模型和Petri网模型在对象超过1 000时会出现状态爆炸的问题,传统优化算法在处理超大规模星座问题时的计算时间十分冗长。

METRIC模型在卫星星座领域的应用尚不丰富。Menachem提出了基于(,)库存控制模型的通信卫星星座备份策略,然而该模型只考虑了星座平面的一级备份。Pauline提出了一种基于METRIC理论的同时考虑了3种备份模式的超大规模星座备份策略,使用(,)库存控制模型求解得到满足星座可用度指标且星座备份费用最低时的星座配置方案,然而模型中只考虑了星座平面和停泊轨道平面两级可用度,且未对结果进行边际效应分析,无法给星座决策者提供更全面的备份卫星配置方案。

本文提出了一种适用于超大规模星座的多级备份策略,同时使用地面备份、停泊轨道备份以及在轨备份3种备份模式对星座进行备份,并建立起以备份费用为优化目标,星座-停泊轨道-地面三级可用度为约束条件的星座备份模型,运用遗传算法(genetic algorithm, GA)对模型进行求解并使用边际分析法(marginal analysis, MA)分析了每个参数的边际效应,完成卫星在多级备份结构下的优化配置研究,最后运用某个超大规模低轨星座作为研究对象验证了方法的可行性和有效性。

1 问题描述与假设

随着星座系统的不断应用与发展,目前大规模星座系统的备份策略优化需求日益严峻。传统的星座备份策略考虑的卫星数量较少、故障次数较低且扩展性不足,除此之外还不能很好考虑一箭多星发射的情况,从而无法很好地适配如今的超大规模低轨星座。本文在这一工程背景下开展星座三级备份策略研究,其中三级是指备份模式为在轨备份、停泊轨道备份以及地面备份。星座三级备份示意图如图1所示。第一级备份为在轨备份。当一个星座轨道上的卫星发生故障时,使用可用的在轨备份卫星替换故障卫星,这个替换时间等于备份卫星从待机状态进入工作状态的时间,通常为几天。第二级备份是停泊轨道备份。备份卫星在较低高度的轨道上低功率运行,并且与星座轨道的倾角相同,当星座轨道中的备份不够充足时这些停泊轨道上的备份卫星将利用轨道机动转移到在轨备份中,替换时间为卫星等待轨道漂移时间加上轨道转移时间,这个时间一般会持续一到两个月。第三级备份是地面备份。该级备份由两部分组成,分别为火箭发射基地备份以及卫星制造厂备份。相同数量的备份卫星分别贮存在这两个备份地点。当星座平面卫星发生故障时火箭发射基地将备份卫星发射进入轨道,同时制造厂将备份卫星运输到火箭发射基地。备份卫星替换故障卫星的时间为发射场的发射订单处理时间加上火箭发射时间,这个时间一般会持续几个月到一年。

图1 星座三级备份系统Fig.1 Constellation three-level backup system

备份卫星在三级备份系统的转移流程如图2所示,当星座平面有卫星发生故障则会向第一级在轨备份发送订单补充备份卫星;当第一级在轨备份的卫星数量低于一定值(该值称为在轨备份订购点)后会向第二级停泊轨道发送订单补充备份卫星;当停泊轨道备份卫星数量低于一定值(该值称为停泊轨道订购点)后,会向地面备份发送订单补充备份卫星。

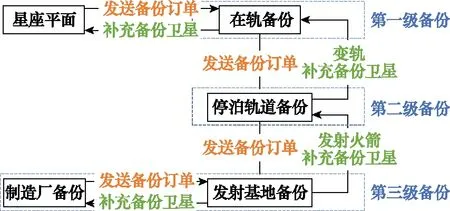
图2 备份卫星在各级备份之间的转移过程Fig.2 Transfer process of backup satellites between different levels

库存管理策略是星座备份策略的重要组成部分,超大规模低轨星座备份策略之所以采用(,)库存管理策略是因为该策略可以通过优化订购点以及订单数量以最大化“一箭多星”发射带来的费用优惠。(,)库存管理策略的补货周期如图3所示,每一级备份均贮存一定数量的备份卫星,当某一级备份卫星数量低于时就会向下一级备份发送数量为的备份订单,其中为订购点,为订单数量。

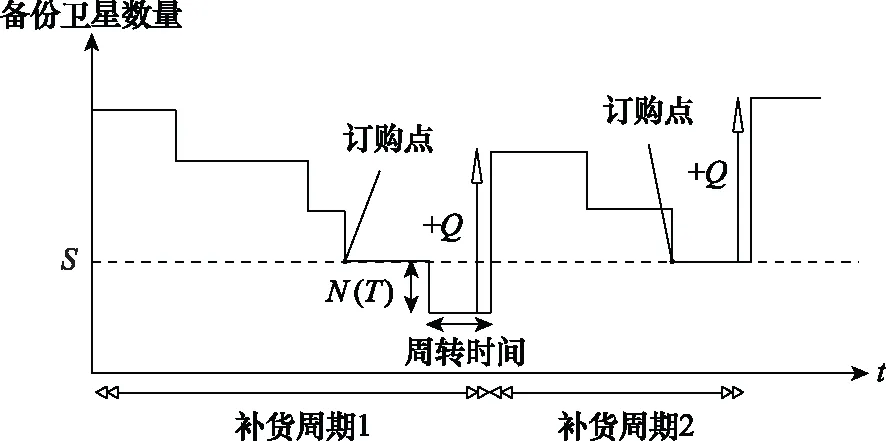
图3 (s,Q)备份卫星库存管理策略补货周期示意图Fig.3 Representation of replenishment cycles of (s,Q) backup satellite inventory management policy

为了简化建模过程及提高模型的工程适用性,对星座多级备份模型合理地做出以下假设:

(1) 在轨备份卫星替换故障卫星的时间忽略不计;

(2) 当一个星座轨道的备份卫星数量达到订购点时,同时向所有停泊轨道下达订单,由距离星座轨道最近的且有余量的停泊轨道供应该批备份卫星;

(3) 只有当前备份卫星订单处理完毕后才会处理下一个备份卫星订单;

(4) 所有卫星的变轨时间、变轨费用、发射时间、发射费用都相同;

(5) 在一段时间内卫星的失效数以及地面备份卫星缺货数均服从泊松分布;

(6) 不考虑卫星在运行期间以及备份期间发生共因失效的情况。

2 星座多级备份模型

2.1 备份费用模型

该模型是为了求解在满足可用度约束条件下最小的备份费用,总共考虑两种可能产生备份费用的方式:卫星制造费用以及卫星发射费用。这些费用的和称为星座年备份费用总和:

=+

(1)

211 制造费用

制造费用包含3部分,分别为卫星制造部分、卫星贮存部分以及卫星燃料部分:

=++

(2)

(1) 卫星制造费用

星座每年需要制造的备份卫星数量等于这一年内失效的卫星数量,由于卫星失效服从参数为的泊松分布,因此对于共有个轨道平面,第个平面上有颗卫星的星座,每年的制造费用计算如下：

(3)

式中:为每颗卫星的制造费用；为卫星失效率(次年);为星座轨道条数;为第条轨道上的卫星个数。

(2) 卫星贮存费用

卫星每年贮存费用主要指卫星在贮存期间相关人员及设备产生的费用,可分为两部分,一部分为地面贮存费用,一部分为空间贮存费用:

=+

(4)

① 假设制造工厂每年贮存一颗卫星的费用为,发射基地每年贮存一颗卫星的费用为,地面备份中卫星制造工厂以及发射基地的备份卫星数量均为颗,则地面贮存费用计算如下:

=(+)

(5)

② 星座轨道和停泊轨道上卫星每年的贮存费用主要与他们贮存的备份卫星平均数量有关:

(6)

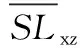
(7)

(8)

式中:为星座轨道每组备份卫星的个数;为停泊轨道每组备份卫星的个数;为星座轨道的订购点;为停泊轨道的订购点;为星座轨道备份组的数量;为停泊轨道备份组的数量;()为在周转时间内星座失效的卫星数量;()为在周转时间内星座失效的卫星数量;()=,()=。

由于地球不是一个均匀的标准的球体,会对运行在地球轨道上的卫星产生轨道摄动,使其轨道产生漂移现象,因此随着时间的推移,停泊轨道能够与任意的星座平面对齐,也就是说每条停泊轨道都能够为星座所有平面的故障卫星进行替换。替换时间计算如下:

(9)

其中,离待补给的星座轨道第近的停泊轨道到星座轨道的周转时间服从均匀分布:

(10)

(11)

霍曼变轨时间与初始轨道和目标轨道的半长轴的平均值(+)2有关,其中为初始轨道半径,为目标轨道半径。()为离待补给的星座轨道第近的停泊轨道有可用备份卫星的概率;为每条停泊轨道有可用备份卫星的概率;EBO()为在停泊轨道的备份卫星数量为时的期望短缺数。

(12)

(13)

(3) 卫星燃料费用

星座每年产生的燃料费用为每年所有卫星变轨消耗的燃料产生的费用:

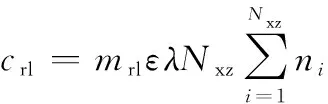
(14)

式中:为燃料质量转换系数;为变轨所需的燃料质量。为了节省变轨燃料,停泊轨道中的备份卫星只考虑使用霍曼转移方式进入星座轨道,计算公式如下:

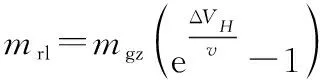
(15)

(16)

式中:为卫星干重;为卫星推进装置有效推进速度;Δ为变轨前后不同高度轨道的速度差。

212 发射费用

每年的发射费用与每年失效的卫星数量有关:

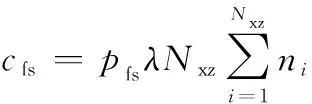
(17)

式中:为每颗卫星的发射费用。

2.2 星座可用度模型

221 卫星年平均需求量

年平均需求量是指星座在一年中需要替换的备份卫星数量,也指一年中星座中失效的卫星数量,计算公式如下:

(18)

式中:为第个星座平面中卫星的数量;FH为卫星每年运行时间;为星座轨道数量;MTBF为卫星的平均无故障间隔。

假设各星座轨道年平均需求量相同,则各星座轨道卫星年平均需求量为

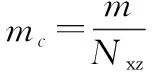
(19)

式中:为卫星在星座轨道的年平均需求量,=1,2,…,,为星座轨道数量。

各停泊轨道卫星年平均需求量:

(20)

卫星在停泊轨道的年平均需求量等于星座轨道申请的备份卫星需求之和,=1,2,…,,为停泊轨道数量。

发射基地备份年平均需求量:

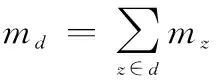
(21)

卫星在地面备份基地的年平均需求量等于停泊轨道申请的备份卫星需求之和,=1,2,…,,为地面备份基地数量。

222 期望需求量

期望需求量也称为供应渠道件数,指周转时间内发生的平均需求量。各地面备份基地卫星期望需求量:

=

(22)

式中:为从地面到停泊轨道的周转时间,计算公式如下:

=+

(23)

式中:为卫星从发射到停泊轨道的平均发射时间;为火箭发射基地平均订单处理时间。

各停泊轨道卫星期望需求量:

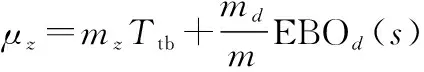
(24)

式中:EBO()为卫星在地面备份基地的备份卫星数量为时的期望短缺数。

各星座轨道卫星期望需求量:

(25)

式中：为卫星从停泊轨道到星座轨道的周转时间。

223 期望短缺数与星座可用度

期望短缺数是指在某一时间内未能满足供应的卫星需求数。根据METRIC理论,各地面备份基地卫星期望短缺数计算公式如下:

(26)

各停泊轨道卫星期望短缺数:

(27)

各星座轨道卫星期望短缺数:

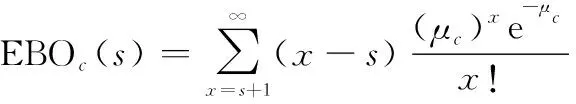
(28)

星座可用度是指在某一时间星座中正常运行的卫星所占的期望百分比,计算公式如下:

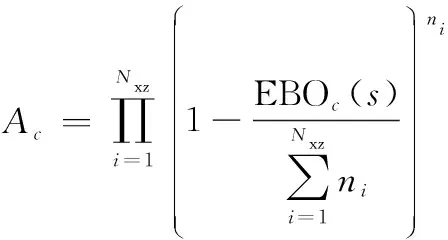
(29)

2.3 优化模型

研究卫星在轨备份策略的目的是在满足星座可用性的前提下使星座运行支持成本最低,因此建立以备份费用为目标函数,星座可用度不小于099且火箭一次发射搭载卫星的数目小于等于火箭运载能力为约束的优化模型:

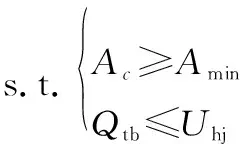
(30)

式中:为每年的总备份费用,可由式(1)计算;为星座轨道卫星可用度,可由式(29)计算;为保证星座正常工作的最低可用度要求;为一枚运载火箭可以搭载的卫星数目上限。

3 多级备份策略优化流程

超大规模卫星星座多级备份策略优化问题是一个复杂非线性混合整数优化问题,目标函数由多个复杂非线性函数构成且包含随机分布,优化参数同时包括整数及浮点数类型,优化约束同时包含非线性约束及线性约束,使用传统优化求解方法计算时间长且对计算机性能要求高。GA是一种高度并行、随机和自适应的智能优化算法。使用GA进行星座备份策略求解问题的流程如图4所示。

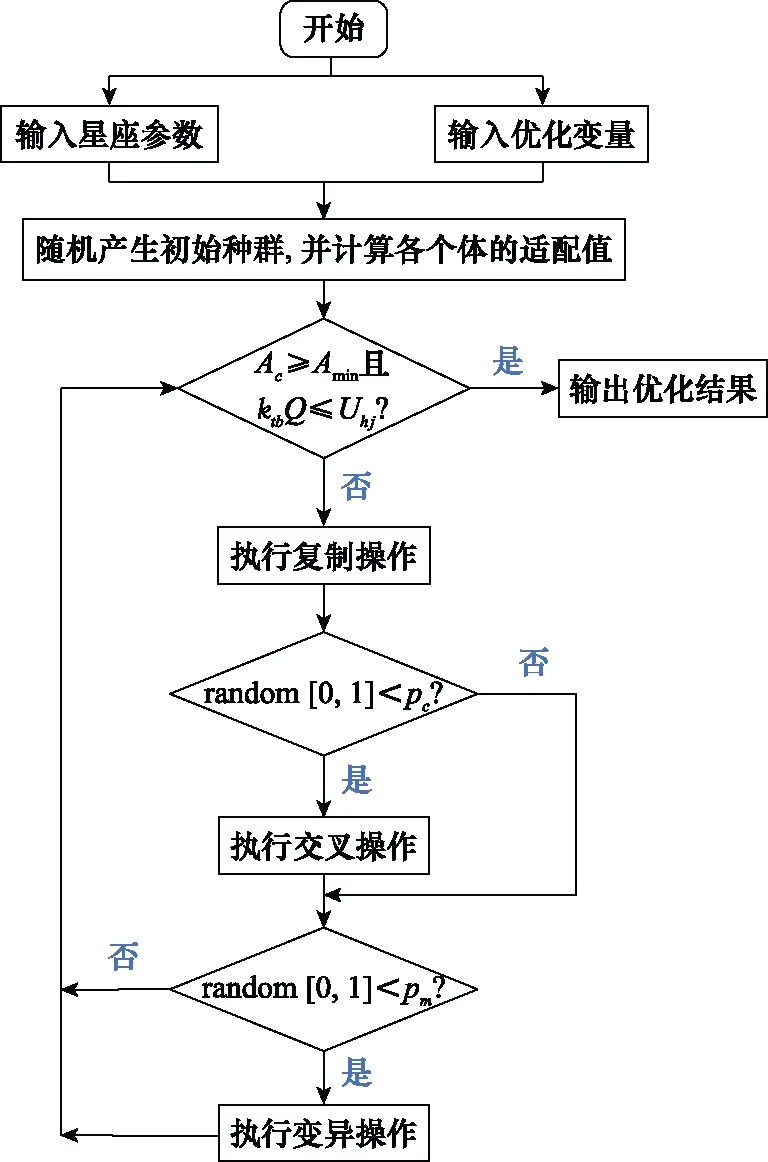
图4 GA求解星座多级备份策略优化流程图Fig.4 Optimization flow chart of constellation multi-level backup strategy using GA

使用GA求解的星座多级混合备份模型的求解步骤可描述如下：

输入星座固定参数及优化参数。

这些输入变量组成一个初始个体组,初始种群由一组初始个体构成,对每一个个体的适配值进行评价。

判断算法是否满足模型全部约束条件。若满足则将优化结果进行输出;否则执行步骤4～步骤7。

根据适配值大小以一定方式进行复制操作。

设定交叉概率并进行交叉操作。

设定变异概率并进行变异操作。

返回步骤4。

4 案例分析

4.1 输入参数

某星座由40条高度为1 200 km、倾角为50°的轨道组成,每条轨道上有40颗运行卫星,卫星的故障率为0.1(次/年),星座可用度指标为0.99,模型中的优化参数以及星座固定参数如表1和表2所示。

表1 模型优化参数

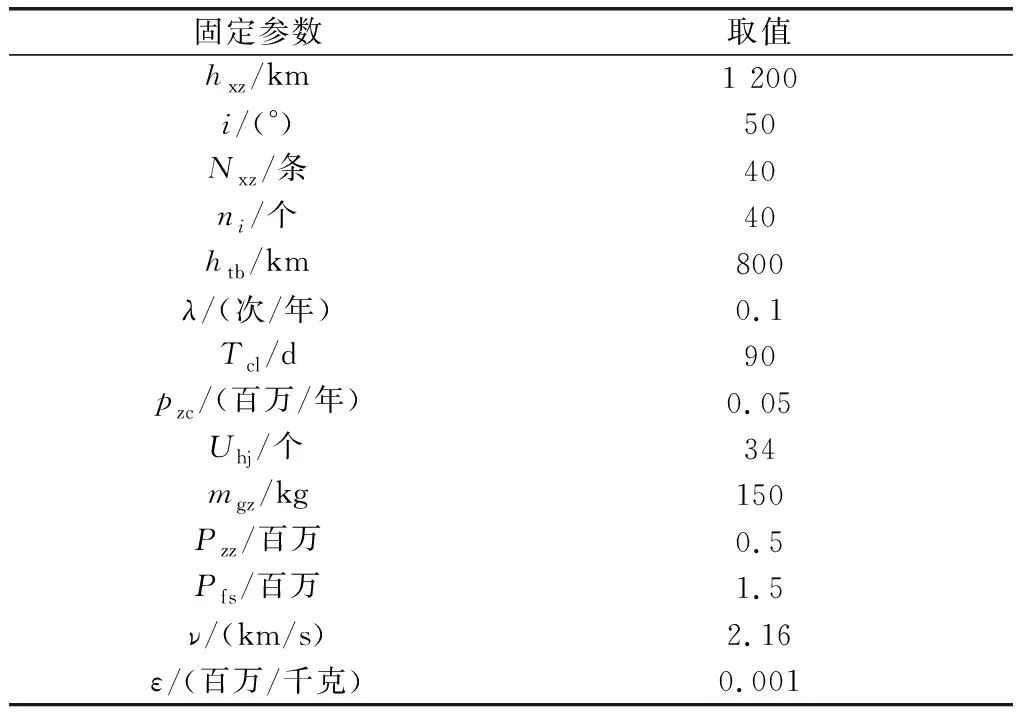
表2 星座固定参数

4.2 输出结果与分析

基于上述信息,依据式(1)可以得到星座每年的备份费用,根据式(29)可以得到星座可用度,在此基础上建立以备份费用为优化目标、星座可用度和火箭运载能力为约束的星座三级备份模型,利用GA对该模型进行求解,得出各级备份卫星的配置数量,其优化结果如表3所示。

表3 星座三级备份策略优化结果

根据以上结果可以得出,当前星座最优备份策略为:将3条停泊轨道部署在831.74 km高度处,星座轨道备份卫星低于1颗时从停泊轨道补充4颗卫星;当停泊轨道备份卫星少于40颗时从地面发射32颗备份卫星;发射基地以及卫星制造工厂各备份32颗卫星。此时,星座每年的总备份费用为464.32百万美元;星座可用度为0.995 0。

为了研究不同星座配置方式对星座可用度及备份费用的影响,使用MA法对不同输入参数带来的边际效应进行分析。根据第4.1节的计算结果,最优的备份策略为星座平面的备份卫星库存管理策略(,)=(1,4),停泊轨道平面的备份卫星库存管理策略(,)=(40,32)。

在,,与4个变量中,保持某3个变量不变的情况下,改变另一个变量以研究该变量下星座可用度与备份费用的边际效益。不同和值下的星座可用度随备份费用的变化关系如图5所示,不同和值下的星座可用度随备份费用的变化关系如图6所示。

图5 sxz与stb的边际效应Fig.5 Marginal effects of sxz and stb

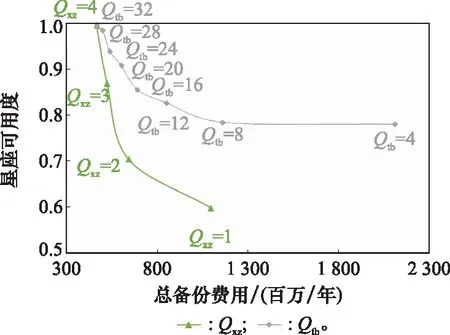
图6 Qxz与Qtb的边际效应Fig.6 Marginal effects of Qxz and Qtb

的定义域为1到20之间的所有整数,但是当>5时>34,即一次发射的火箭数量超过了运载火箭运力的限制,因此在图5与图6中没有相应计算结果。

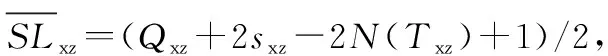
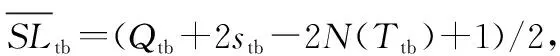
从图5两组数据对比来看,对于星座可用度的影响十分明显,而对总备份费用的影响并不显著,平均增加一组会增加003左右的星座可用度,而只增加6百万的备份费用。对备份费用的影响更为显著,而对星座可用度的影响并不明显,每增加一个会增加20百万的备份费用,而基本不增加星座可用度。因此,调整比调整可以为星座配置带来更好的边际效应。

从图6中可以看出,随着的增加,星座总备份费用在上升的同时星座可用度也随之上升,这是因为运载火箭一次发射的卫星数量越多,平均每颗卫星的发射费用会大幅降低,因此带来总备份费用的降低。而的增加同样会导致星座平面备份卫星数量的增加,因此星座可用度也会上升。然而,不能无限增加,因为当>5时>34,一次发射的火箭数量超过了运载火箭运力的限制。当从3增长至4时带来的边际效应最为明显,即减小单位备份费用可以增加最多的星座可用度。同样,随着的增加星座总备份费用在上升的同时星座可用度也随之上升,这是因为运载火箭一次发射的卫星数量越多,平均每颗卫星的发射费用会大幅降低,因此带来总备份费用的降低。而的增加同样会导致星座停泊轨道备份卫星数量的增加,因此星座可用度也会上升。然而,不能无限增加因为运载火箭运力的限制≤34。当从24增长至28时带来的边际效应最为明显,即减小单位备份费用可以增加最多的星座可用度。

从图6两组数据对比来看,对于星座可用度的影响十分明显,平均增加1个会增加013的星座可用度且减少210百万的备份费用。对于星座备份费用的影响更为显著,平均增加一组可以降低2354百万的备份费用。因此,调整比调整可以为星座配置带来更好的边际效应。

4.3 方法有效性论证

431 三级备份策略与两级备份策略的比较

为了验证星座多级备份策略的可行性和有效性,基于表2的星座参数,只对星座进行传统的在轨备份和地面备份两级备份,在星座可用度指标同样为099下,星座每年的备份费用为67243百万美元。相比之下,引入了停泊轨道的三级备份策略费用为45469百万美元,同比节省3238%。星座两级备份策略的输出结果如表4所示。使用两级备份模式时,最优的备份策略为:每条轨道备份卫星低于2颗卫星时一次性从地面发射28颗卫星进行补充,同时地面贮存85颗备份卫星。

表4 星座两级备份策略优化结果

不同星座规模下三级备份策略相对两级备份策略带来的备份费用的降低情况不同。图7(a)展示了在星座平面数量为40个时,三级备份策略比两级备份策略节省的备份费用比例随每个平面上卫星颗数的变化。随着每个平面上卫星数量的增加,三级备份策略比两级备份策略节省的备份费用的比例越来越少,当每个平面上有100颗卫星时,三级备份策略能节省12.01%的备份费用,而当每个平面上只有10颗卫星时可以节省51.70%的备份费用,这是因为每个平面上卫星数量越少,三级备份策略“一箭多星”带来的发射费用的降低越明显;当每个平面上卫星数量增加时,每个平面上的失效卫星数也在增加,此时两级备份策略会选择一次性发射更多卫星来维持星座可用性,从而降低了发射费用,也因此缩小了与三级备份策略的备份费用差距。图7(b)展示了在星座平面数量为5个时,三级备份策略比两级备份策略节省的备份费用比例随每个平面上卫星颗数的变化。可以看出,当每个星座平面卫星数减小到3颗以下时,两级备份费用比三级备份费用低,这是因为当星座规模减小时,“一箭多星”带来的发射费用降低效果会显著下降,且增加的停泊轨道备份会引入更多数量的备份卫星,从而增加在轨贮存费用,导致两级备份费用反而比三级备份费用低。

图7 不同星座备份策略在每条轨道上卫星数目不同的 情况下的备份费用Fig.7 Backup cost of different constellation backup strategies under the condition of different numbers of satellites in each orbit

图8(a)展示了每个星座平面上有40颗卫星时,三级备份策略比两级备份策略节省的备份费用比例随星座平面数的变化。可以看出,三级备份费用比两级备份费用节省的比例随星座平面数的变化没有明显规律,星座平面数量并没有明显影响到三级备份策略对比传统两级备份策略的费用节省比例。对于给定的星座规模,三级备份费用平均比两级备份费用节省32%。图8(b)展示了每个星座平面上有5颗卫星时,三级备份策略比两级备份策略节省的备份费用比例随星座平面数的变化。可以看出,星座平面数减少到5个以下时,两级备份费用比三级备份费用低,这是因为与图7(b)类似,当星座规模减小时,“一箭多星”带来的发射费用降低效果会显著下降,且增加的停泊轨道备份会引入更多数量的备份卫星,从而增加在轨贮存费用,导致两级备份费用反而比三级备份费用低。

图8 不同星座备份策略在星座平面数不同情况下的 备份费用Fig.8 Backup cost of different constellation backup strategies under the condition of different numbers of constellation plane

可用度指标是星座运营商衡量服务质量的重要方式,也对备份费用起着决定性作用,为了保证更高的性能要求,必将增加备份卫星数目,从而增加备份费用。为了体现三级备份策略比两级备份策略的优越性,对比了不同可用度指标下不同备份策略下星座备份的成本,三级备份策略对比两级备份策略备份费用节省的比例随星座可用度指标的关系如图9所示。无论在何种星座可用度指标下,三级备份策略都比两级备份策略节省大量备份费用,其中在星座可用度指标为0.99时,三级备份策略比两级备份策略节省43%的备份费用;在星座可用度指标为0.8时,三级备份策略比两级备份策略节省73%的备份费用。星座可用度指标越低,三级备份策略会比两级节省的费用越多,这是因为在可用度指标越低时三级备份策略更能利用“一箭多星”发射带来的发射成本的优势,最大化利用火箭运力一次性发射多颗卫星从而降低发射成本。除了使用GA对该优化问题进行求解以外，本文还通过MA法进行求解并对比两种方法在求解此类问题时各自的优缺点。

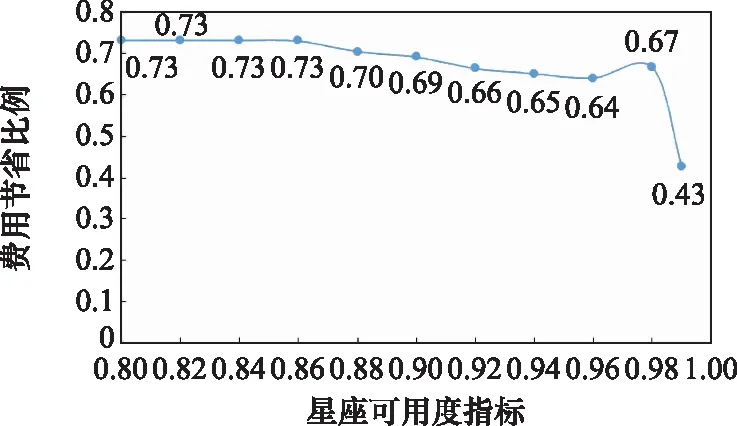
图9 不同星座可用度指标下三级备份策略对比两级备份策略 备份费用节省的比例Fig.9 Percentage of backup cost savings of three-level backup strategy and two-level backup strategy under different constellation availability indicators

4.3.2 GA与MA的比较

MA主要研究一种因素的变化所带来的另一种因素的变化程度,作用在于能够在星座备份成本性态分析的基础上,界定变动成本和固定成本后,明确星座备份策略决策的方向,使得星座运行管理决策有“法”可依,科学有效。而且由于MA属于相关性分析,有助于理清各个相关变量之间变化的规律,使复杂问题简单化,助力目标最优化的决策。使用MA对GA的计算结果进行分析,是因为GA输出的结果并不能得到星座备份策略的边际效应,也就无法研究各个变量对星座可用度及备份费用的影响程度,这对于星座管理者的决策过程十分重要。GA与MA的计算时间如图10所示。

图10 GA与MA的计算时间对比Fig.10 Computation time comparison of GA and MA

显然,在各种星座规模下GA的计算时间比MA都有更大优势,这是因为GA没有计算所有情况下的结果,而是使用特定的搜索方式来寻找最优解。在各种星座规模下,GA的迭代次数最多为148次,计算时间仅3.6 s;而对于相同的优化问题,MA需要计算1.6×10次(具体计算次数与变量的优化范围有关),即使采用八核心处理器并行计算时间最短也需363.2 s,可见采用GA对于计算速度的提升极为明显。

5 结 论

本文研究了一种基于METRIC理论的超大规模卫星星座备份策略模型,同时考虑地面、停泊轨道以及星座平面3种备份模式对卫星星座进行备份,并考虑在轨卫星随机失效的情况下使用(,)库存管理策略对备份卫星进行管理。以星座三级备份可用度为优化约束,以星座备份费用为目标函数,建立起备份策略数学优化模型。模型充分考虑小型卫星批量化生产以及运载火箭“一箭多星”发射,相比传统备份策略大量节省备份费用;模型采用GA进行求解,相比传统优化算法节省大量计算时间。

(1) 本文将METRIC模型应用在超大规模低轨卫星星座中,构建了包含地面备份、停泊轨道备份和星座平面备份的多级备份策略模型,建立了以制造费用和发射费用组成的星座备份费用为优化目标,以地面可用度、停泊轨道可用度和星座平面可用度组成的星座可用度为约束条件的星座三级备份数学优化模型。

(2) 将某超大规模低轨卫星星座作为研究对象,通过GA对所构建的模型进行求解,得到最优的星座备份策略。在星座最优备份配置下,,,与4个变量中改变的值会使可用度随备份费用的变化最明显,即改变的值对于提高星座可用度的效果更好。

(3) 计算表明三级备份策略比传统两级备份策略可以节省32%的备份费用,证明了星座多级备份策略的可行性和有效性。

(4) 与MA相比,GA对于本文复杂非线性混合整数优化问题的求解速度优势十分明显,然而不能分析每个变量的边际效应;MA计算速度远不及智能优化算法,但可以研究每个变量对计算结果的影响程度,这对于决策者十分重要。